机器人导航路径的动态细化分工花授粉算法规划

王志俊

（山西建筑职业技术学院计算机工程系，山西 太原 030006）

1 引言

当前机器人应用领域越来越广泛，包括工农业生产、生活服务、军事领域等，不仅将人类从繁重生产劳动中解放出来，而且可以高效高质量完成生产任务。机器人导航方法决定了机器人工作效率和安全性，包括目标定位、环境建模、路径规划等三个方面[1]，研究的是路径规划这一关键技术，旨在提高机器人行走效率和顺滑性。

根据路径规划方法提出时间，一般将路径规划分为传统方法和智能规划方法，传统规划方法有栅格法、可视图法、拓扑法、人工势场法等[2-3]，智能规划方法有遗传算法、神经网络、混合算法等[4-5]。智能规划方法的效果与环境适应性明显优于传统方法，而传统算法高效的环境建模方法和面对机器的可识别性具有借鉴价值，因此传统规划方法与智能规划方法的结合成为了一个研究方向。文献[6]将蝗虫优化算法与栅格环境法结合，使用Pareto 最优准则给出了路径长度、平滑度、安全性的多目标优化解；文献[7]将遗传算法与人工势场法相结合，使用遗传算法规划静态全局最优路径，使用人工势场法实现动态避障，可以实现动态环境下路径规划。纵观各种智能规划方法，路径性能主要取决于算法性能，但是单一算法皆具有局限性，新算法提出、现有算法性能升级、多算法优势互补融合成了当前的热门研究方向。

研究了机器人在静态环境下的路径规划问题，通过改善现有算法性能达到减小路径长度的目的。以花授粉算法为基础，将花粉划分为精英个体、优等个体、差等个体，精英个体引领算法进化方向，优等个体负值寻优搜索，差等个体通过柯西变异逃出局部最优。使用个体动态细化分工花授粉算法进行路径规划，达到了减少路径长度的目的。

2 个体动态细化分工花授粉算法

2.1 花授粉算法

花朵授粉存在自花授粉和异化授粉两种方式，自花授粉是指花粉成熟后传播到自身植株上，异化授粉是指花粉以蜜蜂等动物携带的方式传播到其他植株上，传播范围较广。模拟花授粉行为，将自花授粉视为局部搜索，将异化授粉视为全局搜索，因而出现了花授粉算法。花授粉算法核心思想为：设置一个转换概率p和随机数 rand∈（0，1），当 rand＞p则进行全局搜索，若 rand≤p则进行局部搜索[8]。

（1）全局搜索。全局搜索模拟Levy飞行方式进行位置更新[9]，方法为：

式中：λ=1.5，Γ（λ）—标准 gamma 函数；s—利用 Mantegna 算法产生的步长，即：

式中：v—N（0，1）；μ—N（0，σ2），方差 σ2的计算方法为：

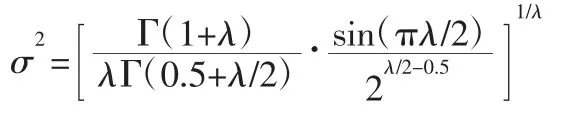
（2）局部搜索。局部搜索以异于自身的两个花粉差分为牵引，即：

（3）贪婪选择。花粉每更新一步，则判断更新前后位置优劣，并根据贪婪准则选择[10]。记f（）为目标函数，目标函数越小则花粉位置越优。当时进行位置更新，否则不进行位置更新。花粉位置更新后进行全局最优判断，若则更新全局最优，否则不更新。

（4）算法结束条件。当所有花粉完成一次迭代时才进入下一轮迭代，当迭代次数达到最大迭代次数Tmax时算法停止，输出全局最优即为花粉最优位置。

通过以上介绍可以看出，花授粉算法依据随机数选择授粉方式，种群内个体位置更新方式完全一致，没有进行细致分工。另外，算法后期多数花粉在全局最优牵引下向其接近，不仅使种群多样性降低，而且位置更新能力极低。为了解决以上问题，使用动态细化分工方法和改进搜索策略进行改进，提出了个体动态细化分工的花授粉算法。

2.2 个体动态细化分工

原始花授粉算法中，仅仅依赖概率分为自花传播和异花传播，单一而固定的位置更新方式容易破坏算法多样性，且难以跳出局部最优。为了解决以上问题，将种群内个体任务进行细致分工。根据目标函数值将花粉划分为精英个体、优等个体和差等个体，精英个体指全局最优解，用于引领进化方向；优等个体指排名靠前的花粉，按照传统方式进行更新搜索；差等个体使用柯西变异负责跳出局部最优。

（1）精英个体引领进化方向。根据式（1），将精英个体代入后有这意味着全局最优解完全失去了进化能力，为了保持全局最优解的进化能力，同时起到引领种群进化的作用，对精英个体更新方法进行改进。实验研究表明，种群进化具有的一定的规律和方向性，连续两次迭代的最优解连线及其延长线上，必有部分点接近下次迭代最优解。由此，精英个体的更新方法为：

（2）差等个体柯西变异跳出局部最优。花授粉算法在迭代后期的进化能力弱，容易陷入局部最优但是没有跳出机制。种群中较差个体的位置更新价值和借鉴价值极小，因此使用柯西变异的方法使差等花粉的目标函数值快速改变，以柯西变异方式产生新的种群最优，产生新的更新中心点，达到跳出局部最优的目的。柯西变异方法为：

式中：C（0，1）—柯西分布。

2.3 优等个体改进的搜索方式

前文中提到，优等个体使用传统搜索方式进行位置更新，但是随着迭代的进行，花粉以当前全局最优解为中心进行聚集，此时式（1）中的值极小，则这意味着随着算法的迭代，粒子的更新能力和进化能力极弱，使花授粉算法陷入局部最优的僵局。为了使算法在迭代过程中保持更新和进化活力，提出了搜索策略动态调整方法：

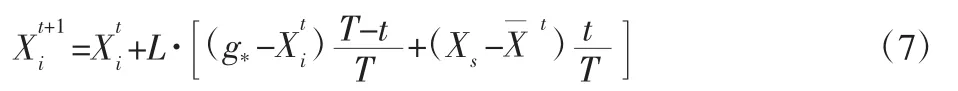
式中：T—最大迭代次数；t—当前迭代次数；Xs—随机选择的异于Xi的花粉，为第t次迭代的位置中心。分析式（7）可知，算法前期主要依赖全局最优进行引导更新，算法后期为了保持更新和进化能力，主要依赖位置中心与个体差分进行引导，使花粉在整个迭代过程中都能够保持进化活力。

2.4 改进花授粉算法流程

将个体动态细化分工和改进搜索方式融入到花授粉算法中，得到个体动态细化分工花授粉算法（Individual Dynamic Refine Division Flower Pollination Algorithm，IDRDFPA）步骤为：

（1）初始化算法参数，包括最大迭代次数T、种群规模Size、转换概率p、花粉移动范围Range；

（2）初始化花粉位置，按照花粉位置的目标函数值进行排序，将花粉区分为精英个体、优等个体、差等个体；

（3）精英个体按式（5）进行位置更新，差等个体按式（6）进行柯西变异；优等个体按式（4）和式（7）进行搜索；位置每更新一次，同时判断是否更新全局最优位置；

（4）判断一次迭代中是否所有花粉完成位置更新，若是则进入（5），否则转至（3）；

（5）判断是否达到最大迭代次数，若否则转至（3）；若是则输出全局最优解，算法结束。

3 路径规划建模及流程

机器人在简单或复杂环境下经过若干次转弯能够达到避障效果，转弯点即为路径结点。基于个体动态细化分工花授粉算法的机器人路径规划思路为：根据环境中障碍物分布确定路径节点数量，使用三次样条插值法确定插值点数量、位置并形成规划路径。花授粉算法的作用是搜索最优的路径结点位置，使规划路径最短。

3.1 三次样条插值法

三次样条插值法使用一系列三次多项式的插值点区间，形成一条平滑的行驶路径，使机器人经过路径结点时具有良好的动力学特性。假设在［a，b］上等距离插入n+1 个点a=x0＜x1＜L＜xn=b，插入点函数值为f（xi）=fi，i=0，1，L，n，三次样条插值函数s（x）需满足三个条件[11]：（1）s（x）在区间［a，b］上二阶连续；（2）s（xi）=fi，i=0，1，L，n；（3）s（x）在每个［xi，xi+1］区间上为三次多项式。则在区间［xi，xi+1］上s（x）表示为：

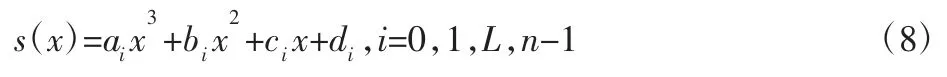
式中：ai、bi、ci、di—多项式系数，s（x）在区间［a，b］上共4n个未知系数，共需4n个确定条件。

3.2 编码方法及目标函数

以每个花粉的编码作为一组路径结点，根据环境中障碍物分布和起点、终点位置确定路径结点数量m，使用改进花授粉算法搜索最优路径结点，由此可知一条路径上m个路径结点横坐标构成了花粉的m维横坐标，路径上m个路径结点纵坐标构成了花粉的m维纵坐标。基于以上分析，将花粉编码为［（xi1，xi2，L，xim），（yi1，yi2，L，yim）］，其中（xim，yim）表示花粉i搜索到的第m个路径结点。

设定的路径规划目标为：在满足避障要求的情况下，规划出最短的行驶路径。目标函数围绕避障和路径最短两个规划目标，构造为：

式中：L—路径长度；P—机器人碰撞标志变量；β—足够大的系数，用于排除发生碰撞的路径，在此取为β=100。路径长度L为：

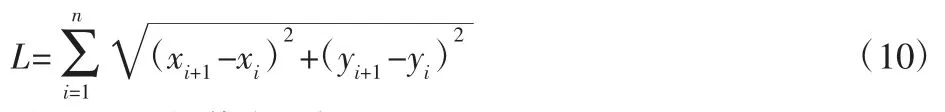
式中：（xi，yi）—插值点坐标。

为了方便进行碰撞判断，将所有障碍物膨胀为圆形，碰撞标志变量P计算方法为：

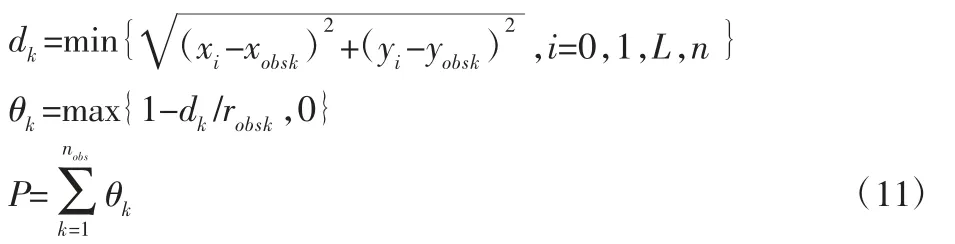
式中：（xobsk，yobsk）—第k个障碍物圆心；（xi，yi）—插值点坐标；dk—插值点与第k个障碍物的距离最小值；robsk—第k个障碍物的半径；θk—轨迹与第k个障碍物的碰撞标志值；nobs—所有障碍物数量。

分析式（11）可知，当存在某一插入点与障碍物中心距离小于障碍物半径时，此时机器人与障碍物发生碰撞，同时θk＞0，则P＞0，结合式（9）在系数 β 的放大作用下，有z＝L（1+βP）＞＞L，此时z值较大，不会成为最优路径。当所有插入点与障碍物不发生碰撞时，θk＝0，P＝0，1+βP＝0，此时z=L，长度最短的无碰路径即为最优路径。

3.3 路径规划流程

结合三次样条插入法原理、改进花授粉算法原理、花粉编码方法及建立的目标函数模型，制定路径规划流程如下：（1）根据路径起点、终点及障碍物分布情况确定路径结点数量m和插入点数量n；初始化改进花授粉算法参数；（2）调用前文给出的改进花授粉算法，分精英花粉、优等花粉和差等花粉分别进行位置更新；（3）根据迭代后的花粉位置和三次样条插值法，确定插值点横纵坐标；根据式（9）计算花粉迭代后位置的目标函数值，依据目标函数值判断是否进行位置更新；（4）若算法迭代次数未达到最大值，则转至（2）继续迭代；若算法达到最大迭代次数，则算法结束，同时输出全局最优路径。

4 仿真验证与分析

分别在简单环境和复杂环境下对个体动态细化分工花授粉算法的规划性能进行验证，同时使用传统花授粉算法（Flower Pollination Algorithm，FPA）、个体动态细化分工花授粉算法（IDRDFPA）、文献[10]的改进蝙蝠算法（UGBA）进行路径规划，仿真运行环境为Windows7，编程环境为Matlab R2014a。为了保证公平公正，算法共有的参数设置为相同值，种群规模Size=30，最大迭代次数T=500，转换概率p=0.8。改进蝙蝠算法的种群规模、最大迭代次数与花授粉算法一致，其余参数与文献[12]保持不变。

4.1 简单环境下规划性能验证

在简单环境下，设置6 个圆形障碍物，根据障碍物、起点和终点分布情况，将路径结点数设置为3，插值点数设置为100。为了防止随机性对实验结果影响，分别使用FPA 算法、IDRDFPA算法、UGBA 算法各自独立运行30 次，取各算法的最优结果进行展示。运行结果，如图1 所示。

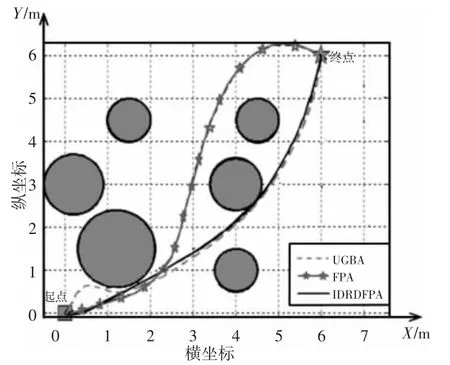
图1 简单环境下各算法搜索的最优路径Fig.1 Optimal Path Searched by Different Algorithm Under Simple Environment

从图1 中可以直观看出，IDRDFPA 算法搜索的路径最短且平滑，而另外两个算法搜索的路径存在明显的曲折部分。算法对最优路径的搜索过程中，目标函数值随迭代过程的变化曲线，如图2 所示。从图中可以看出，提出的IDRDFPA 算法最早搜索到最优路径，迭代次数为82 次；UGBA 和FPA 搜索到最优路径时的迭代次数相差不大，都迭代了200 次左右。从最优路径质量上讲，IDRDFPA 算法规划的路径质量最好，其次为UGBA 算法，FPA 算法规划路径质量最差。为了比较三种算法的性能稳定性，统计30 次独立运行的最优值、最差值和平均值结果，如表1 所示。从表中可以看出，提出的IDRDFPA 算法搜索的路径质量最高，而且稳定性最好。UGBA 算法的最优解质量优于FPA 算法，但是最差解和平均值差于FPA 算法，说明UGBA 算法的稳定性比FPA 算法差。综上所述，在简单环境下，IDRDFPA 算法的最优解质量、算法稳定性和收敛速度均优于另外两种算法。

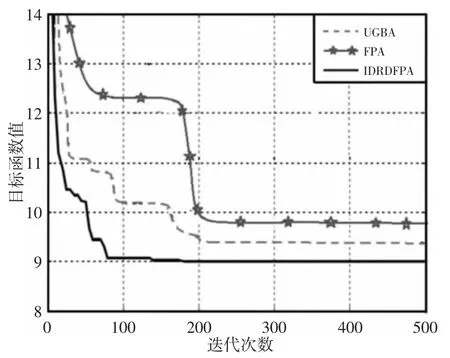
图2 简单环境下各算法迭代过程Fig.2 Iteration Process of Different Algorithm Under Simple Environment

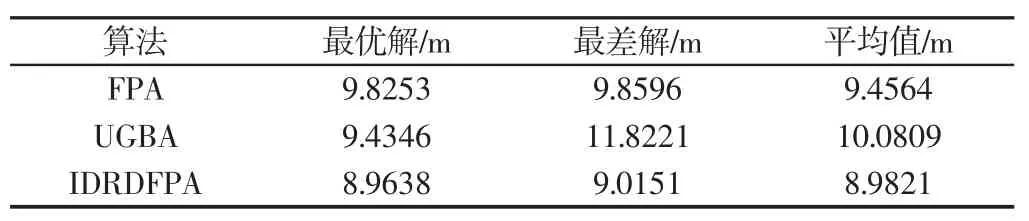
表1 简单环境下各算法搜索的路径统计Tab.1 Path Statistics Searched by Different Algorithm Under Simple Environment

4.2 复杂环境下规划性能验证

在复杂环境下，设置11 个圆形障碍物，根据障碍物、起点和终点分布情况，将路径结点数设置为4，插值点数设置为100。为了防止随机性对实验结果影响，分别使用FPA 算法、IDRDFPA算法、UGBA 算法各自独立运行30 次，取各算法的最优结果进行展示。运行结果，如图3 所示。从图3 中可以直观看出，在复杂环境下IDRDFPA 算法搜索的路径最短，算法对最优路径的搜索过程中，目标函数值随迭代过程的变化曲线与简单环境下相似，这里不再给出。为了比较三种算法在复杂环境中的性能稳定性，统计30 次独立运行的最优值、最差值和平均值结果，如表2 所示。从表2 中可以看出，IDRDFPA 算法搜索的最优路径长度为8.8446，比UGBA 算法和FPA 算法分别减少了5.93%和9.86%。从最优值、最差值和平均值看，IDRDFPA 算法具有最佳的稳定性，其次为FPA 算法，UGBA 算法的稳定性最差。综上所述，在简单环境或者复杂环境下，IDRDFPA 算法具有最好的寻优能力、最快的收敛速度、最佳的稳定性。这是因为对花粉个体的分工进行细化，使精英个体引领进化方向，差等个体通过变异跳出局部最优，优等个体使用改进搜索方式寻优，不同花粉之间协调配合，提高了算法寻优能力、收敛速度和稳定性。

图3 复杂环境下各算法搜索的最优路径Fig.3 Optimal Path Searched by Different Algorithm Under Complex Environment

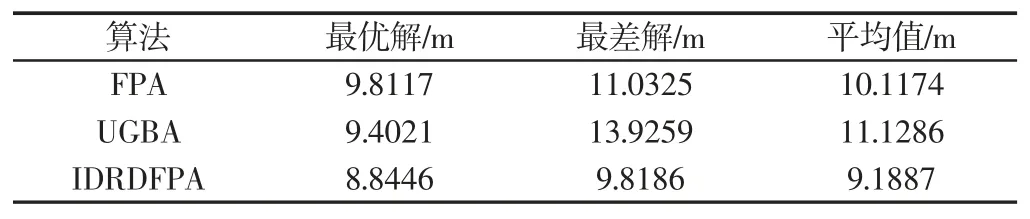
表2 复杂环境下各算法搜索的路径统计Tab.2 Path Statistics Searched by Different Algorithm Under Complex Environment

5 结论

研究了机器人在静态环境中点对点的路径规划问题，提出了个体动态细化分工花授粉算法，使用改进花授粉算法搜索最优路径结点，而后使用三次样条插值法规划出最优路径。经仿真得出以下结论：（1）差等个体的柯西变异可以使算法有效跳出局部最优；（2）优等个体改进的搜索方式可以保持算法长期的更新能力和进化能力；（3）与花授粉算法相比，个体动态细化分工花授粉算法具有最好的寻优能力、收敛速度和稳定性。