移动机器人全覆盖路径规划算法研究

贺利乐，刘小罗，黄天柱，杨剑乐

（1.西安建筑科技大学机电工程学院，陕西 西安 710055；2.中建建乐实业有限公司，陕西 西安 710000）

1 引言

路径规划是移动机器人实现智能化的关键技术之一，分为点对点路径规划和全覆盖路径规划。通常所提的路径规划即点对点路径规划是指，机器人在无碰撞条件下，从起点出发规划出一条到达终点的最短路径，算法首要评价指标为路径长度。但是某些作业要求并不适于点对点路径规划，如：室内清扫机器人、擦窗机器人、草坪修剪机器人等。这些移动机器人路径规划即全覆盖路径规划，不仅要求寻找一条从起始位置到终点的无碰撞最短路径，更重要的是要扫描遍历整个无障碍工作区域，最终形成一条在工作区域内从起始位置经过所有无障碍区域的连续路径[1]，算法首要评价指标为面积覆盖率。全覆盖和点对点路径规划最大的区别在于是否需要遍历整个工作区域。

文献[2-3]提出基于生物激励神经网络构建环境模型，并根据神经元活性值大小决定机器人运动方向，该算法实时性好，能够解决动、静态环境下机器人全覆盖路径规划问题。但存在神经网络环境建模需要机器人每移动一个神经元位置环境模型需更新一次，当神经元数量多时，计算量太大、算法运行效率不高的问题。文献[4]利用单元分解法将环境地图划分为不同大小的区域，区域内部采用螺旋收缩算法实现遍历，区域之间通过图的深度优先搜索算法实现全局遍历排序，最终达到全覆盖路径规划的目的，但此方法易产生小分区，同时由于图的深度优先搜索算法固有缺陷，机器人在实现路径全覆盖时轨迹重复率不高。文献[5-6]基于动态栅格法的环境建模，分别提出优先级A*算法和置信度方向函数实现全覆盖路径规划，但它们只是单一考虑未覆盖区域或者机器人转向，同时当机器人从死区逃离时通常不是最优路径。

针对上述所提算法的不足，这里在构建动态栅格地图的基础上，综合考虑栅格属性、机器人转向、临近栅格距离、未覆盖区域面积大小和逃离死区最优路径，提出一种基于改进的优先级蚁群算法的移动机器人全覆盖路径规划策略，以期达到降低路经重复率，减少转弯次数，提高工作效率。

2 环境建模

环境建模是移动机器人全遍历路径规划的前提和基础，常用的环境建模方法主要有：栅格法、单元分解法、拓扑图法、MAKLINK 图论法[7-8]、神经网络等。这里是在沿边学习的基础上，采用栅格法进行二维环境建模，方法具有简单可靠，易于实现和维护的优点。

2.1 沿边学习

沿边学习是移动机器人沿环境边界或紧靠环境边界的障碍物分别进行水平和垂直运动，通过机器人本体左右侧的测距传感器检测环境或障碍物边界与机器人的相对距离，实现对工作环境轮廓学习的过程，为后期栅格法环境建模奠定基础。对于复杂环境，移动机器人可能需要穿越环境内部，才能达到完全学习整个工作环境轮廓的目的。

2.2 动态栅格法的环境建模

经过环境轮廓学习获得环境地图后，以固定大小将其划分成若干栅格[9]。栅格根据是否含障碍和是否被覆盖，分为障碍栅格、已覆盖栅格和未覆盖栅格。为了便于信息存储和计算处理，每个栅格状态由（x，y，f）描述，（x，y）表示栅格在地图中的位置，f为栅格的属性值，根据式（1）给每个栅格置属性值f。

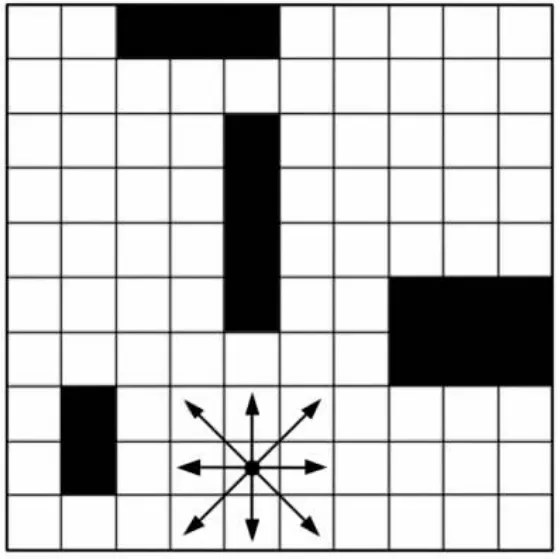
图1 栅格地图Fig.1 Grid Map

动态栅格是指栅格的属性值f是变化的。比如，为增加未覆盖栅格对机器人的“吸引”，避免机器人反复擦拭同一栅格，约定栅格每被覆盖一次，其属性值递减-1。同时，机器人在工作过程中，只更新其已覆盖过栅格的属性值，而不需要类似基于生物激励的神经网络环境模型根据分流方程[2]对所有神经元或者栅格进行迭代计算，极大地减少了计算量，提高了机器人的工作效率。假设机器人栅格地图，如图1 所示。

为便于研究和仿真实验，作如下假设：

（1）机器人在运动过程中，障碍物和环境始终保持不变，即机器人是在静态环境下工作，且障碍物为规则形状。

（2）环境和障碍物边界已根据机器人的实际物理尺寸进行“膨化”处理，故障碍物边界为安全区域且机器人以质点表示。同时，在不存在障碍物和环境边界时，机器人可向邻域8 个方向的栅格运动，如图1 所示。

（3）机器人覆盖一个栅格后即认为其已按要求完成工作，比如清扫或者擦拭工作。当再次覆盖同一栅格时，属于重复遍历。

3 全覆盖路径规划算法

基于环境模型机器人根据既定优先级规则不断选择拟移动栅格，当机器人陷入死区时，采用逃逸算法规划出迅速逃离死区的路径，并继续既定任务，最终达到全覆盖的目的。在动态栅格法环境建模基础上，优先级规则和逃逸算法直接关系到机器人的面积覆盖率和轨迹重复率，是全覆盖路径规划研究的重点。

3.1 改进的优先级启发规则

文献[5]所提算法将启发式规则定义为上栅格、下栅格、左栅格优先次序，规则简单可行，但机器人频繁转弯，能耗较大。文献[6]所提算法考虑机器人转向，利用方向函数策略使得规划路径尽可能保持直行，减少能耗，但这类似于机器人随机运动方法，机器人易陷入死锁状态。

针对传统算法中存在的问题，在考虑栅格属性和机器人转向的基础上，引入邻域栅格距离项和未覆盖区域面积大小项，提出如式（2）优先级启发规则，供机器人在非死区状态下选择下一移动栅格位置。

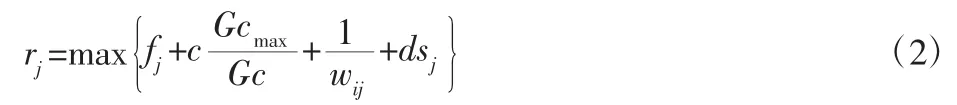
式中：fj—栅格j的属性值，栅格j属于机器人当前栅格i的邻域栅格。Gcmax—机器人在当前栅格时未覆盖的栅格总数；Gc—拟移动栅格方向一侧未覆盖栅格数量与原运动方向上的未覆盖栅格数量之和。当拟移动栅格的方向与原方向一致时，如果除移动方向外不存在未覆盖栅格，则规定如果只有一侧存在未覆盖栅格，Gc为该侧所求Gc减0.5；如果两侧均存在未覆盖栅格，Gc为最少一侧所求Gc加0.5。该项的设置是确保机器人先遍历未覆盖栅格数量最少一侧后转而遍历另一侧，以期降低机器人的路径重复率。wij—当前栅格i与拟移动栅格j之间的距离。当拟移动栅格在当前栅格的整数倍方向时取wij＝1.414；当拟移动栅格在当前栅格的整数倍方向时取wij＝1。sj—转向函数是关于机器人前一栅格rp、当前栅格rc与拟移动栅格rj之间方向角差值△θj的函数。下式为机器人方向角差值△θj。

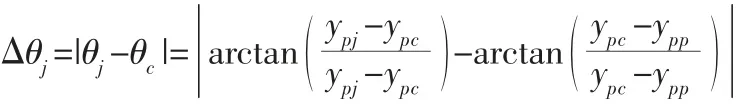
式中：（xpp，ypp）、（xpc，ypc）和（xpj，ypj）—前一栅格rp、当前栅格rc与拟移动栅格rj的位置坐标，方向角计算简图，如图2 所示。θj—拟移动栅格rj和当前栅格rc的角度差。θc—当前栅格rc和前一栅格rp的角度差。△θj∈［0，π］，由于每次只能运动到当前栅格的邻域，所以△θj常取

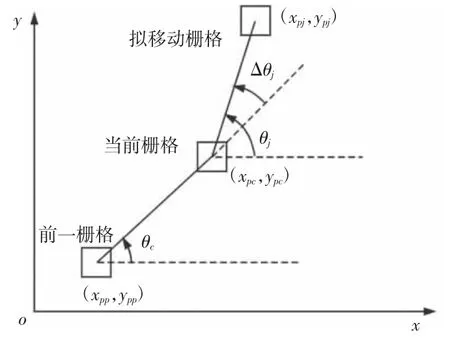
图2 方向角计算简图Fig.2 Simplified Diagram for Calculating the Direction Angle

c为未覆盖区域系数，表示原运动方向两侧中未覆盖栅格数量最少一侧对机器人选择下一栅格的影响程度，取c=0.5。

d为转向系数，表示转向对机器人选择下一栅格的影响程度，取d=0.5。

当机器人处于非死区状态时，根据式（2）求出机器人邻域栅格中该项最大者作为下一步实际移动位置，然后重复此过程，直至机器人陷入死区。

3.2 机器人逃离死区

对于全覆盖工作要求而言，机器人在动态栅格法构建的环境地图里面运动过程中常常会陷入死区。机器人陷入死区是指它的周边相邻栅格是边界、障碍物栅格和已覆盖栅格的组合，不存在未覆盖的栅格，只有从死区逃离出来，才能继续全覆盖任务。而逃离死区的路径，影响全覆盖的路径重复率[6]。当机器人利用优先级启发规则陷入死区时，采用蚁群算法能够快速规划出最优逃离路径，很好地解决了此问题。

3.2.1 搜索临时目标点

当机器人陷入死区时，在利用蚁群算法逃离死区之前，必须确立一个临时搜索点，作为机器人逃离目标点，它要求栅格未被覆盖且距机器人当前位置距离最短。同时，目标点的选取影响机器人的重复率的高低。在充分考虑障碍物的基础上，选取离机器人实际距离最近的点作为临时目标点，从而极大降低了重复率。

假设机器人当前位置为Pr（xc，yc），待选栅格位置为Pi（xi，yi），i=1，…，m，m为满足条件的待选目标点的总数。当机器人与待选点之间不存在障碍物时，机器人位置与待选栅格之间的距离di，如式（3）所示。

当机器人与待选点之前存在障碍物时，可将障碍物位置描述为Qri=｛A（x1i，y1i），B（x1i，y2i），C（x2i，y1i），D（x2i，y2i）｝。首先将距离机器人当前位置最近且到直线PrPi垂直距离最短的障碍物顶点作为过渡点，比存在障碍物时点B即为过渡点，如图3 所示。然后根据式（4）求距离di。

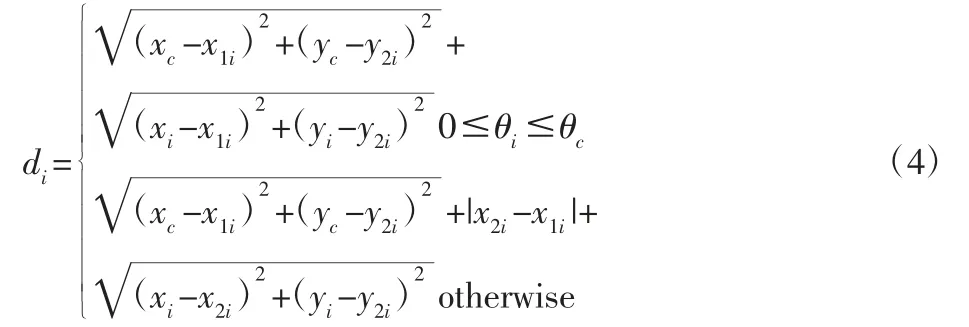
式中：θc—机器人当前位置、过渡点和坐标轴之间的夹角；θi—待选栅格、过渡点和坐标轴之间的夹角。

图3 存在障碍物时机器人位置与待选栅格距离Fig.3 The Distance Between the Robot Position and the Grid to be Selected in the Presence of Obstacles

在求得所有待选栅格与机器人位置距离di后，比较得到di距离最小栅格并记其位置坐标为po（xo，yo），此栅格即作为机器人逃离死区时的临时搜索点。

3.2.2 蚁群算法

当确定临时搜索点后，机器人逃离死区的过程转化为点对点路径规划问题。文章采用蚁群算法能够快速规划出最优逃离路径，较好地解决了此问题。

蚁群算法是在模拟自然界蚂蚁群体觅食行为的基础上提出的智能优化算法，具有全局寻优能力强和复杂程度低等特点。传统的蚁群算法中，蚂蚁k在t时刻由位置i选择下一位置j时，倾向于选择短路径且信息素浓度高的作为移动方向，忽略了路径规划全局寻优性的要求，为此在状态转移规则中引入能表征拟移动位置与目标位置距离项，使搜索更具导向性。蚂蚁在状态转移时首先产生一个随机数0≤q≤1，如果q≤q0则按照状态转移规则式（5）选取下一位置，否则按照转盘赌式（6）选择。

式中：S—按照转盘赌式（6）选择的下一位置。

式中：j∈allowedk—蚂蚁k下一步允许转移的位置；τij—边（i，j）上的信息素浓度；ηij—一个启发信息，通常γjg—允许转移位置到目标位置之间的欧式距离；α、β、γ—信息素浓度、启发信息和目标位置信息在蚂蚁选择路径中的相对重要程度。

对于信息素更新而言，为有效避免蚂蚁收敛到同一路径，蚂蚁从城市i向城市j移动时需要局部信息素更新，规则如式（7）所示。

式中：μ—信息素挥发系数，0＜μ＜1；τ0—一小正常数。

在所有蚂蚁完成一次迭代后进行全局信息素更新，根据最大最小蚂蚁系统原理，只增强当前迭代最优路径上的信息素[10]，同时为避免出现停滞现象，每次迭代信息素浓度设置上下限τmin≤τij（t）≤τmax。全局信息素更新规则，如式（8）所示。

式中：ρ—信息素挥发系数，0＜ρ＜1；Lib—当前迭代最优路径。

3.3 改进算法具体步骤

改进优先级蚁群算法移动流程图，如图4 所示。

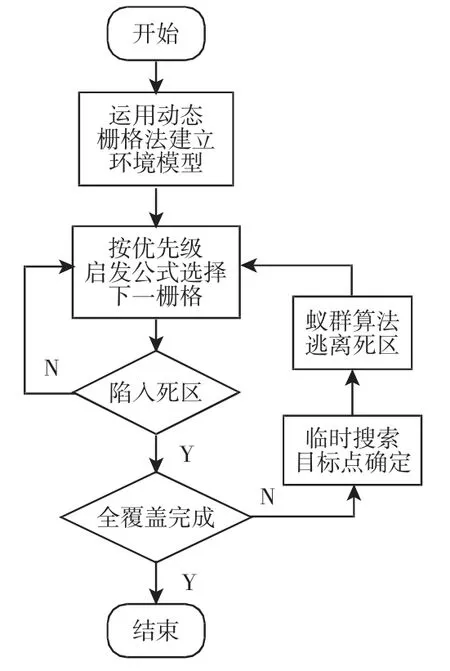
图4 改进优先级蚁群算法流程图Fig.4 The Flow Chart of Improved Priority Rule with Ant Colony Algorithm

具体步骤描述如下：

（1）环境建模。利用机器人本体上的传感器对环境进行沿边学习得到环境轮廓，对其进行等大小网格划分，并根据各网格的状态置属性值，最终形成栅格地图。

（2）路径选择。机器人根据改进的优先级规则式（2）寻找下一可行栅格，并修改已覆盖栅格的属性值，如此循环直到机器人当前位置邻域栅格不存在未覆盖栅格。

（3）陷入死区。遍历栅格地图，如果存在属性值为1 的栅格，则转（4）；否则转（6）。

（4）临时目标点。当机器人与待选点之间不存在障碍物时，根据式（3）求它们之间的距离；当机器人与待选点之前存在障碍物时，根据式（4）求它们之间的距离；最终选择距离最短栅格作为临时搜索目标点。

（5）逃离死区。蚁群算法状态转移规则加入距离目标点项，然后机器人利用其规划出最优逃离死区路线，并转步骤2 继续进行路径全覆盖工作。

（6）结束搜索。当栅格地图中不存在属性值为1 的栅格时，表示全覆盖工作已经完成，算法结束。

4 仿真验证

4.1 路径规划算法性能指标

机器人全覆盖路径规划算法常用性能评价指标为转弯总数、轨迹重复率和面积覆盖率。令SΩ表示机器人待覆盖区域总面积，Sd表示机器人已覆盖（单次）区域总面积，Sg表示机器人完成全覆盖任务后经过区域总面积，T表示机器人转弯总次数。

转弯总次数T是指机器人运动方向改变45°的次数。

面积覆盖率pc是指机器人完成任务后单次覆盖区域总面积Sd与机器人待覆盖区域总面积SΩ的比值：

轨迹重复率pr是指机器人多次覆盖的区域面积Sg-Sd与待覆盖区域总面积SΩ的比值：

综合机器人运动过程的转弯数、面积覆盖率和轨迹重复率等指标全面评价全覆盖路径规划算法。若转弯总数越低、面积覆盖率越高、轨迹重复率越低，则机器人工作效率越高，路径规划算法可行越好。

4.2 仿真分析

为说明所提算法的可行性和有效性，在10*10 的环境地图下，分别采用文献[5-6]和所提算法进行全覆盖路径规划仿真实验。不同算法全覆盖路径规划仿真结果，如图5 所示。其中标识点S表示机器人的初始位置，标识点F表示机器人的终止位置。文献[5]基于优先级A*算法的路径规划仿真结果，如图5（a）所示。文献[6]基于方向信度函数算法的路径规划仿真结果，如图5（b）所示。所提算法的路径规划算法，如图5（c）所示。不同路径规划算法性能指标，如表1 所示。

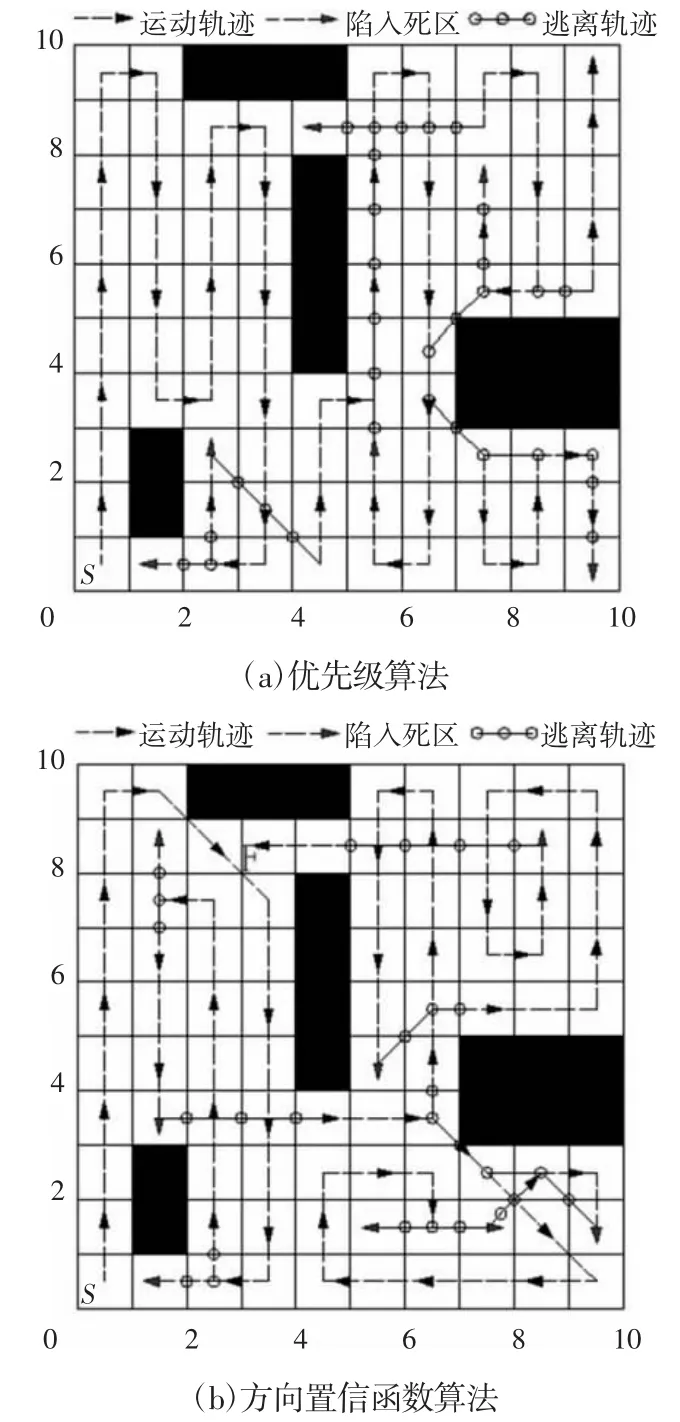
图5 不同算法全覆盖路径规划仿真结果Fig.5 The Simulation Results of Different Complete-Coverage Path Planning Algorithms

表1 不同算法性能对比Tab.1 Performances of Different Algorithms

通过图5 和表1 可知，虽然不同算法均可实现面积全覆盖，但机器人的转弯次数和轨迹重复率不尽相同。文献[5]的路径规划算法由于强调环境地图的左侧始终保持已覆盖状态，使转弯总数和轨迹重复率较高；文献[6]的路径规划算法利用方向信度函数尽可能使机器人保持直线运动以降低能耗；使转弯总数和轨迹重复率较文献[5]所下降；综合考虑机器人转弯能耗和未覆盖区域的基础上，提出新的优先级启发规则，同时当机器人陷入死区时，利用蚁群算法能够找到最优路径。比较文献[5-6]，本算法不仅陷入死锁次数较少，而且在轨迹重复方面分别降低了81.80%和66.64%；在转弯总数方面，本算法比文献[5]降低了26.83%，而与文献[6]相差不大。仿真实验结果表明，所提算法在保证面积全覆盖的基础上，更加有效地降低了轨迹重复率，减少了转弯次数，提高了机器人工作效率，降低了能耗。

5 结论

针对常见移动机器人全覆盖路径规划算法的不足，提出一种改进优先级蚁群算法。该算法在传统优先级启发规则的基础上进行了改进，在机器人状态陷入死区时，进一步考虑了死区点到临时搜索点之间存在障碍的情况。通过仿真实验表明，改进后的方法在保证面积覆盖率为100%的同时能降低死锁次数和轨迹重复率，方法可行有效，为移动机器人全覆盖路径规划提供了参考。