VMD 能量熵与随机森林相结合的齿轮故障诊断

周旺平，王 蓉，许沈榕，宋晓莉

（1.南京信息工程大学自动化学院，江苏 南京 210044；2.中国科学院国家天文台南京天文光学技术研究所，江苏 南京 210042）

1 引言

齿轮作为机械配置中基础的传动元件，在工业设备中具有普遍应用[1]。检测齿轮运行状态，识别齿轮故障类型，对故障齿轮进行及时更换或修复，可以预防事故突发情况，降低设备维修成本。

当齿轮出现点蚀、裂纹、剥落、磨损等情况时，其振动信号表现出非线性、非平稳性等特征[2]。针对此类信号，传统的时域分析或频域分析很难准确提取到齿轮的故障频率。文献[3]利用经验模态分解（EMD）将振动信号分解成有限个平稳的固有模态函数，分离出噪声和背景信号，验证了EMD 可以提取齿轮故障特征；文献[4]针对EMD 抗模态混叠效果差，提出EEMD 和Teager-Huang 变换结合的齿轮故障诊断方法；文献[5]提出一种新的自适应信号分解方法—变分模态分解，将信号以非递归、变分模态方式进行分解，具备一定的理论基础；文献[6]将VMD 应用到齿轮状态监测中，结论证明该方法对于故障特征提取具有较高的识别度；文献[7]对比分析了EEMD 与VMD 的分解结果，VMD 可以分离频率相近的谐波，具有较好的鲁棒性，避免模态混叠现象。

目前，应用于齿轮箱故障识别的人工智能算法主要为支持向量机。SVM 在处理小样本、非线性等问题展现出良好的效果，多应用于故障诊断领域[8]，但SVM 的参数寻优难，针对多分类问题时，学习能力弱，准确率低[9]。齿轮不同状态下对应的特征值往往具有多样性，导致同一种特征值在不同状态下的诊断效果不是最优，为此需要提取多种特征。随机森林作为集成学习中的一种经典算法，利用多棵决策树对样本进行训练并预测，可以集成多种特征向量，有效提高故障分类的准确率[10]。此外，随机森林调参简单，默认参数下，也可以较好的对样本进行训练与分类。

鉴于VMD 与随机森林的优点，提出了一种VMD 和随机森林相结合的故障识别的方法。采用VMD 分解对齿轮振动信号进行处理，得到有限个模态分量，计算其能量熵，构建高维特征向量输入到随机森林分类器中，对齿轮进行分类故障识别，并与传统的故障识别方法相对比。

2 变分模态分解

VMD 是2014 年提出来的一种非递归、自适应的信号处理方法，它的主要核心是构造变分问题和求解变分问题，由经典维纳滤波、频率混合、希尔伯特变换为基础来求解。VMD 可以将多组分信号非线性地分解成具有特定稀疏性的IMF 集合[11]。

2.1 构造变分问题

VMD 将实际信号f分解成K个离散的IMF 分量，使所有分量的带宽之和最小。

（1）对分解的模态函数进行Hilbert 变换，得出与各个模态相关的解析信号与其单边谱；

（2）预估解析信号的中心频率，加入指数项进行调整，将频谱调制到对应的基频带上；

（3）根据解调信号的高斯平滑度来估算带宽，计算梯度L2的范数。

受约束的变分问题表示为：

式中：×—卷积；f—实际信号；uk—模态函数；ωk—各模态对应的中心频率。

2.2 求解变分问题

引入二次惩罚项α 和拉格朗日因子λ，把受约束的变分问题转换为无约束的变分问题，再对其进行求解。定义增广拉格朗日乘数，表示为：

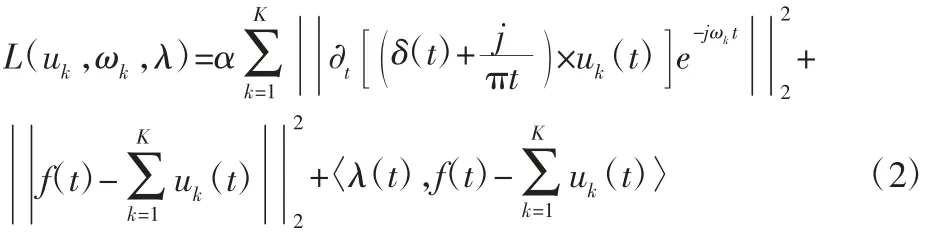
根据交替方向乘子法（ADMM）解决无约束变分问题，轮换更新求得鞍点。

根据parseval 定理，转换到频域的表达式为：

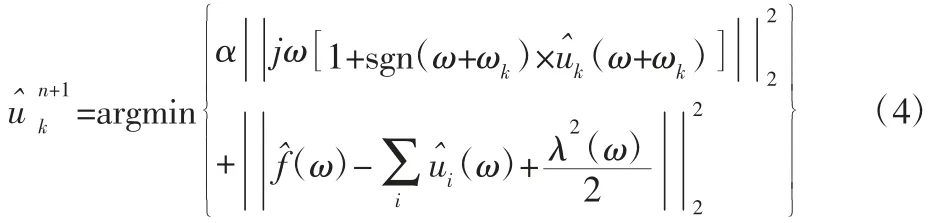
利用ω=ω-ωk进行变量代换，最终得到：

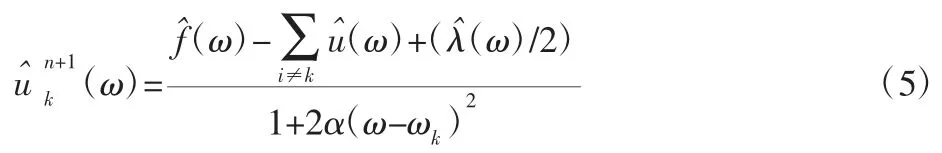
3 VMD 能量熵

VMD 分解得到的模态分量中包含了不同频段的信息。当齿轮产生不同类型的故障时，不同频段的分量将发生改变，同时导致分量瞬时能量随之变化[12]。计算各模态分量的能量熵，从而表示各分量的改变，能够很好地反映出信号在不同尺度的故障特征。

原始信号f经过VMD 分解处理后得到有限个模态分量，每个模态分量依次表示为E1，E2，…，EK。各分量包含了不同频段的振动信息，故总能量E=E1+E2+…+EK，构成振动信号在不同频域的能量分布。因此，VMD 能量熵定义为：

4 随机森林分类算法

随机森林是Leo Breiman 提出的一种综合多棵决策树的分类器，基本原理是利用多棵树对样本进行训练并预测，其中每棵树所使用的数据为随机子集，分类测试相互独立[13]。单个决策树的分类能力较弱，随机森林即随机产生多棵决策树，对每棵树的分类结果进行统计投票，选择最可能的分类结果，分类精度高且避免过拟合问题。随机森林属于有监督的机器学习算法，具体执行过程如下：

（1）采用Bootstrap 方法从原始数据集中进行有放回地采样替换，随机生成k个训练样本集，即生成k棵决策树；

（2）假设生成的训练集对应的决策树中有m个属性，在每个节点处从m个属性中随机选n个属性（n＜＜m），从中选择最优属性作为节点的分类属性进行生长；

（3）不限制每棵决策树的生长，不做任何修剪；

（4）利用多个决策树构成的随机森林对新的数据集进行识别与分类，采用投票方式，最终结果以票数多的为准。

5 基于VMD 能量熵和随机森林的诊断

齿轮在正常、点蚀、断齿、磨损四种状态下，VMD 分解的模态分量的能量熵值不同，故把VMD 能量熵作为特征向量，输入至随机森林分类器进行训练与预测。工作流程图，如图1 所示。

图1 流程图Fig.1 Flow Chart

具体步骤如下：

（1）在相同采样频率以及采样点数的情况下，对正常、断齿、点蚀、磨损4 种状态下的齿轮进行数据采集；

（2）对原始信号进行VMD 处理，得到有限个IMF 分量；

（3）计算各IMF 的能量，构建能量特征向量：

由于能量数值大，不方便计算，故对其进行归一化处理，得到：

（4）将特征向量T′输入至随机森林分类器中，进行训练，并预测分类，计算故障识别的准确率。

6 仿真分析

为了检测VMD 算法的有效性，将该方法与EEMD 分解方法进行对比分析。

模拟齿轮仿真信号进行试验：

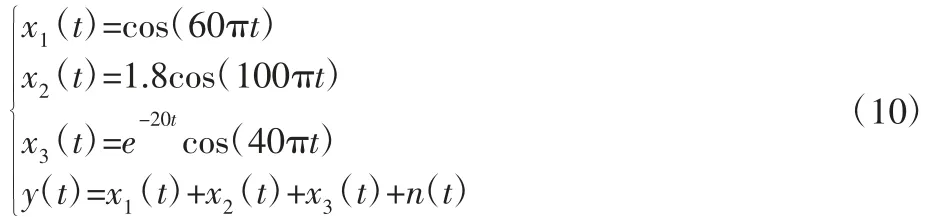
x1（t）与x2（t）为谐波信号，谐波频率为30Hz 和50Hz；x3（t）为周期性衰减信号，其频率为20Hz；n（t）为标准差为1 的高斯白噪声信号；设置采样频率为1000Hz，采样时间是1s，得到信号y（t）的时域波形及频谱，如图2 所示。

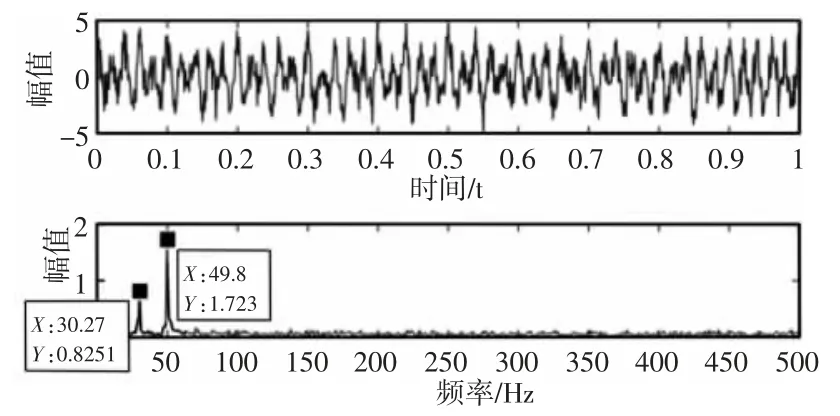
图2 仿真信号及频谱Fig.2 Simulation Signal and Spectrum

该实验对仿真信号进行处理，主要为了提取信号中的脉冲频率20Hz，抑制频率为30Hz 和50Hz 的谐波信号，滤除高斯白噪声，提高主频幅值。VMD、EEMD 分解结果（取EEMD 分解的前三个分量）分别，如图3～图4 所示。EEMD 分解时受到高斯白噪声的影响，产生了模态混叠以及端点效应。EEMD 处理后的包络谱图，如图5 所示。冲击频率20Hz 及其二倍频被提取得到，但同时出现大量的白噪声。仿真信号经过VMD 与包络谱分析后，可以清晰地提取到脉冲频率及其2 倍频、3 倍频，抑制频率30Hz 和50Hz 以及高斯白噪声，如图6 所示。通过对比发现，图5 中出现冲击频率20Hz 的幅值为0.4538，且周围存在较多噪声，图6 中冲击频率的1 倍频幅值为0.6105，且2 倍频、3 倍频的幅值也较为明显，噪声被有效抑制。故相比较EEMD 方法，VMD 分解有效地抑制了谐波信号与噪声，提高了脉冲频率的幅值，提取出脉冲频率的2 倍频、3 倍频，没有出现混叠现象。

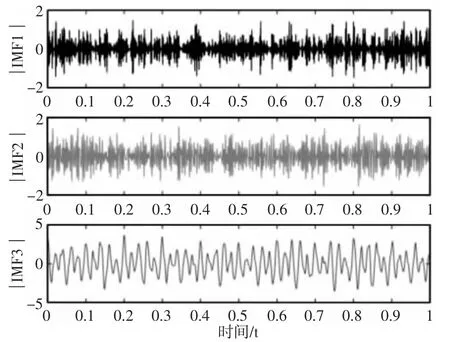
图3 VMD 分解结果Fig.3 Results of VMD Decomposition

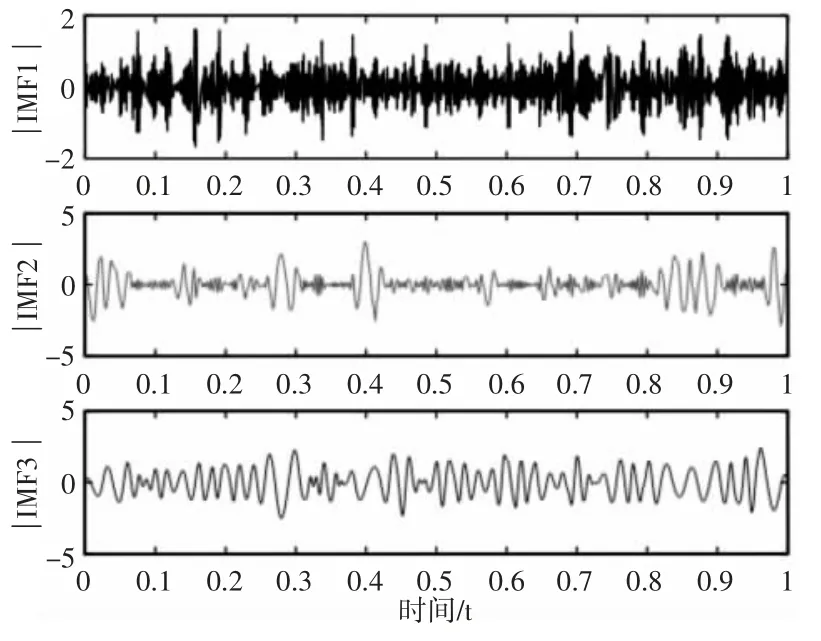
图4 EEMD 分解结果Fig.4 Results of EEMD Decomposition

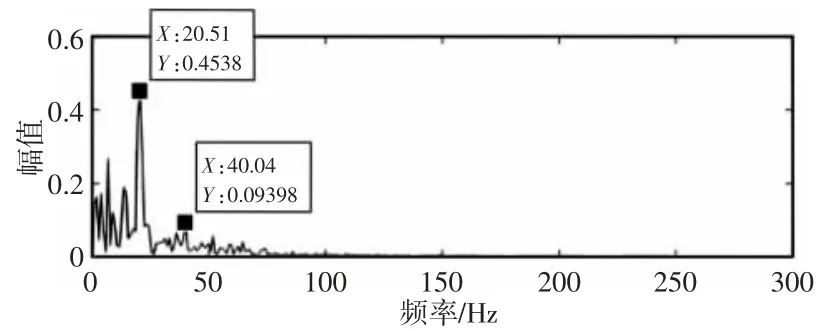
图5 EEMD 处理后包络谱Fig.5 The Envelope Processing by EMD

图6 VMD 处理后包络谱Fig.6 The Envelope Processing by VMD

7 实例分析

选择VB500 机械故障模拟与转子试验台作为实验平台，如图7 所示。

图7 实验台结构图Fig.7 The Structure of Test Bench

该实验台中大齿轮齿数75，小齿轮齿数55，采样频率为5120Hz。实验数据通过NI 9233 采集卡和AC102-1A 加速度传感器采集得到。选择转速为1500r/min，采集齿轮正常、断齿、点蚀、磨损四种状态下的振动信号。以断齿故障为例，采样点数为5120，故障频率为25Hz，时域波形以及频谱图，如图8 所示。本研究采用VMD 算法和EEMD 算法对故障信号进行分解，通过对大量齿轮数据测试，默认VMD 分解的模态分量个数为5，避免信号丢失或过度分解的问题，各模态分量的频谱，如图9 所示。采用EEMD 对振动信号进行处理，共获得13 个IMF 分量，能量主要集中在前几个分量，为方便与VMD 分解对比，故选取EEMD 分解中的前五个IMF 做频谱分析，如图10 所示。对比图9 和图10，EEMD 分解的IMF1 中出现模态混叠现象，难以区分每个成分的个体贡献；因此，模态分量缺乏实际物理意义，受IMF1 影响，IMF2～IMF5 都被扭曲。而VMD 方法能够实现振动信号中自适应分解，有效避免EEMD 分解过程中出现的模态混叠现象，各IMF分量集中在中心频率附近，避免能量泄漏。同时，为了验证各模态分量携带故障信息的有效性，VMD 以及EEMD 分解后各模态的细化包络谱图，如图11、图12 所示。VMD 处理后IMF1～IMF5 的细化包络谱能够清晰地看到故障频率25Hz 及其2 倍频50Hz、3倍频75Hz，EEMD 处理后的细化包络谱中仅有IMF1 能得到故障频率及其倍频，IMF2～IMF4 皆只能观察到1 倍频，IMF5 已看不到明显的故障特征，说明VMD 分解提取的故障信息更为准确。

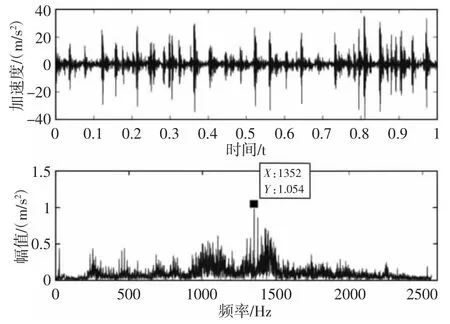
图8 时域波形图及频谱Fig.8 Time Domain Waveform and Spectrum

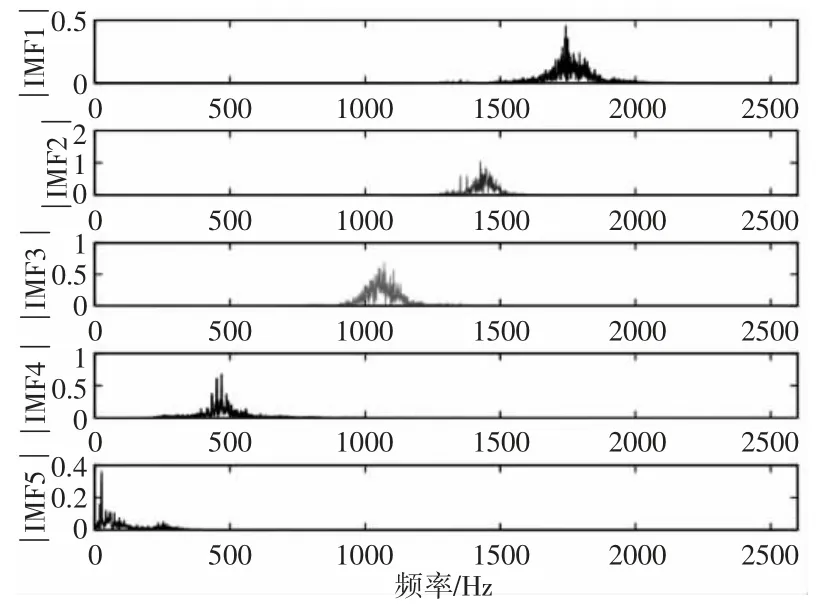
图9 VMD 分解的频谱Fig.9 Spectrum of VMD Decomposition

图10 EEMD 分解的频谱Fig.10 Spectrum of EEMD Decomposition

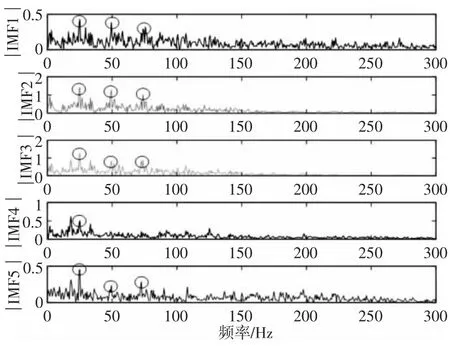
图11 VMD 分解的包络谱Fig.11 The Envelope Processing by VMD

图12 EEMD 分解的包络谱Fig.12 The Envelope Processing by EEMD

分别采集上述4 种状态的信号各100 组，每组信号采样点数为2560，利用VMD 对每组信号进行分解，计算各模态分量的能量熵。每组数据的5 个能量熵组成一组特征向量，每种状态产生 100 组特征向量，构成一个（200×5）的特征向量集，如表 1 所示。每种状态下随机选择50 组特征向量输入随机森林进行训练，剩余50 个特征向量用于测试。在随机森林的训练与测试过程中，数字标签1～4 分别对应着齿轮正常、断齿、点蚀、磨损4 种状态。测试样本存放顺序为：1～50 为正常状态（标签 1）；51～100 为断齿故障（标签 2）；101～150 为点蚀故障（标签 3）；151～200 为磨损故障（标签4）。

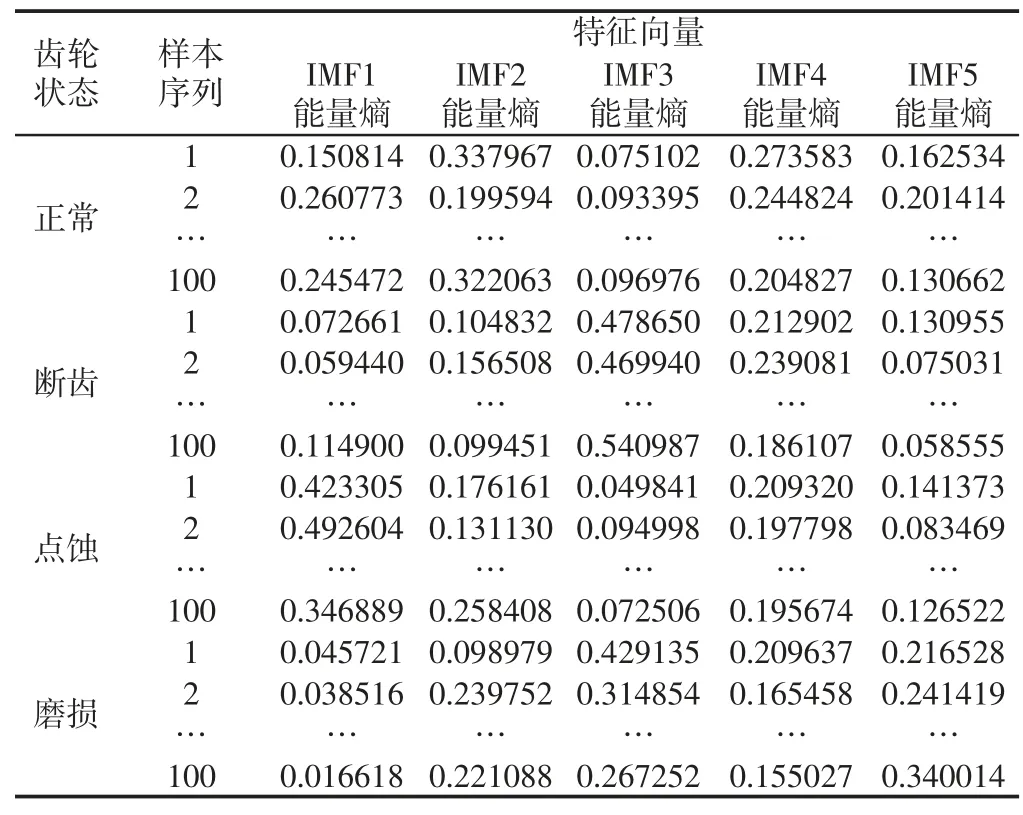
表1 特征向量集Tab.1 Feature Vector Set

袋外数据OBB 误差率收敛曲线，随着决策树个数的增多，误差逐渐减小，当随机森林中决策树的个数为200 时，误差率稳定在0.05 附近，因此分类器中决策树的数量取200，保证样本数据的正确率稳定。

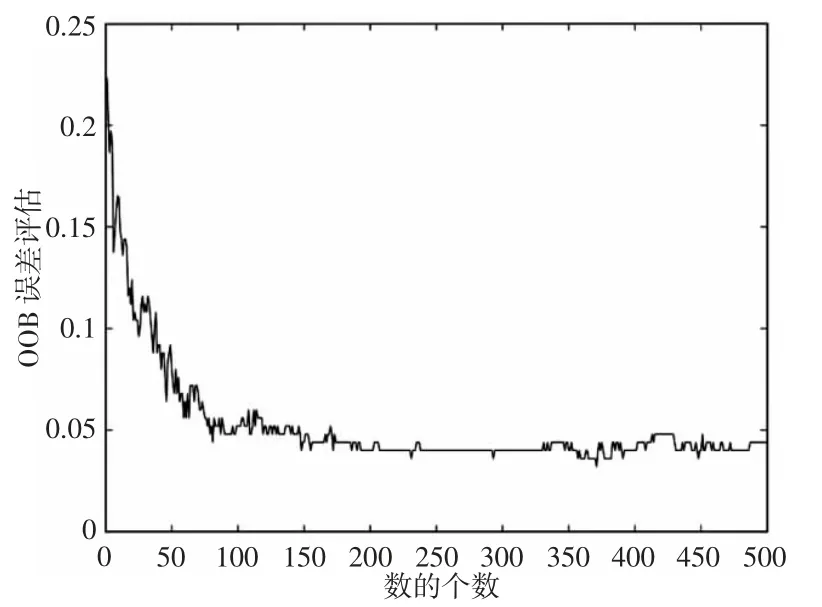
图13 误差曲线图Fig.13 Error Graph

采用VMD-RF 和VMD-SVM 分类器的识别结果图，如图14、图 15 所示。

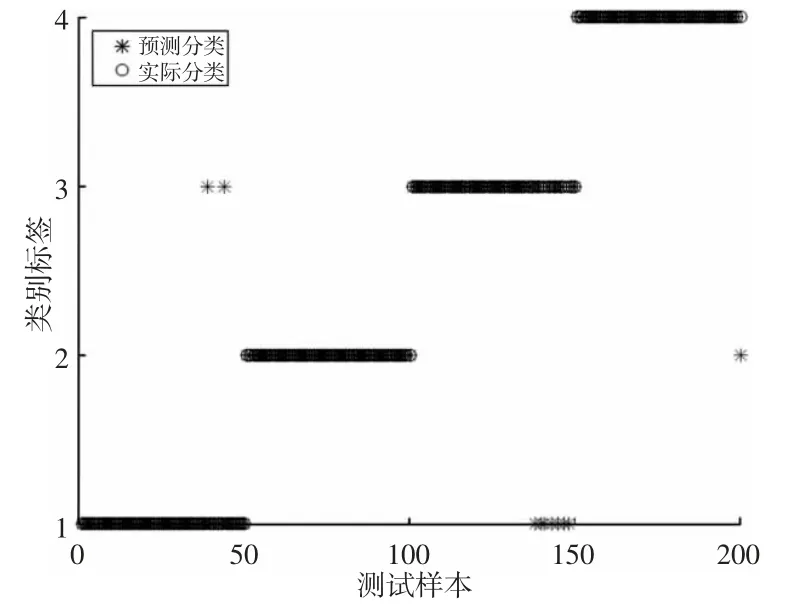
图14 VMD-RF 分类结果Fig.14 Classification Result of VMD-RF

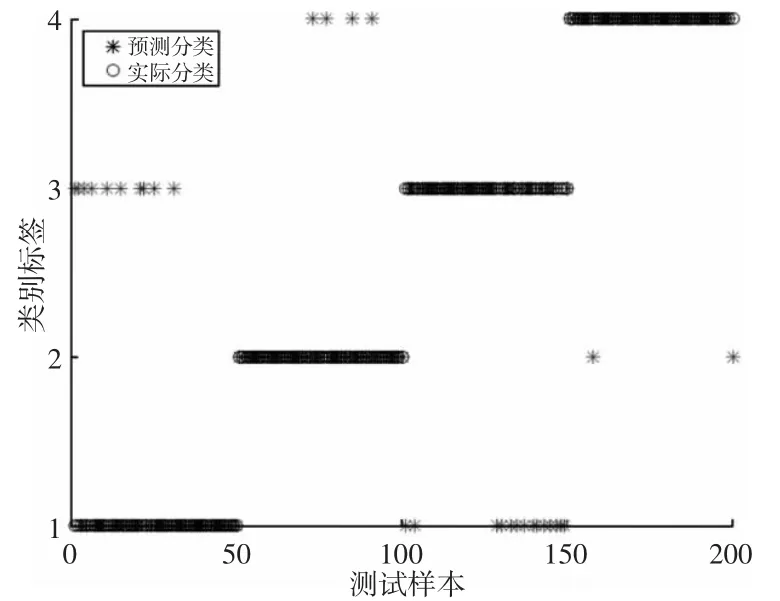
图15 VMD-SVM 分类结果Fig.15 Classification Result of VMD-SVM

从图中看出，采用随机森林对样本进行分类，正常状态的样本中有2 个错误分类，断齿故障的样本中没有错误分类，点蚀故障的样本中存在7 个错误分类，磨损故障的样本中存在1 个错误分类；采用SVM 对样本进行分类，正常状态的样本中有10 个错误分类，断齿故障的样本中有5 个错误分类，点蚀故障的样本中有13 个错误分类，磨损故障的样本中有1 个错误分类。图15 中采用SVM 识别故障，正常状态与点蚀故障易判别错误，点蚀故障误判为正常状态，正常状态误判为点蚀故障，而图14 中采用随机森林识别则明显改善了错判的状况，正常状态下仅2 个错误分类，点蚀故障也从13 个错误分类降低为7 个。最后对测试样本的错误判断个数以及准确率做了统计，如表2 所示。随机森林分类的整体准确率达到了95.5%，与SVM 分类相比，准确率提高了10%，不同状态下的分类精度也明显高于SVM 分类。

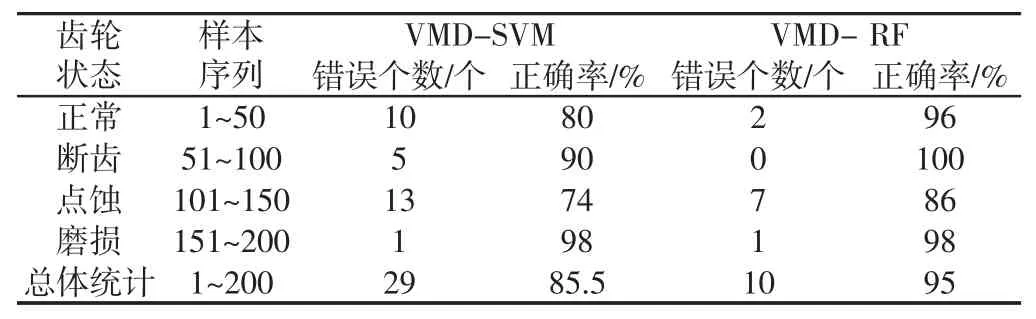
表2 VMD-RF 与VMD-SVM 分类结果对比Tab.2 Comparison of VMD-RF and VMD-SVM Classification Results

8 结论

（1）VMD 作为一种自适应信号处理方法，相对于EEMD 分解，可以有效抑制模态混叠，避免故障信息丢失，特征提取效果更加准确。（2）随机森林将多个单决策树的分类结果集成起来，提高分类精度。基于VMD 能量熵与随机森林相结合的齿轮故障分类准确率高于VMD 能量熵与SVM 结合的方法。由此可见，随机森林在齿轮故障识别方面有着不错的应用前景。