一种非接触式R-test 测量仪球心坐标计算方法
2021-04-02彭炳康吕国艳张历记
彭炳康,吕国艳,江 磊,张历记
(1.西南交通大学机械工程学院,四川 成都 610031;2.中车青岛四方机车车辆股份有限公司,山东 青岛 266000;3.成都飞机工业(集团)有限责任公司,四川 成都 610092)
1 引言
随着零件加工精度要求的提高,对五轴数控机床的几何误差测量也日益重要。针对五轴数控机床的转动轴,准确测量其几何误差是进行误差补偿以提高其加工精度的关键[1]。而对机床转动轴的几何误差测量尚未有专用的测量仪器,目前通常采用球杆仪[2-3]和激光干涉仪[4]进行间接测量,存在测量精度和效率较低等不足。R-test 测量仪可以实时获得安装在机床主轴的测量头相对安装在工作台的底座的三维相对位移误差,并利用五轴数控机床的RTCP 或RPCP 功能,辨识计算机床转动轴的几何结构性误差。R-test 测量仪具有结构简单、测量效率高等优点,可以较好的满足五轴数控机床转动轴的几何误差测量要求[5]。FIDIA、IBS 等公司已有相应的商业化产品,并在行业内得到了较好的应用。
R-test 测量仪主要采用两种测量方式:采用接触式位移传感器进行测量或采用非接触式位移传感器进行测量。在接触式R-test 测量仪方面,文献[6]对接触式R-test 测量装置的工作原理进行了分析,推导了传感器读数与测量球三向位移之间的转换矩阵。然而,由于接触式的测量方式,在机床主轴运动过程中,接触式R-test 测量仪的测量球与传感器之间容易发生磨损[7-8],进而产生测量误差。在非接触式R-test 测量仪方面,文献[9]提出一种了采用非接触式位移传感器的R-test 测量仪,并对该设备的误差辨识算法进行了分析,但未涉及到仪器坐标计算。相比于接触式R-test 测量仪,非接触式R-test 测量仪可以避免测量磨损产生的测量误差,并可以在主轴高速转动条件下进行测量,测量精度、响应性和稳定性都很好,但测量球球心坐标计算算法复杂且尚未完善。
综合考虑非接触式R-test 测量仪的结构及测量原理,针对测量球在测量范围内径向偏离传感器轴线所产生的感应电压特性,提出了球心坐标的计算模型,并采用差分进化算法保证求解的精度和稳定性。通过对比实验,验证所提出球心坐标计算方法的精度和可靠性。
2 非接触式R-test 测量仪结构及原理
非接触式R-test 测量仪的结构模型,如图1 所示。主要包括均匀分布的三个非接触式电涡流位移传感器(ESC)和一个测量球。传感器端部存在一个与传感器轴线垂直的感应平面。设感应平面半径为RECS,测量球半径为Rb,三个感应平面圆心点分别为PE1、PE2、PE3并形成 R-test 测量仪基准平面,传感器仰角(传感器轴线与基准面的夹角)均为α,传感器中心间距(Z轴到感应平面圆心的夹角)均为λ,测量球球心P在第j个位置时,测量球面和球心P到第i个感应平面的距离分别为li-j和Li-j,球心P到第i个传感器中心轴线的距离为ri-j。单个传感器i与测量球的位置示意图,如图2 所示。
为了便于测量计算,建立测量坐标系(MCS),其原点与三个感应平面的距离一致(即原点位于传感器中心轴线的交点),XOY坐标面与基准面平行,传感器1 位于XOZ平面。
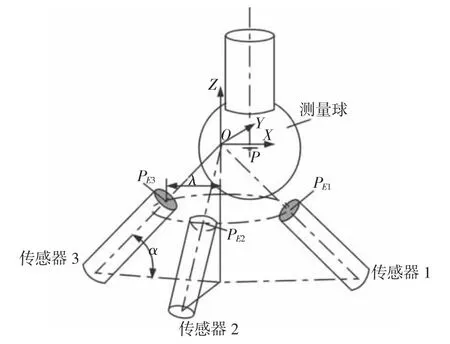
图1 非接触式R-test 测量仪结构模型图Fig.1 Non-Contact R-test Measuring Instrument Structure Model Diagram
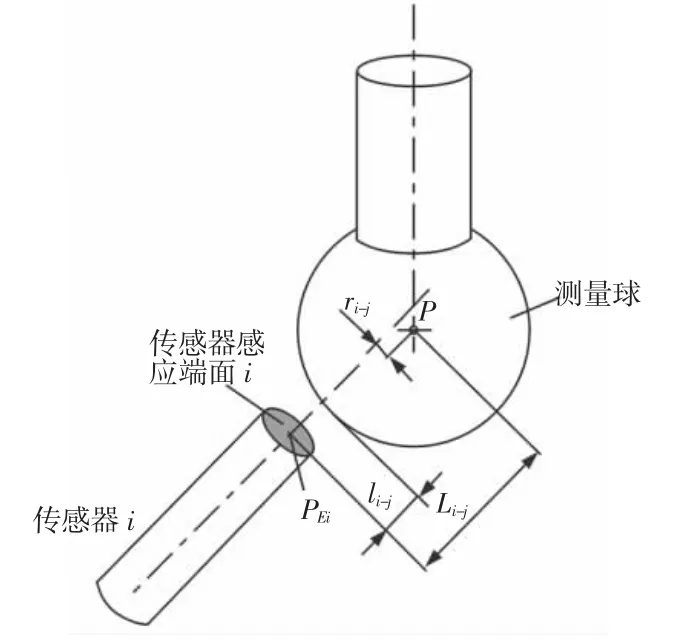
图2 传感器i 与测量球的位置关系示意图Fig.2 Schematic Diagram of the Positional Relationship between Sensor i and Measuring Sphere
传感器轴向量程均为δ,测量球球心在第j个位置时,第i个传感器的感应电压为Ui-j。在传感器轴向量程δ 内,测量球面与感应平面距离li-j的最小允许值为lmin。传感器i的感应电压测量特性方程可表达为:
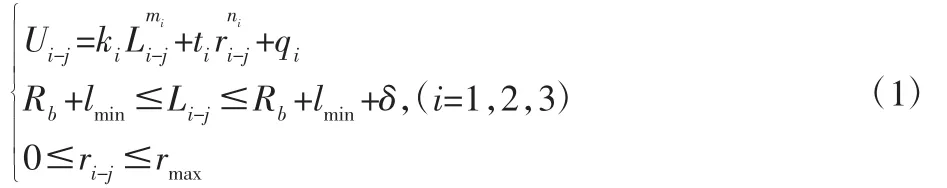
式中:ki、ti、mi、ni、qi—传感器测量特性参数(可通过传感器标定方法获得,由传感器厂商提供);rmax—测量球心偏离传感器轴线距离ri-j的最大允许值(理想情况下球心P点应与原点O重合,但一般情况下球心P(xj,yj,zj)与传感器i轴线存在微量偏离ri-j)。
3 非接触式R-test 测量仪的球心坐标计算模型
根据测量球球心到感应平面距离计算方程、感应平面方程以及球心与感应平面圆心的几何位置关系,如图1、图2 所示。可以构建如下球心坐标计算方程组:

式中:ai、bi、ci和di—第i个传感器感应平面方程系数,(xEi,yEi,zEi)—感应平面圆心点PEi的坐标。通过联立求解方程组(1)和(2),可以得到球心点P(xj,yj,zj)的坐标。
但由于方程组(1)和(2)的求解过程中,测量仪的结构参数、感应电压和传感器系数等均为近似值,常规的方程组求解方法可能无法得到较为准确的计算结果,或者计算结果可能有多个解。为了保证求解结果的精确性,将方程组求解转化为最优值求解问题。由于差分进化算法[10]相比传统的优化算法能在保证计算精度的同时具有计算时间少,鲁棒性高的特点,故采用差分进化算法求解最优值。根据方程组(1)和(2)可以构建如下非线性方程组:
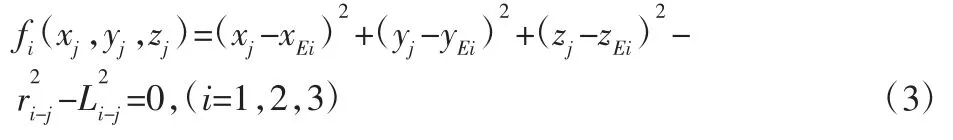
其中,ri-j可转化为关于Ui-j、Li-j的表达式如下,Li-j可用xj,yj,zj表达:
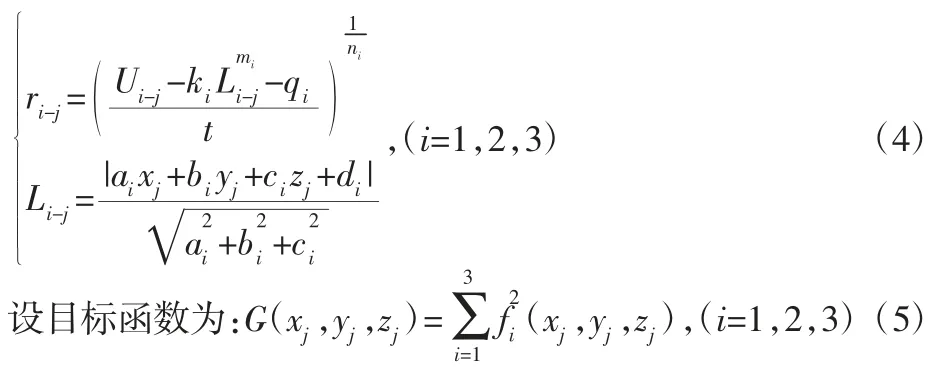
显然,若方程组(3)有解,则目标函数(5)的最小值为零。在算法中,目标函数(5)的值越接近于零,那么对应的方程组(5)的解越精确。采用的差分进化算法参数设定,如表1 所示。
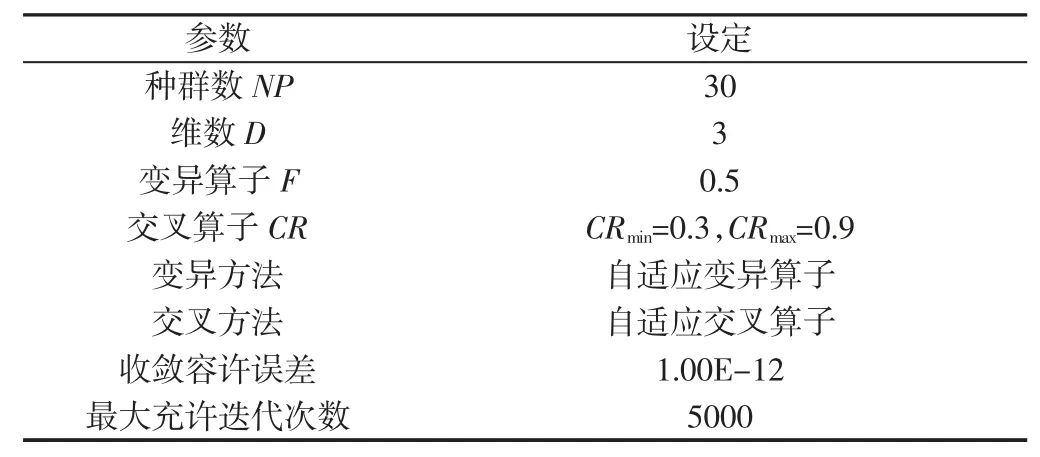
表1 差分进化算法参数设定Tab.1 Differential Evolution Algorithm Parameter Setting
4 应用及验证
为了进行非接触式R-test 测量仪的球心坐标计算方法的应用和验证,开发研制了一套测量仪样机。传感器为Kaman 公司的KD-2306(量程为6mm),测量球直径30mm,测量仪的结构参数中,传感器仰角(传感器轴线与基准面的夹角)为33.69°,传感器中心间距(Z轴到感应平面圆心的距离)为15mm,测量坐标系原点距离感应平面的距离为18.028mm。选择在GF Mikron UCP800五轴机床上进行了一系列对比验证试验(直线轴精度在0.5μm/500mm 以内),测量球通过专用刀柄连接在机床主轴上,仪器固定在机床工作台上,如图3 所示。

图3 非接触式R-test 测量仪实物图Fig.3 Non-Contact R-test Measuring Instrument Physical Diagram
传感器的主要参数为rmax=1.5mm,RECS=7mm,δ=6mm,lmin=0.2mm。感应电压测量特性曲线方程如下:

在确定测量坐标系后,测量仪的感应平面系数及圆心坐标,如表2、表3 所示(可通过传感器感应平面的标定获得)。
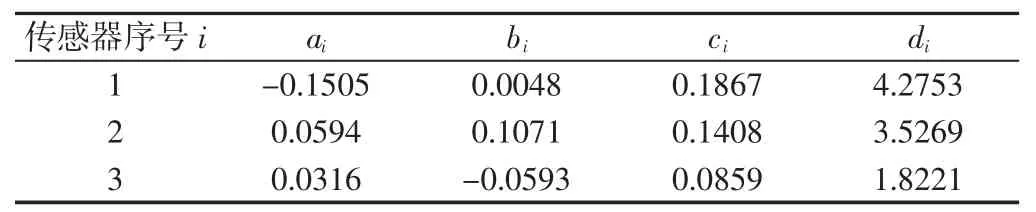
表2 传感器感应平面方程系数Tab.2 Sensor Sensing Plane Equation Coefficient

表3 传感器感应平面圆心坐标(单位:mm)Tab.3 Sensor Sensing Plane Center Coordinates(unit:mm)
通过控制机床平动轴运动,在测量仪的测量空间内移动测量球球心到3 个任意不同的验证点位置(j=1,2,3),各传感器感应电压,如表4 所示。测量球球心位置的实际坐标和计算坐标,如表5 所示。在1.5mm 的测量行程(允许测量球移动的最大位移)内,最大坐标误差为0.39μm/1.5mm。与IBS 等厂家生产的接触式R-test 测量仪 1.5μm/3.5mm 的测量精度相比,0.39μm/1.5mm 完全能满足测量仪的测量精度要求。
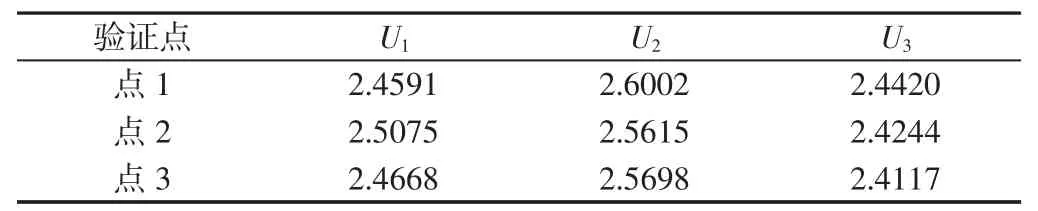
表4 球心在验证点位置的各传感器感应电压(单位:V)Tab.4 Inductive Voltage of Each Sensor at the Position of the Verification Point(unit:V)
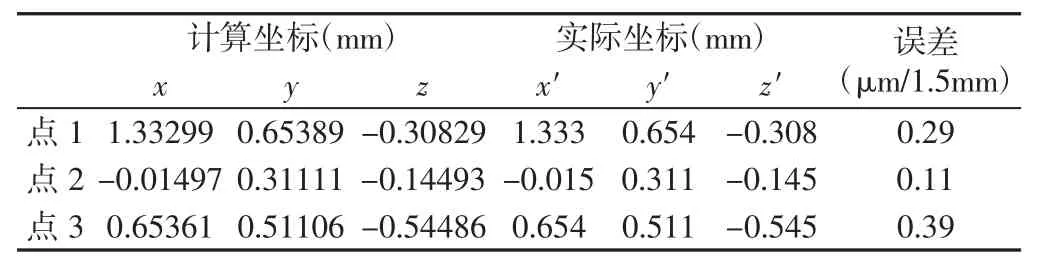
表5 球心验证点的计算坐标与实际坐标对比Tab.5 Comparison of the Calculated Coordinates of the Spherical Center Verification Point with the Actual Coordinates
5 结论
(1)根据非接触式R-test 测量仪的结构特点,建立了测量仪的结构模型并分析了传感器的测量计算原理;(2)提出了非接触式R-test 测量仪的测量球球心坐标计算方法,并分析了差分进化算法最优值求解模型;(3)对测量球球心坐标计算方法进行了应用试验,并进行了计算精度的对比,结果表明所提出的球心坐标计算方法完全满足非接触式R-test 测量仪的测量精度要求。
