堆栈稀疏自编码器的风力机锥齿轮故障诊断
2021-04-02陈里里司吉兵董绍江
陈里里 ,司吉兵 ,董绍江
(1.重庆交通大学机电与车辆工程学院,重庆 400074;2.重庆交通大学城市轨道车辆系统集成与控制重点实验室,重庆 400074)
1 引言
风力机锥齿轮作为风力发电机的重要部件,其工作环境恶劣,故障率较高,在运行过程中容易出现故障,一旦发生故障,将会影响整个风力发电机系统的运行状态以及性能,因而风力机锥齿轮的故障诊断对于风力机的安全运行非常关键[1]。基于振动信号的齿轮故障诊断中,提取特征以及诊断模型的建立是齿轮故障诊断的两个主要问题。在振动特征的提取中,时域分析以及样本熵作为常用的分析方法在很多领域都有着较为广泛的应用[2-5]。在诊断模型的建立中,当前很多诊断模型都局限于浅层结构学习,例如临近节点算法(KNN)[6]、支持向量机(SVM)[7-8]、极限学习机(ELM)[9]以及神经网络等[10]。其局限性主要体现在很难能够获得目标数据深层本质特征以及泛化能力不足等,假如模型的输入特征缺乏足够的表示,将会对结果产生很大的影响。深度学习由文献[11]在2006 年提出,能够有效的解决这一问题。深度学习本质为构建含有多层非线性隐藏层的神经网络,对特征信息进行逐层提取获取目标数据深层本质信息。稀疏自编码器(SAE)作为深度学习中的变形结构,拥有很好的学习数据集特征的能力,通过多个稀疏自编码器堆叠形成SSAE,SSAE 能够进一步的学习目标数据集中的特征,并降低特征维数。当前深度学习已经在很多领域取得了大量成功的应用,例如语音识别、文本语义分类以及图像分类等,但是在齿轮故障信号的识别领域中应用非常少。因而提出了深度学习中的SSAE 模型对风力机锥齿轮数据集进行试验,并对结果进行分析,得出结论。
2 材料与方法
2.1 数据描述
所使用的风力机锥齿轮数据来自于声学与振动数据库,振动数据为使用加速度传感器在功率为3MW 的风力机锥齿轮上进行测量获得,采样率为97656Hz,振动数据共包含24 个振动记录,每个记录长度约为6s,其中共有11 个故障振动记录,13 个正常振动记录。
2.2 时域分析
在故障产生时,齿轮故障位置的刚度将会改变,从而产生振动和冲击,进而导致振动信号的产生。常见的统计特征能够很好的表征在故障产生时的振动信号变化。为了能够表征时域信息,本研究中应用了7 种时域特征分别为均值、方根幅值、均方根值、最大值、标准差、裕度因子以及波形因子,这些特征使用的统计学计算方法,如表1 所示。

表1 时域特征Tab.1 Time Domain Characteristics
2.3 样本熵
样本熵是由Richman 等人提出的一种时间序列复杂性测度方法,样本熵作为近似熵的修正,能够克服近似熵的计算偏差,计算速度更快以及精度更高,适合做机械振动信号的分析。其具体算法如下:
(1)把N个数据构成的时间序列依照序号构建成一个维数为m的向量。
(2)定义Xm(i)与Xm(j)之间的距离d[Xm(i),Xm(j)],其是两个对应元素最大差值的绝对值,计算公式如下:
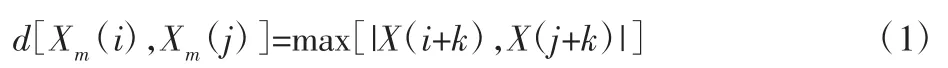
(3)对于已经设置的阈值r,对每一个i值,记录d[Xm(i),Xm(j)]小于r和距离总数N-m的比值,记为计算公式如下:
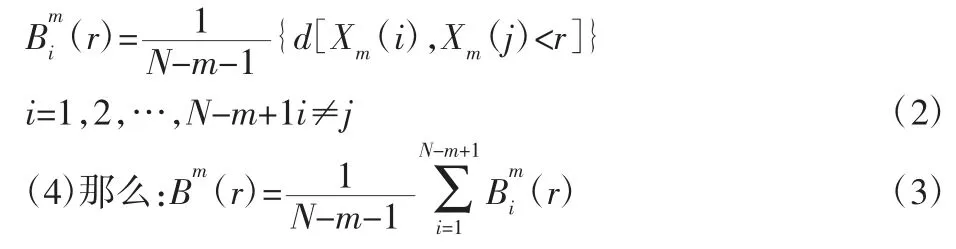
(5)增大维数至m+1,求取Q值,即为计算 Xm+1(i)和 Xm+1(j)≤r的个数,记作Ai。定义:
(6)样本熵定义如下:

能够发现,样本熵的大小和嵌入维数m以及阈值r的数值选取有直接关系。因而m以及r的参数数值对于样本熵的计算有重要影响。因而在计算样本熵时需要首先确定m以及r的数值。
2.4 堆栈稀疏自编码器
2.4.1 自编码器
自编码是一个由输入层、隐含层以及输出层三层神经网络构成的对称结构,如图1 所示。

图1 自编码器结构Fig.1 Autoencoder Structure
自编码器作为无监督特征学习算法,由编码器以及解码器构成,其目标函数是输入。输入向量x经过非线性激活函数f(z)映射到隐含层函数h(x)中,此过程称之为编码,可以使用式(6)进行表示:

式中:W—连接层和隐含层的权重矩阵;b1—偏置单元。
θe={W,b1}是编码器的参数集,在自编码器中,激活函数一般是sigmoid 或者tanh。
隐含层的特征描述经过非线性激活函数g(z)映射成输入空间的重构向量此过程称之为重构,可以使用式(7)进行表示:

式中:b2—偏置单元;WT—隐含层和输出层的权重矩阵。
θd={WT,b2}是编码器的参数集,激活函数的选择依照实际情况可以选择为sigmoid、tanh 或者是线性函数。
x和间的重构误差使用式(8)进行计算,通过反向误差船舶算法调节参数集让误差实现最小。在重构误差最小时,就表明隐含单元保存了输入中的绝大部分信息。
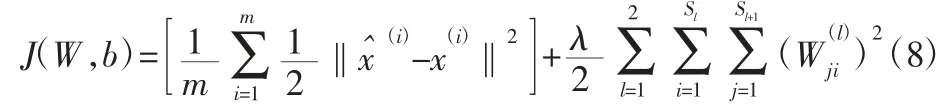
式中:m—训练样本个数;λ—代表权重衰减系数;s1—第一层的神经元数量。
2.4.2 稀疏自编码器
只是为了让无限的逼近x并没有太多意义,为了能够从输入的数据中学习更多有用的特征,要避免自编码器出现学习成一个恒等函数。在自编码器隐含层神经元数量低于输入层神经元数量时,即是欠完备自编码器时,学习欠完备的表示能够让自编码器学习到训练特征的显著压缩特征。但是在h(x)和x的维度一致或者是比x大时,需要给总体代价函数增加稀疏性惩罚项,构建成稀疏自编码器来发现数据结构特点,避免xˆ与x完全相等。稀疏性限制能够让隐含层神经元的激活度控制在一个比较小的范围之内。增加稀疏惩罚项的总体代价函数能够表示为如下:

式中:s2—隐含层神经元的数量;ρj—隐含神经元的平均激活度;ρ—稀疏性参数—隐含神经元j的激活度。
2.4.3 堆栈稀疏自编码器
SSAE 由N个稀疏自编码器堆栈而成,最后一层稀疏自编码器的输出之后和softmax 分类器连接,用来实现故障分类识别功能。在SSAE 训练完成后,将N层稀疏自编码器和softmax 分类器作为整体,用带有标签的样本数据,通过随机梯度下降法来进行监督并调节模型参数,调节过程,如式(12)、式(13)所示。

3 实例分析
3.1 数据预处理
对本研究中的24 个振动记录进行截断处理,11 个已知故障振动记录截断为6281 个样本,13 个正常振动记录被截断为7423个样本,每个样本长度为1024。在所有样本收集完成之后,使用时域分析以及样本熵方法进行提取特征。在本研究中共计算7 个时域特征以及1 个样本熵特征,分别为均值、方根幅值、均方根值、最大值、标准差、裕度因子以及波形因子;在样本熵计算中,嵌入维数m以及阈值r分别选取为2 以及0.2Std(Std 为原始数据的标准差)。
3.2 堆栈稀疏自编码器分类结果
在风力机锥齿轮振动特征提取完成后,构建的SSAE 用来进行风力涡轮机故障诊断试验。首先,故障样本标签设置为0,正常样本标签设置为1,在SSAE 构建以及训练集训练后,进行测试集预测,SSAE 的相关参数,如表2 所示。

表2 堆栈稀疏自编码器相关参数Tab.2 Stacked Sparse Autoencoder Related Parameters
共有2779 个故障样本以及2191 个正常样本被正确预测,如图2 所示。1 个正常样本被错误预测为故障样本,2 个故障样本被错误预测为正常样本。总体来说,基于SSAE 的预测准确率为99.9%。
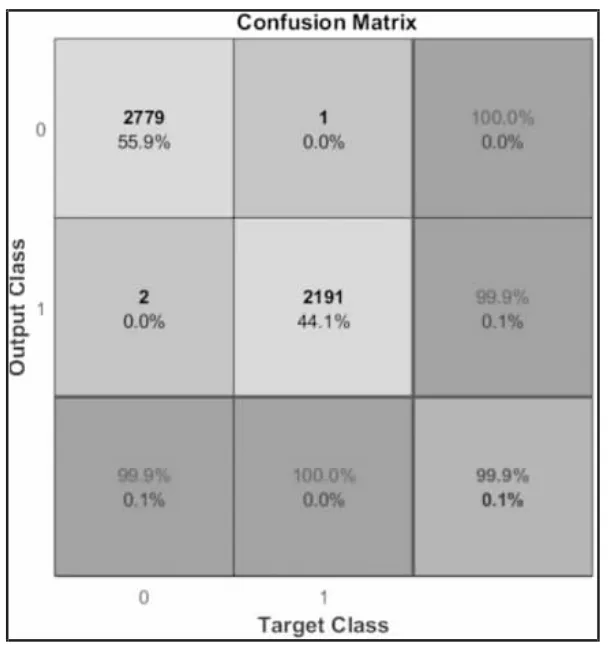
图2 基于堆栈稀疏自编码器的预测结果Fig.2 Prediction Result Based on SSAE
3.3 堆栈稀疏自编码器和支持向量机以及极限学习机对比分析
在本节中,两种分类器(SVM、ELM)被用来和SSAE 进行对比分析。SVM 以及ELM 使用和堆栈自编码器相同的训练集进行训练,使用相同的测试集进行预测,预测结果,如图3、图4 所示。
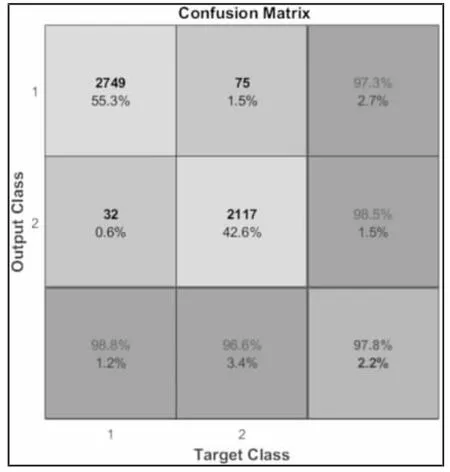
图3 基于支持向量机的预测结果Fig.3 Prediction Result Based on SVM
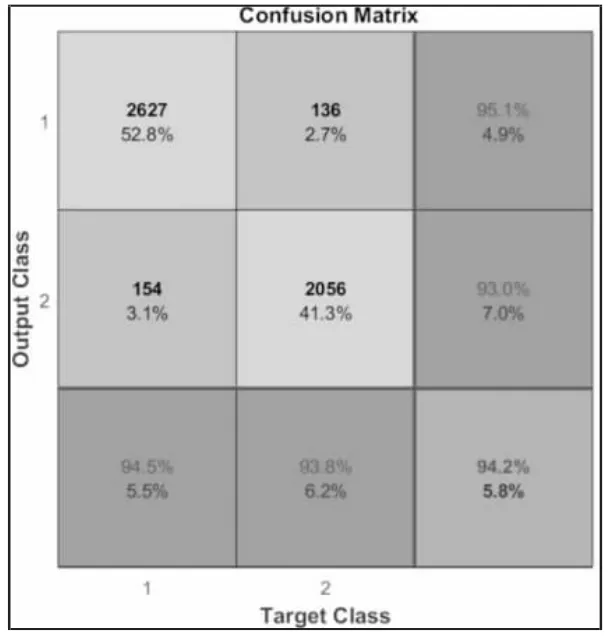
图4 基于极限学习机的预测结果Fig.4 Prediction Result Based on ELM
共有2749 个故障样本以及2117 个正常样本被成功预测,如图3 所示。有75 个正常样本被错位预测为故障样本,32 个故障样本被错误分类为正常样本。总体来说,基于堆SVM 的预测准确率为97.8%。有2627 个故障样本以及2056 个正常样本被正确预测,如图4 所示。有136 个正常样本被错误预测为故障样本,154 个故障样本被错误预测为正常样本。总来来说,基于ELM 的预测准确率为94.2%。因此通过图2、图3 以及图4 对比分析可以得到,SSAE 在分类性能上式要显著优于SVM 以及ELM 的。
为了能够进一步确定SSAE 的分类性能,这里引入了灵敏性(Sensitivity)、特异性(Specificity)以及准确率(Acuracy)三个指标,计算公式,如式(14)所示。除了上述三个指标外,还引入了受试者工作特征曲线(ROC 曲线)用来分类性能的可视化。ROC 曲线描述了灵敏性和1-特异性之间的关系,ROC 曲线下方图形面积越大,分类性能越好。
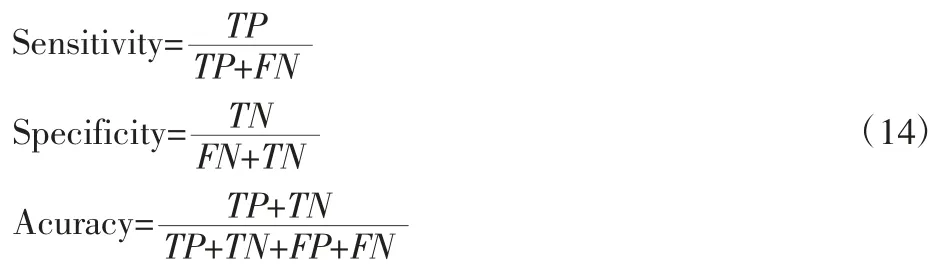
式中:TP—被模型正确预测为正的正样本;
TN—被模型正确预测为负的负样本;
FP—被模型错误预测为正的正样本;
FN—被模型错误预测为负的负样本。
SSAE 的灵敏性、特异性、准确率均显著优于SVM 以及ELM,如表3 所示。因此可以进一步说明,SSAE 模型和SVM 以及ELM 模型相比拥有更好的分类性能。
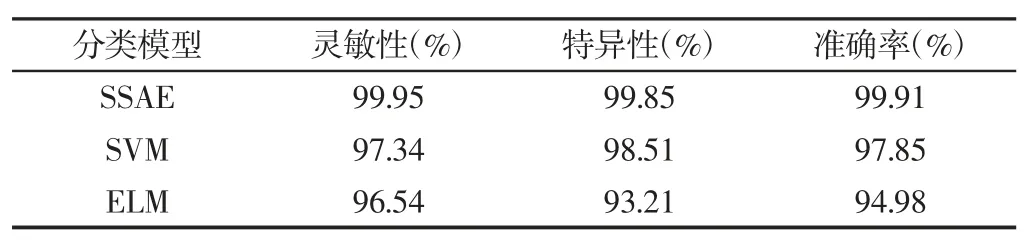
表 3 SSAE、SVM 以及ELM 分类性能对比Tab.3 SSAE、SVM and ELM Classification Performance Comparison
SSAE 模型ROC 曲线下方面积要显著大于SVM 以及ELM模型的ROC 曲线面积,如图5 所示。这表明SSAE 模型的分类性能优于SVM 以及ELM 模型。
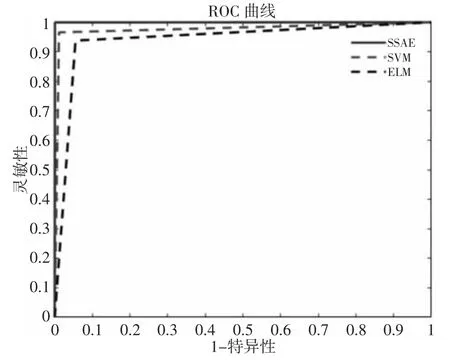
图 5 SSAE、SVM 以及 ELM ROC 曲线图Fig.5 SSAE、SVM and ELM ROC Curve
4 结语
随着可再生能源产业的不断发展,清洁可再生的风力发电技术得到了广泛的关注。但是,风力发电技术在快速发展的同时,也产生了很多的问题,风力发电机故障频发,造成了重大的经济损失。因而进行风力发电机早期故障诊断是非常必要的,风力机锥齿轮作为风力发电机的重要部件,并且工作环境恶劣复杂,故障率较高,因而对其进行研究拥有很现实的意义。通过风力机锥齿轮故障诊断实验结果表明,本研究中所提出的方法和对比模型对比得出,时域分析和样本熵并结合SSAE 以及softmax 分类器方法在风力机锥齿轮故障预测准确率方面至少提高2%,在灵敏性方面至少提高1%,在特性方面至少提高2%,从上述几个指标中可以发现,本研究所使用的方法在上述三个指标中上均有不同程度的提高,因而证实了本研究所提出方法在风力机锥齿轮故障诊断中的优越性。
