齿轮系统动力学模型内部激励参数的优化设置研究
2021-04-02万志国窦益华张明泉李锁斌
万志国,窦益华,张明泉,李锁斌
(1.西安石油大学机械工程学院,陕西 西安 710065;2.西安交通大学机械工程学院,陕西 西安 710049)
1 引言
齿轮传动系统作为一种动力传递装置被广泛应用于航天航空、冶金、化工、交通运输等各个领域中,并发挥着至关重要不可替代的作用。近年来,国内外学者对齿轮系统的振动、噪声及其动力稳定性开展了大量深入的研究。文献[1]利用ADAMS 对齿轮传动系统进行动力学仿真,研究冲击载荷对齿轮啮合力及其频域特性的影响。文献[2]采用集中参数法建立了圆柱齿轮传动系统平移-扭转耦合动力学模型,分析了其振动特性。文献[3]建立了考虑周期时变刚度、齿侧间隙等因素的单自由度直齿轮副系统动力学模型,研究了齿轮系统非线性动力学特性。文献[4]考虑齿轮啮合过程的时变啮合刚度、误差激励等非线性因素,建立考虑单、双啮合变化的直齿轮动力学模型。文献[5]建立了全齿齿侧间隙变化的齿轮传动系统非线性动力学模型,探讨了不同齿侧间隙参数条件下齿轮传动系统吸引子的变化。文献[6]建立齿轮副扭转振动的参数化动力学模型,对裂纹故障的非线性动力学机理进行研究。文献[7]提出一种考虑齿根圆与基圆不重合时的啮合刚度修正方法,建立齿根裂纹动力学模型并进行其振动响应精确求解。文献[8]建立了采煤机截割部齿轮传动系统的非线性动力学模型,研究了啮合刚度、阻尼比及激振频率对齿轮系统动态特性的影响。文献[9]建立了齿轮故障程度的非线性动力学模型,研究齿轮不同故障程度时的非线性振动机理。文献[10]建立了齿轮副系统的动力学模型,研究含不同修形量和修形长度齿轮的动态行为。文献[11]建立了齿轮转子系统动力学模型,研究不同转速下的最佳修形曲线。文献[12]综合考虑齿轮时变啮合刚度及齿轮误差等内部激励的影响,分析了几何参数对齿轮啮合的振动噪声的影响。文献[13]研究了时变啮合刚度对齿轮传动系统扭转特性的影响。文献[14-15]建立了6 自由度的齿轮系统动力学模型,基于时频分析技术分析了裂纹尺寸与系统固有频率之间的映射关系。时变啮合刚度与齿侧间隙等激励源对系统响应产生重要影响。为求解方便,上述研究中通常将时变啮合刚度采用矩形波近似或展开为傅里叶级数,但对没有研究近似简化对齿轮系统动态特性的影响;对于齿侧间隙的研究一部分予以忽略,一部分则采用分段线性函数描述,而对于在什么工况下可以不考虑齿侧间隙,什么工况下必须考虑齿侧间隙还缺少相关方面的研究。因此,为保证故障齿轮传动系统建模参数设置的合理性,有必要研究有关参数对齿轮传动系统动态特性的影响,一方面揭示齿轮传动系统的动力学特性,另一方面为齿轮传动系统动力学精确模型参数的合理简化与设置提供理论依据。
2 齿轮系统动非线性动力学模型
近几十年来,随着齿轮系统动力学的发展,国内外学者针对不同的齿轮动力学问题,提出了诸多不同的动力学模型。而对齿轮传动系统动力学特性的定性分析一般采用简化的齿轮副扭转系统模型。考虑时变啮合刚度、啮合阻尼、齿轮传动误差等因素,齿轮副扭转振动系统动力学模型,如图1 所示。其动力学方程可表示为:
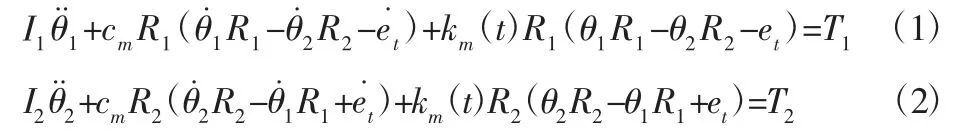
式中:I1、I2—主、从动轮的转动惯量;θ1、θ2—主、从动轮的扭转振动位移;et—啮合轮齿的几何传递误差;T1、T2—作用于主、从动轮的外力力矩;R1、R2—主、从动轮的基圆半径;km(t)、cm—齿轮副的啮合刚度与啮合阻尼。
定义啮合线上的两齿轮的相对位移x为:

从而式(1)与式(2)可以简化为:

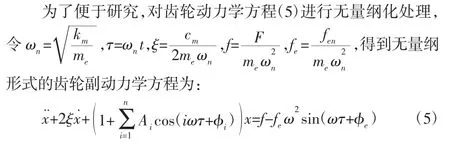
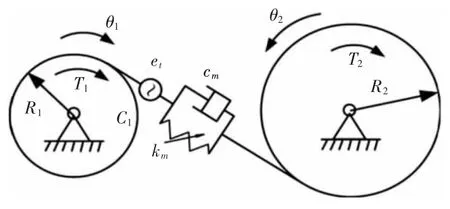
图1 齿轮副系统动力学模型Fig.1 Dynamic Model of Gear Pair System
3 齿轮系统的非线性动态特性
3.1 时变啮合刚度对系统幅频特性的影响
选取阻尼比为ξ=0.05,力f=1,内部激励幅值fe=0.1,时变系统与非时变系统的幅频响应曲线,如图2 所示。由图可以看出,刚度的时变特性使系统响应幅值明显增加;在ω=1 时,时变刚度与时不变刚度模型都会发生系统的共振响应,而在ω 为0.25、0.33、0.5 时,即激励频率为派生系统的固有频率的真分数倍时,时变刚度模型还引起了系统的超谐波共振,可见啮合刚度时变性对系统产生重要影响,在齿轮出传动系统动力学建模时,必须加以考虑。
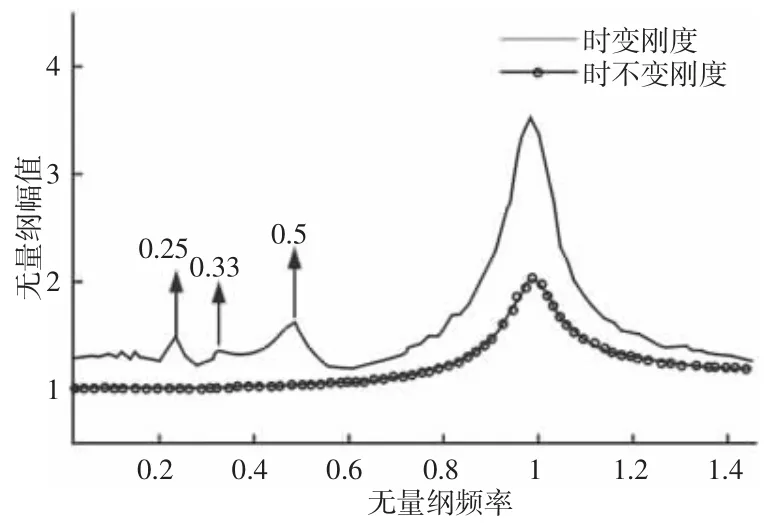
图2 时变刚度对齿轮系统幅频响应曲线的影响Fig.2 Influence of Time-Varying Meshing Stiffness on Amplitude Frequency Response
3.2 时变啮合刚度傅里叶展开级数对系统响应的影响
由于齿轮的单双齿交替啮合,直齿圆柱齿轮的时变啮合刚度近似矩形波,如图3 所示。
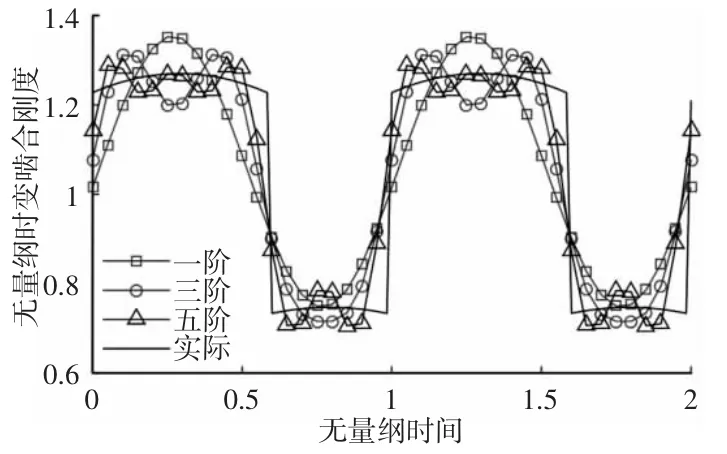
图3 不同阶次啮合刚度的傅里叶级数展开Fig.3 Fourier Series Expansion of Time-Varying Meshing Stiffness
为了研究的方便,通常采用矩形波近似或采用傅里叶级数对其进行展开,但对展开级数无统一标准,将分析傅里叶级数展开阶数对系统动态响应的影响,为齿轮传动系统模型参数的合理设置提供理论依据。
在ω=0.2 时,采用不同阶次的傅里叶级数展开时变啮合刚度后,得到的系统的时域响应,如图4 所示。由图4 可知,随着展开阶次的增加,时域响应中高阶谐波分量逐渐增加,并由简单的谐波响应波形逐渐变化为冲击振动响应波形。显然,直齿轮在低速运行状态下,由于单双齿交替啮合而导致的冲击振动响应更加符合齿轮传动系统的啮合原理。
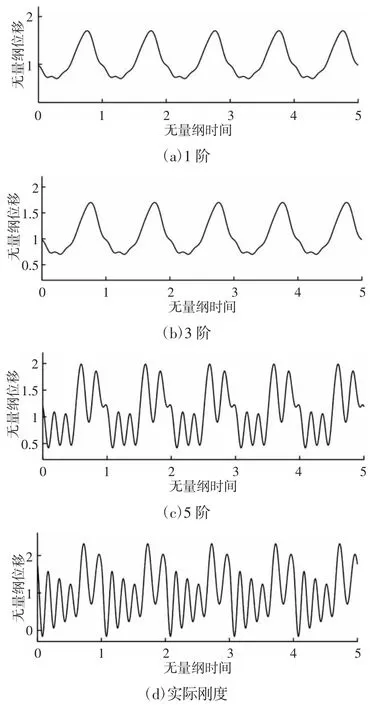
图4 ω=0.2 时不同阶次傅里叶展开时域响应Fig.4 The Time Domain Response Under Different Order Fourier Expansion When ω=0.2
当ω=0.8 时,采用不同阶次的傅里叶级数展开时变啮合刚度后,得到的系统时域响应,如图5 所示。
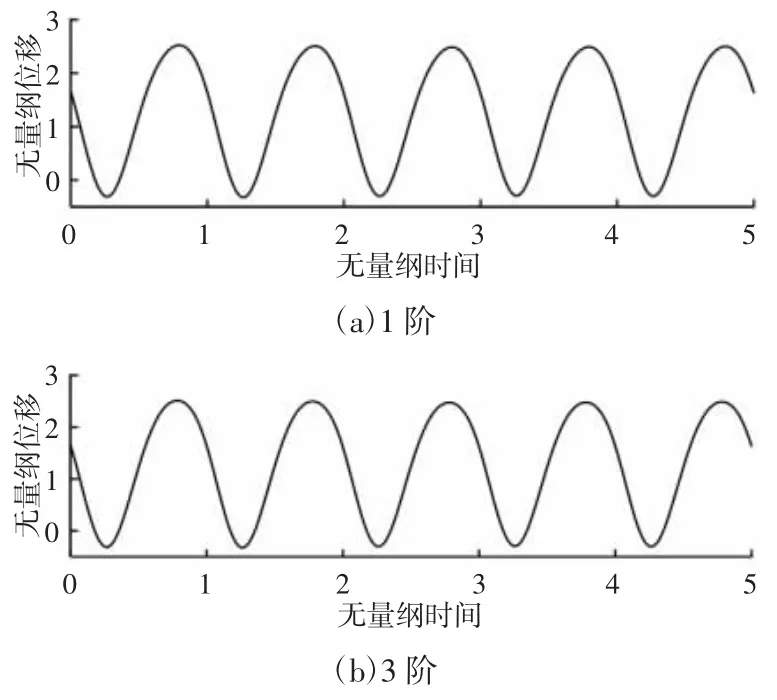
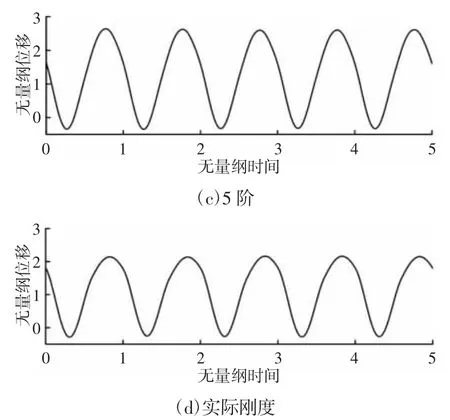
图5 ω=0.8 时不同阶次傅里叶展开时域响应Fig.5 Time Domain Response Under Different Order Fourier Expansion When ω=0.8
当ω=0.8 时,在不同的展开阶次下,时域波形几乎一致,展开阶次对于系统响应的响应并不明显。通过对比分析图4 及图5。可得出如下结论:齿轮在低速运行工况下,系统的响应对时变啮合刚度傅里叶展开阶次更加敏感。因此,在低速工况下分析齿轮传统系统的动态响应时,为了使分析结果更加精确,不适宜对时变啮合刚度做过度地简化。
下面从另一个角度观察时变啮合刚度频率对振动响应的影响。由图4(d)可知,当ω=0.2 时,系统响应中包含有比较明显的冲击振动响应;而由图5(d)可知,当ω=0.8 时,系统响应主要为谐波响应。同一系统在不同的激励频率作用下产生了两种完全不同的响应波形,说明系统响应对啮合刚度激励频率比较敏感,在不同的运行速度下可能产生完全不同的振动。造成这种现象的主要原因是:系统在低速运行状态下,从一对齿参与啮合到下一对齿参与啮合的时间间隔较长,由轮齿单双齿交替啮合而产生的振动冲击有充分的时间响应,系统的振动主要为自由振动与强迫振动响应的叠加,因此时域信号表现为有规律的振动冲击响应,频域表现为啮合频率及其各次谐波。当系统在较高速状态下运行时,从一对齿参与啮合到下一对齿参与啮合的时间间隔较短,由单双齿交替啮合而引起的振动冲击响应相互叠加耦合,系统响应主要表现为强迫振动响应,因此时域信号中主要表现为谐波响应。
3.3 齿侧间隙对系统动态特性的影响
由于齿轮的制造、加工、安装等误差,齿轮使用过程的磨损以及齿轮润滑的需要,在齿轮啮合过程中不可避免的会存在齿侧间隙。对于齿侧间隙的研究,通常采用分段线性系统的理论模型来研究齿侧间隙引起的齿轮传动系统的非线性特性。
齿侧间隙函数可表示为3 个分段线性函数,如果令齿侧间隙为2b,则齿侧间隙函数f(x)可表示为:

考虑齿侧间隙,重写系统的动力学方程:

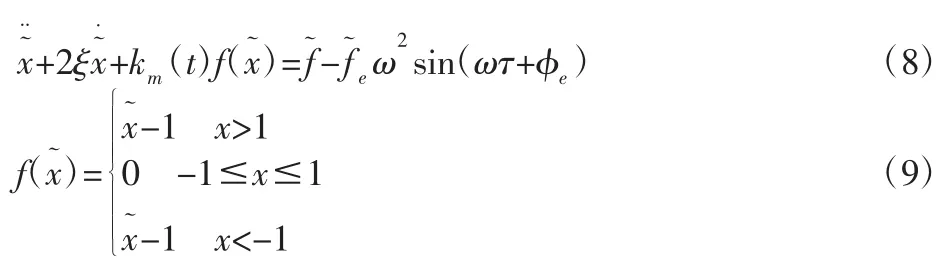
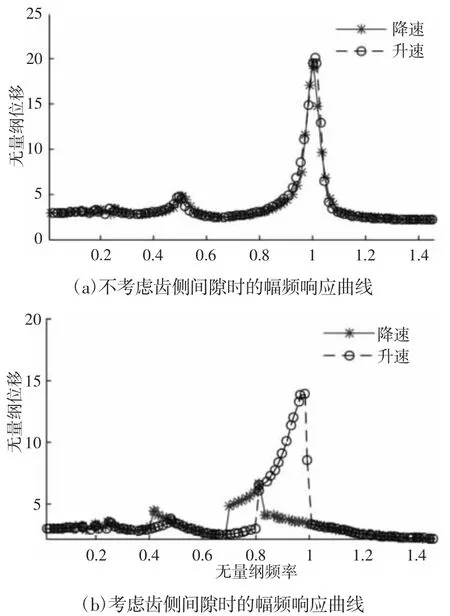
图6 齿轮副系统的幅频响应曲线Fig.6 The Amplitude Frequency Response of Gear System
另外,通过对比图6 可以发现,齿侧间隙对系统动态响应的影响主要体现在ω>0.6 幅频响应曲线的高频段。为了更清晰的阐述这种现象,将低速(ω=0.2)与高速(ω=0.7)状态下,不考虑齿侧间隙时系统响应分别示于图7(a)与图(a)中,考虑齿侧间隙时系统响应分别示于图 7(b)与图 8(b)中。对比图 7(a)与图(b)可知,在低速运行状态下,齿轮系统的响应完全相同。而图对比图8(a)与图8(b)可知,在高速运行状态下,齿轮系统的响应完全不相同。图8(a)所示的振动响应极大值与极小值均大于1,说明系统一直处于无冲击状态(轮齿一侧始终处于啮合状态)。图8(b)所示的振动响应极大值大于1 与极小值小于-1,说明系统处于双边冲击状态(轮齿两侧啮合,存在脱齿现象)。以上对比表明在一定载荷作用下低速运行的齿轮系统,轮齿始终处于接触状态,无脱齿现象,齿侧间隙不会影响系统的动态特性。因此,为了方程便于求解,对于在一定载荷下低速运行的齿轮,建模时可以不考虑齿侧间隙的影,从而简化模型,提高计算效率;而在较高速运行状态下,齿侧间隙对系统影响较大,为了求解精确,必须考虑齿侧间隙。

图7 ω=0.2 时的系统响应Fig.7 The Time Domain Response When ω=0.2
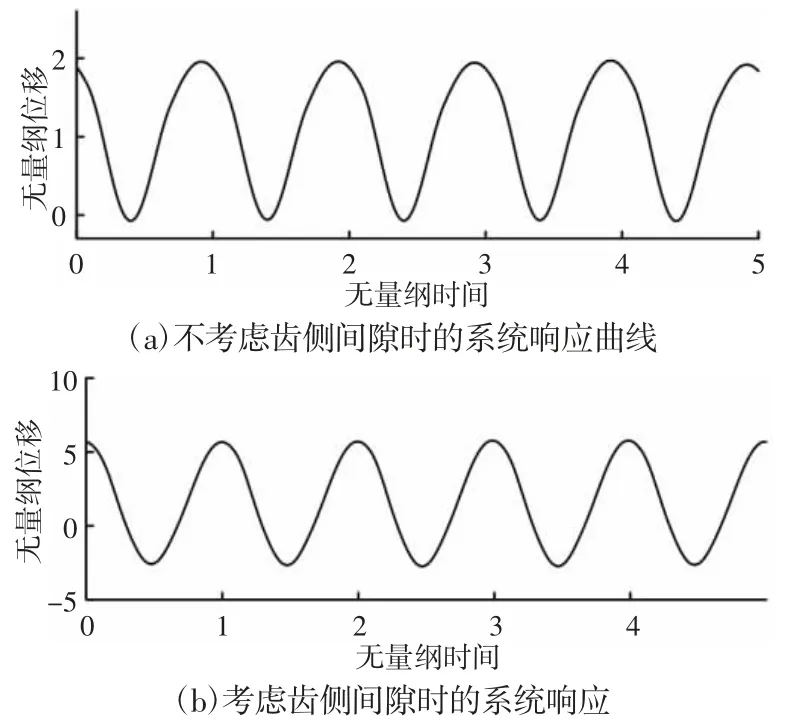
图8 ω=0.8 时的系统响应Fig.8 The Time Domain Response When ω=0.8
4 结论
利用集中参数模型定性研究了齿轮传动系统的主要动力学特性,分析了齿轮传动系统的振动响应特征,为齿轮传动系统动力学模型参数的合理设置提供了理论指导,上述研究取得结论如下:
(1)在时变啮合刚度方面。啮合刚度的时变特性使齿轮传动系统率属于参数振动系统的范畴,使系统表现出强烈的1/2、1/3、1/4 超谐共振现象;随着时变啮合刚度激励频率的增加,齿轮传动系统的时域响应中的自由振动响应逐渐变弱,强迫振动响应逐渐变强。
(2)在齿侧间隙方面。齿侧间隙导致轮齿接触状态发生变化,容易出现脱齿现象,从而使齿轮传动系统的幅频响应曲线表现多值、幅值跳跃等强烈的非线性动力学特性。
(3)在建模参数的合理简化与选择方面。在低速工况下分析齿轮传统系统的动态响应时,不适宜对时变啮合刚度做过度地简化,过度简化将扼杀由单双齿交替啮合而产生的振动冲击响应,与齿轮啮合的原理不符。齿侧间隙对系统动态响应的影响主要体现在幅频响应的较高频段。为了方程便于求解,提高方程求解效率,对于在一定载荷下低速运行的齿轮,可不考虑齿侧间隙;而在较高速运行状态下,齿侧间隙对系统影响较大,为了求解精确,必须考虑齿侧间隙。
