油气润滑ECT 系统的RBF 图像重建算法研究

2021-04-02孙启国闫晓丹

机械设计与制造 2021年3期

孙启国，闫晓丹，钟杰

（北方工业大学机械与材料工程学院，北京 100144）

1 引言

目前，应用于小管径高速环状流油气润滑的ECT 成像算法主要为：LBP 算法及Tikhonov 正则化算法[1]。LBP 算法成像最快，但此算法忽略了灵敏度分布函数与介质分布之间的关联性，从而导致成像失真较大，重建图像伪影严重[2]。Tikhonov 正则化算法可有效解决ECT 图像重建的病态逆问题，但重建图像过分平滑，导致成像区域边界模糊，分辨率较低[3]。

ECT 系统的图像重建是是研究小管径（管道内半径5mm）输送管道内流型等输运特性的重要手段[4-6]。在油气润滑ECT 系统图像重建的过程中，正则化理论可以解决因电容值数量少于像素点数量而引起的不适定问题[7]。RBF 神经网络是由正则化理论推导衍变而来的一种神经网络方法，具有非常强的非线性逼近能力[8]。在此基础上拟采用RBF 神经网络进行油气润滑ECT 系统的图像重建。

2 ECT 系统模型的建立与电容值计算

在油气润滑ECT 系统中一般采用低频率激励，根据物理学中的“似稳原理”可将ECT 传感器视为“似稳场”。利用COMSOL 软件的多物理场仿真环境及电磁理论，求解出不同极板对之间的电容值。

2.1 建立物理模型

考虑到油气润滑实际工况以及小管径的特点，在COMSOL中建立了8 电极的电容传感器及油气润滑管道的3D 物理模型，如图1 所示。根据研究室实验用传感器结构尺寸设计结构参数，如表1 所示。传感器所在物理场由外屏蔽罩、绝缘层、电容极板、径向电极、润滑油及空气等材质构成，环状流管道的径向截面图，如图2 所示。从图中可以看出不同介质的空间分布位置，其中八个电容极板阵列分布在管道壁周围。所有极板与待测极板间存在寄生电容，外屏蔽罩和径向屏蔽电极可起到抗干扰的作用，从而保证了ECT 工作性能稳定。获得更为真实的传感器极板对间电容值。

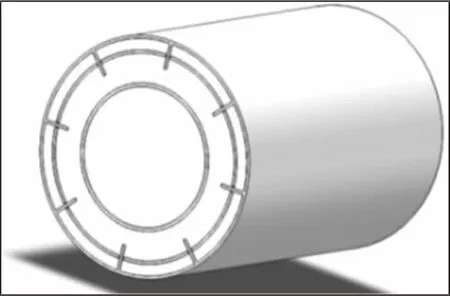
图1 ECT 电容传感器3D 物理模型Fig.1 Three-dimensional Physical Model of ECT Capacitive Sensor

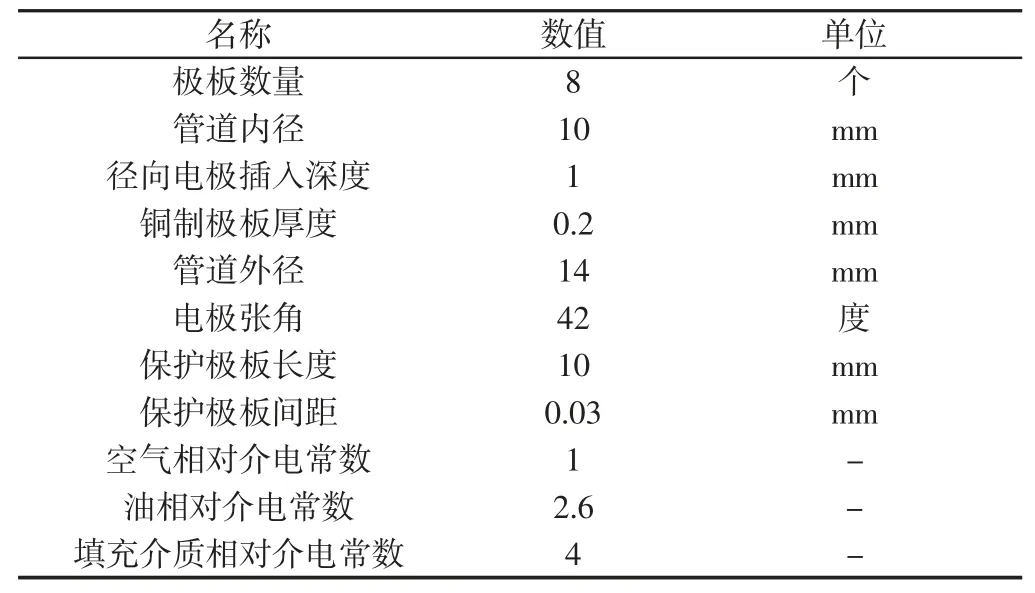
表1 电容传感器的结构参数Tab.1 Structure Parameters of Capacitive Sensor

图2 环状流管道的径向截面图Fig.2 Radial-Section View of Annular Flow Pipe

2.2 求解电容值

油气润滑管道内壁附着一层薄油膜，其流动模式以环状流为主，在只考虑环状流的情况下，预设不同的油膜厚度，根据电磁场基本理论计算电位分布，并求解不同组合极板对间的电容值。

在求解电容值之前，将ECT 系统抽象为数学模型，不失一般性，做以下假设：

（1）在测量过程中，管道内流型保持不变；

（2）外部施加的电场不影响管道内各相介电常数的分布；

（3）传感器及管道空间内无自由电荷。

根据假设条件，传感器内部电磁场可视为静电场，用泊松方程表示为：

以8 电极传感器为研究对象。若源极板为电极i，则Dirichlet边界条件为：

式中：VC—极板激励电压（VC=5V）；Γk、Γi及 Γpg—屏蔽极板、电容极板、保护电极的空间位置。

电场强度为：

由式（3）可知电场方向与电势分布函数的方向相反（仅在测量的敏感场区域内）。

当电容极板的激励端处于高电平时，接收端的极板会产生电荷，因此根据高斯定理可得i，j极板对间产生的电荷量为：

式中：Γ—电极j周围的封闭曲线曲线 Γ 的单位法向量；ε0及ε—空气及润滑油的相对介电常数。

极板受到激励后，电极板i，j之间存在电容，结合式（3）、式（4），电容值表达式为：

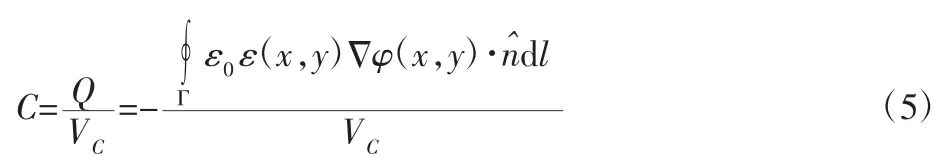
COMSOL 中电磁场分析模块可自动划分场域网格[9]，根据油气润滑ECT 系统敏感场强弱特性，将环状油膜模型设置为3 级网格划分，达到最小网格单元，管道、空气及介质层采用常规网格划分，不同介质之间网格均匀过度，不发生断层，如图3 所示。利用COMSOL 仿真平台内POSTINTERP 函数求解管道内部不同网格点的电势值及等值线，在不同激励下得到各个极板对的电位分布 φ（x，y），结合式（5）即可获得极板间电容值。

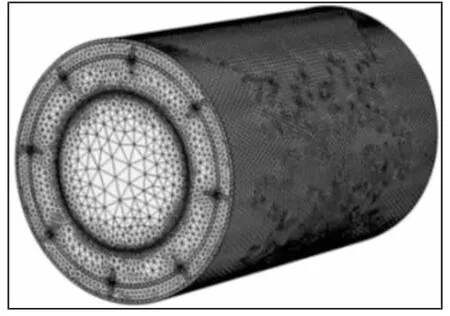
图3 传感器空间网格图Fig.3 Mesh Generation Diagram of Sensor

通过逆时针依次组合极板对，在N极板电容传感器阵列中可得到电容值个数为：

因此，应用于8 电极的油气润滑ECT 系统中，电容值数量为28 个。根据油气润滑ECT 系统的假设条件以及圆形管道外部电极呈均匀分布的特点，故独立电容值个数为4。

3 RBF 神经网络模型

3.1 测量电容的归一化

根据工程实际情况，设定变量油膜厚度h 的变化区间为［0.105～0.500｝（单位mm）。通过改变油膜厚度，采集80 组相关电容值，作为神经网络训练输入样本。

在油气润滑流型中以环状流为主，因此，为了提高计算精度，采用串联模型对80 组测量电容进行归一化处理[10]：

归一化处理前后极板对间电容分布，如图4 所示。

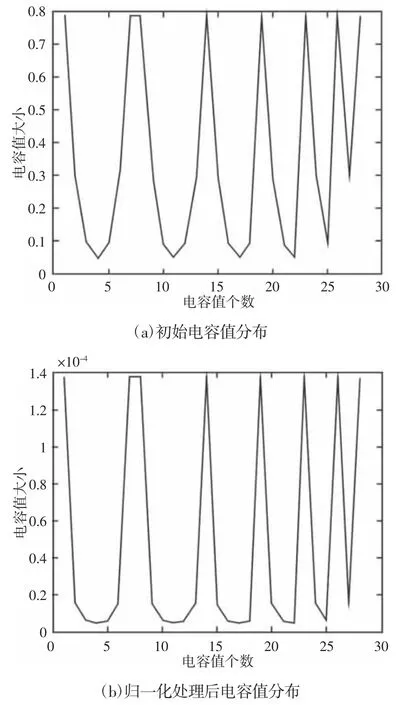
图4 测量电容值的归一化Fig.4 Normalization of Measured Capacitance Values

对比图4 归一化处理前后的纵坐标可知，电容值动态范围显著减小，且能正确反映测量电容本身特征。

3.2 RBF 神经网络的映射与结构

搭建RBF 神经网络结构，其中样本数N=80，输入向量X为归一化电容值，期望输出Y为图像像素灰度值，电容值与图像像素灰度值一一对应。RBF 神经网络结构：

第一层：输入层，即由式（7）归一化处理后的电容值，该电容以28 维列向量作为输入样本，共有80 组；

第二层：隐含层，每组的28 维电容与ECT 成像灰度值之间的映射。该层神经元输出为：

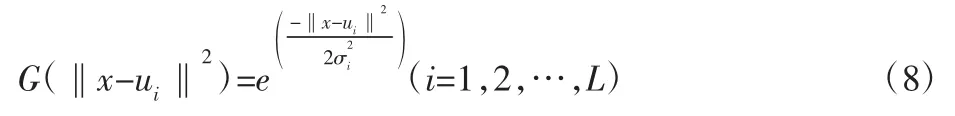
式中：L—隐层神经元个数；x—28 维归一化电容向量；ui—第i个隐层神经元的作用中心；σi—第i个隐层神经元的宽度。

第三层：输出层，对第二层的输出信息进行线性加权，输出润滑油、管道、空气的图像灰度值，共1600 个像素点。该层输出为：

式中：G—1×s维网络输出向量，该输出向量为1600 维图像灰度矩阵；G—1×L维隐含层输出向量；W—L×s维权值矩阵。

通过计算确定RBF 网络的三个参数：基函数中心向量、基函数宽度以及隐含层与输出层间的连接权重[11]。最后反复训练网络，直至网络误差达到预设误差（这里误差设为1.0×10-3）或者达到最大训练步数。将训练好的RBF 算法打包离线，可极大提高重建速度，满足油气润滑ECT 系统对实时性的要求。

4 图像重建仿真与结果分析

4.1 图像重建仿真

对油气润滑管道进行仿真，取高低介电常数相对的介质的灰度值分别为1 和0。图像重建的过程灰度值会出现大于1 或小于0 的像素点，因此加入灰度滤波，取灰度滤波阈值为0.2，预测像素灰度值大于0.2 被定义为高像素灰度值1，反之则定义灰度值为0。

4.2 仿真结果分析

设定4 组不同介质无间隙相接的随机样本，油膜厚度成递增趋势。针对同一模型，分别使用LBP 算法、Tikhonov 正则化算法和RBF 算法对随机样本进行图像重建结果，如表2 所示。RBF算法可以减小LBP 算法重建图像的失真度，有效解决Tikhonov正则化算法重建图像的边界模糊问题，使重建图像更清晰。