广义执行器馈能主动悬架研究
2021-04-02王政皓王玉顺
王政皓,柳 江,王玉顺,滕 乐
(青岛理工大学机械与汽车工程学院,山东 青岛 266520)
1 引言
馈能主动悬架能实现悬架的能量回收和改善悬架的平顺性,是车辆底盘研究的热点之一。馈能悬架将传统悬架的减振器耗散的能量进行回收,以增加汽车能量供给,能够更有效的提高车辆的能量利用效率。
目前馈能悬架形式多样,主要分为电磁式、液电式、气压式三种主要形式。文献[1]提出滚珠丝杠式馈能减振器,通过滚珠丝杠实现运动形式的转换,将悬架的振动能量转化为电能进行存储;文献[2]提出一种基于电动静液压作动器的馈能悬架,悬架的振动转化为液压回路液压油的运动,从而带动液压马达与电机的连接,实现电能的回收。
考虑能否利用一个模型一个算法来实现良好的适应性,以实现快速切换硬件形式。因此,提出一种基于广义执行器的馈能主动悬架,从能量转化的本质(将悬架振动的机械能转化为其他形式的能量)和主动控制的本质(即通过控制电机电流实现对主动力控制)的角度,对馈能主动悬架进行数学化建模,以悬架的姿态作为自变量,建立统一的广义功/能模型,对馈能悬架进行研究分析。
2 广义执行器控制方法
以1/4 悬架为基础,提出的基于广义执行器的馈能主动悬架模型,图中的作动器为广义执行器,具有馈能与主动控制两种状态,当悬架处于馈能模式,广义执行器将悬架振动的能量进行回收,所回收的能量称为广义功/能,当悬架处于主动控制模式,广义执行器为悬架提供主动控制力,如图1 所示。广义执行器具体工作流程图,如图2 所示。由图2 中可知,采用广义执行器的设计流程首先进行参数定义,确定广义参量kj和Gj以及广义变量qj和rj的取值,代入到广义执行器模型,然后设计控制算法,计算悬架性能指标以及馈能效率,实现车辆的主动控制以及悬架振动能量的回收。若效果不理想则重新调整广义参量kj与Gj,再次带入广义模型进行计算,直到馈能主动悬架达到预期效果。其核心思想在于:忽略掉不同主动/馈能悬架实际物理结构的差异,从数学上建立一个统一的模型和固定的算法,即将物理参数通过参数定义的方法直接转化为数学参数,代入统一的模型和控制算法中进行优化,实现改善悬架性能和能量回收的功能。
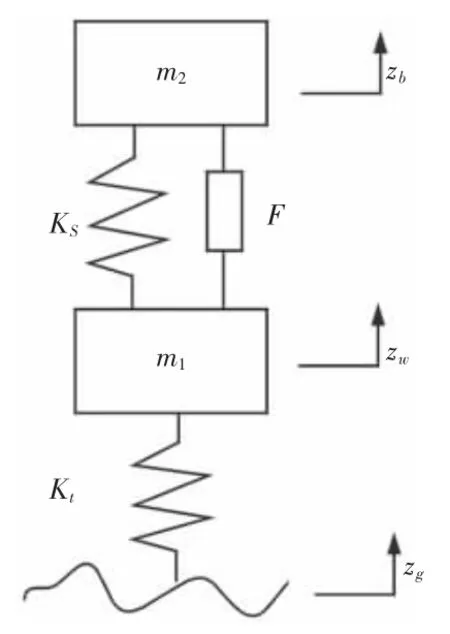
图1 广义执行器悬架模型Fig.1 The Suspension Model of General Actuator
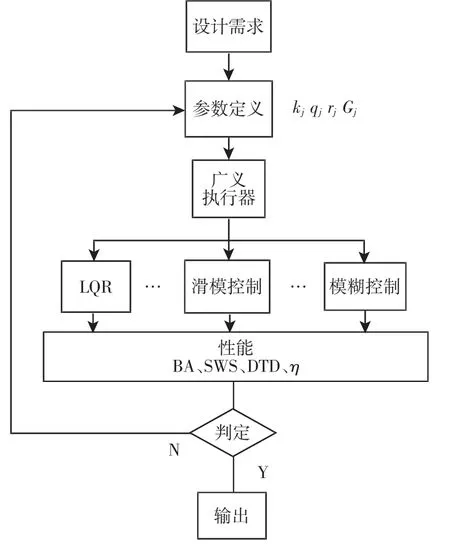
图2 广义执行器流程图Fig.2 Flow Chart of General Actuator
传统的馈能主动悬架设计流程,首先需要根据设计需求确定馈能悬架的物理类型(通常有电磁式、液电式、气压式、飞轮惯性式种),然后选择结构类型(如滚珠丝杠、摇臂式、并联机构等),再选择控制算法(如模糊、滑模、遗传算法等),最后通过仿真分析得出性能指标,若不能达到预期效果,需再次重复以上的选择过程,直到达到预期效果。
二者相比,基于广义执行器的设计流程更接近线性结构,对软件和硬件的要求较低;而传统的设计流程更接近遍历树状结构,要保证模型选择的精确性,必须保证树状图的广度,增加了运算的复杂度,对设计人员的经验依赖性较大。对于设计过程的标准化自动化而言,遍历树的方法必须保证数据库的全面性,且需要对数据库随时更新,提高了对软件和硬件的要求。
也可从信息熵[3]的角度进一步对比。在传统的方案选择过程中,每一次的选择都会降低其所包含的信息量,增加离散程度,提高熵值。假设经过n1种物理类型选择后,其包含的信息占总信息的1/n1,如果每一个物理类型都包含n2种结构类型,则经过结构类型的选择之后,所包含的信息仅为总信息的1/n1n2,假定控制算法有1/n3种,则经过控制算法选择之后,包含的信息仅为总信息1/n1n2n3,根据熵值公式可知传统执行器的熵值:

图2 所示的方法经过一个完整的设计流程后,所包含的信息仅为总信息的1/n3,根据熵值公式可知广义执行器的熵值:

从熵值原理可知,基于广义执行器的设计流程的熵值更低,减小了设计的不确定性。
3 三类馈能减振器模型分析
3.1 电磁式
电磁式馈能减振器主要由运动转换机构与电机的串联组成,运动转换装置将悬架的垂直运动转换为旋转运动,带动电机进行能量回收,以滚珠丝杠式馈能减振器为例,进行电磁式馈能减振器的建模。
电磁式馈能减振器的电学和力学方程为[4]:

式中:EM—电动机电动势—滚珠丝轴向速度;φ—丝杠电动机常数,φ=k/l;k—电动机常数;l—丝杠导程。感应电动势EM与感应电流I满足关系:

式中:R—电机内阻与外接负载阻值之和。
电磁式馈能减振器的馈能功率为:

式(3)与式(4)联立可得作动器的阻尼力:

3.2 液电式
液电式馈能减振器主要通过悬架的振动引起液压缸上下腔压力的变化,从而引起液压马达的转动,带动电机的转动,进行能量回收。
液电式馈能减振器的电学方程为[5]:

式中:Ke—电动势系数;w—电机角速度;Td—电机转矩;—电机角加速度;Kt—电磁转矩系数。
液压马达与输出转矩满足:

且由液体流量连续方程可得:

式中:n—液压马达转速;q—排量;vg—活塞杆的速度也即;ηv—容积效率;ηm—机械效率。
液压缸的阻尼力为:F=△PA
若忽略液压管路的压力损失,则:

由于液压马达与电机串联,因此:
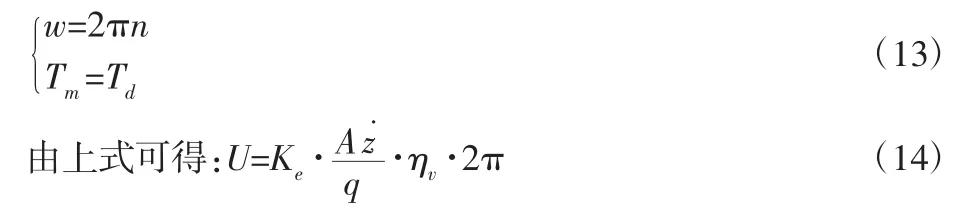
若忽略电机转动惯量:
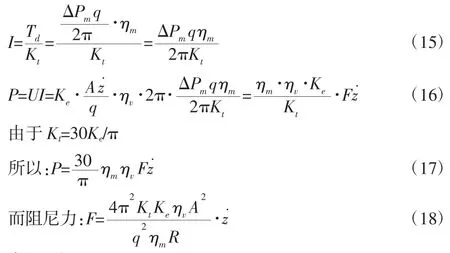
3.3 气压式
气压式馈能减振器主要通过悬架的振动驱动往复式空气压缩机的活塞杆从而获得高压气体,进行储藏和利用。
往复式空气压缩机的力学模型为:

理想往复式空气压缩机的工作过程,如图3 所示。
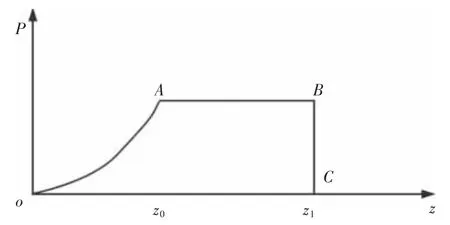
图3 气压式馈能悬架的工作过程Fig.3 The Work Process of Pneumatic Energy-Regenerative Suspension
图3 中OA段为气体压缩阶段,伴随着活塞杆的移动气体进行压缩,气压升高达到所需压力值POUT,AB段为排气过程,将所需压力的气压能进行储藏,BCO段为进气过程。
对应空气压缩机工作过程的能量图,如图4 所示。
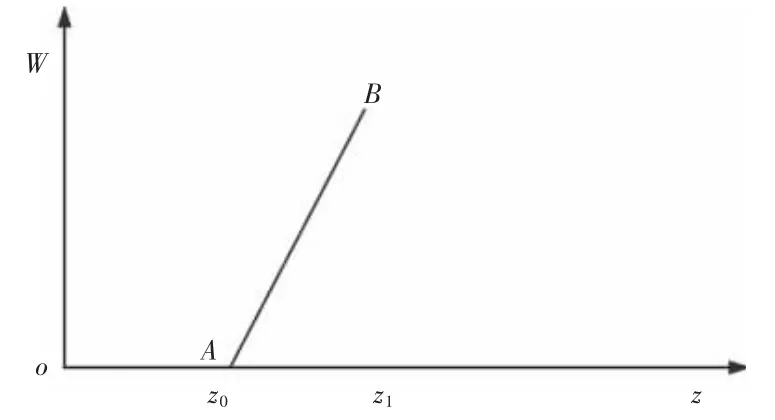
图4 气压式馈能悬架的能量图Fig.4 The Energy Chart of Pneumatic Energy-Regenerative Suspension
图4 中OA段为气体压缩阶段,AB段为排气阶段,获得所需高压气体,为整个过程的有效做功过程。
结合上图可知,做功W与活塞位移z为分段函数:
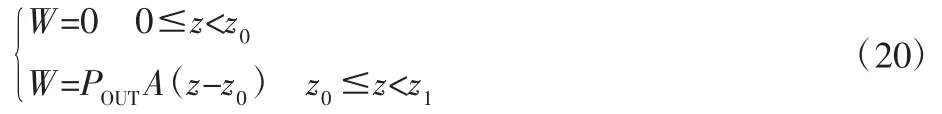
4 广义馈能主动悬架模型
4.1 广义馈能模型
综合电磁式、液电式、气动式三种馈能减振器的特点,三者的共同点都是通过将悬架振动的机械能转化为其他能量进行储存,因此,忽略其结构和形式的因素,将三种形式馈能悬架的结构作为定参,建立统一形式的馈能减振器模型,广义执行器的输入为悬架的振动,输出为能量。
将式(5)与式(6)联立可得:

将式(17)与式(18)联立可得:

从式(21)与式(22)可知,电磁式与液电式皆可写成一个自变量为,因变量为功率P的函数。考虑到气动式馈能减振器的介质为空气,空气存在可压缩性的特征,难以建立功率P与的关系,因此考虑建立有效功W与悬架动行程z的关系。但从式(20)可知,气压式馈能减振器的功有效功W与悬架动行程z的关系呈现为一个分段函数,为使气动式馈能悬架的能量公式与电磁式和液电式相统一,如图5 所示。在能量图中添加抛物线OB且使OAG所围成的面积与GB所围成的面积相等,用抛物线OB代替OA-AB作为气动式馈能悬架的能量曲线。
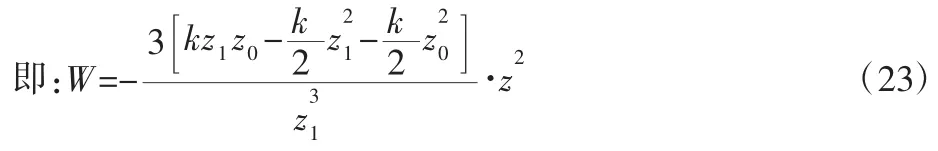
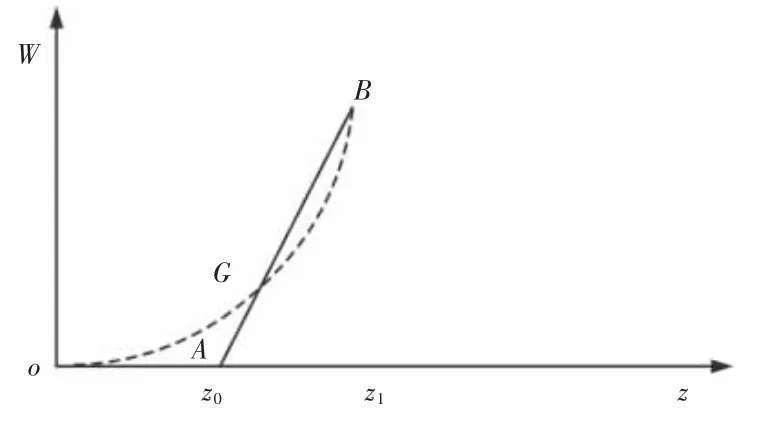
图5 气压式馈能悬架能量图Fig.5 The Energy Chart of Pneumatic Energy-Regenerative Suspension
结合式(21)~式(23)建立统一的一般模型为:

对式(24)进行变形,可得到广义化公式:

式中:Qj—广义功/能;qj—广义坐标;kj—广义参量。
4.2 广义主动控制模型
悬架实现主动控制的核心为作动器提供主动力,电磁式与液电式均需采用电机进行能量回收,因此可利用直流电机既可作为电动机又可作为发电机的特性,由直流电机提供主动力,而气压式减振器,则通过控制排气阀开启压力的大小得到主动控制力。主动控制力模型为:
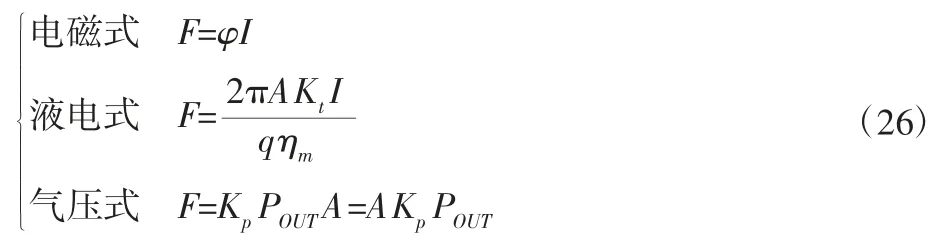
由于气压式馈能减振器存在传动介质的可压缩性,存在力传递的滞后问题,因此,添加压力修正系数KP来对力主动力F与POUT的关系进行修正。KP是与作动器结构参数有关的系数,可由实验获得,这里KP的取值为1.15。
与4.1 节类似,可对式(26)进行变形,得到广义化公式:

式中:Fj—控制力;Gj—广义参量;rj—广义控制元
5 LQR+GA 控制算法
由图1 可知,1/4 车辆模型的动力学模型为[6]:
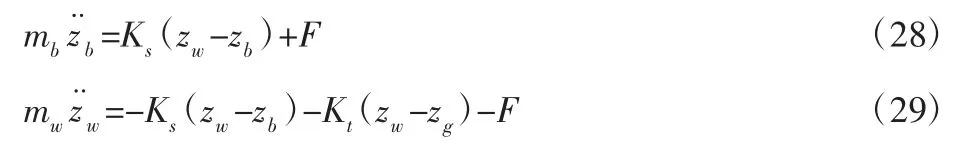
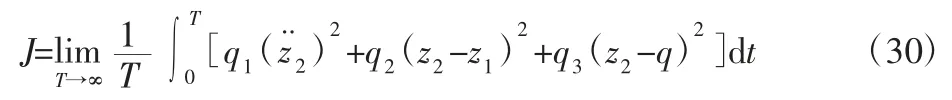
式中:q1—车身加速度加权系数;q2—悬架动行程加权系数;q3—轮胎动位移加权系数。
将式(30)写成标准二次型:
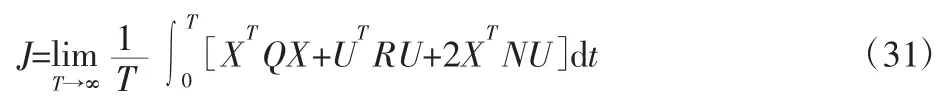
其中,状态变量加权矩阵

对于最优控制反馈增益矩阵K的求解,可以采用黎卡堤方程求出:
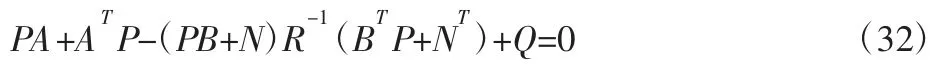
最优控制反馈增益矩阵K=R-1(BTP+NT)由车辆参数和加权系数决定。K的求解,可以通过Matlab 的LQR 函数得到[7]:

式中:S—黎卡堤方程的解;E—系统闭环特征根。
得到最优控制反馈增益矩阵K通过反馈状态变量X(t),可以得到最优控制力U(t):

在传统的LQR 控制算法中,其最优性取决于加权矩阵Q,R的选择,而矩阵中的加权系数q1,q2,q3完全是人为的[8-9],因此,传统的LQR 算法并不是完全意义上的最优控制,这里通过采用遗传算法,对加权系数q1,q2,q3进行优化,以得到完全最优控制。
这里取遗传算法的适应度函数L为[10]:

式中:BA,SWS,DTD—车身垂向加速度、悬架动行程,轮胎动位移的均方根值;BAb,SWSb,DTDb—被动悬架的相应性能;X—加权系数q1,q2,q3。
遗传算法的参数设计,如表1 所示。

表1 遗传算法参数设置Tab.1 The Parameter of GA
6 仿真分析
对上述广义执行器模型进行仿真验证,路面选择为D级路面,仿真的主要参数,如表2 所示。

表2 仿真参数表Tab.2 Parameters of Simulation
仿真得到车辆车身加速度,悬架动行程,轮胎动位移的仿真曲线,如图6~图8 所示。其相应的均方根值,如表3 所示。所得到的广义功/能及馈能效率,如表4 所示。由仿真图表可知,基于广义执行器的馈能主动悬架与被动悬架相比,车身加速度的均方根值降低了24.3%,悬架动行程降低了6.9%,轮胎动位移降低了5.6%,改善了辆的平顺性。由表4 可知,广义功/能以及馈能效率与广义参量有关,当广义参量为K1时,广义功率(即馈能功率)为22.02%;当广义参量为K2时,广义功率为15.3%;当广义参量为K3时,广义功率为17.05%
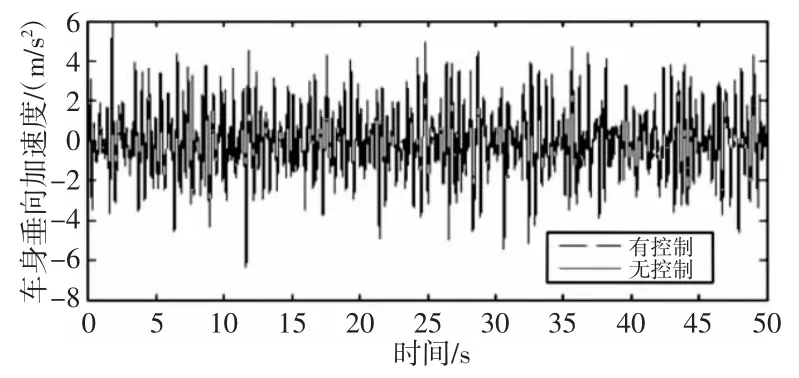
图6 车身垂向加速度Fig.6 Body Acceleration
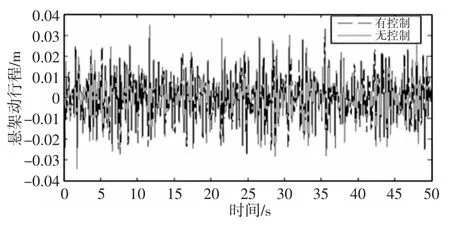
图7 悬架动行程Fig.7 Suspension Working Space
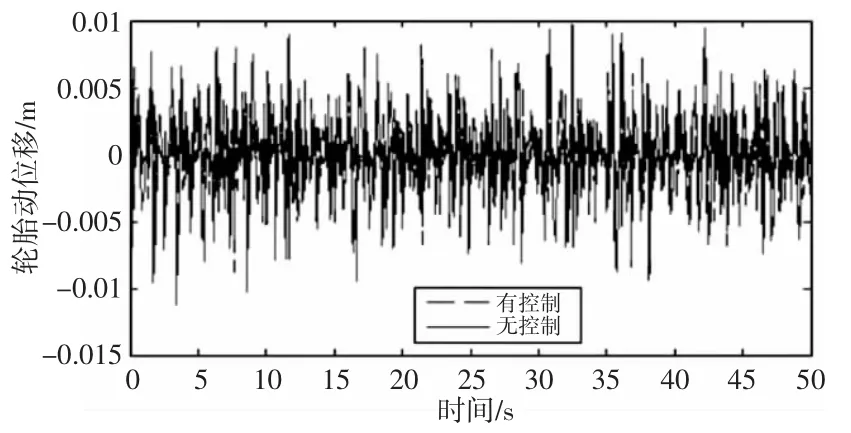
图8 轮胎动位移Fig.8 Dynamic Tire Deflection
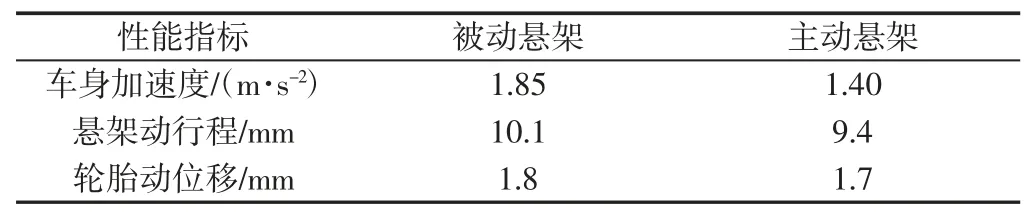
表3 悬架性能均方根值Tab.3 Suspension Performance Root-Mean-Square Value
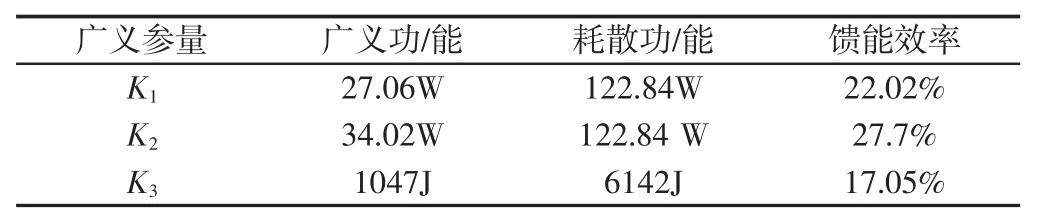
表4 馈能效率Tab.4 Energy-Efficiency
7 结论
(1)根据广义功/能与广义力模型,利用LQR+GA 算法实现悬架的馈能与主动控制,仿真结果表明该种方案可行,除了能获得15%以上的馈能效率,也可以将车身加速度的均方根值降低24.3%,悬架动行程降低6.9%,改善车辆的平顺性和乘坐舒适性。
(2)电磁、电液式的馈能模型有形式相似度极高的物理/数学表达式,气压式馈能模型物理意义与前述两个显著不同,利用拟合曲线等工程方法可以获得类似的数学模型。
(3)所获得的广义模型,具有统一的简洁的数学表达形式,既能表征主动悬架核心的作动力,也能表征馈能悬架核心的功能效率,适应性较好。该模型涵盖了常见的三种主动悬架、馈能悬架类型,也可进一步将惯性飞轮等其他形式逐步纳入其中。
(4)基于广义执行器馈能主动悬架的设计流程相比传统设计流程,减少了对设计人员经验的依赖和硬件软件的要求,且有更低的信息熵,更小的不确定性。
