刚性飞轮转子-基础耦合系统的径向振动分析
2021-04-02任正义杨立平
任正义,黄 同,杨立平
(1.哈尔滨工程大学工程训练国家级实验教学示范中心,黑龙江 哈尔滨 150001;2.哈尔滨工程大学机电工程学院,黑龙江 哈尔滨 150001)
1 引言
所有旋转机械都分为转子和定子两部分,磁悬浮飞轮系统中的定子包括电磁轴承座,电机定子,安装支架等[1-2]。磁悬浮储能系统在工作调试过程中,一般将定子部分安装在刚性基础上,通过建立静止坐标系来研究分析飞轮转子的运动。但随着旋转速度越来越高,转子的振动会不可避免地影响到基础支架,产生基础激励进而影响自身的振动响应。
文献[3]以涡轮增压器转子-轴承系统为模型,分析了基础激励对转子动力学特性的影响。文献[4]分别研究了安装基础振动对七自由度和五自由度车载飞轮转子振动幅值的影响。文献[5]通过单次平衡技术识别转子-轴承-基础系统的激励和柔性支承参数,并通过实验进行了验证。文献[6]分别从理论和实验上研究了柔性转子系统在受到基础激励后的弯曲动态特性。大多数基础激励分析都将其看作为一个固定方向的激励力,没有分析基础支承特性对转子的振动影响,因此这里建立了600Wh 磁悬浮飞轮-基础系统的径向耦合动力学方程,分别分析了飞轮转子转速和基础径向支承刚度对定子和转子振动的影响。
2 安装支架结构
600Wh 磁悬浮飞轮转子系统与安装支架的结构示意图,如图1 所示。储能系统结构布局,如图1(a)所示。系统的转子部分沿轴向方向分别为上保护轴承,上径向电磁轴承,轴向磁轴承,飞轮转子,电机/发电一体机,下保护轴承,定子部分则包括各转子部件的支座,真空冷却系统,安装支架等[7]。安装支架的相关参数,如图1(b)所示。安装支架设置了四个与地面接触的安装支点a1、a2、a3、a4,其中四个支点分别距离支架中心轴l,上下径向电磁轴承中心分别与支架底部中心相距h1,h2。

图1 储能飞轮整体结构布局图Fig.1 The Overall Structure Layout of Energy Storage Flywheel
为了便于分析系统转子和定子的运动矢量,需要建立相应的坐标系和支承参数,如图2 所示。图2(a)中上下径向电磁轴承与定子之间等效为弹簧-阻尼元件,其中上下刚度和阻尼参数分别相同,两个参数各自用kf和cf表示。储能飞轮系统径向受到激励会影响安装支架的初始形态,所以同样地将
安装支架在安装点之间等效为弹簧元件,刚度为ks。假设磁悬浮飞轮系统在平衡状态下弹簧和阻尼的伸长量为零。图2(b)表示的是建立运动方程所需要的基本坐标系,首先为了能够在同一坐标系下描述系统定子和转子的运动矢量,建立一静止坐标系OXYZ与大地固连在一起,其位置以坐标系oxyz为参考,o为安装支架底部的中心点,oz为支架中心线,ox和oy为沿着支架底部径向方向两个相互垂直的坐标轴,系统在初始时刻和平衡状态时,坐标系OXYZ与oxyz重合。然后分别建立相应的定子坐标系osxsyszs和ofxfyfzf转子坐标系,其中转子坐标系中的of是飞轮转子的几何中心点,定子坐标系中的os是上下径向电磁轴承距离中点,同时还设置了上径向电磁轴承坐标系o1x1y1z1和下径向电磁轴承坐标系o2x2y2z2,当转子处于平衡位置时,转子坐标系与定子坐标系重合。

图2 飞轮转子支承与坐标系Fig.2 The Support and Coordinate System of Flywheel Rotor
3 耦合动力学方程
对于考虑基础激励的刚性飞轮转子耦合系统,采用拉格朗日方程推导耦合运动方程[8]。首先需要求出定子和转子在静止坐标系下的位移和速度矢量。为了方便运动矢量在各坐标系下的相互转换,引入坐标变换矩阵:

当定子受力发生振动时,其位移矢量在静止坐标系下表示为us={xs,ys,zs}T,平动速度为此时忽略定子绕oz轴的转动,只考虑绕ox轴和oy轴的倾斜,定义径向倾斜角度角度αs和βs,假设定子的径向倾斜过程为先绕ox轴转动αs角,再绕oy轴转动βs角,则定子倾斜角速度在静止坐标系下表示为:
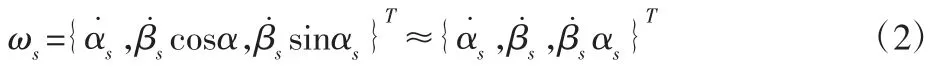
定子坐标系下的倾斜角速度为:

式中:‘*’—定子坐标系下的矢量表达。因为不考虑定子绕oz轴转动,式中的
从定子的倾斜角度中可以求出定子坐标系到静止坐标系的转换矩阵Tsg。

分析飞轮转子在定子坐标系os xs ys zs下的运动矢量,磁悬浮飞轮在坐标系o1x1y1z1和o2x2y2z2中的转子位移分别为x1、x2、y1、y2,由此得到其在osxsyszs坐标系下位移为:

平动速度为:

同样定义转子的径向倾斜角度αf和βf:

相应地类似式(2)和式(3)得到转子在坐标系os xs ys zs和of xf yfzf中的倾斜角速度:

式中:‘**’—转子坐标系下的矢量表达。
由转子坐标系of xf yf zf到定子坐标系os xs ys zs的坐标变化矩阵和反变换矩阵:
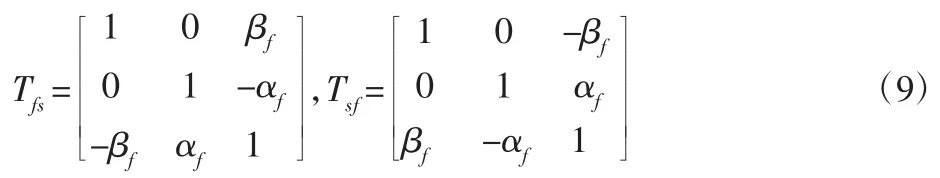
转子坐标系下定子倾斜角速度矢量为:

静止坐标系中飞轮转子的位移矢量为:


为了便于建立耦合动力学方程,设广义坐标为:

定义定子动能表示为Ts,转子动能为Tf,得到:

对刚性飞轮转子和定子来说,假设:

式中:Jsd,Jsp—储能系统定子的赤道转动惯量和极转动惯量;Jfd,Jfp—储能系统转子的赤道转动惯量和极转动惯量;ms,mf—安装支架质量和飞轮转子质量。
此时系统的总动能表示为:

由于这里不考虑系统轴向运动,忽略了重力势能。因此系统势能为:

其中,x1、x2、y1、y2由下式确定:

系统粘性阻尼耗散能为:

联立以上公式,并代入Lagrange 方程式:

将飞轮转子自转角速度Ω 看作一常数值,整理式(21)即可得到磁悬浮飞轮-基础耦合系统的运动微分方程。由于飞轮转子位移参数变化范围很小,所以将运动方程进行线性化处理,即得到耦合运动方程为[9]:
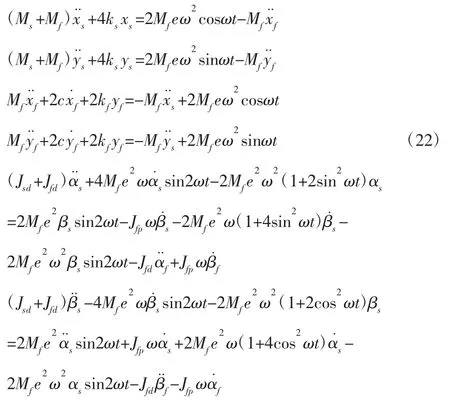

其中式(22)为耦合系统平移运动方程,式(23)为耦合系统倾斜运动方程。
4 径向振动分析与试验数据分析
4.1 仿真分析
根据式(22)和式(23)所建立的磁悬浮飞轮-基础耦合运动方程来分析转子系统的径向振动响应。其中600Wh 磁悬浮飞轮与安装支架参数,如表1 所示。
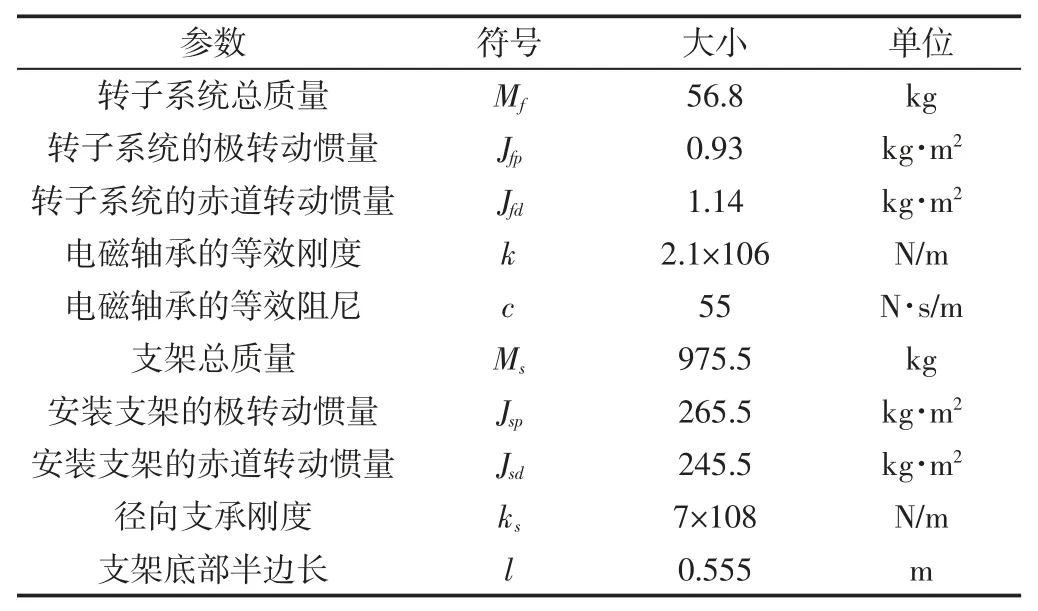
表1 磁悬浮飞轮与安装支架参数Tab.1 The Parameters of Magnetic Suspension Flywheel and Mounting Bracket
首先将上式参数代入方程中计算出耦合运动下转子的径向平动固有频率为44Hz,倾斜固有频率为205Hz,与第三章中求解的结果相比增大了一些。平台的径向平动固有频率为269Hz,倾斜固有频率为108Hz,由于支架的支承刚度只存在于下方,所以振型先是发生倾斜然后是平移,与转子恰好相反。
4.1.1 飞轮转速
随着飞轮工作转速的提高,其振动响应会通过支承系统传递到基础支架上,引起支架相对于地面的振动,从而对自身的振动也产生了一定影响。因此这里选取了三个不同转速ω=100π,200π,400πrad/s,分别分析了各个转速下定子和转子的振动响应,其中径向平移振动图,如图3 所示。径向倾斜振动图,如图4所示。最终得到了飞轮转速对耦合振动的影响。

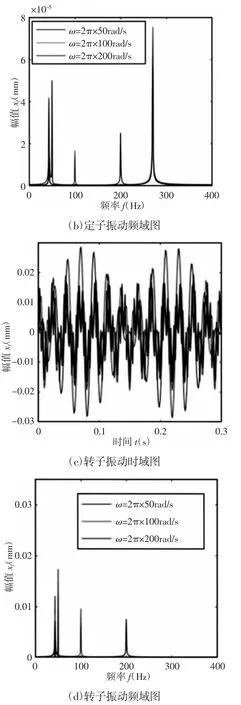
图3 不同转速下耦合系统径向平动振动响应Fig.3 Radial Translational Vibration Response of Coupled Systems at Different Speeds
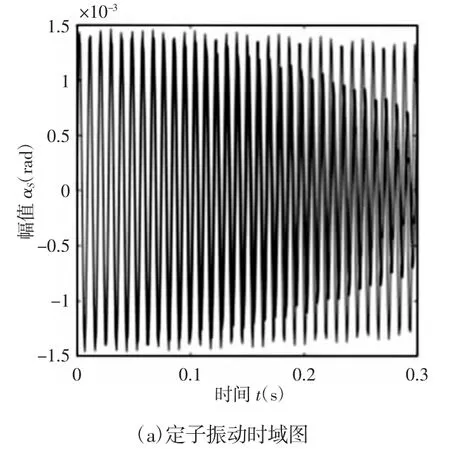
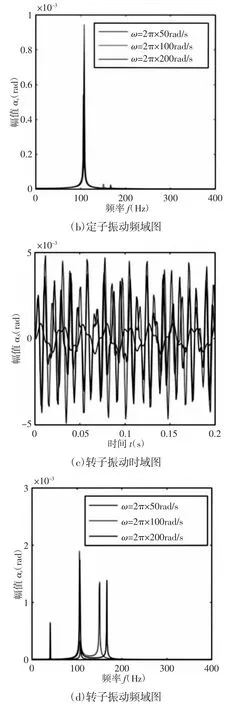
图4 不同转速下耦合系统径向倾斜振动响应Fig.4 Radial Tilt Vibration Response of Coupled Systems at Different Speeds
不同转速下定子径向平动分别受到转子平动固有频率、不平衡量、定子平动固有频率三个激励,如图3(a)、图3(b)所示。其中当转子转速ω=100πrad/s 时接近转子的平动固有频率,转子产生了共振,这种现象也传递到了定子,使定子在该转速下振幅达到最大。越过转子平动临界转速后,转子不平衡量对定子的激励随着转速增加而增加,但变化并不明显,表现在100Hz、200Hz 下的振幅中,说明定子振动中,转子不平衡量产生的同频信号不是主要频率成分。定子平动固有频率269Hz 信号下的振幅也受到了转速的影响,转速在低速100πrad/s 到200πrad/s 之间,振幅随着转速增加而增加;转速在转速200πrad/s 到400πrad/s 之间,振幅随着转速增加而减小。不同转速下转子受到不平衡量,平动固有频率两个信号激励,转子转速接近固有频率时的振幅最大,随着转速的增加,振幅变小,定子平动对转子平动也没有明显的影响,如图 3(c)、图 3(d)所示。
不同转速下定子径向倾斜主要受到定子倾斜固有频率108Hz 信号的激励,如图 4(a)、图 4(b)所示。转速为 ω=200πrad/s时,该激励下的振幅最小,且变化速度最快,说明转子转速会影响定子倾斜运动;转子倾斜的陀螺力矩信号也对定子倾斜有一定的激励,但与108Hz 信号相比来说很小。转子倾斜振动不仅受到陀螺力矩的影响,如图4(c)、图4(d)所示。定子支承特性所决定的108Hz 信号也对转子产生了激励,当转子转速ω=200πrad/s 接近定子倾斜固有频率时,83Hz 下的振幅最大,这说明定子倾斜特性对转子倾斜振动有一定影响。
4.1.2 基础径向支承刚度
从式(22)和式(23)中可以看出,耦合运动方程中的基础径向支承刚度ks会对系统振动有影响,因此本小节通过调整支架的支承刚度来分析系统振动响应。取转子转速6000r/min,且认为支架各径向支承刚度相同,分析了不同ks条件下转子的振动响应及频谱图,如图5~图6 所示。

图5 不同ks 条件下的转子6000r/min 径向平移振动响应Fig.5 Radial Translational Vibration Response of Rotor 6000r/min under Different ks Conditions
分别取ks=7×108,108,107N/m 进行分析。安装支架的支承刚度越小,转子径向振动响应会变大,但影响程度并不明显,如图5(a)所示。不同ks条件下转子振动响应所包含频率分量的区别,当ks=108N/m 时,转子的不平衡量激励幅值明显减小,如图5(b)所示。这是由于该支承刚度条件下支架的径向平动固有频率为100Hz,此时支架产生了共振,从而导致转子在定子坐标系中的偏移量减小;当ks=107N/m 时,支架的径向平动固有频率为32Hz,这引起了转子在30Hz 附近的一个低频激励。转子在6000r/min状态下的倾斜运动时域图和频域图,如图6 所示。图6(a)中转子的倾斜振动响应随着支架径向支撑刚度的减小而增大,且变化较为明显。图6(b)中三种支承刚度条件下陀螺力矩产生的频率分量不变,当ks=107N/m 时,平台倾斜固有频率为14Hz,因此在低频产生了一个较大的幅值激励;当ks=108N/m 时,固有频率分量为41Hz,此时振幅明显减小,两个频率分量幅值也相差不大;当ks=7×108N/m 时,108Hz 附近出现了一个小连续谱。

图6 不同ks 条件下的转子6000r/min 径向倾斜振动响应Fig.6 Radial Tilt Vibration Response of Rotor 6000r/min under Different ks Conditions
由以上分析得出,基础的径向支撑刚度影响着转子的径向振动响应,其中对于转子倾斜运动幅值的影响更为明显,平动振型下平台的固有频率与转子转速同频时转子振动幅值最小,倾斜运动振型下低频区频率分量越低,幅值越大。
4.2 试验数据分析
600Wh 磁悬浮飞轮储能系统样机,如图7 所示。其中包括安装基座、飞轮本体样机、电/发一体机、控制箱系统(功率放大器、电压调理板、DSP 控制板等)、电磁轴承控制器和数据采集系统等。其中转子数据提取主要经过位移传感器输入主板控制信号从主板另一端输入转子线圈,另一边的传感器通过检测电流转化为电压信号输入采集系统,控制电流i与转子位移变化Y通过控制系统建立联系,如图8 所示。试验过程中取采样频率f=3000Hz,分别分析了转子转速在3000r/min,6000r/min 时的振动数据,如图 9~图 12 所示。

图7 飞轮储能系统样机Fig.7 Flywheel Energy Storage System Prototype

图8 转子位移控制图Fig.8 Rotor Displacement Control Chart
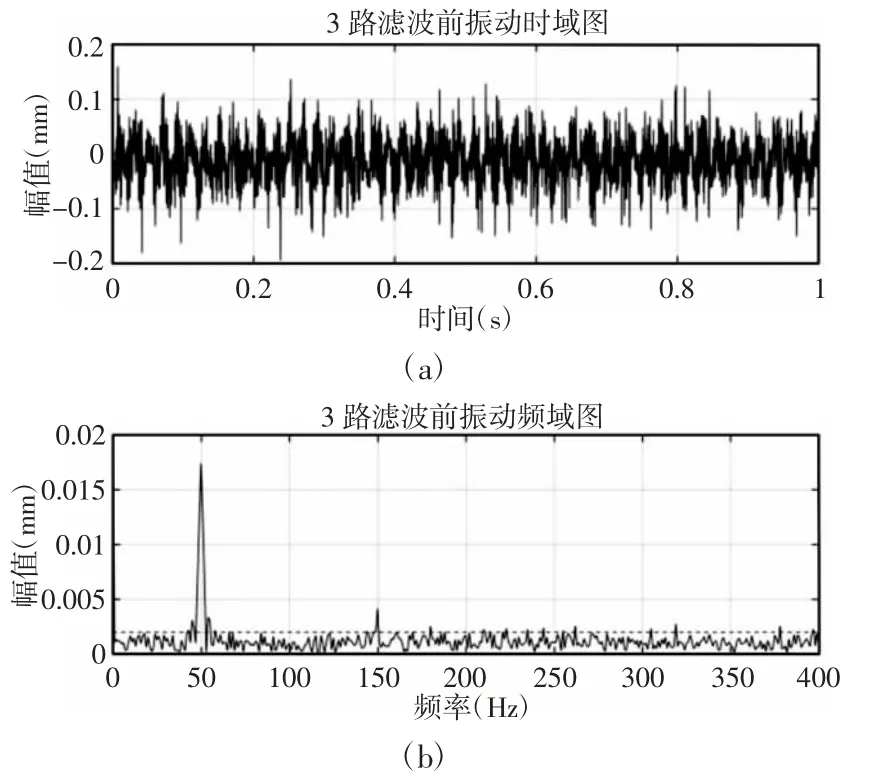
图9 上径向磁轴承振动图(3000r/min)Fig.9 Vibration Diagram of The Upper Radial Magnetic Bearing(3000r/min)

图10 下径向磁轴承振动图(3000r/min)Fig.10 Vibration Diagram of The Lower Radial Magnetic Bearing(3000r/min)
转子转速为3000r/min 时的上下径向磁轴承振动时域图和频域图,如图9~图10 所示。由图9 的频域图中可以看出转子在该转速下主要受到50Hz 的一个信号激励,该频率与转速同频,是转子不平衡量引起的,与上节图3(d)中的仿真结果吻合。此外,转子在50Hz 附近,150Hz 下都出现了小的连续谱,由上节分析可知44Hz 附近是转子平动固有频率,150Hz 是转子不平衡量的3 倍频,这些信号激励可以通过控制系统[10]减小其振动幅值,试验数据中看出这些幅值被控制在0.002mm 上下,表明控制效果良好。同理,转子转速6000r/min 时的上下径向磁轴承振动时域图和频域图,如图11~图12 所示。转子不平衡量100Hz 引起的振动幅值与图3(d)中的仿真结果吻合,倍频200Hz,300Hz 以及平动固有频率44Hz 下的幅值在0.002mm 上下。此外,在同一转速下,下磁轴承转子不平衡响应振动要比上磁轴承转子幅度大,经过对结构分析发现,飞轮转子系统轴向支承位置位于质心上方,下径向轴心距离支承轴向支承位置更远,这就造成上述现象。
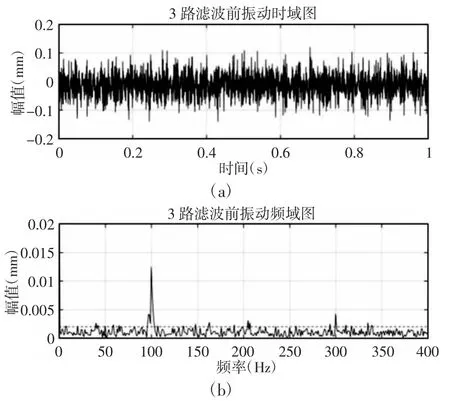
图11 上径向磁轴承振动图(6000r/min)Fig.11 Vibration Diagram of The Upper Radial Magnetic Bearing(6000 r/min)

图12 下径向磁轴承振动图(6000r/min)Fig.12 Vibration Diagram of The Lower Radial Magnetic Bearing(6000r/min)
5 结论
(1)刚性转子有两阶固有频率,其中一阶临界转速下的振型为平动,二阶临界转速的振型为倾斜运动。而基础的模态振型顺序与转子相反,先发生倾斜,后发生平动。
(2)定转子在平动和倾斜运动过程中会受到转子固有频率,定子固有频率,不平衡量三个主要激励。
(3)除转子不平衡量外,定转子固有频率分量受飞轮转速影响较明显,而定子平动对转子平动没有明显影响,倾斜特性却对转子倾斜振动影响明显。
(4)基础的径向支撑刚度影响着转子的径向振动响应,其中对于转子倾斜运动幅值的影响更为明显。
