基于Morris筛选法的SWMM参数敏感性分析

2021-04-02张伟，张江，张曼

江苏水利 2021年3期

张伟，张江，张曼

(1.睢宁县水务局，江苏徐州 221000； 2.徐州市黄河北闸管理处，江苏徐州 221000)

随着城市化进程的快速推进，城市地区发生内涝的概率越来越大，发生的范围越来越广，内涝持续时间及积水深度也越来越长。据调查，2008—2010年在全国349个调查样本城市中，有289个城市发生了内涝，占比80%。北京2012年7月21号特大洪水，造成受灾人口高达160.2万人，116.4亿元直接经济损失；上海市2013年10月7—8日，受强台风影响，全市平均降水量高达152.9 mm，造成全市大范围内涝[1-2]。可见，洪水内涝问题给城市造成了巨大的财产损失和人员伤亡。暴雨管理模型(storm water management model，以下简称SWMM)能够动态模拟城市地区遭遇不同重现期暴雨时内涝发生的时间、地点、范围，在城市地区内涝管理和控制中起了很大作用[3-4]。

SWMM模拟机理主要是根据地形地貌将研究区分为各个子流域，其径流模块将该研究区所发生的降水等进行处理，汇流模块通过管道、河道、水泵、水闸等进行水量、污染负荷输送。用户只需将基础资料输入模型，就可以得到各相关断面的污染工程线及流量过程线。在这一过程中，进行模型的参数率定是非常关键的，参数的变化对模拟结果影响非常大，因此有必要对模型参数进行分析，识别出敏感参数和非敏感参数[5-6]。根据参数敏感性分析结果，需要对敏感性参数取精确值，非敏感参数取经验值即可，这样既可以提高模型参数取值的效率，又能提高模型的精确度。近年来，随着SWMM模型用户的增多，很多学者都对模型的敏感度进行了研究，不同研究方法也得到了不同的结果。本文在前期学者研究成果的基础上，采用应用最为广泛的Morris筛选法，以江苏省徐州市某小区为例，研究SWMM模型的敏感性，为模型率定提供参考。

1 案例研究

1.1 模型建立及参数设置

本次以江苏省徐州市某成熟小区为研究区域，研究区面积约5 hm2，其中透水面积占40%，不透水面积占60%。根据该研究区地下管线资料，结合该区域地形条件，将该研究区概化为雨水管线70条，检查井65个，出水口3个。根据管线和检查井的汇水范围，基于泰森多边形法，该研究区概化为69个集水区。该研究区经SWMM模型概化后具体情况见图1所示。

图1 研究区域概化图

SWMM模型设置参数的原则如下：

不透水面积：根据研究区土地利用情况确定，可通过实地测量确定准确值；稳定下渗率：查《江苏省暴雨洪水查算图表》，并按照徐州市土壤下垫面条件取值；最大下渗率：根据SWMM模型手册及徐州市土壤类型取值，具体与土壤种类、含水量和植被覆盖率有关；入渗衰减系数：主要指霍顿曲线入渗衰减系数，具体指土壤浸水达到饱和状态，到土壤处于干燥状态所需要的时间，一般取值为2～14 d；渗透性洼地蓄水/不渗透性洼地蓄水：主要指降水的初始损失，即植被截留、洼地蓄水等损失；渗透性/不渗透性粗糙系数：根据SWMM模型手册取经验值；坡度：根据徐州市地形资料取值。

SWMM模型中主要参数取值，见表1。

表1 SWMM模型主要参数取值范围

1.2 设计暴雨过程

研究区的涝水主要来源于降水。综合考虑徐州市近几年降雨特性，取暴雨控制时段最大24 h，统计时段选择1 h、3 h、6 h、12 h、24 h 5个时段。以当地代表雨量站降水资料为基础，以《江苏省暴雨洪水图集》可查的点面折减系数，采用同频率法可得暴雨时程分配过程，不同重现期的设计雨型见图2～4。

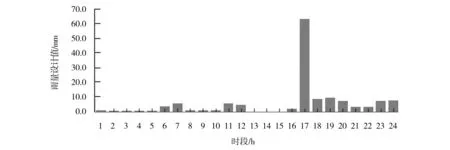
图2 10年一遇典型暴雨过程

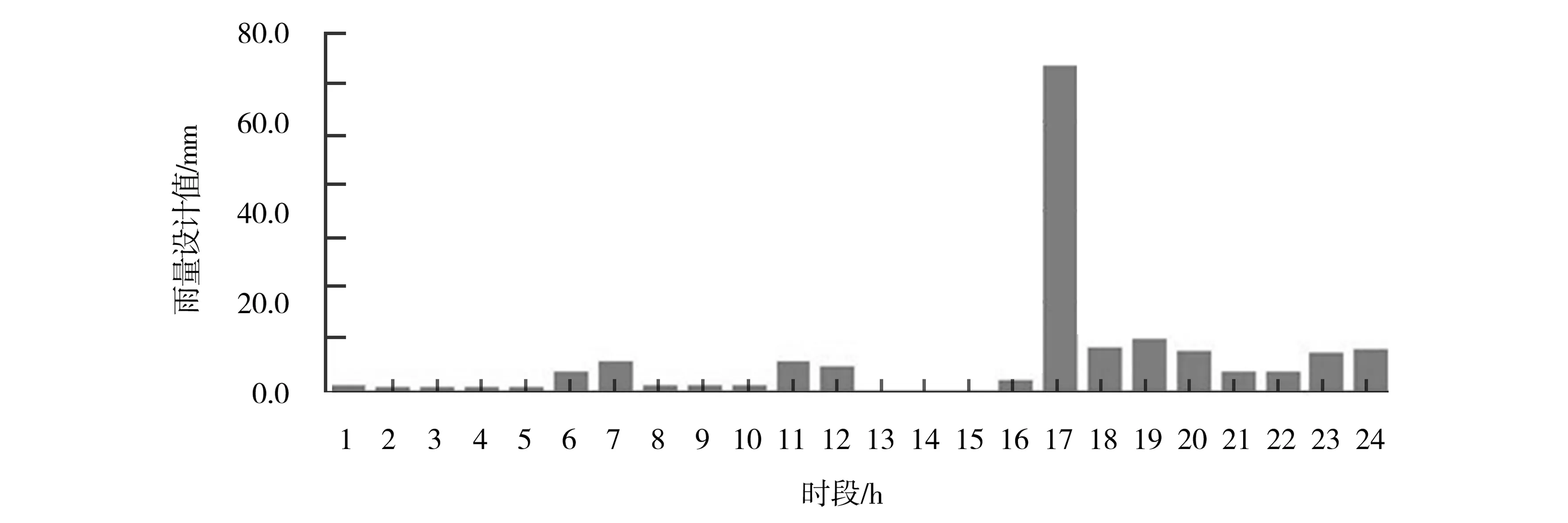
图3 20年一遇典型暴雨过程

图4 50年一遇典型暴雨过程

1.3 基于Morris的敏感性分析法

Morris筛选法具体步骤为：(1)从若干个变量中先选定一个变量xi；(2)在变量xi取值上下随机浮动若干百分比；(3)运用Morris模型得到不同取值xi对应的函数y(x)=y(x1，x2，…，xn)；(4)运用影响值系数ei判断变量xi取值变化对模型运行结果的影响[7]。

ei=(y*-y)/Δi

(1)

式中：y为变量xi变化之前的运行结果；y*为变量xi变化之后的运行结果；Δi为变量xi的变化幅度。

考虑到Morris筛选法在变量xi取值浮动上的随机性影响运行结果，本次研究选用修正的Morris筛选法，即变量xi以固定步长百分率改变，敏感性值可取多个Morris系数的平均值，即，

(2)

式中：SN为变量敏感性判别系数；Yi为Morris模型第i次输出值；Yi+1为Morris模型第i+1次输出值；Y0为变量按照固定步长百分率调整后模型运行结果；Pi为模型经第i次运行后，变量对于初始变量的变化率；Pi+1为模型经第i+1次运行后，变量对于初始变量的变化率；n为Morris模型的运行次数。

根据变量的SN值，修正的Morris筛选法将参数的敏感性划分为4种[8]： (1) 若|SN|≥1，则为高敏感参数；(2)若0.2≤|SN|<1，则为敏感参数；(3)若0.05≤|SN|<0.2，则为中等敏感参数；(4)若0≤|SN|<0.05，则为不敏感参数。

本次根据研究区实际情况，选取稳定下渗率、曼宁宽度等11个变量进行敏感性分析，每个参数的固定步长百分率变化值为-30%、-20%、-10%、10%、20%、30%，主要分析研究区遭遇设计暴雨过程10年一遇、20年一遇和50年一遇时，参数对研究区径流系数和洪峰流量的敏感性。

2 结果分析

根据Morris筛选法，对11个参数按照固定步长改变后，模型运行结果进行分析，分析参数对径流系数的敏感性，具体分析结果见表2。

表2 参数的变化对研究区径流系数的敏感性排序

模型运行结果显示，对10年一遇、20年一遇、50年一遇3种降雨过程，选取的11个参数敏感性差别较小，但是暴雨设计年限越小，参数的敏感性越高，即10年一遇设计降雨过程参数的敏感性高于20年一遇，20年一遇设计降雨过程参数的敏感性高于50年一遇，3种降雨强度下参数敏感性排序一致。不渗透性敏感性最高，最小渗入速率居第二位，漫流宽度居第三位，三者均是中等敏感度参数，其余8个参数的敏感性较差。

根据Morris筛选法，对11个参数按照固定步长改变后，模型运行结果进行分析，分析参数对洪峰流量的敏感性，具体分析结果见表3。

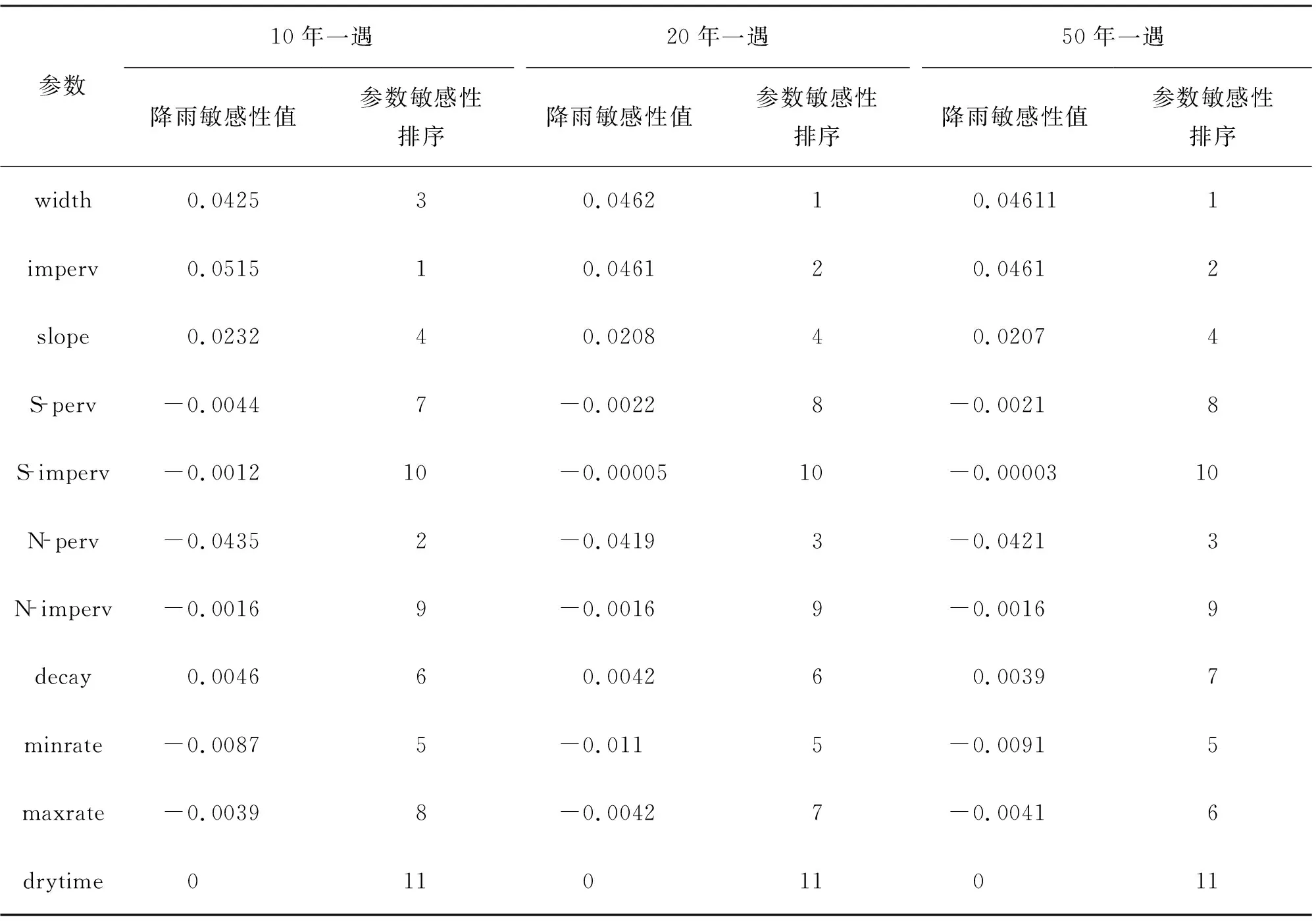
表3 参数的变化对研究区洪峰流量的敏感性排序

模型运行结果显示，对10年一遇、20年一遇、50年一遇3种降雨过程，选取的11个参数敏感性差别较小，但对不同的设计暴雨过程，参数的敏感性排序有细微差别。10年一遇设计暴雨过程，参数敏感性相对较大的是不渗透性、渗透性粗糙系数、漫流宽度；20年一遇设计暴雨过程，参数敏感性相对较大的是漫流宽度、不渗透性、渗透性粗糙系数；50年一遇设计暴雨过程，参数敏感性相对较大的漫流宽度、不渗透性、渗透性粗糙系数。干燥时间为最不敏感参数，它的变化对洪峰流量完全没有影响。