基于摄影测量的盾构隧道轮廓快速检测方法

沈 恺，张 森，李胜腾，刘 劼，郭永发，薛亚东

(1.浙江科技学院 土木与建筑工程学院，浙江 杭州310023；2.同济大学 地下建筑与工程系， 上海 200092；3.中建长江建设投资有限公司，四川 成都 610212；4.中铁二院昆明勘察设计研究院有限责任公司，云南 昆明 650000；5.中国铁路昆明局集团有限公司，云南 昆明 650000)

目前中国隧道建设迅速发展，大量隧道建成并投入运营使用。随着服役时间增加，隧道结构不可避免地出现变形、裂缝及渗漏等病害，不仅影响结构耐久性，还严重危害结构安全性。国内外相关事故层出不穷，隧道安全问题日益突出，隧道检测任务日益紧迫[1-2]。

城际高铁隧道如京张高铁清华园隧道[3]，京沈高铁望京隧道[4]等均使用盾构法修建。在隧道运营期间，列车振动荷载、邻近建筑施工、地层不均匀沉降、地下水位起伏等均可能使其产生较大变形[5]。准确及时的变形检测可及时发现隧道中较薄弱区域，从而有针对性地对隧道结构进行加固修复，对于保障轨道交通运营安全具有重要意义。断面变形是隧道检测中的重要内容，传统检测手段主要包括以收敛仪为代表的接触式测量方法以及以全站仪为代表的非接触式测量方法。收敛仪由于测线数量等限制，通常可获取数据较少。全站仪虽具有较高精度，但现场操作耗时费力、自动化程度较低。此外随着高铁运营时间延长，检测时间被进一步压缩。检测效率较低、效果较差的传统手段已难以适应当下的新形势，因此迫切需要一种准确、快速、经济的隧道断面检测方法。

国内外学者开展了广泛而深入的研究，主要内容集中在以下几方面：①三维激光扫描。具有测量速度快、精度高、覆盖面广等[6]优点，但存在数据量大、设备昂贵、后处理复杂等问题[7]。②机器学习。利用传统的机器学习方法如支持向量机等进行变形计算，但通常模型的泛化性能较差[8]。③深度学习。利用新兴的深度学习技术如卷积神经网络进行裂缝、渗漏水的自动识别与定位，检测效果良好，但其对软硬件均有较高要求[9]。④超声波。Xu等[10]研究了利用超声波进行隧道变形的非接触式测量，详细分析了误差影响因素。⑤近景摄影测量。具有强大的信息快速采集能力，可有效减少外业作业时间，较适用于检测时间紧迫的隧道工程，随着数码技术的不断发展其得到了越来越多研究人员的关注[11]。

周奇才等[12]设计了一种车载分布式激光测距装置，可对隧道内壁进行连续测量并拟合断面轮廓，但其在每个测点均需固定并旋转激光测距仪，难以实现快速移动式测量；郭一诗[13]利用多个工业相机同步拍摄激光光带，采用高速图像拼接技术实现隧道断面实时获取，但其存在难以采集全断面、依赖人工标定、硬件要求较高等问题；朱郭勤[14]设计并建立了室外三维控制场，基于DLT(Direct Linear Translation)方法把后方交会-前方交会交替迭代计算模型应用于工程实践中，计算精度达到1 mm，但对于高精度控制场的需求使其难以有效应用在盾构隧道中；陈振华等[15]设计了一种可提供控制点的活动式金属架，使用非量测数码相机对区间隧道拍照并基于DLT方程解算，验证了DLT方法应用于盾构隧道中的可行性。但其在每个测点均需固定并拍摄左右两张图像，增加了实现快速移动式检测的难度。并且其基于管片拼缝交点进行椭圆拟合得到隧道断面的方法，无法反映断面的真实形态。Ai等[16]利用多个CCD相机图像拼合技术测量隧道断面，制造了相关检测装置，实现了速度5 km/h的移动式断面检测，但最大误差达20 mm，只能适用于检测大变形情况。

虽然摄影测量在隧道检测中的应用研究已取得一定进展，但仍难以实现兼顾高速性、准确性、经济性的移动式测量。本文提出了一种基于DLT理论的隧道断面快速检测方法，建立了使用非量测相机进行快速移动式隧道断面检测的完整操作流程，根据相关原理设计制造了测量系统MTPM-1，进行多次现场试验采集数据并分析结果，充分验证了其具有较强的可行性与良好的准确性，为隧道断面检测提供了一种新的手段。

1 检测原理及系统设计

1.1 DLT方程

非量测相机相比量测相机具有价格低、便携性好等优点，但存在内外方位元素不稳定等问题。DLT直接线性变换方法基于摄影测量核心的共线方程直接建立了世界坐标与像素坐标的转换方程，通过一点的像素坐标直接计算其对应的世界坐标，无需内外方位元素初始定向等过程，较适用于非量测相机的摄影测量解析。由于DLT不需要高精度三维控制场进行准确的相机标定，因此也较适用于高铁盾构隧道处于运营期的工程测量。

3D-DLT在本课题组之前的研究[17]中已有所应用，其方程为

(1)

由式(1)变形可得

(2)

式中：Xwi，Ywi，Zwi分别为三维世界中某点i的世界坐标对应的三个分量；[ui，vi]分别为该点i在二维图像中对应点像素坐标的两个分量；[mi]矩阵包含11个未知系数，均为内外方位元素某种形式的函数。

DLT计算流程为：①在三维空间内设置若干世界坐标可测得的控制点，同时设置若干世界坐标待求的目标点；②使用非量测数码相机拍摄该三维空间，保证控制点与目标点均在镜头成像范围内；③在所摄二维图像中分别提取出原空间中控制点、目标点所对应像素点的像素坐标；④基于式(2)由控制点数据建立方程组解算[mi]矩阵。[mi]矩阵是表明相机内外参数区别的矩阵，受相机分辨率及测量环境等因素影响。由于每个控制点最多提供两个方程，故最少需6个控制点可解共11个mi未知系数；⑤基于式(1)由目标点数据建立方程组解算目标点的Xwi，Ywi，Zwi坐标。由于单张图像对于每个目标点仅提供ui，vi两个已知值，而每点待求世界坐标共三个值，因此在每一个测量断面至少需拍摄两张不同图像，才能提供至少三个方程以求解三个未知坐标。

因高铁盾构隧道为超长线状结构，本文采用“断面2D形态+断面所在里程”的方法代替“隧道三维绝对世界坐标”，因此可合理地舍弃Z轴而使用2D-DLT方程，并使用相对世界坐标代替绝对世界坐标。2D-DLT方程为

(3)

由式(3)变形可得

(4)

相对3D-DLT其具有三点优势：①mi未知系数减少至8个，所需最少控制点减少至4个，布点成本下降；②计算目标点世界坐标时未知量减少至2个，在每一个测量断面仅需单张图像即可求解，无需多相机同步工作以及同名图像匹配，易于实现快速移动式检测；③Z坐标系统误差、偶然误差消失，测量精度得以提高。

1.2 测量系统MTPM-1

目前基于DLT算法的隧道轮廓测量存在的主要问题是在衬砌上布设控制点与目标点较困难。在过去的研究中，布设控制点的方法主要是通过在隧道内壁上贴设反光片，利用全站仪测出这些反光片的绝对坐标作为控制点；或是通过放置一个黑白相间网格的标定板，以网格交点作为控制点，这些控制点坐标为相对坐标。贴反光片的方法测量精度较高，但只能测得少量断面，并且贴设反光片的工作量较大，耗时较长，不太适用于高铁盾构隧道检测；设置标定板的方法由于标定板在尺寸上通常远小于隧道断面，通过外延插值的方法计算得到的断面轮廓误差往往较大。

为解决布点问题，本文提出分别利用激光测距仪与线状激光发射器布设控制点与目标点，并建立基于该布点方法的完整测量系统MTPM-1[17]。

具体的布点方法为：线状激光发射器在衬砌内壁上投射出红色圆弧形轮廓线，构成目标点集；通过三向调节使激光测距仪与圆弧形轮廓线共面，即激光测距仪在平面内旋转时测距光斑沿轮廓线移动，测距光斑构成控制点集；在激光测距仪旋转过程中，各设备相对位置固定，所摄图像中唯一变化的即控制点(测距光斑)位置，包含完整圆弧形轮廓线以及单个控制点的图像。该方法具有布点量大、点位灵活、布点成本低、操作简便等特点。

为实现快速移动式检测，在特定工程应用时具体操作分为两部分：首先利用旋转单激光测距仪的方法确定最优图像分辨率、最优控制点数量与最优控制点分布形态；其次以最优分布形态安装与最优控制点数量同等数量的激光测距仪或使用多激光测距头，使其同时工作提供多个控制点，实现隧道断面快速移动式检测。在不同内径、不同形态隧道中使用测量系统MTPM-1的操作步骤为：①在隧道区间内某待测断面固定移动模块与拍摄模块；②通电使线状激光发射器在隧道衬砌内壁上投射出圆弧形轮廓线，调整线状激光发射器空间姿态使圆弧形轮廓线垂直于隧道纵向；③通电使激光测距仪发射测距光斑，调整激光测距仪空间姿态使测距光斑在激光测距仪旋转过程中始终保持在圆弧姿态使测距光斑在激光测距仪旋转过程中始终保持在圆弧；④激光测距仪归于水平位置，角度置零，通过马达控制激光测距仪以某固定角度旋转若干次，每旋转一 次拍摄一张图像并记录测距数据与对应角度，此时测距光斑在图像中构成一个控制点，总旋转次数达到一定值后反向旋转激光测距仪回到零度位置；⑤通过马达控制激光测距仪以较缓慢的转速连续旋转并连卖测距，连续记录测距数据与对应角度，总旋转角度达到一定值后停止，以之拟合断面真实形态衡量DLT结果精度；⑥将原始图像压缩为不同分辨率的图像，每次选取不同分辨率图像进行DLT拟合，比较DLT拟合结果与断面真实形态的误差确定最优图像分辨率，将所有图像压缩为最优分辨率大小；⑦依次选取不同数量控制点进行DLT拟合，比较DLT拟合结果与断面真实形态的误差，确定最优控制点数量；⑧依次选取不同分布形态控制点进行DLT拟合， 比较DLT拟合结果与断面真实形态的误差，确定最优控制点分布形态；⑨以最优分布形态安装与最优控制点数量同等数量的激光则距仪，使其同时工作，每个测量断面仅需拍摄一张图象，实现隧道断面移动式快速检测。

本文所用设备的关键参数为：尼康D7000型数码单反相机，其具有1 608万像素(4 928×3 264像素)APS-C(Advanced Photo System Type-C)画幅感光元件；图丽ATX PRO DX 11～16 mmⅡ超广角变焦镜头，等效全画幅焦距为16～24 mm，对角线视角为84°～104°，本文均使用11 mm端拍摄；激光测距仪为HZH-B40+型，测距精度为1.0 mm±20 ppm，5 m距离时光斑直径约4 mm，激光波长为620～690 mm，为Ⅱ类安全激光。

1.3 畸变校正

非量测相机的显著缺点是镜头存在较大畸变,尤其是超广角镜头通常存在较严重的桶状畸变。若不进行畸变校正，测量结果必然存在较大误差。利用Matlab软件中的Calib标定工具进行镜头畸变校正。首先从不同角度对标准标定板拍摄若干张图像，见图1。通过Calib工具标定后得到一组畸变参数，对新输入的图像加载该参数可输出畸变校正后的图像。图1中第一张标定板图像校正后见图2，可发现畸变得到了较好消除(画面边缘处尤为明显)。标定结果显示横、纵轴最大像素偏差分别约为0.8 像素与0.9 像素，对应实际测量误差约为1 mm，认为该畸变已在隧道工程测量可接受范围内。此外可采用平差理论、计算机视觉、机器学习等技术进一步提高畸变校正精度[18]。

图1 畸变校正前图像

图2 畸变校正后图像

2 盾构隧道轮廓检测

2.1 现场检测

按照MTPM-1的操作步骤，在某隧道区间内进行了若干次现场试验。试验中，设置激光测距仪每次旋转5°，共旋转36次并拍摄37张图像，获得37个控制点。拍摄完成后设置激光测距仪反向旋转回到零度位置，以1(°)/s的速度连续旋转180°，测距频率设为1 Hz，共记录180个测距值。为校验测量装置的精度，同时采用全站仪进行了隧道轮廓测量。测量所用相机镜头均使用11 mm焦距，拍摄距离约为6 m。

2.2 数据处理

采用摄像建立测量控制点，根据控制点采用DLT算法计算所测隧道轮廓，其测量精度与图像分辨率、控制点数量以及控制点分布形态等有关，这里采用控制变量的方法研究其影响规律。下面选取实测隧道任一断面进行分析以分析其一般性规律。

具体操作流程为：

(1)将拍摄的37张图像导入Photoshop中进行最大值堆栈操作，最大值堆栈原理是对每一像素取所有堆栈图像中最大值后输出一张图像。现场拍摄的每一张图像均包含一个测距仪激光亮点，因此所输出的是一张包含37个控制点的图像，见图3。

图3 最大值堆栈图像(图中数字为标记点编号)

(2)利用Matlab基于颜色差异提取出圆弧形轮廓线上所有点的像素坐标，构成目标点像素坐标集。由于隧道内管线、底板的遮挡，不免有个别点位发生偏移。为避免其对椭圆拟合产生影响，需对图像进行预处理，避免其被提取为目标点。

(3)基于亮度差异提取出圆弧形轮廓线上最明亮点的像素坐标，构成控制点像素坐标集。

(4)根据激光测距仪测得控制点距旋转中心的真实距离D，以及由控制电机记录对应的旋转角度θ，计算控制点相对世界坐标，表达式为

x=-D·cos(θ·π/180°)

(5)

y=D·sin(θ·π/180°)

y=D·sin(θ·π/180°)

(6)

(5)通过式(4)解算[mi]矩阵，再利用式(3)循环计算目标点相对世界坐标。大量相对世界坐标拟合出断面真实形态与尺寸，获得基于DLT计算的拟合结果。

(6)利用激光测距仪缓慢匀速旋转180°记录的180个测距值计算相对世界坐标，以此拟合真实断面形态。

(7)对DLT拟合得到的大量坐标点进行椭圆拟合，以椭圆拟合的长轴、短轴、椭圆中心x/y坐标、绕x轴(长轴)旋转角共五个参数作为误差衡量指标。因隧道断面在荷载作用下通常呈现“扁鸭蛋状”变形，故进行椭圆拟合具有较好的合理性。此处进行椭圆拟合的目的主要是进行精度分析，在后续实现移动式快速测量时无需进行拟合处理。此外，由于绕x轴旋转角与相机水平角度、激光测距仪零度位置、隧道水平角度等均相关，而这些因素较难控制，因此其绝对值仅供参考，而相对差值可作为误差衡量指标。另外由于隧道内局部管线、轨道底板等的遮挡，圆弧形轮廓线上或缓慢扫描过程中不可避免存在个别点位发生偏移的情况。为避免这些偏移点对椭圆拟合的影响，需对图像进行人工预处理，避免噪声被错误提取为目标点。

(8)依次选取不同图像分辨率、不同数量控制点与不同分布形态控制点进行DLT拟合，根据各工况下误差情况确定最优图像分辨率、最优控制点数量与最优控制点分布形态。

(9)当最优图像分辨率、最优控制点数量与最优控制点分布形态确定后，以最优分布形态安装固定与最优控制点数量同等数量的激光测距仪，使其同时测距提供控制点，无需再进行旋转操作，并且由于采用2D-DLT方程，每个测量断面仅需拍摄一张图像，实现移动式隧道断面测量。

测量断面的真实形态与DLT计算拟合结果见图4，其中红色轮廓为真实断面椭圆拟合，蓝色轮廓线为DLT椭圆拟合，可以发现两者轮廓十分吻合。此时计算得到的旋转中心像素坐标(2 196,2 649)，经检验与图4中转轴中心位置一致，说明了计算的正确性。

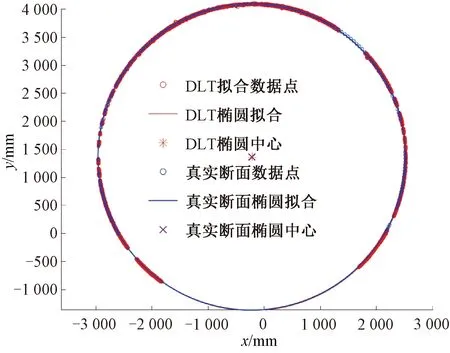
图4 DLT拟合结果与断面真实形态

3 测量误差与试验参数分析

在各影响因素中，图像分辨率主要影响测量精度、综合成本与计算时间；控制点数量主要影响测量精度与综合成本；控制点分布形态主要影响测量精度。应采用固定变量的方法，先确定图像分辨率，其次确定控制点数量，最后确定控制点分布形态。

3.1 最优图像分辨率

为探究图像分辨率对DLT拟合精度的影响，畸变矫正后将原始图像(4 928×3 264像素)分别压缩至80%(3 942×2 610像素)，60%(2 957×1 958像素)，40%(1 971×1 305像素)，20%(986×653像素)。采用8个均匀分布控制点，对压缩后的图像分别进行DLT拟合得到一组坐标点，再对坐标点进行椭圆拟合，隧道断面K213+53椭圆拟合结果见表1。

对16个隧道断面总计160组拟合数据进行统计分析，随图像分辨率减小，长短轴绝对误差逐渐增大，见图5。由图5、表1可知，图像分辨率越大，单张图像计算时间越长，对存储空间、传输速度、计算性能等硬件要求越高。高分辨率设备价格往往较昂贵，因此需综合考虑设备成本、精度要求、计算时间确定最优图像分辨率。

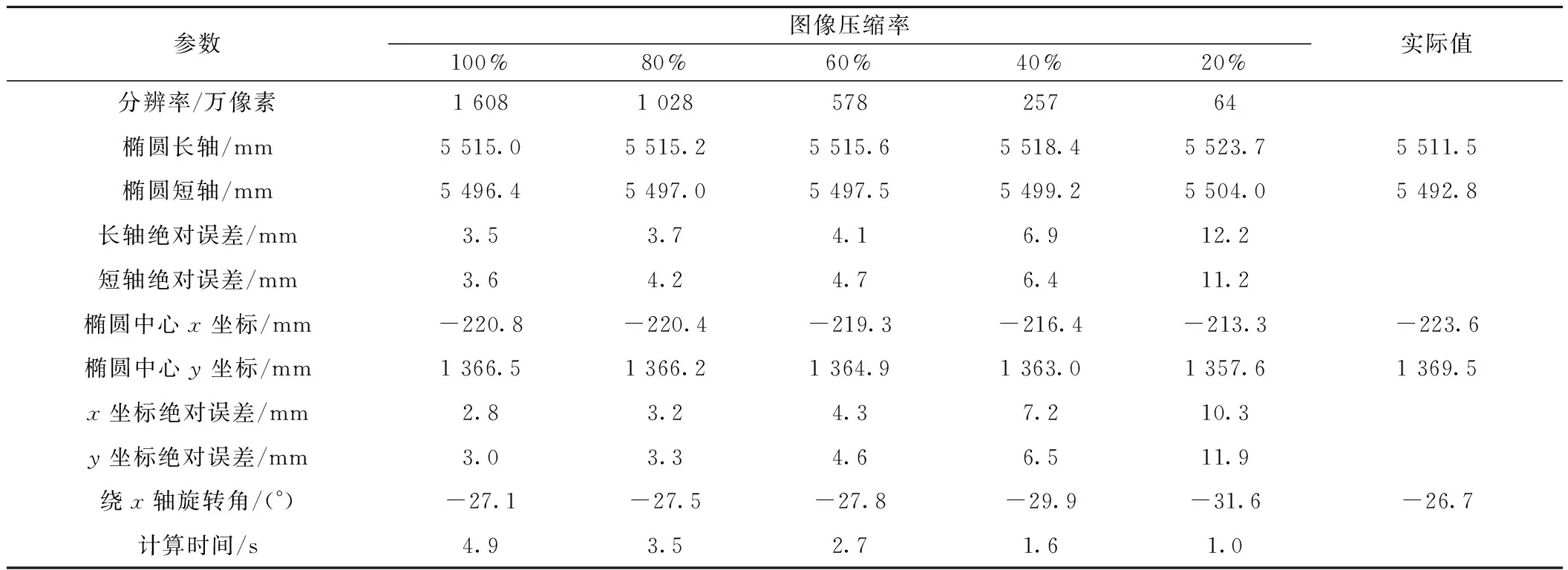
表1 K213+53不同图像分辨率椭圆拟合结果(8个均布控制点)

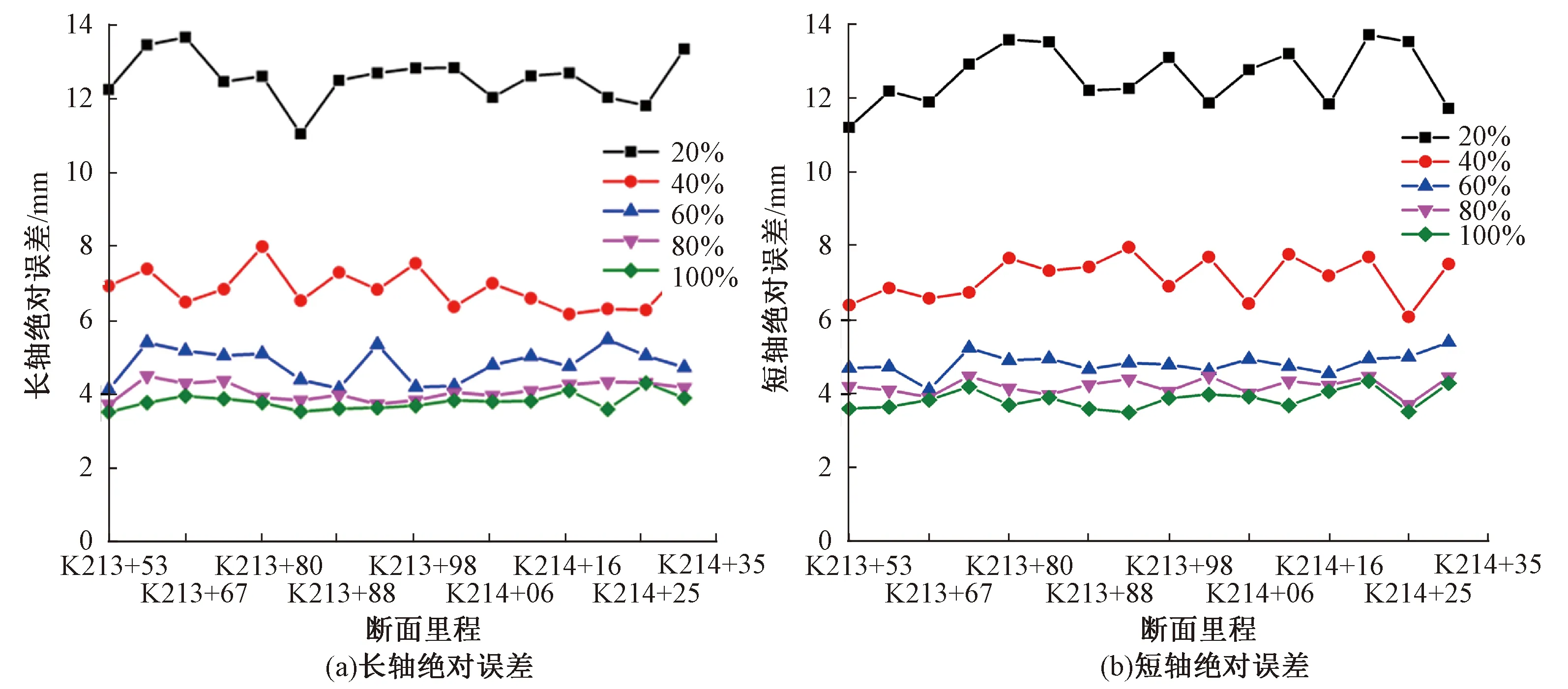
图5 不同图像分辨率椭圆长短轴绝对误差统计结果(8个均布控制点)

实际工程中，椭圆长短轴收敛值较椭圆中心坐标更能反映出结构变形状态。根据表1及图5，在满足椭圆长短轴绝对误差5 mm以内的条件下，可选择578万像素图像分辨率，可较好地兼顾各方面因素。如果对于测量精度有更高需求，可选择更高图像分辨率。

3.2 最优控制点数量

为探究控制点数量对DLT拟合精度的影响，取图像分辨率为60%，以均布方式依次选取4、8、12、16、20个控制点，分别进行DLT拟合得到一组坐标点，再对坐标点进行椭圆拟合，拟合结果见表2。此时目标点数量、单张图片计算时间均与表1中60%情况相同。

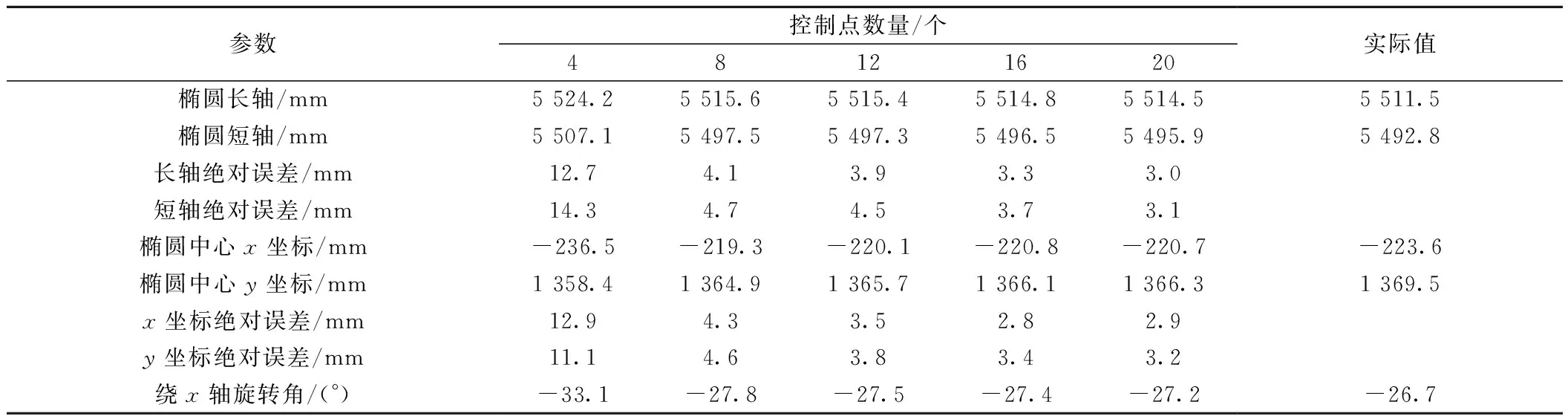
表2 K213+53不同控制点数椭圆拟合结果(图像分辨率60%)

对16个隧道断面总计160组拟合数据进行统计分析，随控制点数量增加，长短轴绝对误差逐渐减小，见图6。当采用4个控制点时，椭圆长轴绝对误差均大于11.5 mm，椭圆短轴绝对误差均大于11 mm，这是由于控制点对于距控制点较远目标点的“控制作用”较弱，当控制点较少时该效应被放大；当采用20个控制点时，长短轴绝对误差降低至3.5 mm左右。此时误差来源主要是仪器系统误差与畸变残余误差。此后即使再增加控制点数量也难以有效提高精度，残余误差基本保持稳定。相对于之前的研究成果[17]，精度有了较明显的提高。针对不同断面盾构隧道，实际应用时应根据具体精度要求确定最优控制点数量。根据本文试验结果，在满足误差小于5 mm的条件下，对于内径5.5 m的盾构隧道，图像分辨率为60%时(2 957×1 958像素)，8个控制点即可满足精度要求。

图6 不同控制点数椭圆长短轴绝对误差统计结果(图像分辨率60%)

图像分辨率与控制点数量共同影响着测量精度：当图像分辨率过低时，即使使用较多的控制点，也无法有效提高测量精度，因为此时制约因素为图像分辨率；当控制点数量过少时，即使使用较高的图像分辨率，也无法有效提高测量精度，因为此时制约因素为控制点数量。如果同时使用较多的控制点与较高的图像分辨率，各方面成本都会显著增加。因此，针对不同断面盾构隧道，实际应用时应根据具体精度要求、成本要求综合确定最优控制点数量与图像分辨率。

3.3 最优控制点分布形态

为探究控制点分布形态对DLT拟合精度的影响，取60%分辨率图像与8个控制点，分别选取均匀分布、左侧集中分布、顶部集中分布和右侧集中分布等四种形式，采用多次随机选点计算误差统计特征，结果见表3。

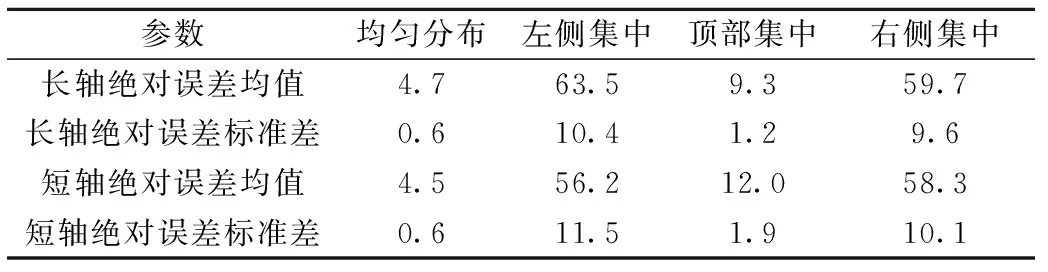
表3 不同分布形态时长/短轴相对误差统计特征(8个控制点) mm

由表3可知，控制点分布形态对测量误差有显著影响。当控制点均匀分布时，椭圆长短轴绝对误差均小于5 mm；当控制点集中分布在顶部时，长轴绝对误差较均布情况略有增加，短轴绝对误差增幅较大，这是因为隧道在荷载作用下通常呈“横鸭蛋”变形。通常横轴为长轴，竖轴为短轴，控制点在顶部集中分布时，对于底部的误差显著放大，因此短轴误差更大，对于长轴的效应没有短轴明显；当控制点集中分布在左、右两侧时，长、短轴绝对误差迅速增加，最大绝对误差均值达约63.5 mm，是均布情况的约13倍。这是由于均布情况下控制点对整体轮廓的“控制作用”分布比较均匀；而当控制点集中分布在某一区域时，控制点对于较远区域的“控制作用”显著降低，因此使测量结果出现较大偏差。因此，在大多数情况下，均匀分布是最优控制点分布形态。

3.4 快速移动式检测

对于内径5.5 m的盾构隧道，根据本文试验结果，当拍摄距离为6 m左右时(使用等效16 mm焦距镜头)，在满足误差5 mm以内的条件下，最优图像分辨率为2 957×1 958像素，最优控制点数量为8个，最优控制点分布形态为均匀分布。在激光测距仪旋转平面内均布安装8个激光测距仪提供8个控制点。使用以上参数在某隧道区间内测量了20个断面，测站间距为5 m，利用滚轮在既有轨道上运行，总测量时间为3 min，平均测量速度约2 km/h，实现了盾构隧道断面快速移动式检测。结果表明本文提出的方法操作简便、测量精度高，且价格低廉，易于在工程应用中推广。

在布置激光测距仪时，应尽量使测距光斑避开管线。由于衬砌管片通常呈连续变形特征，因此距离较近的两个断面一般不会出现显著的形态变化。考虑到隧道实际状况，建议每隔3～5环设置一个测量断面，可与光电编码器配合工作实现每隔一定距离自动采集图像。

3.5 隧道曲线段检测

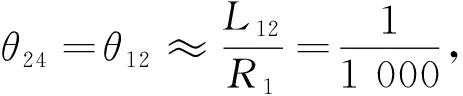
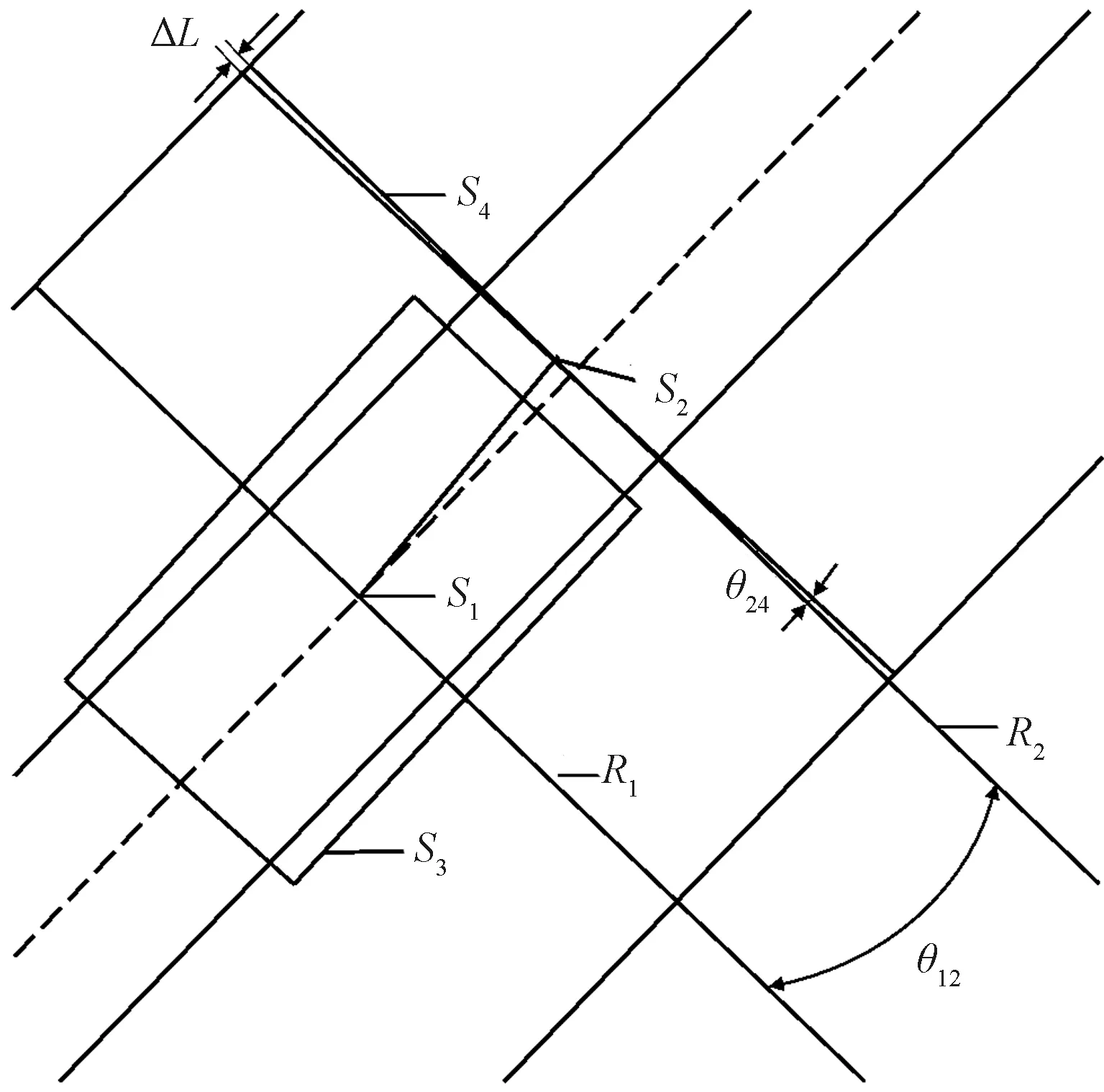
图7 隧道曲线段平面图

4 测量系统优化设计

4.1 拍摄距离优化设计

拍摄距离与镜头焦距、镜头位置、拍摄方向等有关。理论上拍摄距离越远对于设备硬件要求越高，如无线设备等一般有传输距离限制。并且为方便现场工作，通常以拍摄距离较小为宜。

限制拍摄距离的核心因素是需在成像范围内覆盖整个轮廓线，拍摄时隧道侧视图见图8，蓝色线为成像范围边缘，黄色线为镜头主光轴，红色线为轮廓线，需通过合理安排相关设备位置使红色线条包含在蓝色线条内。

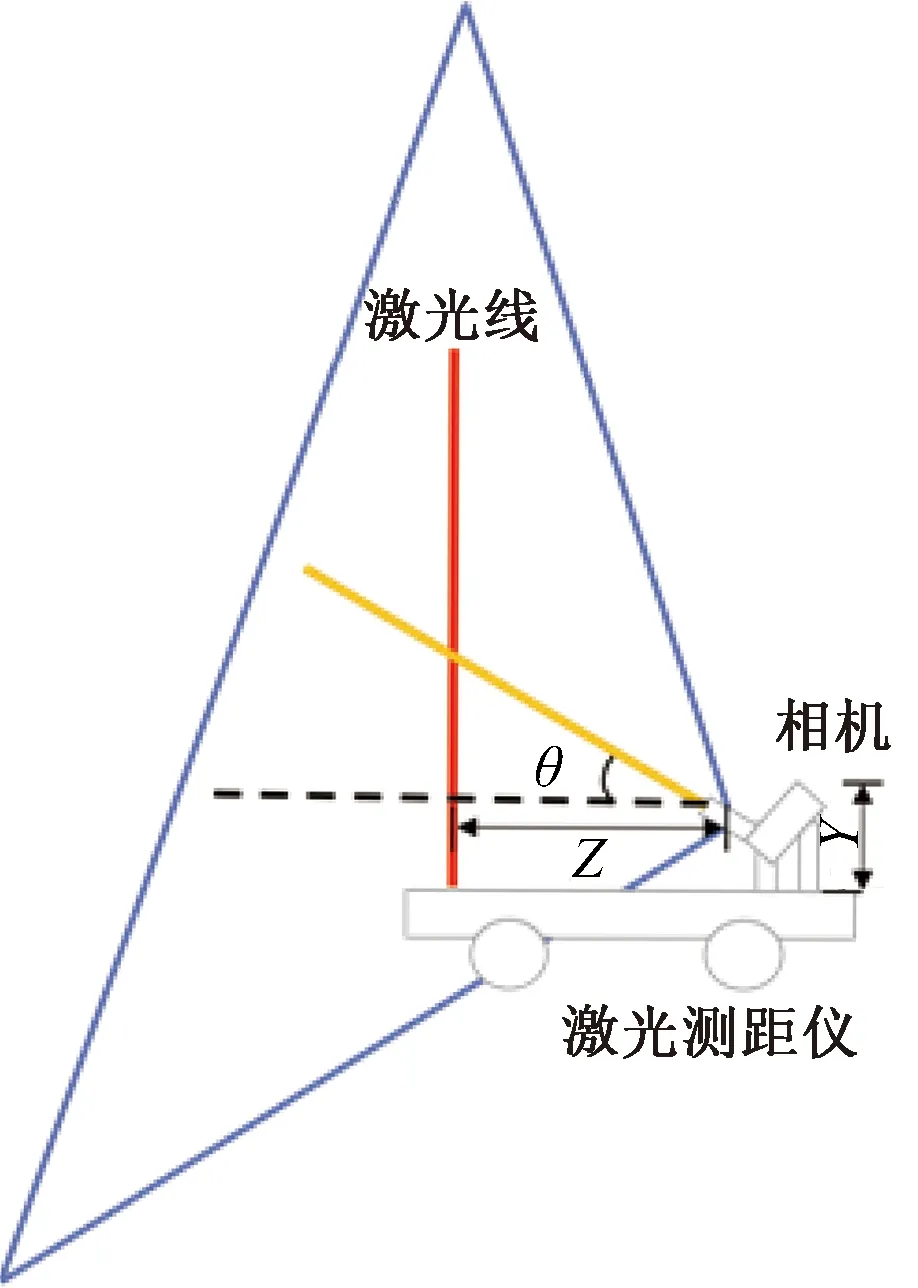
图8 拍摄距离限制原理图

据此可得出4个限制条件：

(1)轮廓线顶部在成像范围内的限制条件，表示为

(1.95-Y)2+Z2-[2.75/tan(θ2·π/360°)]2>0

(7)

式中：Y为相机高度(Y> 0)；Z为拍摄距离；θ为相机仰角；θ1为相机竖向视角；θ2为相机水平视角。

(2)轮廓线底部在成像范围内的限制条件，表示为

Z·tan[(θ1/2-θ)·π/180°]-Y>0

(8)

(3)轮廓线两侧在成像范围内的限制条件,表示为

Z·tan[(θ1/2-θ)·π/180°]+Y-5>0

(9)

(4)轮廓线侧底部45°位置在成像范围为内的限制条件，表示为

(10)

根据上述4个限制条件，可通过Excel优化求解器求解任一焦距下的最小拍摄距离以及对应的相机高度、镜头仰角。

目前全画幅相机非鱼眼最广焦距为10 mm，一般认为超广角焦距在24 mm以内，10～24 mm等效焦距对应的最小拍摄距离、相机高度、镜头仰角参数组合见表4。为验证计算结果正确性，在现场测试了10 mm焦距(老蛙10～18 mm镜头，转换系数为1)、15 mm焦距(尼康AF-P 10～20 mm VR，转换系数为1.5)、21 mm焦距(理光GR2，18 mm镜头，0.75倍广角转换镜，转换系数为1.5)，发现现场测试距离与理论计算距离高度一致，证明了计算结果的准确性。

表4 常见焦距对应的最小参数组合

老蛙10～18 mm的现场测试图见图9，此时拍摄距离约为1.5 m，接近计算结果的1.44 m。由于相机较接近地面，并且仰拍角度较高，因此隧道下部部分结构被遮挡。若将相机高度Y逐渐增大，相机仰角θ逐渐减小，则拍摄距离Z逐渐增大，见图10，此时隧道断面较完整地记录在影像中。

图9 老蛙10～18 mm现场测试图(10 mm焦距、拍摄距离约为1.5 m、较小高度、较大仰角)

图10 老蛙10～18 mm现场测试图(10 mm焦距、拍摄距离约为2 m、较大高度、较小仰角)

综上所述，拍摄距离应综合考虑各项因素后慎重选取。

4.2 鱼眼镜头优化设计

当使用目前最广的非鱼眼超广角焦距时，焦距取10 mm，最小拍摄距离依然在1.5～2.0 m。为使整体系统更加便携，考虑使用具有超大视角(180°以上)的鱼眼镜头，拍摄距离可降低至0.3～0.5 m。

普通光学系统一般遵循物像相似的小孔成像原理且致力于完善这种相似性，但是鱼眼镜头不满足该原理，其是非相似成像。因鱼眼镜头的非线性成像特性，DLT直接线性变换法无法直接应用，后续研究可考虑建立针对鱼眼镜头的空间坐标与图像坐标的映射关系，实现图像与对应轮廓的直接转换。

4.3 双激光优化设计

为提高测量效率，考虑设置双激光同时测距。激光间距可设置为0.5 m或1.0 m，在加倍测量数据的同时，双激光断面还可互相佐证，保证测量结果的可靠性。

因双激光断面可互相提供Z轴(隧道纵向)信息，可双激光联立建立3D-DLT方程进行断面求解。后续应详细研究双激光的应用方法，探究3D-DLT方法与2D-DLT方法的区别，在测量精度、测量效率、操作复杂度等各维度综合比较两者区别。

5 结论

针对DLT算法在城际高铁隧道轮廓检测中布点困难的问题，提出了基于激光的布点方法，利用线状激光发射器投射目标点，利用激光测距仪投射控制点，基于2D-DLT进行摄影测量解析，设计并制造了测量系统MTPM-1。在之前研究的基础上，采用2D-DLT代替了3D-DLT从理论上将最少控制点数量由6个减少到4个。在某隧道区间的现场试验证明了该方法的操作简便性与测量结果的准确性，并进一步探讨了最优分辨率和最佳控制点数量，实际可根据测量需要对相机分辨率及控制点数量进行调整。最终断面拟合误差控制在5 mm以内，基本满足工程测量的需要。该方法具有精度高、检测速度较快、成本低、操作简便等特点，能较好地满足盾构隧道轮廓快速检测的需要。

基于此基础上，对下一代测量系统进行了优化设计，提出了距离优化、镜头优化及激光优化三种优化方案，可为同类设计提供参考。