钢轨磨耗动态测量中轨廓自动配准方法研究

史红梅，张志鹏，李富强

(1.北京交通大学 机械与电子控制工程学院，北京 100044；2.中车青岛四方机车车辆股份有限公司，山东 青岛 266111)

钢轨是支撑列车运行的重要基础设施，列车的高速、重载、高密度运行使钢轨磨耗问题日益突出[1]。钢轨的过度磨损会对列车行车的平稳性、安全性、乘车舒适性以及车辆和轨道各零部件的使用寿命造成极大的危害。高效准确的测量钢轨磨耗，对于确保铁路运营安全至关重要。铁路部门长期以来主要采用专用卡尺，由人工定期进行钢轨磨耗测量，该方式存在检测效率低、检测结果容易受人为因素影响等缺点。

近年来随着计算机视觉技术的高速发展，以图像传感器和结构光为核心，具有高效、可靠等特点的非接触式钢轨磨耗动态测量系统日趋成熟，得到了国内外铁路部门和科研机构的广泛关注与研究。Alippi等[2]提出采用激光摄像技术进行钢轨轮廓的动态测量，利用神经网络技术对结构光带的中心轮廓进行了重建。Popov等[3]建立了结构光传感器标定模型，并成功应用于地铁轨道测量系统。孙军华等[4]提出一种基于结构光的钢轨磨耗快速测量方法，仅依靠轨腰轮廓寻找钢轨磨耗约束点，极大减少了计算量。占栋等[5]对基于激光摄像的钢轨轮廓测量技术进行了系统研究，提出针对车体振动的补偿方法，有效提高了测量精度。Zhou等[6]针对钢轨轮廓测量系统的标定问题，提出一种基于平行运动目标的线结构光标定方法，提高了标定精度。

钢轨磨耗动态测量过程中关键问题之一就是将测量轮廓与标准轮廓配准，进而根据钢轨磨耗的定义计算相关磨耗值。轮廓配准的精度直接影响系统的测量精度。谭周文等[7]将钢轨轨腰圆弧圆心作为基准点进行轮廓配准，为了拟合圆心坐标，以测量数据点的坐标特征进行轮廓分割，但该特征只能适用于固定类型的传感器。占栋等[8]通过设定测量轮廓的曲率阈值实现轨腰、轨底圆弧的自动分割，但实际测量轮廓曲率特征波动明显，难以确定合适的阈值。孙军华等[9]选取轨腰数据集作为基准，采用ICP配准算法计算轨道测量坐标系和标准坐标系之间的转换模型，依靠单一传感器实现了基准测量和磨耗测量，但为提高算法效率，将迭代搜索的区间限制在测量点的局部邻域内，使得迭代算法容易陷入局部最优解。

本文研究了一种基于结构光视觉的钢轨磨耗检测系统，针对磨耗动态测量中关键的轮廓配准问题，首先将轨腰圆弧轮廓的圆心作为基准点，实现测量轮廓与标准轮廓的初步配准，针对测量轨廓圆心拟合提出了基于RDP算法的轨腰圆弧轮廓自动分割方法，然后利用基于KD树的改进最近点迭代算法进一步提高轮廓配准的精度，最终实现测量轨廓与标准轨廓的自动配准。

1 钢轨磨耗测量系统原理与方案

本文研究的钢轨磨耗测量系统安装在如图1(a)所示的手推式轨道检测小车上，可自动连续地实现钢轨磨耗测量与分析，与大型轨检车相比，这种检测方式更加适合铁路的日常维护。为实现结构光图像的采集与传输，设计了如图1(b)所示的结构光视觉传感器，其主要由线激光器与高分辨率面阵CCD相机组成。测量时，线激光器投射出的激光平面与钢轨表面垂直相交，形成包含横截面轮廓信息的结构光光带，CCD相机与结构光平面呈一定夹角采集光带图像，通过以太网传输到上位机。

图1 钢轨磨耗检测系统

钢轨磨耗测量算法流程见图2，首先对结构光系统进行标定，然后对原始图像进行处理，以提取光条中心点的亚像素坐标；然后，利用系统标定参数，将提取的中心点图像坐标转换为相机坐标系下的物理坐标，得到钢轨的测量轮廓；最后，通过轮廓配准，将测量轮廓变换到标准轨道平面坐标系，计算标准轮廓与测量轮廓上磨耗测量点之间的距离，获取磨耗值。

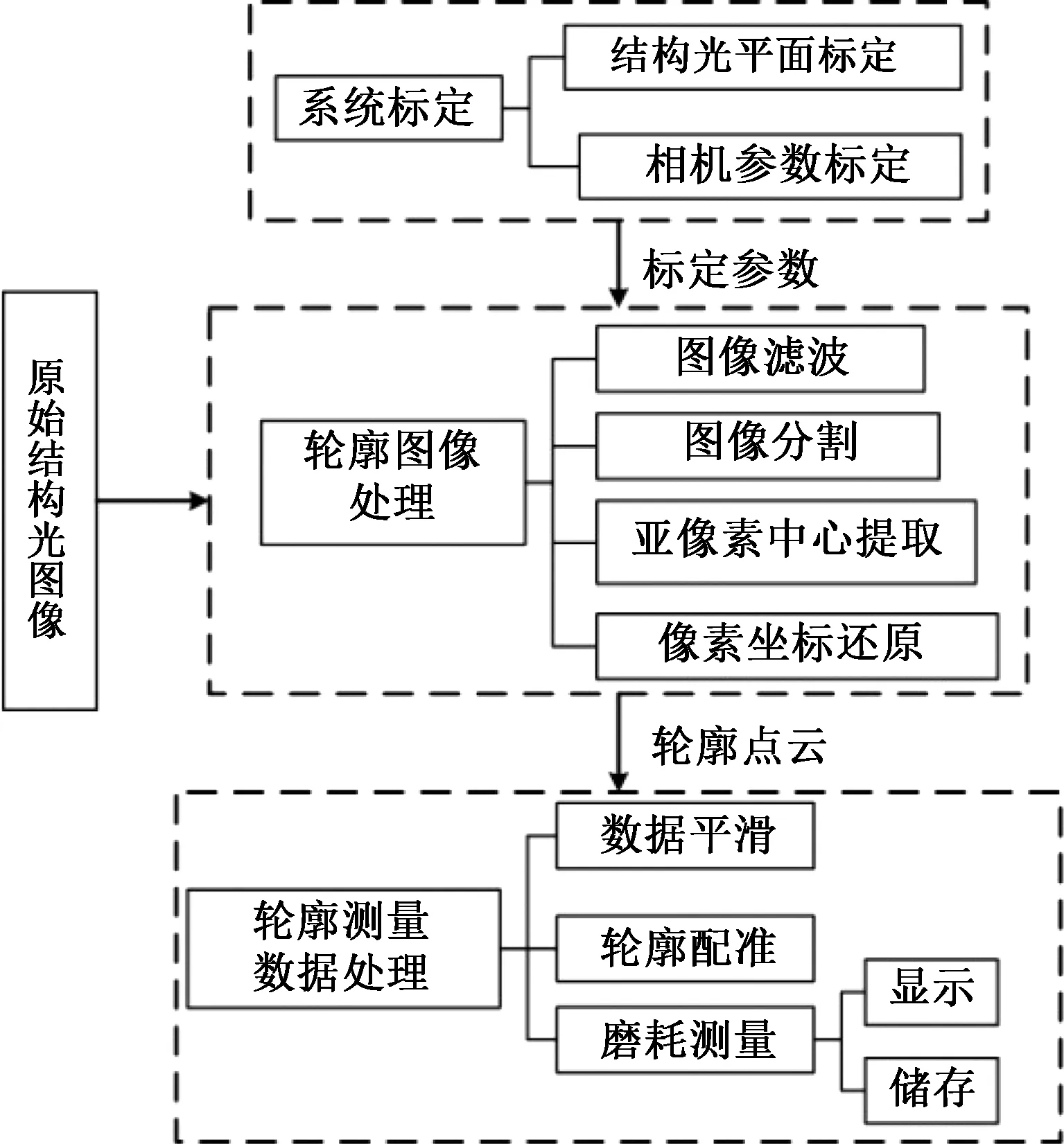
图2 钢轨磨耗测量算法流程

2 钢轨轮廓配准原理

钢轨轮廓配准的原理见图3。根据结构光测量模型可知，测量轨廓位于相机坐标系ox′y′。如图3(b)所示，需要将测量轮廓与标准轮廓进行配准，使其转换到标准轨道平面坐标系oxy，才能与标准轮廓对齐，分别计算钢轨水平磨耗Wh与垂直磨耗Wv。

图3 钢轨轮廓配准原理

钢轨断面轮廓的配准方法主要包括基于基准点配准和基于ICP算法配准两类，其中基准点的配准算法是通过计算任意两组对应基准点的坐标变换矩阵，确定配准关系。该方法配准速度快，但配准精度受基准点的提取精度影响较大，鲁棒性差；ICP算法直接对数据集处理，利用最小二乘优化方法，每次迭代过程中针对源点集中每一个数据点，在目标点集中寻找欧式距离最近的构成对应点对估计变换参数，然后应用于源点集，重复以上步骤，直到满足给定的收敛条件，求得最优的平移和旋转参数，完成配准。该方法配准精度高，但为避免陷入局部最优解，要求待配准点集有较好的初始位置，且配准效率受最近邻点对搜索影响，速度较慢。

本文提出一种两段式配准算法以提高轮廓配准精度和效率。首先利用轨腰圆弧圆心作为基准点实现轮廓的粗配准，然后采用基于KD树的改进ICP算法，以粗配准结果作为迭代初值实现轮廓的精配准。

3 钢轨轮廓配准方法

60 kg/m标准钢轨断面轮廓见图4，oxy为标准轨道平面坐标系。其中AB为半径400 mm的圆弧，BC为半径20 mm的圆弧，CD、EF为斜率1∶3和1∶9的线段，DE为连接CD、EF为半径40 mm的圆弧。钢轨的轨腰、轨底不参与轮廓接触，形变小，且该部分轮廓几何信息丰富，容易提取特征，因此轨廓的初始配准选择轨腰圆弧AB、BC的圆心作为基准点，精配准选择该部分轮廓作为配准点集。

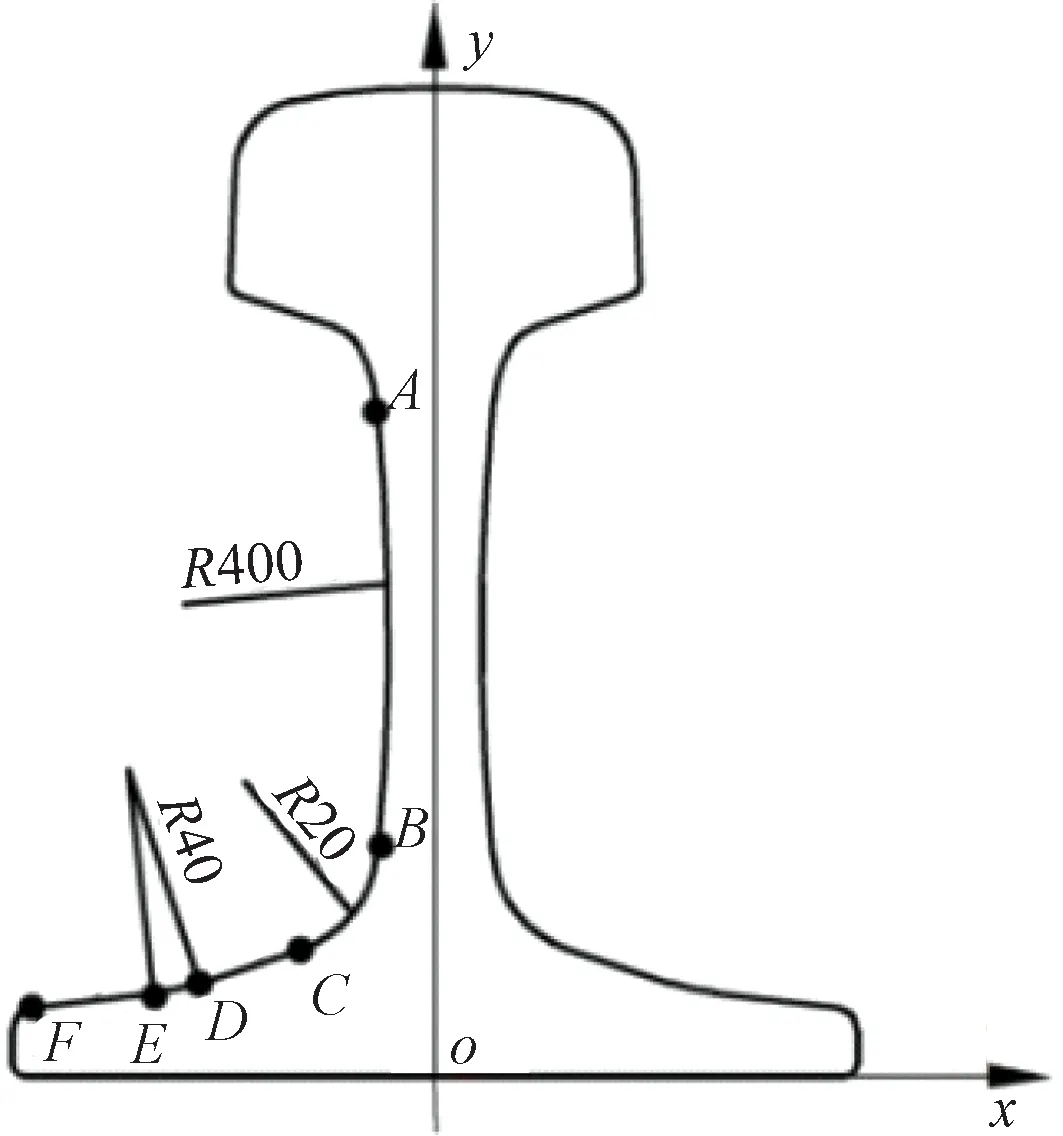
图4 60 kg/m标准钢轨断面轮廓(单位：mm)

3.1 轨腰圆弧分割方法

首先，需要从钢轨测量轮廓中分割出轨腰圆弧AB、BC，才能分别进行圆心拟合获取粗配准的基准点坐标。由于轨头的遮挡作用，使得激光无法投射在A点，测量轮廓的轨头部分与圆弧AB自然分离，因此，轨腰圆弧分割的关键是确定圆弧BC的端点。

针对测量轮廓点集，本文采用RDP算法从中提取关键数据点，利用轨廓几何特征识别圆弧端点。RDP算法是由文献[10]提出的一种基于递归思想的曲线轮廓采样算法，其基本思想是：用直线连接曲线的首末端点，设定全局固定的距离阈值，计算并比较曲线上各点到直线的距离，找出最大距离dmax，若dmax大于阈值，保留对应数据点，并作为新的端点，将原始曲线分为两段，分别重复以上过程直到所有曲线到对应直线距离小于阈值。RDP算法提取的数据点在保留原始轮廓形状特征的基础上具有平移和旋转不变性，且轮廓曲率越大，提取的特征点越密集。

设pi为RDP算法提取的特征点，标准轨腰轨底轮廓使用RDP算法提取的特征点分布见图5，其中用红色虚线标识了圆弧BC的分布区间，由图5可知，p4、p10的位置与圆弧BC的首末端点近似重合，能够作为轮廓的分割点。

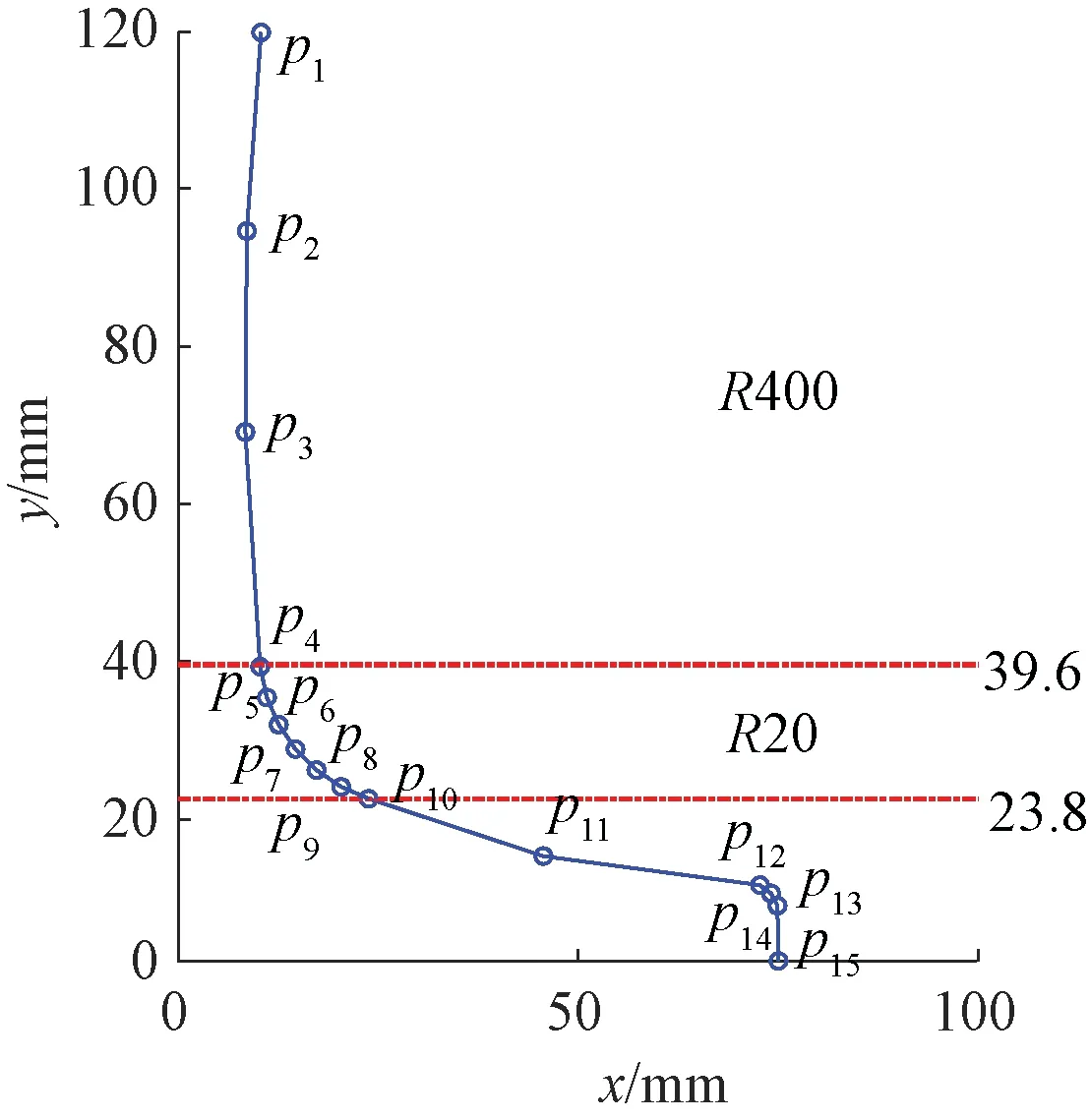
图5 标准轨腰轮廓轨底提取特征点结果

受测量噪声与距离阈值的影响，对于测量轮廓，RDP算法提取的数据点数量和位置都会有所不同，对此，结合钢轨轨腰轮廓几何形状特征，本文提出利用RDP算法提取的数据点到圆弧AB圆心的距离与半径的偏差识别圆弧BC端点。

设轨腰圆弧AB的圆心坐标为o(xo,yo)，半径R=400 mm，RDP算法提取的轨腰轮廓特征点集合为{(xi，yi)∣i=0，1，2，…，n}，则特征点(xi，yi)到圆心o的距离为

(1)

δi=|di-R|i=0，1，2，…，n

(2)

式中：δi为特征点到圆心o的距离di与实际半径R的偏差;n为拟合点数。

标准轨腰轨底轮廓提取的特征点δi分布曲线见图6(a)，其中p1、p2、p3与p4属于圆弧AB，因此到圆心o的距离等于实际半径，δi等于0，其余特征点脱离圆弧AB，并逐渐远离圆心o，因此δi不断增加，其中圆弧BC对应的特征点分布密集，故δi增幅平缓，而从圆弧BC的末端点p10开始，轮廓由较为平滑的曲线转变为直线，曲率减小，提取的特征点分布离散，相邻特征点的δi增幅明显。

将δi分布曲线局部放大后见图6(b)，由于圆弧BC的近似端点p4、p10分别对应δi增加的起点与δi增幅变大的起点，因此分别取得δi分布的局部极大值和局部极小值。本文提出设定图中红色虚线标识的双阈值Tl和Th，分别将δi小于低阈值Tl和高阈值Th的最后一个特征点作为圆弧BC的首末端点。

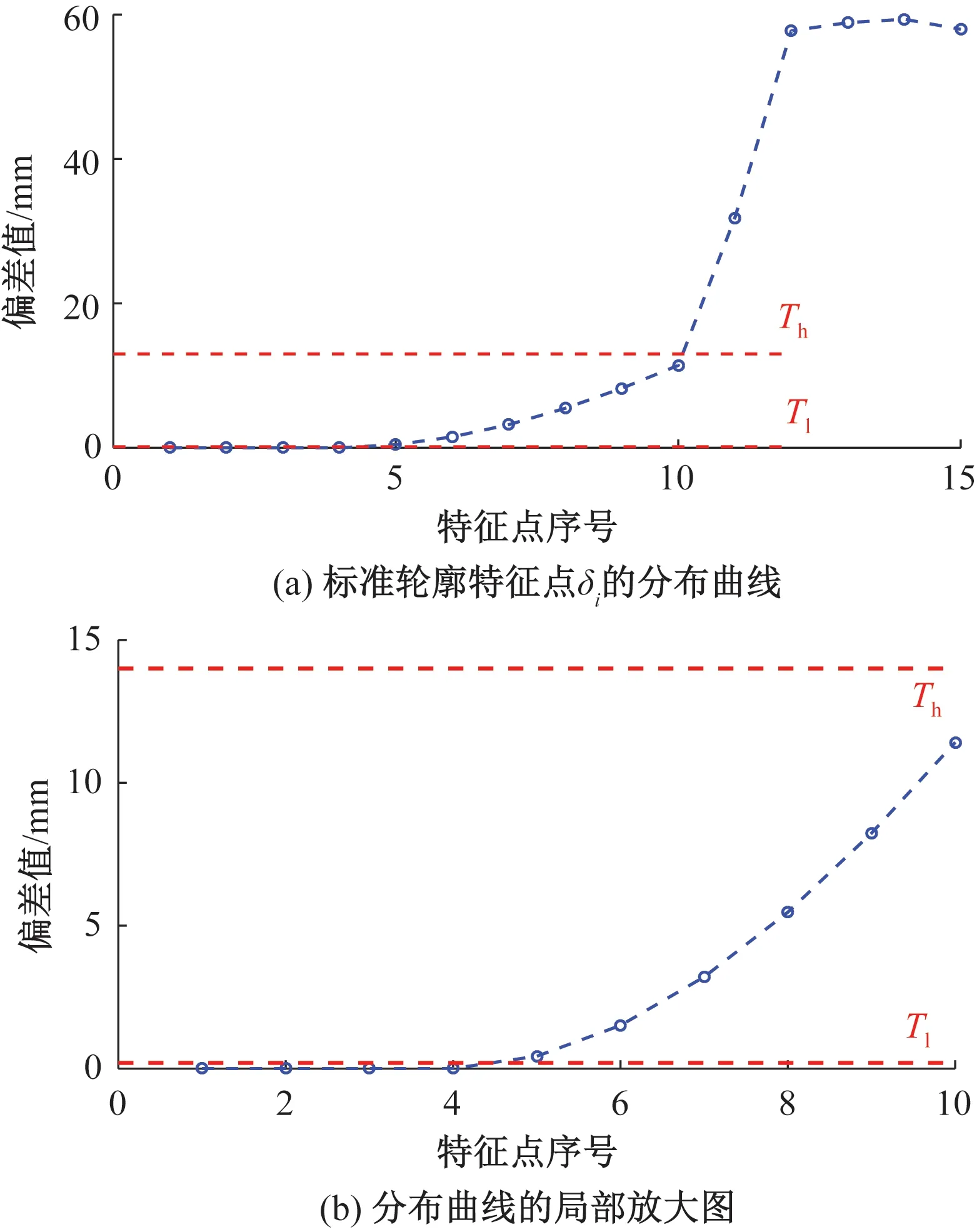
图6 标准轨腰轮廓分割点的定位

Tl和Th的选取受随机噪声与RDP算法采样点数差异影响而有所不同，实际测量时需要依据轮廓的δi分布曲线选取合适的阈值。

由于测量轮廓不在轨道标准设计坐标系下，所以圆弧AB的半径长度虽然已知，但无法直接确定其圆心坐标，鉴于圆弧AB在测量轮廓数据集中所占的比例较大，故可提取一定数量的数据集，利用最小二乘法进行圆心拟合。

但圆弧AB的长度在对应圆周所占比例较小，若直接采用最小二乘法拟合的圆心坐标精度较差。将圆弧已知半径作为约束条件添加到最小二乘法，能有效提高拟合精度[11]。设拟合圆心坐标为(xo,yo)，圆弧上数据点坐标为(xi，yi),已知半径为R，则基于半径约束的最小二乘圆弧拟合的目标函数为

(3)

式(3)是关于圆心o(xo,yo)的非线性方程，可以利用Levenberg-Marquardt[12]等非线性优化算法进行求解。

标准轮廓与测量轮廓轨腰轨底数据点曲率分布曲线见图7。与标准轮廓相比，测量轮廓受实际噪声影响，曲率特征波动明显，难以设定阈值识别出圆弧BC的端点。

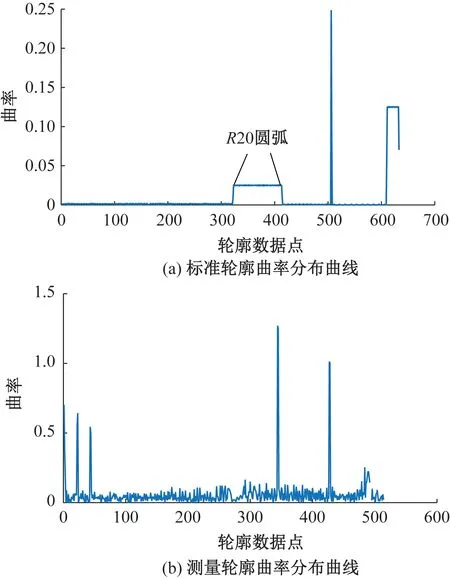
图7 钢轨轨腰轨底轮廓曲率分布

RDP算法提取的测量轮廓特征点与δi分布曲线见图8。由图8可知，根据δi分布曲线设置阈值Tl和Th后，完成了圆弧BC的分割。与基于曲率阈值的分割方法相比，基于RDP算法获取的分割特征更加稳定，鲁棒性更好，能够实现轨廓的自动分割。

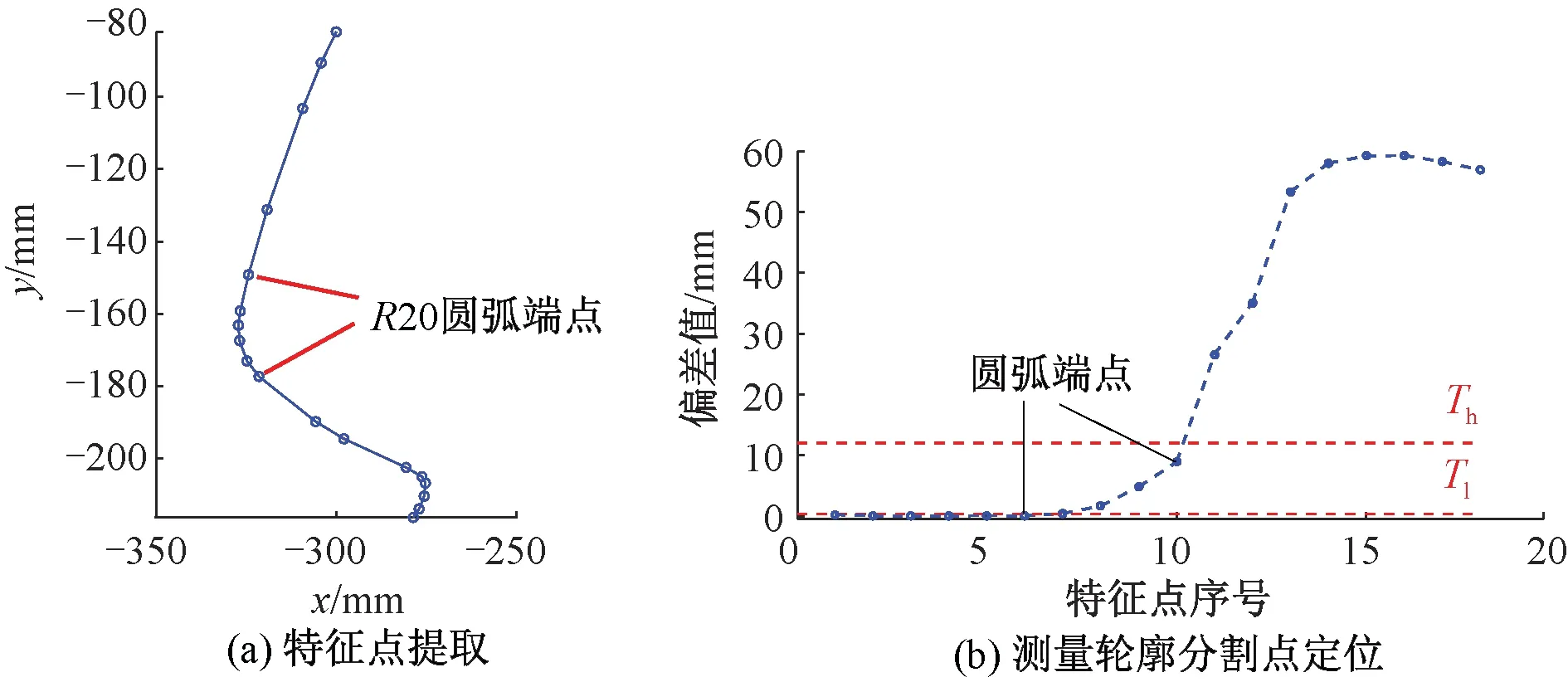
图8 测量轨腰轨底特征点提取与轮廓分割结果

3.2 钢轨轮廓的粗配准

完成钢轨轮廓轨腰圆弧分割后，需要进行圆心拟合以获取粗配准的基准点。由于测量噪声和轮廓分割误差的影响，使得拟合数据集不可避免的存在噪声，因此只进行一次拟合的圆心精度较差。为了获取更为准确的基准点坐标，本文在一次拟合的基础上，设置噪声点判别标准对拟合点集进行筛选后再拟合，可以提高圆心拟合精度。

设第一次拟合的圆心坐标为(x1，y1)，参与拟合的数据点为(xj，yj)，拟合圆弧的半径为r，则参与拟合的数据点到相应圆心的距离与半径r的偏差为

(4)

设定阈值Δmax对数据集进行筛选，将Δj>Δmax的数据点作为噪声点从拟合点集中删除后再进行圆弧拟合。为了验证该方法的有效性，选择RDP算法分割后的标准轮廓轨腰圆弧AB、BC分别进行一次和二次拟合，拟合的圆心坐标与标准圆心坐标对比见表1。

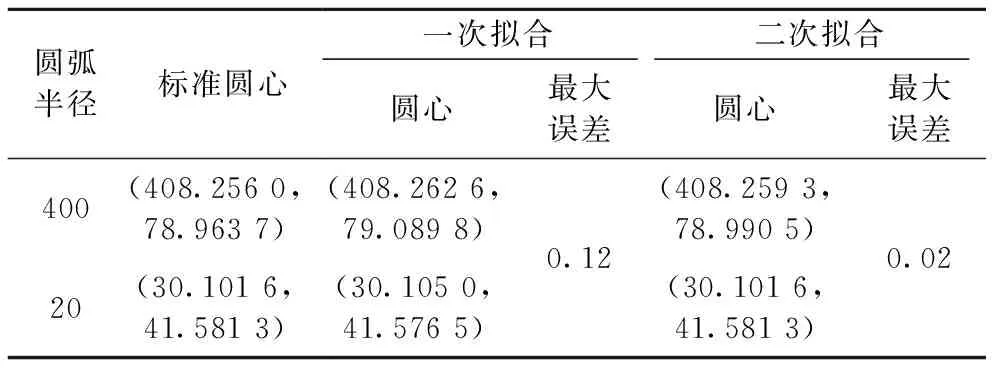
表1 圆弧圆心拟合值与标准值对比 mm

由表1可知，与一次拟合相比，二次拟合后的圆心坐标最大误差减小为0.02 mm，证明了二次拟合能有效提高圆心拟合精度。

完成测量轮廓的圆心拟合后，就可以计算测量坐标系与轨道标准平面坐标系之间的变换关系，实现测量轮廓与标准轮廓的粗配准，设测量坐标下轨腰圆弧圆心的拟合坐标为(xm，ym)，标准轨道平面坐标系下的坐标为(xs，ys)，根据空间坐标变换关系为

(5)

式中：R为旋转变换矩阵；θ为旋转角；T为平移变换矩阵；tx、ty分别为X轴、Y轴方向的平移分量。

分别将圆弧AB、BC在标准轮廓的圆心坐标和测量轮廓的拟合值代入式(5)，求解变换模型参数R、T，然后利用该模型将测量轮廓转换到轨道标准平面坐标系下，完成轨廓的粗配准。

3.3 基于改进ICP算法的钢轨轮廓精配准

最近点迭代(ICP)算法是由Besl和Mckay于1992年提出的一种数据匹配算法[13]。ICP配准算法首先搜索源点集和目标点集的最近邻点对，然后基于最小二乘准则构造点对的配准目标函数，求解旋转平移变换矩阵，并利用该变换关系，将源点集变换到目标点集所在坐标系，然后估计新点集与目标点集的误差，若大于阈值，则迭代运算上述过程，直到误差小于阈值或者迭代次数达到预期值。

ICP算法原理简单，配准精度高，但要求待配准点集之间有较好的初始位置关系，否则容易陷入局部最优解，而且迭代计算的速度受最近邻点对搜索效率的影响。3.2节的粗配准结果已经使得两个配准点集大致重合，因此主要采用KD树加快最近邻点对的搜索速度，提高配准效率。

KD树是一种用来构建高维空间数据集有序索引的数据结构，结合区域查询算法能够实现快捷高效的最近邻检索。KD树的所有非叶子节点可以视作一个超平面把高维空间在当前方差最大的维度分割成两个子空间，所有小于节点值的出现在左子树，大于节点值的出现在右子树。ICP算法利用KD树构建数据索引，能够有效提高最近邻点对的搜索效率[14]。标准轨腰轨底轮廓使用KD树构建数据索引过程见图9，其中红色、蓝色实线标记了KD树各节点在对应维度的划分值。

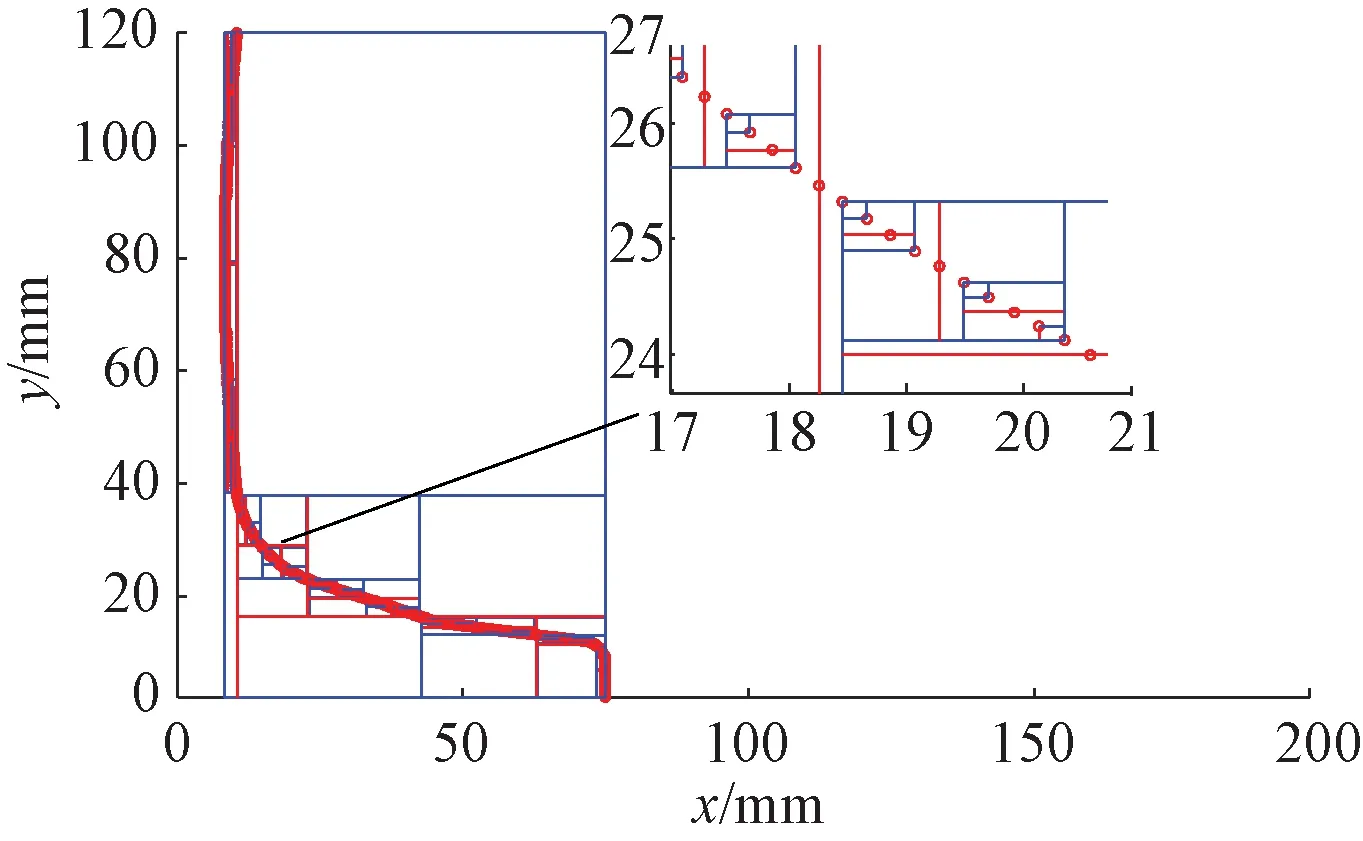
图9 标准轨腰轨底轮廓空间划分

利用改进的ICP算法完成轨廓精确配准后，就可以计算标准轮廓和测量轮廓上钢轨磨耗测量点之间的距离，获取钢轨磨耗值[15]。综上所述，本文提出的轮廓配准算法流程见图10。

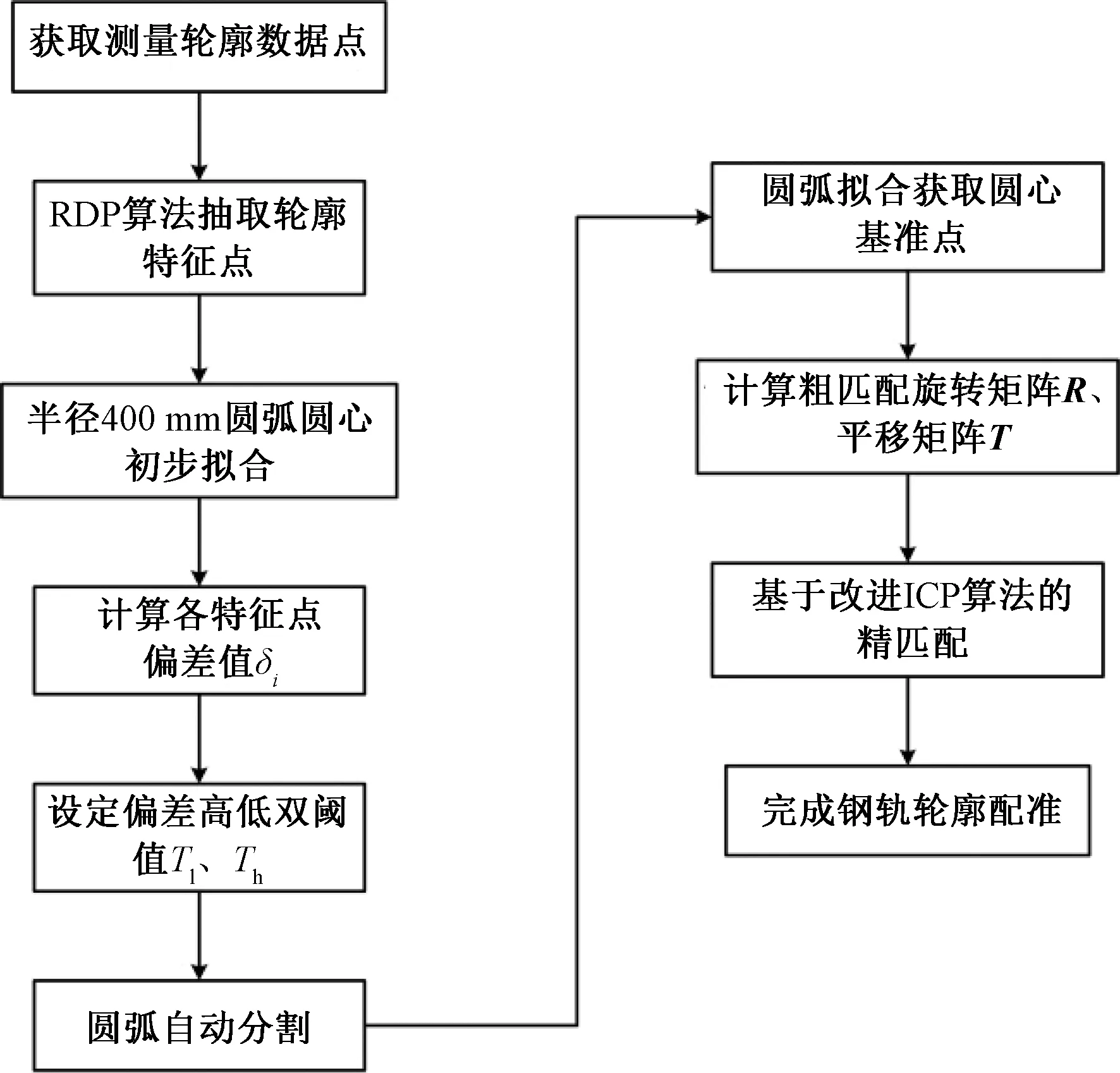
图10 钢轨轮廓自动配准算法流程

4 实验与分析

为验证轮廓配准方法的有效性以及钢轨磨耗测量系统的测量精度，在实验室环境与实际线路上分别进行了静态测试与动态测量实验。结构光视觉传感器选用Basler工业相机，分辨率为1 280×960像素，最大帧率30 fps，线激光器采用抗干扰能力强、光束均匀的650 nm红色半导体激光发射器。

磨耗测量结果与误差为0.5级的数显式钢轨磨耗尺的测量结果进行比较。

4.1 静态实验

如图11所示，实验室静态实验以60 kg/m钢轨为测量对象，分别验证二段式轮廓配准算法的有效性以及磨耗测量系统的重复性精度。

图11 静态实验钢轨结构光图像

对采集的钢轨轮廓利用本文提出的算法进行配准，前后对比见图12，配准效果良好。

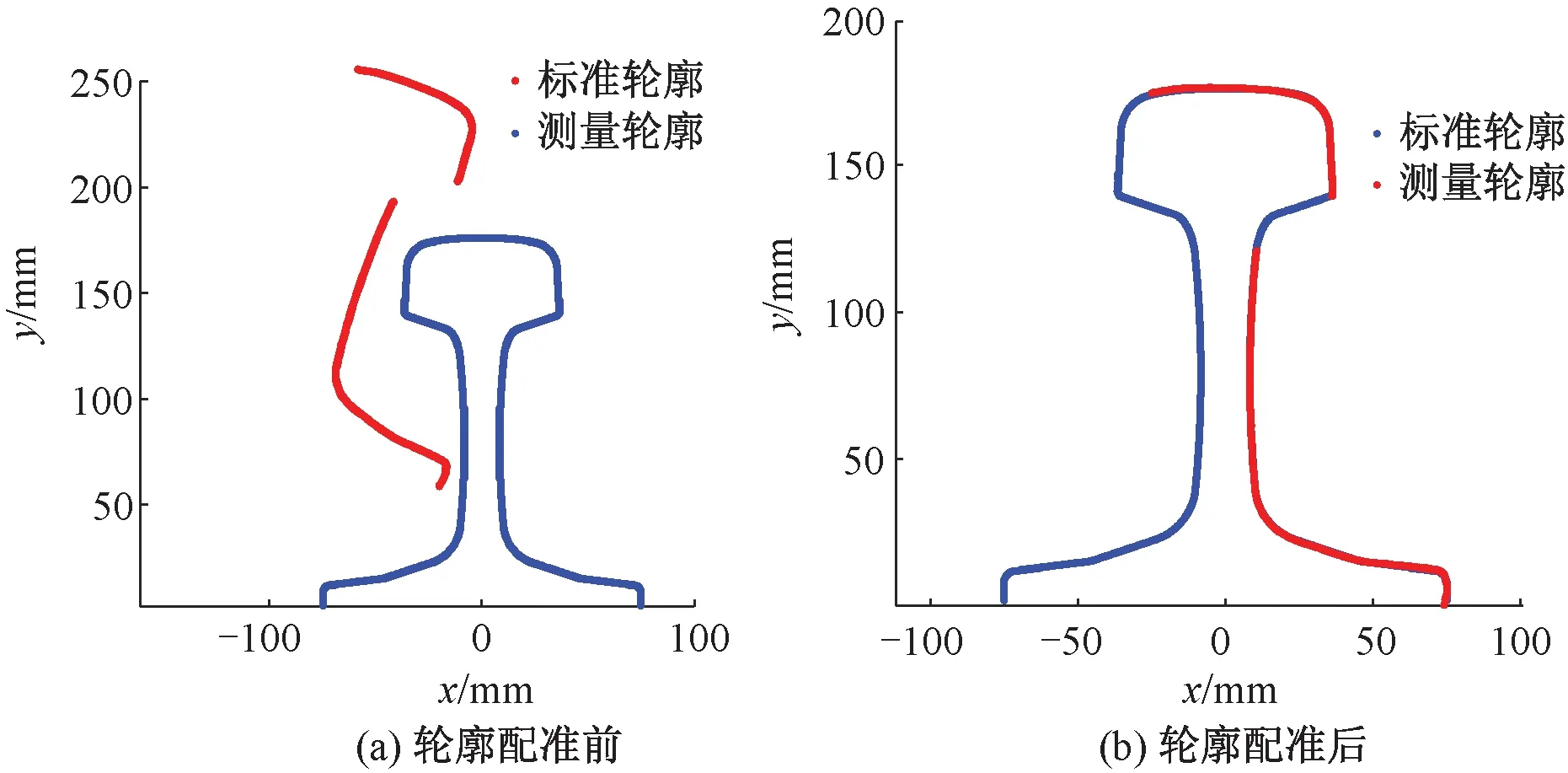
图12 轮廓配准效果

选取钢轨某一位置连续进行50次磨耗测量并统计测量系统在图像处理、轨廓配准与磨耗测量等环节所消耗的时长，如图13所示，其中系统处理单个钢轨轮廓的平均时间约为36 ms，轮廓配准的平均时间约为4 ms，效率较高。

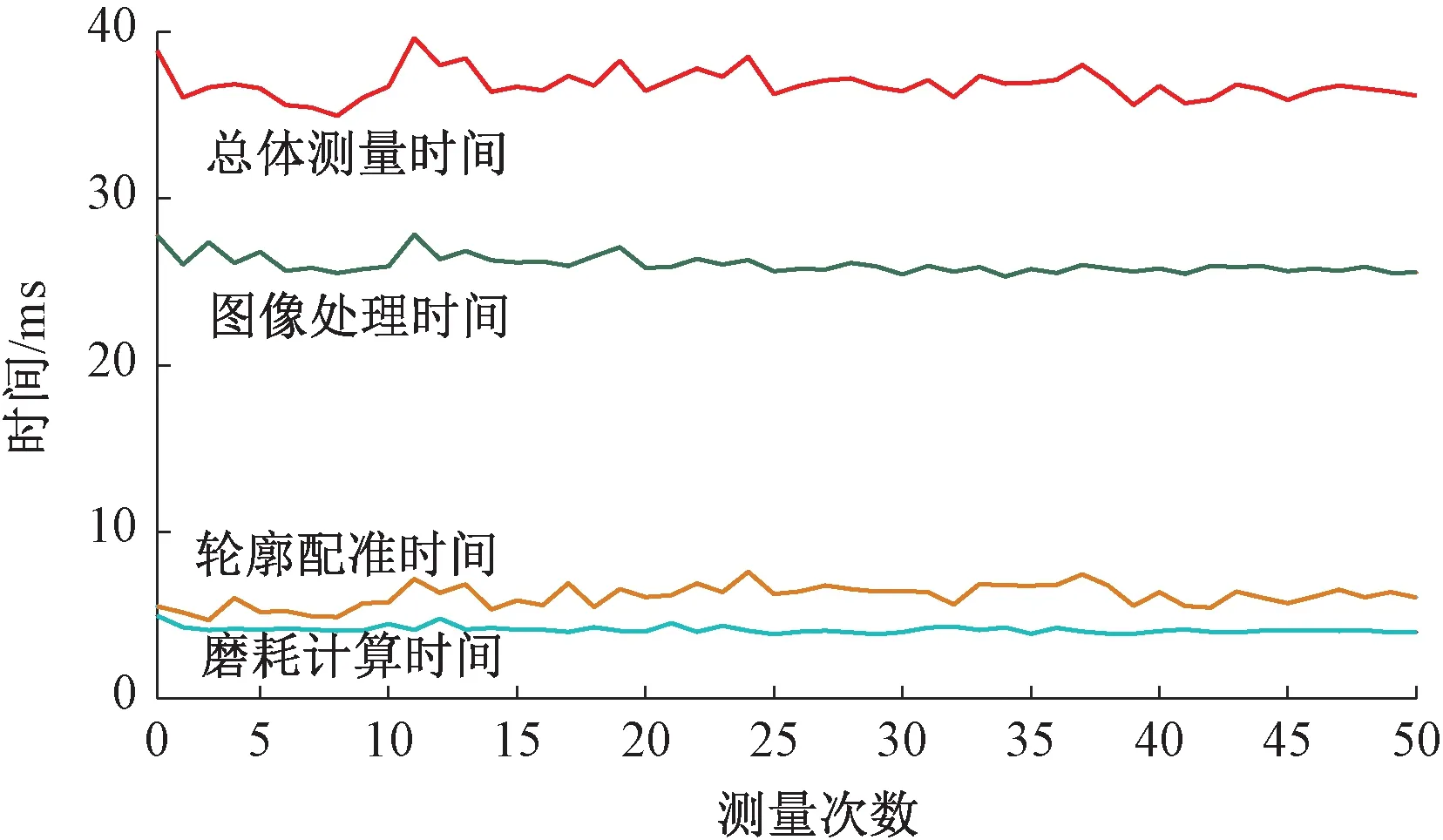
图13 钢轨磨耗测量系统处理时间

将系统磨耗测量结果与磨耗尺的测量数据进行测量精度重复性对比，结果见表2。

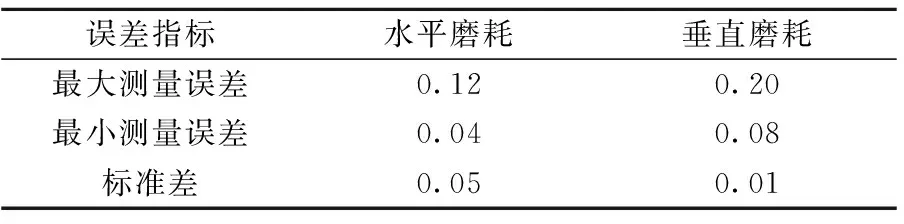
表2 静态重复性测量实验结果 mm

4.2 动态实验

在行车线路上进行了钢轨磨耗动态测量实验，推动检测小车以1～1.5 m/s速度进行测量。

每隔200 mm采样间隔，选取了40个不同位置分别进行人工测量和系统测量，磨耗测量结果见图14。

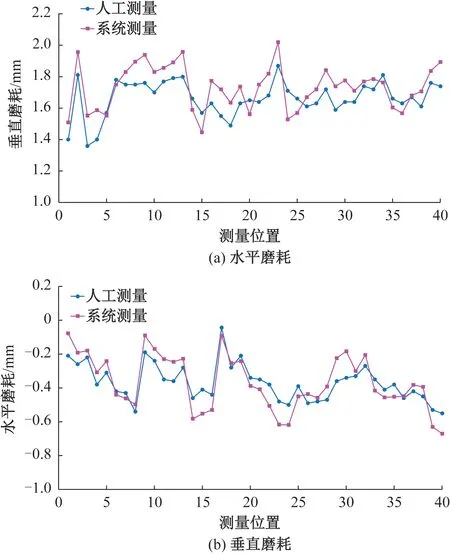
图14 动态磨耗测量实验结果

经统计，钢轨磨耗测量系统由单帧图像采集到输出磨耗值平均所需时间约为80 ms，可满足基于手推式轨道状态检测小车的磨耗实时检测要求。垂直磨耗最大测量误差为0.18 mm，平均测量误差为0.10 mm，测量误差标准差为0.048 mm；水平磨耗最大测量误差为0.16 mm，平均测量误差为0.07 mm，测量误差标准差为0.04 mm。

根据实验结果可知，利用两段式轮廓配准方法的系统动态磨耗检测精度在0.2 mm以内，满足铁路部门的测量要求，且检测效率较高，可以实现钢轨磨耗的实时测量。

5 结论

本文研究了一种搭载在手推式轨道检测小车上的钢轨磨耗测量系统，针对动态测量过程中关键的钢轨轮廓配准问题，提出了一种基于RDP和改进ICP算法的两段式钢轨轮廓配准方法。由实验室和实际线路测量实验结果可知，利用该两段式配准方法的钢轨磨耗测量系统的测量误差在0.2 mm以内，且检测效率较高，能够满足手推式轨道检测小车的现场测量要求。