基于贝叶斯网络的暴雨-地质、暴雨-洪涝灾害链推理模型

帅 敏，郭海湘，刘 晓，王德运，陈卫明

（1.中国地质大学（武汉）经济与管理学院；2.中国地质大学（武汉）工程学院，湖北武汉 430074）

1 研究背景

近年来，国内多发极端强降雨天气，引发山区、市区地质洪涝灾害，对电力、通信、公路等基础设施损毁严重，甚至直接威胁群众生命财产安全。仅2020年6月以来，南方持续强降雨已引发13 个省份的洪涝灾害，受灾人口高达1 216 万人，直接经济损失257 亿元。2020年6月23日，国家防汛抗旱总指挥部办公室针对重庆市、贵州省的强降雨情况，重点强调防范局地强降雨引发的山洪地质灾害，切实加强雨区中小河流洪水和城市内涝防范，提前发布预警避险信息；6月28日，国家主席习近平对防汛救灾作出重要指示，要求全力做好地质洪涝灾害防御。从凝练现实问题的角度出发，考虑暴雨-地质、暴雨-洪涝两类灾害链的链式反应，预测次生灾害的风险等级及基础设施的损毁程度，已成为灾害应急管理中亟待解决的关键问题。

“灾害链”的概念最早由郭增建等［1］在1987年提出，其后文传甲［2］、史培军［3］从链式特征、灾害链环等角度阐述了对灾害链的新的理解。2018年Aghakouchak 等［4］提出全球极端灾害的爆发是自然灾害级联效应所致，即多米诺式的链式反应。这其中，暴雨-地质灾害链、暴雨-洪涝灾害链作为影响范围广、破环力大的两类灾害链引发了学者的广泛关注，尤其山区地形地势条件复杂，市区设施有人为修护影响，使暴雨对次生灾害的引发形式不确定，次生灾害整体演化过程的预测预警更加复杂。因此，基于灾害链的演化机理对灾害进行模拟预测，已成为了灾害预测预警模型的研究重心。

暴雨-地质灾害链预测预警模型主要分为两类。第一类应用预测预报技术，已朝着人工智能预测预报模型、非线性预测预报模型和基于地理信息系统（geographic information system，GIS）技术的信息模型快速发展［5］，如王佳佳等［6］基于网络地理信息系统（WebGIS）和“四库”（模型库、方法库、数据仓库、知识库）一体技术开发滑坡灾害预测预报系统，通过静态的地质灾害易发性评价和动态的降雨预测耦合，划分危险性等级，进而确立预警阈值；马洁华等［7］、王治华等［8］则在选取指标及预警阈值获取方式上进行了细化。第二类利用监测预警技术实现目标区域位移、环境变化的监测，如在技术上雷达干涉测量在20 世纪90年代就被应用于监测地质灾［9］；Jaboyedoff 等［10］分析了激光雷达在滑坡、岩崩和泥石流中的不同应用，并提出从高分辨率的数字高程模型(HRDEM))中获取更多数据，用于滑坡的早期预警；Fan 等［11］研究证实采用多时间卫星或无人机图像融合监测系统测算位移的科学性。现有预报系统应用的危险性评价方法，评价指标受专家人为主观影响，且地质灾害复杂，此法考虑影响因素单一。总体来说，以上两类方法设定的最终预警阈值都未实现对灾害全过程的动态概率推理，无法基于实时动态数据实现灾害风险等级评估、从而采取相应防灾措施。

暴雨-洪涝灾害链预测预警模型主要分为两类。第一类为应用经典预测模型如人工神经网络ANNs、自回归移动平均法ARMA、灰色预测模型GM(1，1)、整合移动平均自回归模型ARIMA 等。第二类为改进水文模型，主要分析洪涝灾害的影响因素，得出有关评价指标在模型中的合理权重，如杜志强等［12］将历时降雨和实时降雨数据代入ARMA 模型识别异常降雨；刘雄［13］将易渍水点地形及单位面积降雨量作为城市洪涝的影响因素，应用回归分析得到降雨积水的关系模型。以上洪涝灾害预测模型一般针对雨涝、内涝等单类洪涝灾害节点进行预测，对于其他洪涝灾害节点间引发的关系有待拓展。

预测暴雨灾害对电力、水和通信等基础设施系统的损毁程度，必须注重它们之间的级联关系和级联效应，因为它们相互依赖，一个系统的损坏可能会在依赖于它的所有系统甚至整个系统中产生级联效应［14］。目前，基础设施间的级联关系及其在地质洪涝灾害背景下的应用已有一定的理论基础，如He 等［15］度量飓风灾害下电力、水和电信系统之间的依赖性，推测系统受损后的恢复时间对此依赖性的敏感程度；Cheng［16］提出一种非对称关系矩阵的数学框架，在涉及洪水地质灾害时可用以分析基础设施之间的依赖性，从而对其重要性做优先级排序。但如何进一步量化级联关系对基础设施的损毁程度还需要考虑。

贝叶斯网络作为对复杂系统建模和推理的工具，其构建的拓扑结构可用于解决洪涝灾害模型中未定性灾害节点间引发关系的问题，参数学习得到的条件概率表可用于定量预测地质灾害节点间的引发概率，进而通过因果推理实现对灾害过程的动态概率预测以及对基础设施的损毁等级推理，以弥补上述研究内容的缺陷。目前，贝叶斯网络已应用于灾害链、突发事件链建模、网络舆情危机等级预测等领域的研究中，如哈斯等［17］以贝叶斯网络为工具构建因果型草原干旱雪灾灾害链模型，预测干旱引发来年雪灾的影响程度；罗军华等［18］构建山区公路暴雨-洪水灾害链贝叶斯网络推理模型，研究不同情形下公路构筑物受暴雨-洪水灾害影响的破损情况。

但目前贝叶斯网络在灾害链中的应用以单灾害链为主体，仅设定发生与不发生两种节点状态，结合专家经验获取先验概率和条件概率表，本研究旨在已有研究基础上进行节点状态细分以及提升风险概率预测精度，克服无法评估风险级别的缺点和突破以往应用模型中受人为因素影响的局限，构建可普遍应用的综合灾害链模型，并以常见的地质、洪涝灾害的山区、市区为背景，探究暴雨过程中不同孕灾环境下引发各次生地质、洪涝灾害的概率，以及预测由此造成的公共基础设施损毁的程度，为有关管理部门提供有效的风险评估与决策支持。

2 研究方法

2.1 贝叶斯网络、因果推理及检验

构建灾害链贝叶斯网络模型需先建立贝叶斯网络图，据此运用因果推理实现概率预测，最后在实例检验中通过计算实际值与预测值的均方概率误差，即Brier 评分来检验模型精度。

因果推理是利用贝叶斯网络的正向因果推理技术，在已知一定的父节点状态（证据）的情况下计算子节点发生的条件概率，即进行预测［24］，基于已构建的贝叶斯网络图，在已知原生灾害父节点的状态下计算次生灾害子节点不同状态下的条件概率，得出最终风险等级。如在灾害链式反应过程中，所有影响灾害节点发生的父节点Si组成的集合为证据Sa，这种情况下次生灾害子节点Sb处于状态的概率为，计算如式（1）所示。

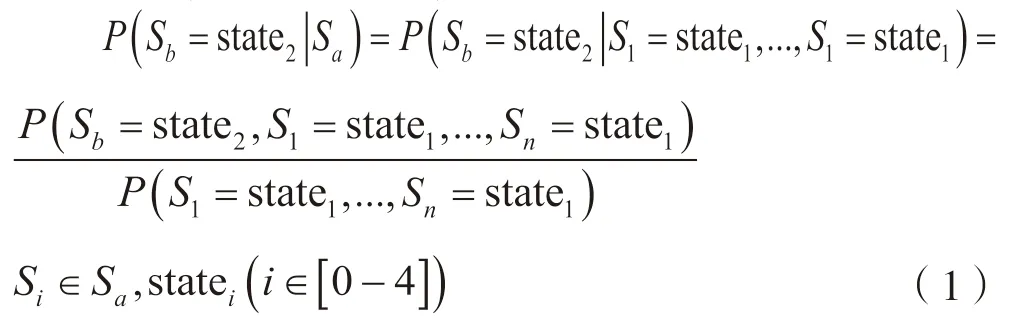
式（1）中：n为灾害节点个数，每个灾害节点都有i种状态；表示给定所有原生灾害父节点的状态为时，次生灾害子节点Sb处于状态的概率；表示所有灾害父节点状态为和次生灾害子节点Sb状态为同时发生的概率；表示已发生的事件即所有父节点状态为的联合概率。

本研究采用贝叶斯网络模型评价常用标准Brier评分对模型预测效果进行评价。Brier 评分假设贝叶斯网络模型中第i个评价目标为，m为待评价变量个数，每个Mi有种可能的状态，变量Mi的第j种状态取值Mij所对应的推理概率为；变量Mi的实际取值记为，若Mij恰好为该变量的实际取值，则；否则。记：，其中B代表贝叶斯网络中m个目标变量的预测偏差平均值，，B越小则代表网络预测偏差越小，即预测效果越好。一般认定：则表示该网络预测结果的正确性符合要求；反之，不符合要求。

2.2 贝叶斯网络建模

2.2.1 贝叶斯网络节点选取

首先，将暴雨在山区、市区不同情景下易发生的地质、洪涝灾害链进行节点划分；其次，根据国家减灾网、各地方政府网站、新华网、新浪网、搜狐网、百度百科等权威网站的灾害报道数据，并结合专家意见，选取常见的24 个节点变量，如表1 所示 。

表1 山区、市区暴雨灾害链节点变量

2.2.2 贝叶斯网络结构建立

本研究以美国Web of Sciences、中国知网数据库为文献收集库，搜索降雨、滑坡、泥石流、山洪等灾害节点关键词，得到相关的灾害文献，分析灾害节点影响因素，据此构建出贝叶斯网络结构中各节点的引发关系，得出山区暴雨-地质灾害链、市区暴雨-洪涝灾害链的贝叶斯网络拓扑结构，如图1 所示。其中，地质类灾害文献主要研究对象为滑坡、泥石流、堰塞湖，此类灾害形成的必要条件为松散物质来源，如地质结构不稳定、岩性风化、人为活动等，本研究选取地质和岩性结构两个最为普遍的因素。泥石流以土壤松散、携带大量泥沙为主，易在陡峭地形上迅速形成、流通、堆积，最重要的诱发因素为水源条件，可以带来搬运物质的动力且软化土壤；堰塞湖是由上游的泥石流堆积的松散物质冲入原有水系，导致河床堵塞，储水而形成。洪涝类灾害文献内容主要涵盖农业的雨涝灾害风险评估、市区内涝灾害应急管理、洪水灾害预测预警。雨涝主要危害农作物，造成减产绝收；内涝常见于地势低洼、排水系统老化的老城区；洪水危害程度则远超其他洪涝灾害，直接引发河流湖泊的水位上涨，冲毁房屋基础设施，造成人员伤亡。承灾体选择易受山区、市区地质洪涝灾害损害的主体，即公共交通、电力系统、通信系统、人员伤亡、房屋倒塌等节点。电力系统由于依靠电线杆输电，洪水冲断电线杆就易引发多个地区如乡、县的大面积停电；通信光缆被山洪、泥石流灾害冲断，基电站存电量耗完则通信因此中断；滑坡、泥石流在山区发生后，由于山区房屋分布零落、人口密度小，故房屋倒塌数量少、人员伤亡基数小，但人员伤亡情况重；市区易发生洪涝，虽受灾人口广布，但是灾害应急措施成熟，人员伤亡少，然房屋倒塌受损数量多；洪水导致水厂被淹、供水管道被毁，则严重影响了城区市民用水。

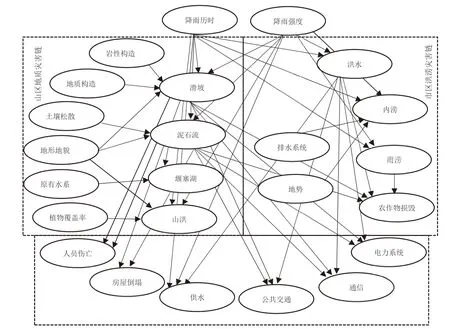
图1 山区、市区暴雨灾害链贝叶斯网络结构

2.2.3 贝叶斯网络各节点的状态取值及条件概率表分布

哈斯等［20］、罗军华等［23］在进行贝叶斯网络节点状态划分的时候，为降低网络节点参数估计的复杂性，多采用二值化离散处理，结合专家经验，划分为灾害事件发生和不发生两种状态。本研究为了使预测结果更加精确，明确事件发生时的严重程度，参考了我国国家气象局、地质灾害防治工程行业标准及相关文献，在部分节点上划分了多种状态，具体如表2 所示。

表2 暴雨灾害链贝叶斯节点的状态取值及先验概率

表2 （续）

从国家减灾网、政府门户网站、新华网等官方网站获得灾害事件数据，再应用期望最大化(expectation maximization，EM)算法进行参数学习，得出表明父节点、子节点间概率关系的条件概率表。以山区发生的暴雨灾害子节点堰塞湖为例，山区发生泥石流，且附近有原有水系，则发生堰塞湖的概率较大，但是如果不存在原有水系，即使发生泥石流，触发堰塞湖的概率也很低（见表3），这说明原有水系是除泥石流以外影响堰塞湖成灾的一大因素。

表3 堰塞湖节点的条件概率

以市区发生的暴雨灾害子节点农作物受灾为例，随着雨涝从无到有到演化程度的加深，农作物受灾面积的预测结果从0.857 大概率农作物无损毁到90%以上的概率有0.01 km2～500 km2的农作物受灾，到最后雨涝程度为重度雨涝时甚至有小概率导致500 km2～1 000 km2甚至以上的农作物受灾（见表4），这说明雨涝是直接影响农作物受灾面积的最重要因素。

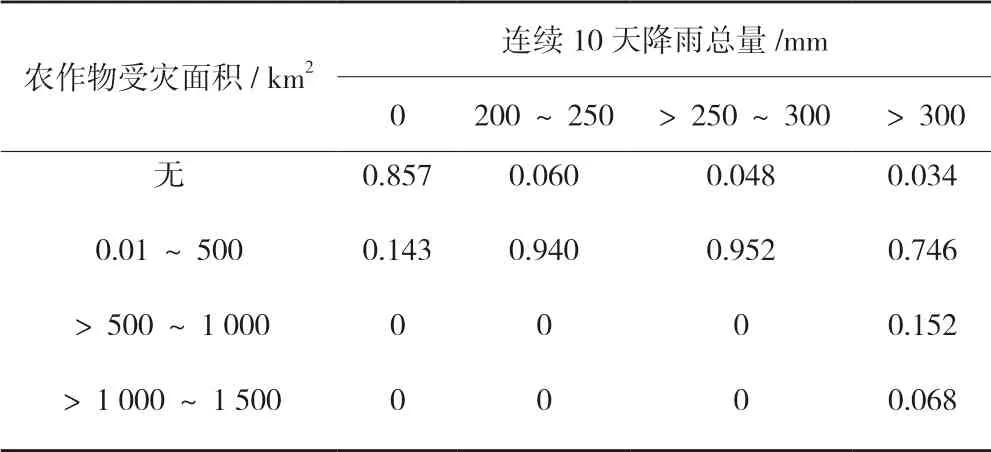
表4 农作物受灾节点的条件概率

2.3 基于因果推理的内涝严重程度预测

利用上述构建的贝叶斯网络模型进行推理，如果在灾害链链式反应过程中已经观测到a10降雨量为即200 mm 以上，a11降雨历时为即48 h 以上，b22 地势为即低平，b21排水系统为即差，则在模型中输入证据和等，经过因果推理，得到此时内涝不发生的概率为16.66%，处于一般规模的概率为16.66%，严重的概率为66.68%（详见表5）。

表5 内涝节点的条件概率

3 贝叶斯网络模型的实例推理分析及Brier 检验

3.1 实例概况

宁乡县位于湖南省长沙市，其地形地貌复杂，西部山区属于风化花岗岩地区，遇到强降雨很容易发生山体滑坡、泥石流等山洪地质灾害，东部地区属于洞庭湖尾闾地区，地势低洼，河流汇集。2017年6月22日至7月1日宁乡县发生了强降雨，导致中西部9 个乡镇出现山体滑坡，东部区域出现洪水漫堤，受灾人口达81.5 万人，占全县人口的56%，因灾死亡44 人，农作物受灾212 km2，损毁倒塌房屋14 000余间，毁损堤坝900多处，70多条道路受损，13 个乡镇停电，7 个乡镇通信一度中断，造成直接和间接经济损失约90 亿元。

3.2 实例分析及Brier 检验

利用本研究建立的贝叶斯推理模型对2017年宁远县遭受的洪涝及其地质灾害进行推理预测，设定灾害发生时已存在的证据变量概率为1，利用因果推理求出此时目标变量所有状态的概率取值，并选取其所有状态中推理概率最大的值作为预测值。将降雨强度200 mm/d、降雨历时超48 h、山区土壤松散、地形地貌陡峭、市区地势低等作为已知证据变量输入贝叶斯推理模型，根据本研究构建的灾害链式反应拓扑结构及条件概率表，应用因果推理实现对滑坡、泥石流、堰塞湖、洪水、雨涝、内涝、电力、供水等地质、洪涝、基础设施灾害节点的不同状态概率预测，选取概率最大的状态值对应识别节点的风险等级，Brier 评分B 值为0.3，小于0.6。从实际应用效果来看，区别于其他模型只有发生与不发生的状态，本研究建立的模型状态细分，直接识别相应风险等级范围，且预测值与2017年宁远县灾害链的实际数据作对比后发现较为相符（见表6），表明基于贝叶斯网络构建的暴雨-洪涝、暴雨-地质灾害链推理模型预测的准确性较好。

表6 案例暴雨灾害风险预测值与实际值对比

4 结论

现有的地质、洪涝灾害链预测预警模型集中在具体区域的单灾害链风险预警，导致模型的普遍应用性不强，且缺乏对其他灾害类型级联效应关系的挖掘及链式反应全过程中风险等级的概率推理，而贝叶斯网络作为建模和推理的工具，运用其构建的拓扑结构可用于定性分析灾害节点间的引发关系，通过参数学习得到的条件概率表可用于定量预测灾害节点的引发概率，且在灾害链领域已有所应用，故本研究采用贝叶斯网络构建暴雨-地质、暴雨-洪涝灾害链推理模型，对灾害链中所有涉及的节点进行状态细分，构建灾害链拓扑结构，应用EM 算法获取各节点的条件概率表，以此进行因果推理，预测暴雨造成次生灾害的风险等级及其对基础设施的损坏程度，并以湖南省宁远县2017年6月22日至7月1日间发生的地质洪涝灾害为例，预测结果经Brier 检验后B 值小于0.6，证明本研究构建的模型效果良好。

相较于以往在单灾害链的应用，本研究构建的模型更具有普遍综合灾害链的应用功能，且在理论上，对丰富链式反应推理及改进精度上可能存在如下贡献：（1）选取暴雨引发的次生地质、洪涝灾害节点及损毁的基础设施节点，并在节点状态分布上由单一离散型变为多范围细分型，改善以往应用模型只能预判灾害发生与否的情况，实现风险等级判别，为应急管理预案的匹配提供决策支持；（2）应用EM 算法实现了从依赖专家群决策修正条件概率表到对样本进行参数学习获取条件概率表的跨越，避免了主观因素的影响，提升了次生灾害概率预测的精度。在实践上，本研究构建的模型服务于国家重点战略，响应国家关于加强洪涝、地质灾害预警的指示，对暴雨引发的次生灾害以及由此损毁的基础设施的风险等级进行概率预测，为相关部门及时开展识别滑坡、泥石流等地质灾害隐患点、根据洪水风险等级及时安排人员转移安置、结合基础设施级联效应所预测的损毁程度进行抢修等工作提供科学依据。

本研究设定的贝叶斯网络结构对基础设施节点之间的相关关系未进行深入分析，未来的研究可深入探讨当某项基础设施受暴雨灾害影响出现故障时，引发其他基础设施出现级联故障的概率，进一步为及时防灾减灾提供决策参考。