基于巷道风流分布规律的风量计算

李亚俊，李印洪，姚银佩，钟生元，吴洁葵，邓望跃

(1.湖南有色冶金劳动保护研究院，长沙 410014；2.非煤矿山通风防尘湖南省重点实验室，长沙 410014)

矿井通风系统测定巷道中风流速度时多采用的方法为走线法及点测法，走线法主要使用翼式风表在测风巷道沿既定路线测定单位时间内巷道断面的平均风速[1]；点测法则使用热敏式风表对巷道内多个特定位置风速进行测定，并以多个测点风速的平均值作为实际风速测量值，而巷道风流运动时各位置风速不完全一样，部分线路及特定点不能代表实际平均风速[2-3]。因此，走线法和点测法在实际测量时均会出现较大误差[4-5]。

为减少实际测量误差，此次研究拟对实际巷道断面风流分布进行研究，运用数学模型表示其分布规律，并在此基础上实现对巷道实际风量进行更精确的计算。

1 风速试验测试

1.1 测定系统

试验系统采用如图1所示的结构，装置截面为圆形[6-7]，装置动力由具有变频控制风速装置的风机提供，测试系统的风流在变频风机作用下，经装置右侧的整流格栅进入系统。为方便试验测试，装置中部设有高速和低速测风口，以便试验测定巷道断面各处风速值。

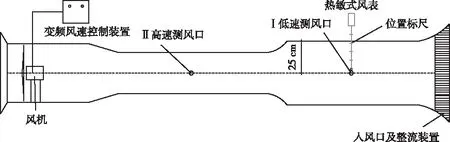
图1 测试系统结构Fig.1 The structure of test system

1.2 试验流程

测试利用装置低速测风口，测定该处断面各位置风速，并利用装置的位置标尺记录各测点与巷道中心轴线距离，从而记录巷道各不同位置处的实际风速值，风速测量装置选用宜于操作的热敏式风表。同时，为测试不同风速下巷道不同位置处的风速变化，试验测试时通过变频器设置风机档位为低、中、高三档，重复测试步骤测定低、中、高档位各点风速测定。

2 研究测试

2.1 测试分析

以测试断面中轴线为参考位置，测定距离测试断面中轴线不同位置处的风速值并记录，测试圆形断面直径为0.5 m，沿中轴线对称测定各点风速值，测点间隔小于5 cm。不同风速条件下(高速、中速、低速)重复试验测试，测试数据整理结果见表1，根据整理数据以风速值为纵坐标，距测定断面中轴线距离为横坐标，绘制表1对应的风速变化曲线图见图2。

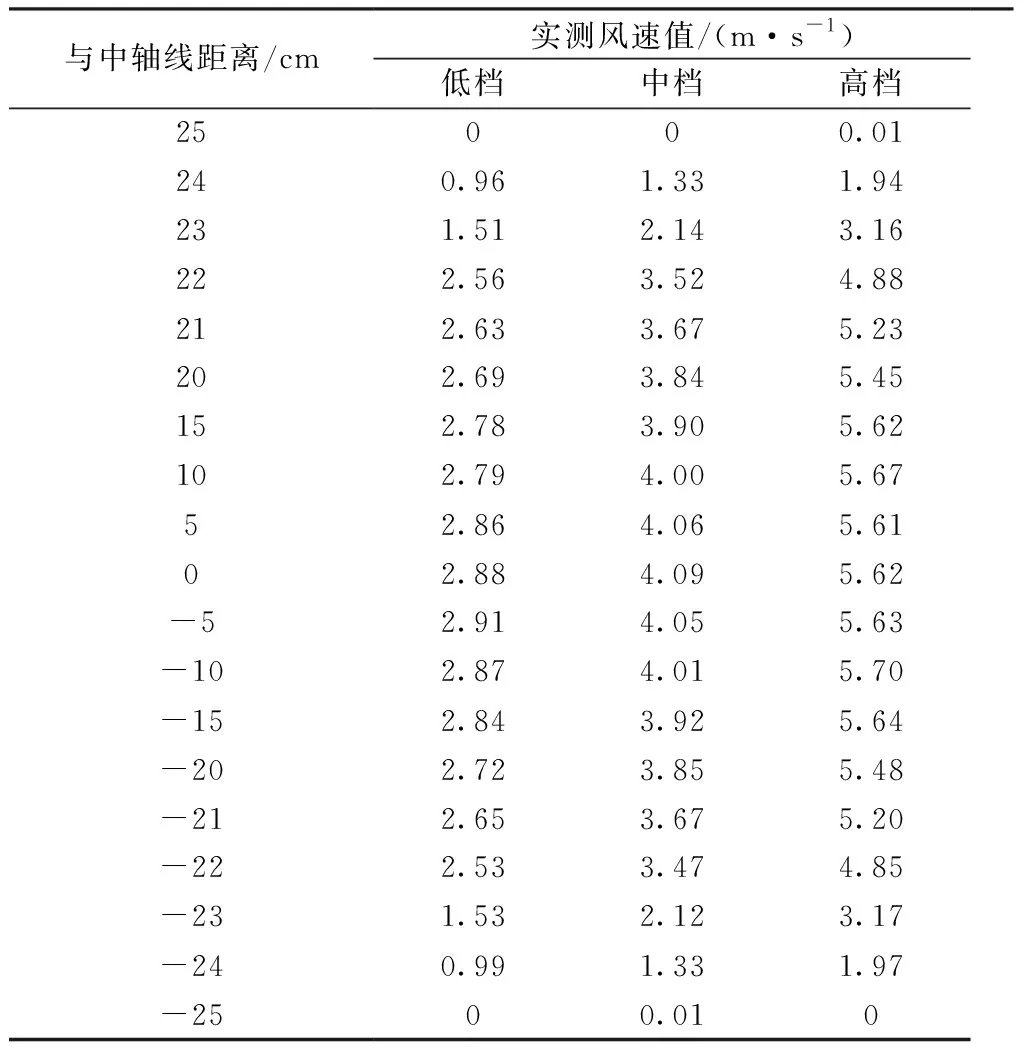
表1 测试数据整理

图2 风速变化曲线Fig.2 Wind speed curves

2.2 测试结果分析

从上述试验结果并结合图2风速变化曲线，可知各风速条件下风速分布规律基本一致，即风流分布呈现距离巷道中轴线越近，风速越高的整体趋势[8]。结合图2所示这种分布规律区别于简单的线性关系，更类似于指数形式的数学关系，分析其原因是由于巷道壁并非绝对光滑，存在一定粗糙度[9-10]，靠近边壁的风流受巷道壁的黏滞，这种黏滞作用越靠近边壁越明显，实际测定时应考虑巷道壁对风速的黏滞作用，其作用范围与巷道实际的粗糙度有关[11]。

2.3 风流变化规律数学模型表示

根据2.1及2.2节的试验结果及分析，指出巷道风流分布规律大体趋势为类指数形式。因此，为将风流分布规律利用数学模型表征，研究拟以实际测定风速值为目标函数值V(x)，对应各实测点的位置(距巷道壁距离)为自变量x，利用以自然常数e为底的指数函数形式，对其进行非线性回归分析，得出相对应的回归方程，以建立巷道断面风流变化的数学模型。鉴于实际风流变化是以巷道中轴线对称分布，为简化回归数学模型，研究仅以巷道轴线对称的一侧测定数据(自变量取值范围0～25 cm)做回归分析。采用以e为底的指数函数形式，对不同风速(高、中、低)下巷道风流变化回归分析，其回归方程表示具体如下：

1)低风速回归方程

V(x)=-2.99e(-x/1.96)+2.89

(1)

2)中风速回归方程

V(x)=-4.23e(-x/2.01)+4.09

(2)

3)高风速回归方程

V(x)=-5.89e(-x/1.96)+5.73

(3)

绘制各回归方程曲线如图3所示。

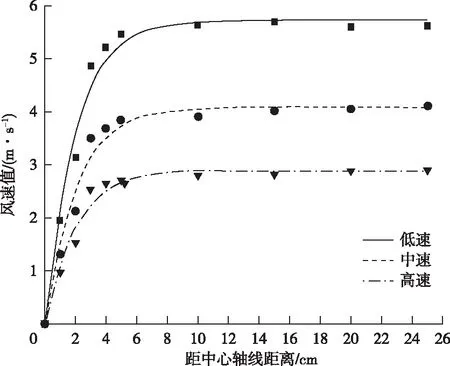
图3 三种风速条件下回归方程曲线Fig.3 Regression equation curves under three wind speed conditions

各回归方程的相关度与均方根误差值如表2所示。

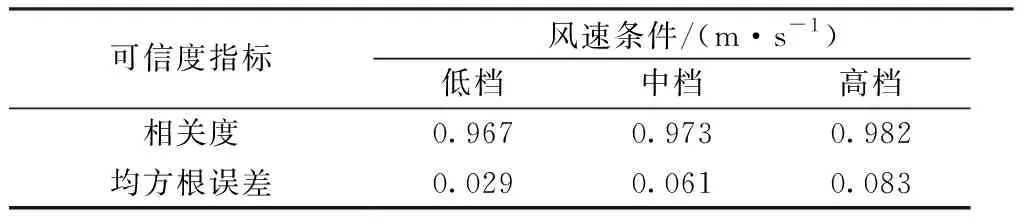
表2 回归方程可信度分析

回归相关度和均方根误差作为回归可信度分析的重要指标，从表2各指标数据分析，该回归方程可信度较高，可以作为风流变化规律的数学表示模型。

2.4 巷道风量计算

根据式(1)～(3)，将所测同一巷道断面不同位置风速的离散点，用数学模型拟合出风速与巷道壁距离间关系连续变化的曲线。由于研究的模拟巷道为圆形巷道，具有统一对称性，即上述研究所揭示的风流分布规律在圆形巷道各个方向上均一致。因此，在距离巷道壁同样距离处风速相同，整个巷道的风速分布变化应是形成距巷道壁距离相关的等速圈的形式，如图4所示。根据上述研究数学关系方程做轴线，某点风速V与其在轴向增量△x所示圆环面积的乘积即为该环内的风量，由此对整个圆形区域风量做积分，得出圆形巷道实际精确风量。根据图4有如下巷道断面内风速与风量间数学关系：

(4)

式中：Q为巷道风量值；V(x)为风速与距巷道壁距离x的关系函数。

将(1)～(3)代入(4)式得出如下关系式：

低速条件计算风量：

(5)

中速条件计算风量：

(6)

高速条件计算风量：

(7)

图4 巷道风流分布变化示意图Fig.4 Sketch map of airflow distribution change in roadway

分别对低、中、高速条件下所示积分方程进行计算，并将计算结果单位转换为国际单位，得到结果见表3。

表3 巷道风量计算结果

2.5 巷道风量计算值与常规测定值对比

若常规巷道测定风量采用分格定点法，忽略靠近巷道壁的低风速区域，依排除低速区其他风速平均值作为巷道的平均风速，则此时低、中、高速档位对应的测定风量及其与巷道实际风量计算值间的数值对比如表4所示。

由表4可知，实际巷道通风测定若不考虑巷道边界区域风速低速区，则实际测定风量将高于计算风量值，约高出15%。巷道边界低速区的存在是由于风流受到巷道壁的黏滞作用，这种黏滞作用与巷道的粗糙度有关系，实际风速测时应考虑此黏滞作用对风速、风量的影响。有关巷道粗糙度造成巷道风流黏滞与巷道边界低速区域大小的关系需做进一步研究。

表4 巷道风量测定值与计算值对比

3 结语

通过对模拟巷道风流分布规律进行研究，以巷道风流分布规律为基础采用曲线回归拟合分析与积分计算相结合的方式，对巷道实际风量精确计算，此次试验研究结果总结分列如下：

1)三种风速条件下(高、中、低档)，巷道风流分布变化趋势大体一致，风流在巷道中的变化趋势与风速无关。

2)以风速为目标值V(x)，以距巷道壁距离为变量X，对三种风速条件下试验数据进行曲线拟合分析，得出相应的回归方程。根据回归方程可信度分析，回归方程可靠性极高，可作为该类型巷道风流变化规律数学表征模型，并可作为巷道风速值连续变化计算依据。

3)利用回归方程V(x)与距巷道壁x间的连续关系，构造相应的积分方程计算出巷道的实际风量值，结果显示风量计算值与实际测定值之间存在约15%的误差，实际通风测定时应考虑该误差。

4)由于巷道壁粗糙度而形成对风流的黏滞作用，使风流在靠近边壁处，风流速度较小，越靠近巷道中心区域，风流受此黏滞作用越不明显，风速也越大。有关巷道粗糙度造成巷道风流黏滞与巷道边界低速区域大小的关系需要做进一步研究。