MATLAB软件融入高等数学课程的模块化设计与研究
2021-04-02张茜
张 茜
(西安铁路职业技术学院,陕西 西安 710600)
通过对我院高等数学课程的教学现状进行深入的调查与分析,研究将数学软件与高等数学课程进行有效融合的方案,从而提高高等数学课程的教学效果。
一、高职数学教学的现状
为了了解学生目前在学习高等数学中面临的困难,对我院学生开展高等数学课程问卷调查。采用网络调查的方式进行,问卷回收的有效率为95%。对收集到的数据进行分析汇总,得到高等数学教学现状如下:
(一)学生学习的基本情况
1.学生兴趣较高,但基础薄弱、学习主动性较差
学生刚进入大学,对学校的很多活动和课程都有着较高的热情。但是,由于高等数学高度的抽象性、严密的逻辑性、超强的衔接性,以及学生基础知识薄弱,对理论知识缺乏理解,影响了后续课程的学习,学生在学习中的快乐情绪逐渐消失,使很多学生失去了学习的兴趣。同时,学生对于高数课程的学习积极性和主动性较差,对没有学懂的知识,不采取主动措施将其搞懂弄会,长此以往,不会的知识越来越多,逐渐对高数课程的学习失去了信心。
2.学生学习方法的欠缺
很多学生没有好的学习习惯与方法。课前没有进行有效的预习,没有目的的听课,抓不住讲授内容的重难点,学习效果大打折扣。课后,大部分学生仅限于完成老师布置的作业,缺乏对所学内容的系统复习和练习,难以对相关知识点进行理解和把握。
(二)课堂的教学状况
教学方法与段单一,缺乏创新,是目前课堂教学存在的主要问题。高数课时少,学习内容多,教师每节课给学生讲授的知识都想尽可能地全面,教学手段仍然是粉笔加黑板为主,学生的学习也只是被动地接受。在调查中发现,有一半以上的学生表示所在班级的高数课堂氛围平淡、沉闷,以老师讲为主,学生偶尔参与。在问到高数课为什么课堂气氛沉闷时,学生投票较多的因素是:高数本身枯燥无味,内容脱离实际,学生独立思考的时间少,教师教学手段单一。这与学生所喜欢的“由教师设置问题,师生讨论解决问题”“以学生为主体”的教学方法相抵触,不利于学生的学习[1]。
(三)教学内容的学习情况
通过调查发现,在各个重点版块中,均有27%—40%的同学在学习上会遇到困难。各知识点内容可分为原理知识、计算问题和知识应用三大类型。其中觉得困难最多的是对原理知识的理解,最主要的原因是其抽象性强、不够直观、推导过程复杂枯燥。其次是计算问题,主要原因是计算过程复杂、计算类型多样。认为实际问题是难点的多半是因为学生平时接触到的实际问题较少,不会将实际问题数学化。
二、MATLAB软件融入高等数学课程的意义
MATLAB软件学生使用方便,手机版App的出现,学生可以随时随地应用该软件。学生的抽象思维能力较弱,他们更希望能够将抽象的知识可视化。MATLAB软件具有强大的绘图功能,可以使抽象的理论知识变得直观,使学生能够高效的内化知识[2]。有部分学生初高中数学学习不牢固,在计算时频频遇到困难,打击了他们的自信心。MATLAB软件具有强大的计算功能,可以方便地求函数的极限、导数、积分等问题,提高学生的计算效率。结合MATLAB软件强大的数据处理功能,可通过数学模型来解决实际问题,培养学生的实际应用能力。
三、MATLAB软件融入高等数学课程的模块化设计
针对学生学习中面临的困难,将高等数学中的重难知识点分成三个模块:原理探究模块、数值计算模块和数学建模模块。
(一)原理探究模块
1.重难点内容
函数与极限:基本初等函数及其图形,复合函数的概念,数列和函数极限的概念,无穷小及其性质,无穷小的比较,极限的四则运算法则,两个重要极限公式。
导数与微分:导数的概念和几何意义,函数和、差、积、商的求导法则,基本初等函数导数公式的推导,复合函数的求导法则,微分的概念。
不定积分与定积分:不定积分的定义和基本公式,换元积分法,分部积分公式,定积分的概念与几何意义,定积分的性质,牛顿-莱布尼茨公式,定积分的换元公式与分部积分公式。
2.设计原理
利用matlab强大的绘图功能,变抽象为直观。
3.程序要求
教师提供基本的matlab程序方案,学生理解方案意思,能够灵活利用程序亲自动手操作探究。
4.教学方法
主要采用任务驱动法、直观教学法和小组讨论法。在任务驱动过程中,教师设计知识点的任务单和分析单,使学生在一步步完成任务的过程中理解知识。
5.设计意图
软件画图、直观感受:学生觉得图像的绘制困难,没办法形成图形的直观想象。通过matlab绘图功能,画出相应的函数图像,学生对该知识点形成一个直观的印象,便于理解。
合作探究、发现原理:利用任务单进行任务驱动,学生小组合作探究,亲自动手操作,在操作与讨论过程中发现特征,得到结论。通过任务驱动可以更好地引导学生一步步进行探究,同时也可以激发学生学习的积极性;通过小组讨论,可提升学生团队协作意识。
角色扮演、加深理解:通过成果展示、学生讲解,让学生对探究过程进行梳理、总结,加深学生对该知识点的理解记忆。
6.重难点解决方案
以‘难点——无穷小的比较’为例:
程序1:x=-18:0.01:18; y=x.^2./(3.*x); plot(x,y,'r-','linewidth',2)
(2)算一算:利用matlab计算出x取0.1,0.01,0.001,0.0001,0.00001时,数趋于0的速度;
程序2:format long x=[0.1 0.01 0.001 0.0001 0.00001]
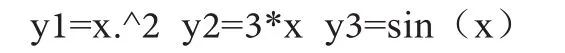
(3)讲一讲:小组代表讲解探究过程及结论;
(二)数值计算模块
1.知识点内容
各种类型函数的极限、导数、积分的计算。
2.设计原理
利用matlab的计算功能,变复杂为简单。
3.程序要求
教师介绍求极限、导数、积分的matlab命令格式,学生能够掌握计算命令,灵活利用命令进行求解,能够将求得的结果由matlab语言转换为数学表达式。
4.教学方法
主要采用软件辅助、分层教学和小组PK法。
5.设计意图
软件辅助、提高计算能力:学生在做题中虽然明确了解题思路,但因其基础知识掌握得不牢固,阻碍了计算,影响学生对问题的解决,打击了学生学习的积极性。matlab求极限、导数、积分等命令简单易掌握,适用范围广,可操作性强,可增强各层次学生的参与度,提升学生解决问题的广度和深度,提高学生的计算能力。
笔机结合、提升综合能力:设置笔算和机算两种形式的练习题,笔算的目的让所有层次的学生掌握解决该类型题的思路,能够计算基础的、简单的类型题,培养学生的思维能力,提高学生分析问题的能力;机算的目的是使各层次的学生都能够进行计算问题的求解,增强他们学习的兴趣,提升他们的自信心,提高他们解决问题的广度、深度和速度,使他们在以后的工作中能更好地、更高效地应用[3]。
分层教学、提高学生参与度:题目的难度逐层递增,小组成员根据自身的能力选择合适的问题进行解答,以接力赛的形式,培养学生团队协作意识、责任意识,实现了分层教学,使所有的学生都能参与进来,体会成功的喜悦。同时通过组间PK,提升学生的竞争意识。
6.重难点解决方案
以‘难点——求函数的极限’为例:
(1)引导分析:引导学生分析函数的特征,探究相应的解决方法;
(2)命令介绍:介绍求极限的matlab命令;

命令 功能syms x; 建立符号变量x limit(f,x,a)images/BZ_25_1984_440_2149_529.pnglimit(f,x,inf)images/BZ_25_1984_535_2149_624.png
(三)数学建模模块
1.知识点内容
生活案例:马尔萨斯人口增长模型,餐厅就餐模型,设备折旧费,流行病问题,生猪屠宰,复合的伤口,汽车行驶路程,公园的大小,排污水泵的规格等;
专业案例:建筑物的高度,钢梁长度的变化率,火车方向的改变率,悬臂梁的曲率,汽车对桥的压力,横梁的强度,列车的制动时间,抽水做功,钢索桥的长度等。
2.设计原理
利用matlab的数据处理、计算、画图等功能,化理论为应用。
3.程序要求
通过教师引导分析,能够制定实际问题的matlab解决方案
4.教学方法
主要采用小组讨论法、任务驱动法、实战演练法。
5.设计意图
实战演练、提升应用能力:用所学的理论知识来解决实际问题,将实际问题数学化,建立实际问题的数学建模,教师对建模的流程进行讲解,对案例进行分析提示,发布模型分析单,让学生小组讨论、查阅资料,利用matlab进行模型的建立与求解。通过成果展示汇报,教师点评,小组互评,选出最优解决方案。建模环节,帮助学生培养数学的思考方式,提高解决实际问题的能力,达成专业培养方案要求[4]。
6.实际案例解决方案
(1)教师对建模的过程和步骤进行讲解;
(2)介绍问题背景,引导学生分析案例;
(3)小组讨论,建立数学模型,利用matlab进行数据处理、数值计算或模型检验,完成模型分析单的填写;
(4)小组代表汇报,展示解决方案,教师点评,指出方案的优缺点。
高等数学的matlab模块化设计,可以有效地解决高职数学的教学现状,提升学生的学习效果。在实际教学中,通过不断的反思与改进来优化模块设计,使得模块的内容更合理,方法的设计更有效。
