特高压盾构管廊SF6泄漏模拟与通风系统优化
2021-04-01肖国锋何娜萍
肖国锋,何娜萍
(中国能源建设集团广东省电力设计研究院有限公司,广东 广州 510663)
近年来,直流输电技术发展迅速,中国的超高压和特高压直流输电技术发展走在世界前列。气体绝缘金属封闭输电线路(gas insulated transmission line,GIL)具有传输容量大、损耗小、占地少、可靠性高、对环境影响小等显著优点,其在地下管廊中的应用越来越广泛。GIL普遍采用SF6进行气体绝缘[1-2],当GIL管内充注高压SF6气体时,存在由于设计、制造及安装隐患等引发SF6气体泄漏可能性[3-5]。
SF6是一种无色无味气体,密度约为空气的5倍,是典型的重质气体。地下管廊属于封闭型地下构筑物,当GIL管发生事故破裂时,SF6气体会大量泄漏,高浓度SF6气体会造成人员窒息等安全事故发生[6]。当管廊SF6泄漏事故发生时,人体安全逃生方向判定、高浓度SF6泄漏区域设计控制即人体安全逃生距离设计等问题为人体安全逃生设计带来一定挑战。
图1所示为具有6 km跨度、包含上腔和下腔的特高压GIL盾构管廊,本文以此为例,研究恶劣泄漏条件下,管廊内SF6泄漏扩散过程以及侧吸、下腔通风系统开启后,上、下腔通风系统对SF6吸收和排出的能力,并根据人体安全逃生要求对SF6泄漏通风系统进行相应设计及优化。

图1 特高压盾构GIL管廊截面图Fig.1 Cross section of UHV GIL shield tunnel
1 SF6泄漏事故通风系统及影响因素
1.1 SF6泄漏事故通风系统
本文特高压GIL盾构管廊[7]包含上、下腔结构,其中上腔通风方案设计考虑GIL的发热、巡视工况;侧吸和下腔通风方案设计考虑泄漏气体吸收和排放。管廊系统通风运行方案如图2所示,在泄漏事故发生后,侧吸、下腔风机系统开启,建立SF6泄漏气体吸收和排出条件。图2中虚线箭头示意侧吸、下腔通风风机运行时的气体运动方向,实线箭头示意上腔通风系统运行时的气体运动方向。
1.2 SF6泄漏事故主要影响因素
用于表征泄漏口大小的物理量,工程中普遍采用孔径[7]的概念,本文引用该定义。GIL管内充注高压SF6,工作压力基本介于0.4~0.5 MPa,本文设计确定为0.5 MPa。因此,具有初始压力的SF6在泄漏口内、外压差的推动下,在泄漏位置边界处将GIL管内SF6的压能迅速转化为动能,获得速度并在自身流动物性影响下,在管廊内快速扩散。扩散受到管廊内部结构及通风条件的影响,逐步向下游扩散,最终排出管廊。总的来看,泄漏气体在管廊内的扩散过程受泄漏源性质、泄漏源初始压力、泄漏量、有限空间内风速风向、障碍物等的影响[8]。

图2 特高压盾构GIL管廊SF6泄漏事故通风运行方案Fig.2 Ventilation operation scheme for SF6 leakage accident in the UHV GIL shield tunnel
丁宗果[9]等人对水电站地下气体绝缘金属封闭开关(gas insulated metal closed switchgear,GIS)电缆层SF6泄漏扩散规律及通风设计进行了相关试验与数值模拟,系统研究了电缆层内SF6体积分数与排风量(试验平均风速范围为1.0~5.4 m/s)、排风口位置、泄漏量等因素的关系,得出以下结论:
a)正常泄漏时,SF6泄漏所产生的混合气体对排风机的性能和功率的影响十分微小,可以忽略不计。
b)事故排风量越大,电缆层内最大SF6体积分数越小,且衰减速度越快;当排风量达到一定程度后,继续增大排风量,SF6体积分数降低幅度不再明显。
c)通风模式下,SF6具有可完全排出系统外的排风设计条件,SF6体积分数降低到0所需时间随排风量增大而递减。
d)排风口位置对电缆层内SF6体积分数的分布影响较大,排风口距离泄漏点位置越近,影响越大。
e)从防治SF6污染的通风效果和节约能源的角度考虑,存在较经济排风口和排风量设计的可能。
2 数值模型建立
2.1 三维数值计算模型建立
2.1.1 计算基本假设
为模拟SF6从GIL管泄漏口泄漏到空气的过程及扩散过程,作如下计算假设:①SF6与空气的混合物为理想气体,符合理想气体方程;②SF6泄漏速度由初始压力、泄漏孔径决定,过程中SF6不与管廊内中的气体发生化学反应;③SF6在泄漏过程中为湍流流动状态;④通风方案设计时,取入口温度为30 ℃,廊内最大允许40 ℃限值,廊内SF6流动物性参数取35 ℃平均定性温度;⑤管廊截面形状始终保持一致。
2.1.2 流动控制方程
对于本文所研究的SF6在空气中的扩散流动问题,主要遵循质量守恒定律、动量守恒定律、能量守恒定律和组分守恒定律,这4个规律相应的控制方程分别如下。
a)连续性方程。质量守恒定律为单位时间内,流体微元体表面流入质量的总和等于微元体质量的增量,由此可得流体连续性方程为
(1)
式中:ρ为密度;t为时间;u、v、w分别为速度矢量V在x、y、z方向上的分量。
b)动量方程。动量守恒定律为单位时间内流体微元体动量的变化率为该微元体所受外界力之和,表达式为
(2)
式中:p为压力;τ为黏性应力;F为体积力;下标表示平面方向。
c)能量方程。能量守恒定律为单位时间内,流体微元体能量增量等于进入微元体的热流量加上体积力和表面力对流体微元体所做的功,表达式为
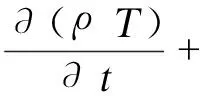
(3)
式中:cp为比热容;T为温度;k为传热系数;ST为黏性耗散。
d)组分方程。组分守恒定律为单位时间系统内某化学组分质量变化等于该组分通过系统表面的净流量及化学反应产生的该组分质量之和。本文所研究内容不包含气体之间的化学反应,因此忽略化学反应一项。组分s的组分方程为

(4)
式中:cs为组分s的体积密度;Ds为扩散系数。
2.1.4 计算边界条件假设
结合本文研究对象的特点及物理过程,计算中对模型的边界进行如下设置:①管廊壁面采用wall边界;②管廊进、出口采用速度或压力边界;③管廊内空气设置温度、速度边界条件;④SF6泄漏源采用初始压力或速度边界。
2.2 1D、3D扩散及流动数值模型计算对比
1D计算流体动力学(computational fluid dynamics,CFD)模拟具有计算速度快的特点,但对内部结构的流动特性缺乏详细解析;3D CFD模拟具有内部流动特性解析精度高的优点,但存在对于大跨度盾构管廊计算相对耗时的缺点。为实现千米级、大跨度特高压盾构管廊SF6的扩散模拟,结合SF6扩散的时域特点,采用“1D+3D”CFD耦合模拟的思想,对泄漏口附近的复杂扩散区域进行详细Fluent模拟,对扩散形态稳定后,随通风条件向下游推进段采用Flowmaster进行模拟,进而实现对6 km大跨度尺度下整体管廊SF6扩散的模拟。针对图1中的特高压盾构管廊结构,计算对比Flowmaster和Fluent在管廊压降和泄漏源泄压过程中压力随时间变化的相对误差。计算条件分别见表1、表2和表3。

表1 SF6泄漏气体在t=0时的状态Tab.1 SF6 leakage gas state at t=0

表2 盾构管廊气体在t=0时的状态Tab.2 Gas state in the UHV shield tunnel at t=0

表3 盾构管廊流阻计算对比参数设置Tab.3 Parameter settings for flow resistance calculation
2.2.1 压力平衡时间计算对比
利用Flowmaster元件库相关元件设置表1、表2对应的边界条件,获得图3所示的1D Flowmaster流动计算模型。利用3D CAD建模并完成网格剖分,设置相同的边界条件,获得图4所示3D Fluent流动计算模型。

图3 Flowmaster计算模型Fig.3 Flowmaster calculation model
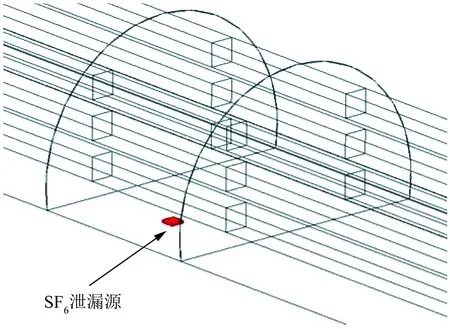
图4 Fluent计算模型Fig.4 Fluent calculation model
分别对图3和图4模型完成计算,获得如图5所示泄漏口出口压力随时间变化的结果。计算结果表明,对于盾构管廊,采用相同的边界设置条件下,Flowmaster和Fluent获得的计算结果高度一致。SF6泄漏源大气压力平衡时间对于管廊SF6泄漏事故的处理十分重要。Flowmaster完成模型单次计算所需时间为分钟级别,Fluent模型完成单次计算所需时间为小时级别,计算速度二者差别约为200倍。因此,充分利用Flowmaster的计算高效性,可快速获得不同泄漏口直径条件下的SF6泄漏源的大气压力平衡时间。

图5 泄漏源压力随时间变化计算对比Fig.5 Calculation comparisons of leakage source pressure varying with time by using Fluent and Flowmaster
2.2.2 管廊流阻特性计算对比
分别对上述模型建立边界条件(见表3),当管廊壁面粗糙度为3 mm、风速为5 m/s时,Fluent模型计算获得管廊上层结构6 km的等效压降为708 Pa,Flowmaster模型计算获得管廊上层结构6 km的等效压降为732 Pa,二者相对误差为3.28%。
计算结果表明,无论对于泄压时间还是管压降计算,2个模型对于具有统计意义的参数能够获得较为一致的计算结果。更进一步地来说,对于大跨度盾构管廊泄漏模拟,采用“1D+3D”耦合分析模型在耦合界面处具有良好的压力和质量流量耦合条件,具备满足“1D+3D”耦合分析的完备条件。
2.3 1D、3D耦合流动模型建立
采用数值模拟计算方法模拟SF6扩散[10-11],建立如图6所示的基于Flowmaster和Fluent的“1D+3D”耦合分析模型,用于计算泄漏发生后的扩散情况,并考虑侧吸、下腔通风系统开启后,SF6气体的吸收和排出情况。
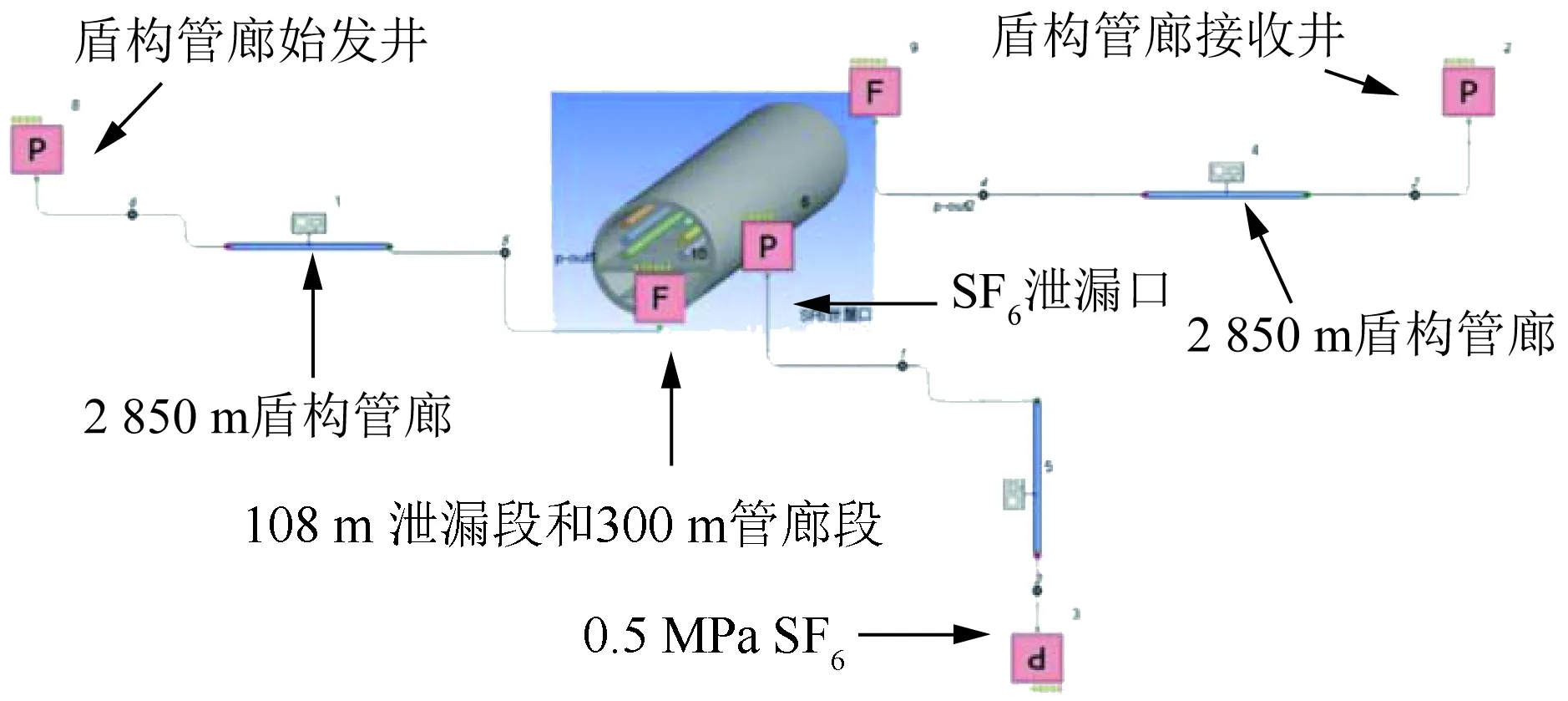
图6 盾构管廊“1D+3D”耦合模型(全长6 km)Fig.6 “1D+3D” coupling model of shield tunnel (6 km length)
本设计中,取GIL管单个气室长度为108 m,计算假设泄漏发生在GIL管廊中部,泄漏口位于管廊一侧、距离上腔地面位置最近的GIL管气室内。SF6初始压力为0.5 MPa,泄漏口水力直径为125 mm,SF6初始气温为80 ℃。廊内空气取35 ℃。耦合分析模型中,用于3D Fluent模型计算的管廊长度为300 m,泄漏口位于该段管廊中部,即泄漏口距离3D模型两侧各150 m。由于管廊截面尺寸较大,空气与SF6形成的混合气体中SF6占比较小,SF6对整体通风流动阻力的影响较小,忽略坡度(设计小于2°)和管廊线型的影响,其余两侧管廊采用长度各为2 850 m直线管段,考虑单一空气或混合气体流动压降的影响,并采用Flowmaster气体元件进行建模。在1D、3D模型的流动边界处,建立压力及质量流量等耦合边界条件,上、下腔通风系统两侧取大气边界条件。
3 SF6安全浓度限值与通风建立时间计算
DL/T 639—2016《SF6电气设备运行、试验及检修人员安全防护细则》及GB/Z 2.1—2019《工作场所有害因素职业接触限制》规定,室内六氟化硫气体含量不得超过1 000 μL/L(质量分数为5 000 mg/kg),氧气含量不应低于18%。如果气体浓度超标,电气设备检修人员无法进入管廊中,应对相应故障进行快速有效处理。
影响下腔通风系统开启时间的主要因素包括:SF6泄漏到报警装置触发所需时间、报警装置触发风机开启的延迟时间、隧道风机达到额定转速所需时间、流动建立所需压差建立时间等。本文假设相关子过程完成时间计算建立在监控点间距20 m、上腔风速为5 m/s的条件下。距离泄漏发生后下腔通风系统开启各子过程时间分别为:报警触发4 s,风机开启延迟1 s,隧道风机开启到平稳所需时间为10 s,流动建立10 s。累计所有子过程时间,即当SF6开始泄漏到下腔风机建立下腔通风系统平稳流动所需时间为15 s。
4 数值模拟结果分析与讨论
SF6为重质气体,泄漏发生时,具有其自身的特点[12]。当SF6泄漏后,盾构管廊内上腔通风系统始终保持运行通风是常见通风处理方法[13],为加快泄漏气体[14-15]排放,计算取设计允许最大风速5 m/s。以下针对此类通风运行模式,进行泄漏气体扩散过程模拟。根据图6建立全管廊“1D+3D”耦合模型[16-19],计算条件设置同上述分析所设置条件,分别模拟下腔不同通风风速下[20]的泄漏扩散过程。
4.1 管廊下腔通风系统关闭时泄漏扩散模拟
泄漏发生后,若下腔管廊通风系统始终关闭,计算模型对应下腔风速设置为0,此时,SF6扩散运动形态及区域浓度分布计算结果如图7、图8所示。
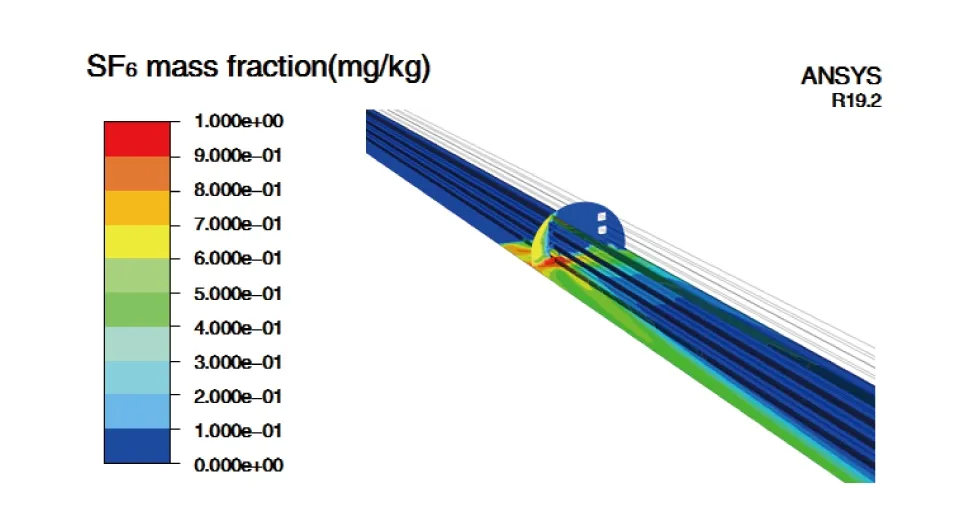
图7 泄漏t=14 s管廊SF6质量分数分布(5 m/s通风风速)Fig.7 SF6 mass concentration distribution at t = 14 s and 5 m/s ventilation speed
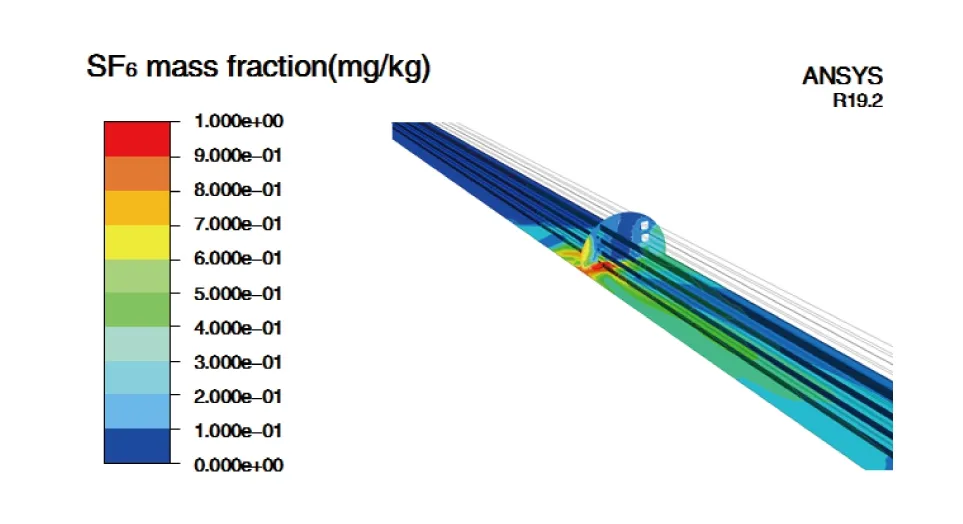
图8 泄漏t=115 s管廊SF6质量分数分布(5 m/s通风风速)Fig.8 SF6 mass concentration distribution at t = 115 s and 5 m/s ventilation speed
图7计算结果表明:泄漏事故发生14 s后,受泄漏初速度及迎面风速的共同影响,SF6从泄漏口沿背风面扩展到下游150 m左右位置,此时,无论下腔风机是否开启,距离泄漏口150 m为理论最短控制区域。图8计算结果表明:当管廊下腔通风系统始终不开启时,SF6在通风作用下,逐步向管廊下游出口方向进行扩散,115 s后管廊上腔部分区域SF6体积分数下降到低于1 000 μL/L(质量分数为5 000 mg/kg)的安全数值范围内。
由此可见,当且仅当工作人员距离泄漏口较近且能够向迎风面撤离时,才可能取得安全撤离条件。由于泄漏发生前,无法确定泄漏发生位置,因此,GIL盾构管廊存在较高的泄漏事故发生后的人体安全撤离风险[21-22]。
4.2 泄漏15 s后扩散区域不扩大时的通风设计
考虑到泄漏发生后,下腔结构通风条件的完整建立需要一定时间,要取得扩散区域不向背风方向继续下游扩散的技术条件为:15 s后,下腔通风条件建立后,能够完全吸收已经泄漏出的SF6气体。故按此要求对SF6侧吸风机数量、风量或风机选型进行设计。经过反复计算,当管廊下腔平均风速不小于3 m/s时,能够满足该技术条件。图9—图11所示为不同时刻SF6高于安全限值的区域分布情况。

图9 泄漏t=15 s管廊SF6质量分数分布(5 m/s通风风速)Fig.9 SF6 mass concentration distribution at t = 15 s and 5 m/s ventilation speed
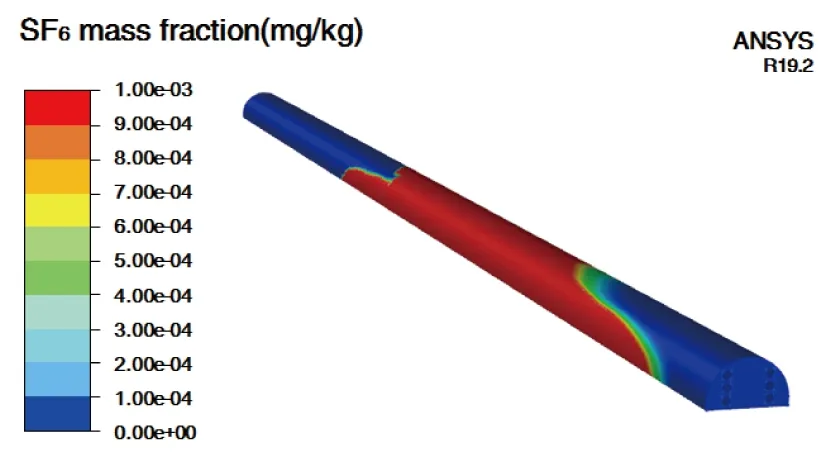
图10 泄漏t=20 s管廊SF6质量分数分布(5 m/s通风风速)Fig.10 SF6 mass concentration distribution at t=20 s and 5 m/s ventilation speed
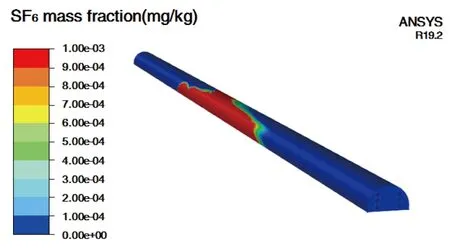
图11 泄漏t=55 s管廊SF6质量分数分布(5 m/s通风风速)Fig.11 SF6 mass concentration distribution at t=55 s and 5 m/s ventilation speed
以上计算结果表明:当泄漏发生15 s后,侧吸及下腔通风风机开启后,泄漏区域SF6立即得到吸收,并不向下游进行扩散;55 s后,随着SF6泄漏流量持续下降,SF6高浓度区域趋于稳定收缩状态。此时,侧吸风机设计结果为:单个气室108 m范围内,管廊双侧对称布置侧吸风机,间隔30 m布置1台;侧吸风机风量不低7 200 m3/h,全压不小于300 Pa;6 km管长合计双侧共布置400台侧吸风机。
4.3 泄漏15 s后上腔通风系统关闭条件通风设计
当管廊上腔通风系统始终保持运行条件时,由于上腔风速对SF6有推动作用,增加了对侧吸风机的配置需求。泄漏报警后,随即关闭上腔通风系统,能够降低对侧吸风机的配置需求,故本节依此条件,对侧吸风机进行优化设计。计算条件同上述条件设置,忽略泄漏监控点距离泄漏源的距离,并假设报警后,管廊上腔通风速度立即降低为0 m/s。
泄漏发生15 s后,侧吸及下腔通风风机开启、上腔通风立即关闭后,计算结果表明,泄漏区域SF6吸收能力较上腔通风系统保持开启时显著增强。图12、图13所示为相应计算结果。计算结果显示,泄漏发生20 s后,体积分数高于1 000 μL/L(质量分数为5 000 mg/kg)的区域快速收缩到距离泄漏口位置65 m范围内。

图12 泄漏t=20 s管廊SF6质量分数分布(0 m/s通风风速)Fig.12 SF6 mass concentration distribution at t=20 s and 0 m/s ventilation speed
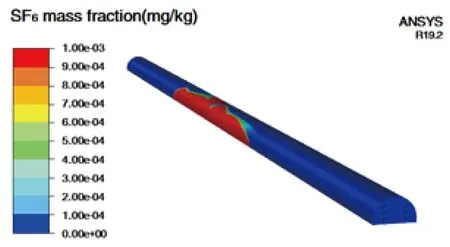
图13 泄漏t=55 s管廊SF6质量分数分布(0 m/s通风风速)Fig.13 SF6 mass concentration distribution at t=55 s and 5 m/s ventilation speed
满足上述计算结果的侧吸风机设计结果为:单个气室108 m范围内,管廊双侧对称布置侧吸风机,间隔30 m布置1台;侧吸风机风量不低于4 800 m3/h,全压不小于300 Pa;6 km管长合计双侧共布置400台侧吸风机。
泄漏发生时,相较于上腔通风系统始终开启条件下,泄漏报警后上腔通风系统立即关闭通风,侧吸风机系统的风量需求降低38%,泄漏发生20 s后管廊内SF6体积分数高于1 000 μL/L(质量分数为5 000 mg/kg)的区域长度从135 m缩短到65 m,降低了52%。
5 结论
本文采用数值模拟技术研究了特高压盾构管廊SF6泄漏数值模拟与通风系统优化,主要结论如下:
a)建议通过侧吸通风方式将SF6泄漏气体从管廊上腔引导到下腔并通风排出,降低泄漏发生时存在的人体安全撤离风险系数;
b)侧吸通风具体布置及通风量设计是影响SF6在管廊内气体浓度分布的重要因素;
c)采用具有上、下腔结构的盾构管廊结构,泄漏发生时,上腔通风始终保持开启条件下,缩短侧吸及下腔通风系统流动建立时间,设计合理的SF6侧吸、排放通风方案有利于对管廊内SF6高浓度区域进行控制;
d)泄漏发生后,上腔通风系统关闭更有利于进一步缩短人体安全撤离距离,同时能够有效降低侧吸风量设计需求。
