基于星型零电流开关电容的电压均衡电路
2021-04-01廖武兵陈渊睿刘润鹏
廖武兵,陈渊睿,刘润鹏
(华南理工大学 电力学院,广东 广州 510641)
随着全球变暖和化石燃料的消耗,节能和环保引起了全世界各个国家的高度重视[1-2],世界各国也因此对清洁能源技术展开深度研究。作为能源项目的核心,储能技术是解决可再生能源间歇性供电问题的有效方案。随着储能技术的高速发展,它被广泛地应用于各个领域,如电动汽车、微电网和可再生能源系统等[3-9]。作为储能系统的核心组成部分,储能元件的使用在很大程度上决定了储能系统运行的性能、安全性及其制造成本。目前储能元件主要有2种:超级电容和锂离子电池。因单体电压等级较低,储能系统通常由大量电池或超级电容串联而成。而单体间特性的不均匀性,导致电池组或超级电容组每个单体的端电压在使用过程中逐渐变得不一致,经过长时间的充放电积累,组内电压不平衡越发严重。另外,由于使用过程中储能元件的温度分布也可能不同,会进一步导致储能单体间的差异,加重单体工作电压的不平衡[10]。文献[11]提出,储能元件的电压不平衡导致了储能系统运行过程中容量利用率的降低和潜在的过充电或过放电。对于电池和超级电容来说,过充电和过放电会影响其使用寿命,甚至直接使电池和超级电容性能恶化而引发爆炸等危险;因此,电压均衡电路对串联的电池组或超级电容组是必不可少的,它能保证储能系统安全稳定地运行[11-12]。
现有的均衡策略分2种:被动均衡和主动均衡。被动均衡主要为并联电阻式,每个储能单元都并联1个电阻,通过电阻来消耗掉多出的能量并实现电压均衡[13]。该方法结构简单,但存在能量利用率低、发热大的问题。主动均衡可分为基于电感器[14-17]、基于变压器[18-21]和基于电容器[22-29]的方法。基于变压器的均衡电路通常需要体积庞大的磁性元件在电池之间传递能量,因此电路的体积大,成本高,质量大。基于电感器的均衡电路需要额外的电压检测电路,来对每个电池或超级电容单体进行闭环控制,需要较为复杂的电路结构和控制策略。与以上两者相反,由于没有任何磁性部件,且只需要1对固定频率和占空比的互补脉冲宽度调制(pulse width modulation,PWM)信号,基于开关电容的均衡器具有尺寸小、成本低、控制简单和可靠性高等优点。
文献[22]提出了基于开关电容的电压均衡电路,电路中电容是以阶梯的形式排列,由于单体间的能量只能利用阶梯电容在2个相邻电池间进行传递,因此所提电路的均衡性能总是随着电池单元数量的增加而下降。为了加速电池均衡过程,文献[23]提出了基于双层开关电容的均衡电路,它在第1个和最后1个单元之间提供1条能量传递路径,加快了均衡的速度;然而,这种改进开关电容电路并没有从根本上解决能量只能在相邻单体传递的问题,它们的平衡速度仍然随着储能单体数量的增加而下降。针对这个问题,文献[24]提出了一种改进的开关电容电压均衡电路,在电路元器件无显著增加的情况下,电路可实现电压均衡速度与均衡单元数量的解耦,以提高均衡速度。然而,上述基于开关电容的均衡电路都工作在硬开关状态下,在开关过程中,电容的电流尖峰会引起电磁干扰和增加开关损耗。为了克服这个问题,文献[25-27]分别引入了基于阶梯、双层和delta结构零电流开关电容的均衡电路,使得所有开关都在零电流开关下工作。但阶梯和双层结构电路均存在均衡速度总是随着电池单元数量的增加而下降的缺点,而delta型结构导致系统存在电路体积大、电容电压应力过大和模块化困难等缺点。
针对上述拓扑存在的问题,本文提出一种基于星型零电流开关电容的电压均衡电路。该电路可解决现有电路中均衡速度总是随着储能单元数量的增加而下降、硬开关导致损耗增加、不易于模块化、电路体积过大等问题。
1 星型零电流开关电容电压均衡电路
1.1 电路工作原理
本文所提出的基于星型零电流开关电容的电压均衡电路如图1所示,图中B1、B2……Bk为各储能单元,S1、S2……S2k为与储能单元并联的开关管,C1、C2……Ck为各电容器,L1、L2……Lk为各电感器。

图1 本文提出的星型零电流开关电容电压均衡电路Fig.1 The proposed voltage equalization circuit based on star structured zero-current switched capacitor
与常规基于开关电容的电压均衡电路一样,每个串联的储能单体与2个互补导通的金属-氧化物半导体场效应晶体管(metal oxide semiconductor field effect transistor,MOSFET)并联[22-27]。能量传递模块是由电容器和电感器组成的准谐振槽,所有电容器和电感器的一端都连接在一起,另一端接入每对MOSEFT的中点,故称其为星型结构。电路通过星型能量传递模块和开关管的切换,将能量从端电压较高的储能单体转移到端电压较低的储能单体。
电压均衡电路的模态如图2所示。假设:电路中各电容的值相同,均用C表示;各电感的值相同,均用L表示;各储能单元电压UB1>UB2>…>UBk。

图2 本文提出电压均衡电路的2种工作模态图Fig.2 Two operation modes of the proposed voltage equalization circuit
为了便于计算,将电路的时域变换为频域,每个回路的等效频域电路如图3所示,图中s为复数频率。假设:每个谐振回路的直流电阻(包括电容、电感和MOSEFT的寄生电阻)的值相同,均用R表示;每个电容器上的电压相同,均用UC表示。以第1个单元到第k-1个单元向第2个单元到k个单元传递能量为例,进行模态分析。
模态A:此模态下,奇数开关管开通,偶数开关管关断,如图2(a)所示。根据图3的频域电路图,

图3 等效频域运算电路Fig.3 Equivalent frequency-domain operational circuit
以第1个单元到第k-1个单元为例,由KVL定律列出电容电压和电流频域表达式:
(1)
式中UC1,min、UCk,min为电容器C1、Ck在模态A开始时的电压值,即最小值。
将I(s)和U(s)分别进行Laplace反变换,得到如下时域表达式:
(2)
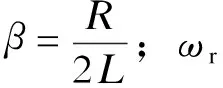
若开关周期等于谐振周期,经过半个谐振周期后,即当t=π/ωr时,流过开关管的电流IS(t)为0,开关管实现了零电流关断。而此时电容器C1、Ck两端的电压达到最大值UC1,max、UCk,max,其表达式为
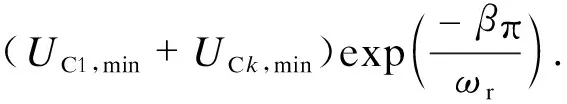
(3)
模态B:此模态下,偶数开关管开通,奇数开关管关断,如图2(b)所示。同理于模态A,以第2个电池到第k个电池为例,由KVL定律列出电容电压和电流频域表达式:
(4)
将I(s)和U(s)分别进行Laplace反变换,得到如下时域表达式:
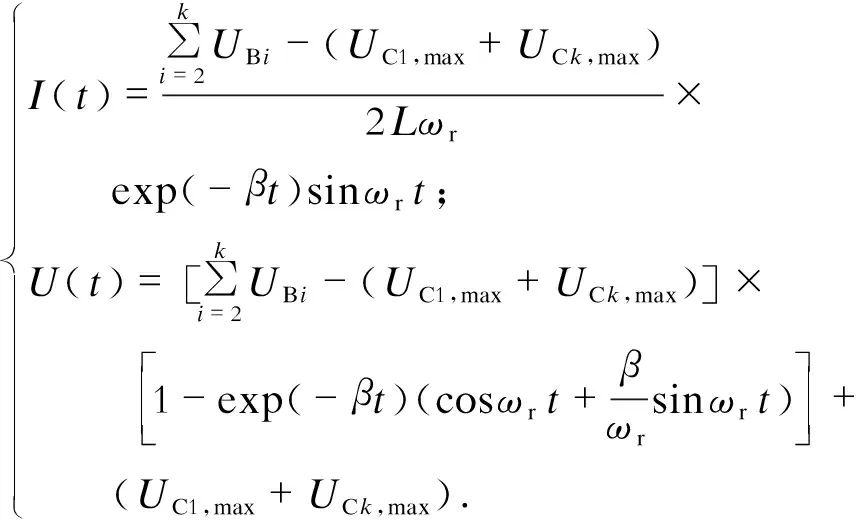
(5)
同样地,经过半个谐振周期后,开关管实现了零电流关断。而此时电容器C1、Ck两端的电压达到最小值,其表达式为

(6)
上述2种工作模态交替工作在高开关频率下,使能量从电压较高的单体自动流向电压较低的单体。在所提出的均衡电路中,所有RLC谐振回路都具有相同的工作原理,并且所有开关都在零电流下开通和关断,减少了整个均衡系统的损耗。
1.2 均衡分析
根据式(3)和式(6),可以得到在1个均衡周期中电容电压的变化量ΔUC,
ΔUC= (UC1,max+UCk,max)-(UC1,min+UCk,min)=

(7)
在1个开关周期内,根据电容电压的变化量可以计算出单个回路的平均电流Iavg,
(8)
式中fS为开关频率。因此,可以计算出每个均衡回路的等效电阻RSC,
(9)
由于星型结构中每2个单体间的电容器都是互用的,每2个储能单元构成的回路中的等效电阻为RSC但不互相独立,因此将RSC拆分为2个独立的等效电阻RSC/2,最终等效电路图如图4所示。
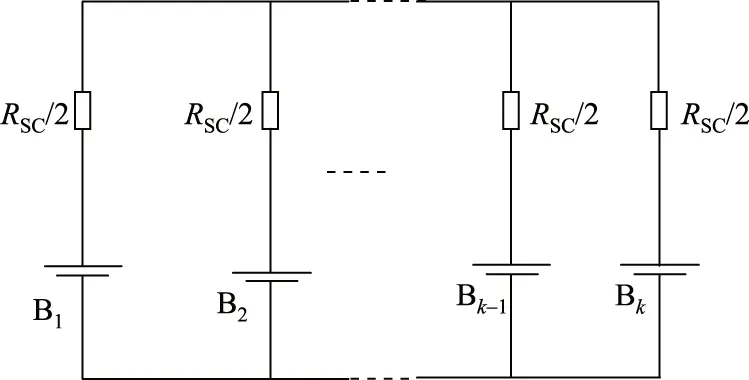
图4 等效均衡电路Fig.4 Equivalent equalization circuit
根据等效电路图,星型能量传递结构能提供能量直接从任意高电压的单体转移到任意低电压单体的均衡路径,这也意味着所提拓扑具有更快的均衡速度,而且均衡速度不再受限于参与均衡的储能单元的数量。
1.3 能量转化效率分析
在电压均衡系统中,能量转换效率被定义为储能系统均衡后和均衡前能量的比值[28]。在不考虑能量转移模块中小电容少量电荷损耗、开关管损耗的情况下,根据电荷守恒定律,基于开关电容的电压均衡电路最终的均衡电压Ubal可以表示为
(10)
因此,电压均衡系统的理论效率
(11)
式中:UBi,start为均衡前单体的电压;Estart、Eend分别为均衡前后的能量。
但在实际应用中,开关损耗是不可忽略的,而且系统不可能将储能单体均衡到电压绝对一致的水平,而这也最终影响着均衡效率。实际效率
(12)
式中UBi,end为均衡后单体的电压。
本文所提电压均衡电路可实现开关管的零电流开通关断,降低开关电荷损耗,提高了均衡效率,使得系统的均衡效率接近于理论的均衡效率。
2 模块化设计
根据式(3)和式(6),星型结构中电容器的最大电压应力与串联储能单元的数量呈正相关。当串联的储能单元数量很大时,电容器的最大电压应力大,电容器体积随着增大,将会导致系统体积过大[24];因此,基于开关电容的电压均衡系统一般需要模块化设计来减少电压应力,常规的模块化设计就是在原本模块的基础上再加上相同的均衡电路[29],这种设计不仅会增加电路成本,而且电路可靠性大大降低。针对上述情况,本文提出一种模块化设计方案,如图5所示。
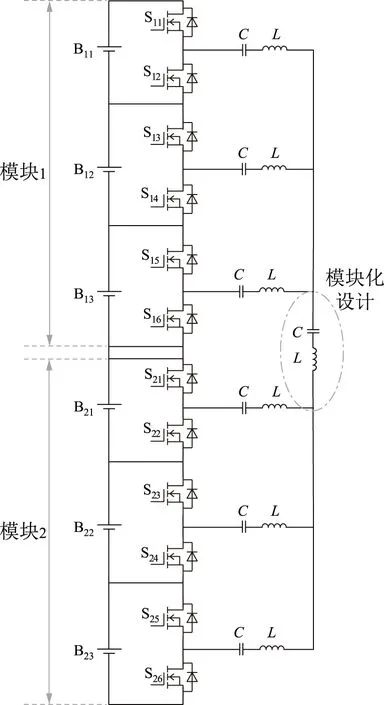
图5 模块化设计Fig.5 Modularization design
通过1个LC准谐振槽连接2个模块的星型模块的中点,模块间的单体通过3个LC准谐振槽进行能量传递。它的工作原理与单模块的均衡电路基本相同,并不影响电路的零电流开关;因此,在不增加开关管的基础上,这种方案实现了简单的模块化设计,节省了电路成本和体积。
3 实验验证
为验证所提电压均衡拓扑的可行性,搭建超级电容储能系统实验平台,如图6所示。储能元件为凯美200 F超级电容;开关管选用英飞凌IRF250N,开关频率为22 kHz;选取LC准谐振槽电容器的容值为10 μF,电感器的感值为4.7 μH。由TMS28335生成多路带死区的互补驱动信号,经过光耦TLP250驱动开关管,每对开关管的控制电路硬件设计如图7所示。实验采用新威CT-4008对各个超级电容进行充放电以及电压数据的记录。

图6 实验平台Fig.6 The experimental platform
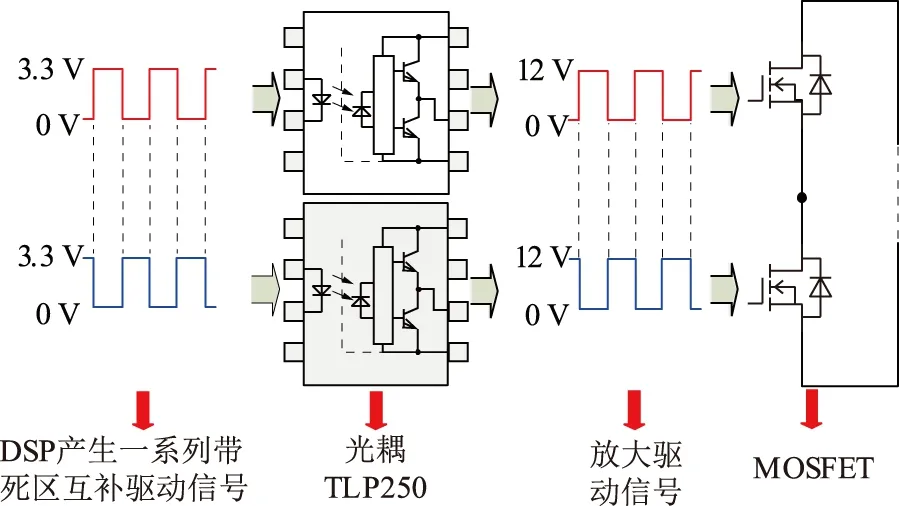
DSP—数字处理器,digital signal processor的缩写。
图8显示了所提拓扑在三单元均衡实验波形。3个超级电容在1 600 s后达到一致的电压水平,均衡电压约为2.008 V。
同样地,将拓扑运用在四单元的储能系统上,其实验波形图如图9所示。4个超级电容同样在1 600 s后达到一致的电压水平,均衡电压约为1.994 V。实验结果验证了在最大电压差一定的情况下,所提出的基于星型结构的电压均衡电路的均衡速度并不受单元数量的影响。
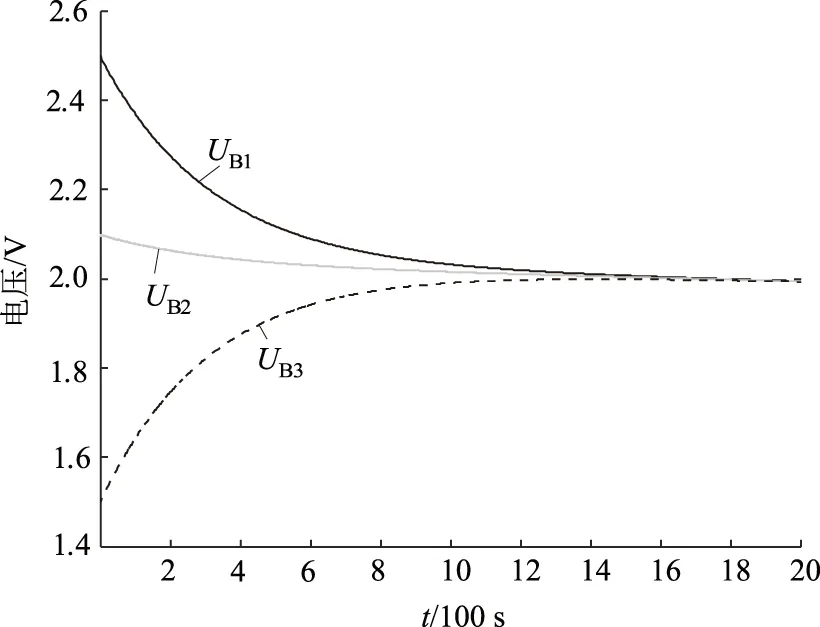
图8 三单元实验结果Fig.8 The experimental results of three cells
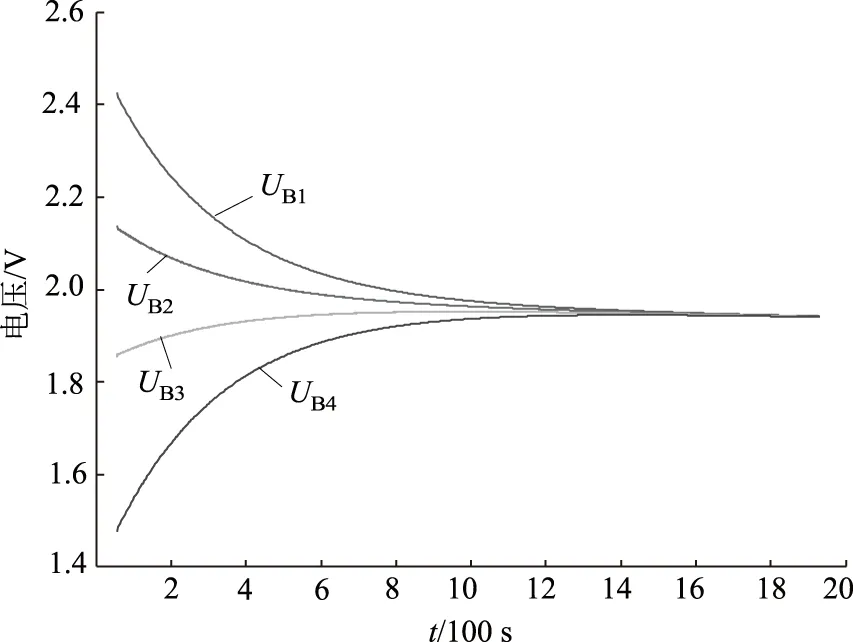
图9 四单元实验结果Fig.9 The experimental results of four cells
图10为2个三单元均衡拓扑的模块化实验结果。模块间各个超级电容大约在4 000 s后达到电压一致的水平(由于加入了额外的LC电路导致均衡路径变长,因此相对于非模块化设计,模块化设计的均衡时间较长),均衡电压约为2.201 V,单体间的最大电压差小于10 mV。实验结果验证了所提出的模块化设计的有效性。
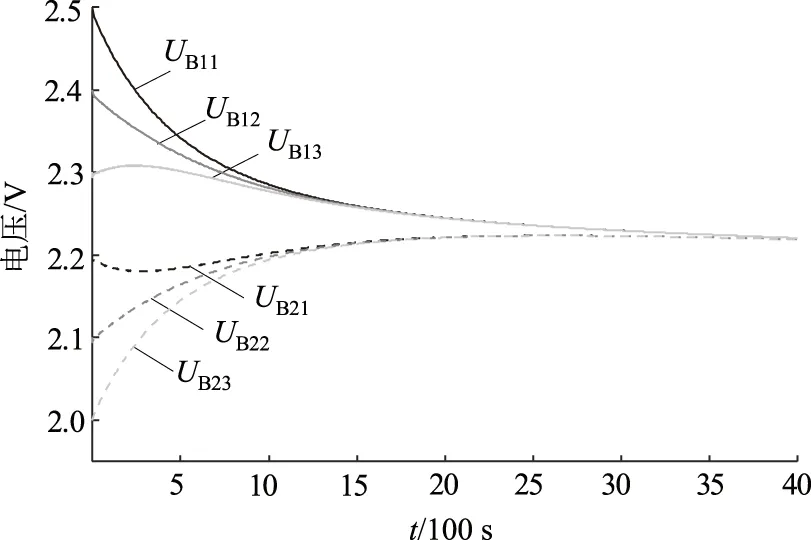
图10 模块化六单元均衡实验结果Fig.10 The experiment results of modularization equalization for six cells
图11为均衡过程中开关管电流IS的波形,电流呈正弦规律,在驱动信号UGS1、UGS2结束时达到0,实现了软开关,减少了均衡系统的开关损耗和电磁干扰。表1对3组实验结果进行了统计,并根据式(12)对均衡效率进行计算。3组实验的均衡效率均达到94%以上,证明了所提电路的高效率性。
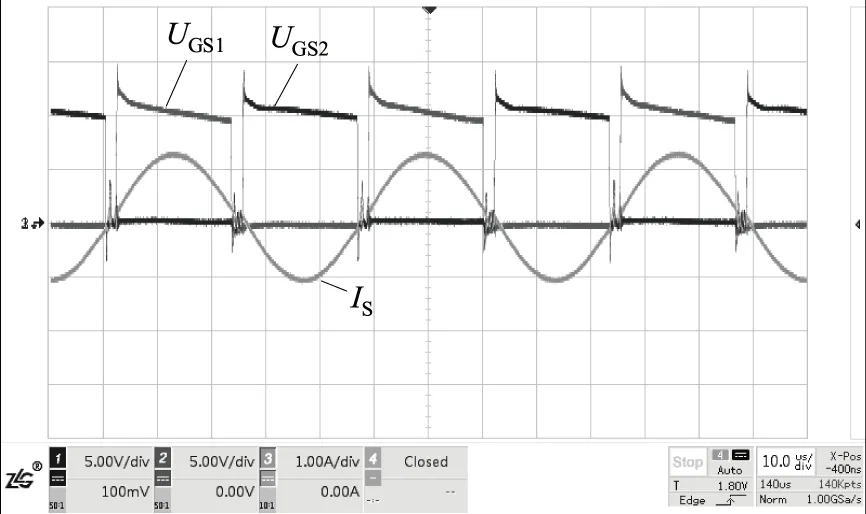
图11 开关电流波形Fig.11 Switch current waveforms

表1 实验结果对比Tab.1 Comparison of experimental results
4 结论
本文提出了一种基于星型结构零电流开关电容的电压均衡电路,分析并研究电路结构、均衡原理、能量转化效率和模块化设计,最终建立三单元、四单元、模块化六单元的实验样机进行实验验证。具体结论如下:
a)三单元和四单元的均衡时间均为1 600 s,证明所提出电路的均衡速度与均衡单元数量无关。
b)所提出的电路实现了零电流操作,减小了系统电磁干扰和损耗,均衡效率达94%以上。
c)通过LC准谐振槽将各个模块的星型结构中心相连即可实现模块化均衡,不需要额外的均衡结构,减少了模块化设计的成本和体积。
