非线性离散系统基于扩展Kalman滤波的鲁棒融合状态估计
2021-04-01马光鹏孙小君
马光鹏,孙小君,2,*
(1.黑龙江大学 电子工程学院,哈尔滨 150080;2.黑龙江省信息融合估计与检测重点实验室,哈尔滨 150080)
0 引 言
众所周知,在实际生活中非线性环节普遍存在,尤其是在各种定位系统中。通常状态方程是建立在笛卡尔坐标下的,观测方程是建立在极坐标下的,这使整个定位系统呈现一种非线性特质。处理这些非线性环节的方法为线性逼近。
多传感器信息融合[1]也称多传感器数据融合,是20世纪70年代以来由于战争及高科技领域的迫切需要发展起来的一门新兴边缘学科,目前已成为备受人们关注的热门领域[2]。第二次世界大战期间,人们就已经把两传感器数据融合应用于火炮系统,增强了系统抗干扰能力,目前国内外已经提出了诸多算法,有在最小二乘法和最小方差意义下的集中式分布和混合式融合算法[3-5],极大似然最优信息融合准则[6],加权观测融合估计算法[7]等,但是非线性系统的融合算法结构和估计性能很大程度上取决于所采用的局部滤波方法,如扩展 Kalman 滤波 (Extend Kalman fifilter, EKF)[8]、无迹滤波 (Unscented Kalman fifilter,UKF)[9]、粒子滤波 (Particle fifilter, PF)[10-12]和求容积滤波 (Cubature Kalman fifilter, CKF)[13]等。基于不同的局部非线性滤波器所获得同类融合算法的性能也存在差别。EKF算法有很多缺点和不足[14-19],它的近似线性化方法就是略去二阶以上Taylor级数展开式,大量信息被略去,这导致估计结果产生较大偏差。将针对这一问题进行研究。选择的CI融合算法不需要求解局部估计误差互协方差。提出的多传感器非线性系统的CI融合Kalman滤波算法将提高多传感器非线性系统的状态估计精度。仿真实验结果表明,所提出的非线性系统融合状态估计方法有效可行。
1 问题描述
离散非线性系统动态方程可以表示为
X(k+1)=f[X(k),k]+G(k)W(k)
(1)
Zi(k)=h[X(k),k]+Vi(k),i=1,…,L
(2)
当过程噪声W(k)和观测噪声Vi(k)恒为零时,系统模型的解为非线性模型的理论解,又称为“标称轨迹”,而把非线性系统的真实解称为“真轨迹”。
假设1过程噪声W(k)是均值为零的高斯白噪声,且矩阵G(k)是已知的。
假设2 观测噪声Vi(k)是均值为零的高斯白噪声,并且过程噪声W(k)和观测噪声Vi(k)相互独立。
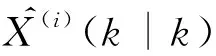
2 局部扩展Kalman滤波器

(3)
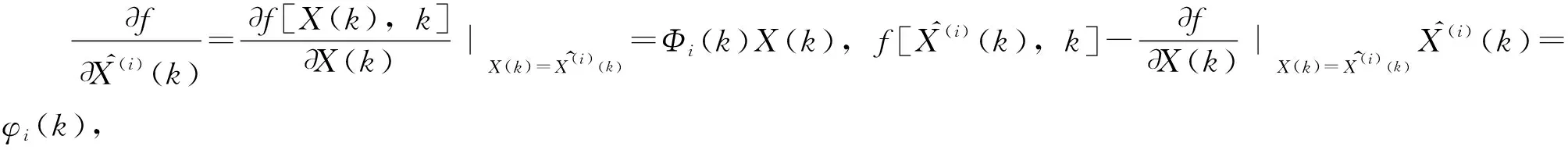
X(k+1)=Φi(k)X(k)+G(k)W(k)+φi(k)
(4)

(5)
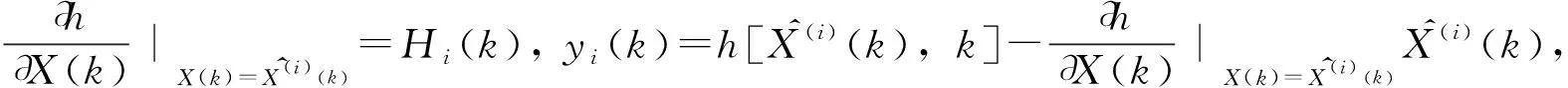
Zi(k)=Hi(k)X(k)+yi(k)+Vi(k)
(6)
由射影定理可知
(7)
(8)
对(5)式求射影定理得
(9)
引出新息表达式
(10)
记滤波和预报估值误差及方差阵为

(11)
(12)
(13)
(14)
则由式(6)和式(9)可得
(15)
由式(4)和式(7)有
(16)
(17)
由式(16)得到
(18)
因为
(19)
有
E[εi(k+1)X(i)T(k+1|k)]=0
(20)
于是由式(15)得新息方差阵为
(21)
根据式(17)得
(22)
因为
(23)
因为射影定理正交性
(24)
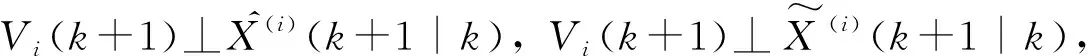
(25)
(26)
现在用Ki(k+1)的表达式简化Pi(k+1|k+1)得
Pi(k+1|k+1)=[In-Ki(k+1)Hi]Pi(k+1|k)
(27)
这是根据线性Kalman滤波基本方程[20]得到的扩展Kalman滤波递推方程[21-23]。根据上述推理则递推扩展Kalman滤波器如下:
定理1多传感器非线性系统(1)和(2),在假设1和假设2下,有局部扩展Kalman滤波器
(28)
(29)
(30)
(31)
(32)
Pi(k+1|k+1)=[In-Ki(k+1)Hi]Pi(k+1|k)
(33)
状态转移矩阵和观测矩阵由f和h的雅可比矩阵代替。假设状态变量有n维,即X=[x1x2…xn]T,则相应的雅可比矩阵的求法[24]如下:
(34)
3 鲁棒CI融合估计算法
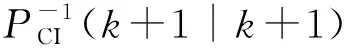
(35)
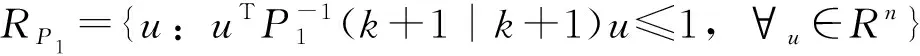
(36)
注意0≤ω≤1,则有
(37)
引出u∈R,故R⊃RP1⊃RP2成立,注意
(38)
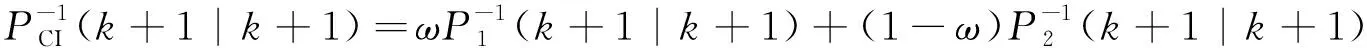
(39)
则R就是PCI(k+1|k+1)的协方差椭圆,即
(40)

(41)
(42)
(43)
(44)
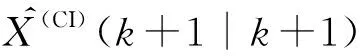
(45)
将式(42)代入式(43)和式(44)得到CI融合扩展Kalman滤波算法。通过上述文字描述和公式推理得到的CI融合算法如下:
定理2多传感器非线性系统(1)和(2),在假设1和假设2下,有CI融合扩展Kalman滤波器
(46)
(47)
4 仿真模型和结果分析
实验结果表明,当系统存在非线性环节时,使用局部线性化扩展Kalman滤波时有较大的误差,而在扩展Kalman滤波基础上在进行CI融合估计可以有效地降低系统误差,相较其他观测融合估计计算量较小且提高了多传感器的系统状态估计的精度。
考虑非线性阻尼谐振子模型[26],设X为二维向量,状态分量分别为位置(m)、速度(m/s)即X(k)=[x1(k),x2(k)]T,相应的两传感器非线性离散系统为
X(k)=f(X(k-1))+ΓW(k-1)
(48)
Zi(k)=HiX(k)+Vi(k),i=1,2
(49)
状态的真实值与局部和CI融合扩展Kalman滤波器的对比曲线见图1。由图1可见,CI融合有效提高了估计精度。
CI融合最优参数见图2,CI融合和局部滤波器的精度关系仿真见图3。在仿真程序的调试过程中,发现选取的系统参数不同时,图3的精度关系也会出现融合估计精度低压局部某个融合估计的情况,这也正是CI融合的鲁棒性所在。
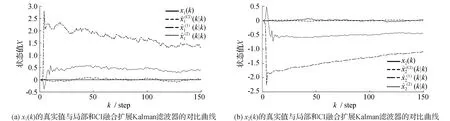
图1 状态X(k)=[x1(k),x2(k)]T的真实值与局部和CI融合扩展Kalman滤波器的对比曲线Fig.1 Comparison curve between the true value of X(k) and the local CI fusion extended Kalman filter

图2 参数ω的仿真Fig.2 Simulation diagram of parameter ω

图3 CI融合和局部滤波器的精度关系仿真Fig.3 Simulation diagram of the accuracy relation ship between CI fusion and local filter
5 结 论
本文对多传感器非线性离散系统提出了鲁棒CI融合扩展Kalman滤波算法。通过两传感器二维系统仿真实验表明,引入鲁棒CI信息融合算法提出的CI融合扩展Kalman滤波器有效提高了多传感器非线性系统的状态估计精度,且算法形式简单,便于工程应用。
