广域电力系统动态稳定性分析的时滞系统方法

赵亚文，丛 屾

(黑龙江大学 机电工程学院，哈尔滨 150080)

0 引 言

随着现代电力系统运行规模的逐步扩大，整个系统的动态过程也变得更加复杂，传统的控制方式已无法满足其动态性能指标的控制要求[1]。二次系统是保证电力系统稳定运行及电能质量的基本组成部分，特别是基于相量测量单元(PMU)的广域量测技术(WAMS)的发展推动产生了电力系统的全局化控制[2-4]。然而，在广域环境下(特别在远距离传输时)检测并控制系统的运行必然存在着测量和控制环节中的时间延迟现象。有研究表明，在这些环节中很小的时滞都有可能对整个系统的稳定运行造成致命影响[5-6]。因此，研究二次系统中的时滞对电力系统的稳定性的影响具有十分重要的理论与现实意义[7-8]。

就一般的时滞动力系统而言，稳定性分析方法主要可分为频域法和时域法。由于电力系统自身具有的参数不确定性及时滞的时变性，时域法更适用于其稳定性分析。时域法中的核心是Lyapunov稳定性原理及Lyapunov-Krasovskii泛函(L-K泛函)方法；优点在于L-K泛函的构造与解析过程可以转化为凸优化问题加以有效求解，不足之处在于其不可避免地具有一定的保守性。因此，通过适当的构造与解析技巧降低L-K泛函方法的保守性成为分析广域电力系统的动态稳定性的核心问题。

基于以上分析，建立了区间变时滞电力系统模型；提出一种新的增广向量和一种新的L-K泛函构造方法。在L-K泛函的解析过程中对积分区间进行分段处理并结合Wirtinger积分不等式有效地减少了分析结果的保守性。通过经典的单机-无穷大系统进行仿真，验证了方法的有效性。

1 时滞电力系统模型

在电力系统动态稳定分析模型中，通常用三阶微分方程表示发电机的动态过程，具体表示为

(1)

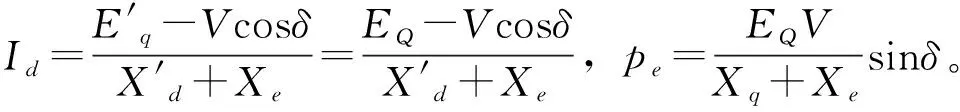
上述方程中各参数的含义见文献[8-10]。因系统中存在时滞现象，运用AVR励磁控制方式的励磁系统的动态方程可表示为

(2)

综上所述，存在时滞的电力系统状态空间模型可由式(1)和式(2)表示为

(3)

对式(3)在其平衡点处线性化可得

(4)

0≤h(t)≤h

其中，常量h>0为系统的时滞上界；常量μ1，μ2为时滞导数的上下界。

为得到本文的主要结论，需要引用以下引理。

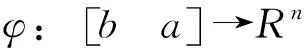
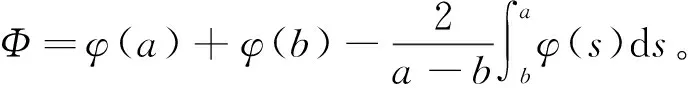
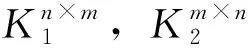
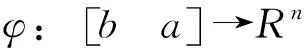
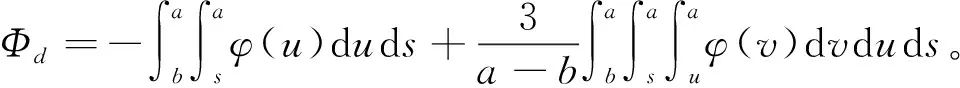
2 时变时滞电力系统稳定性分析

基于建立的广域时滞电力系统模型，通过构造新的增广向量和L-K泛函，给出了一个新的广域电力系统的稳定性结论。

首先，令：

对系统(4)构造如下L-K泛函：

(5)

其中：

P=PT>0,W=WT>0,M=MT>0,Q=QT>0,R=RT>0,Z=ZT>0,F=FT>0。

注1：与现有文献不同，这里引入新的增广向量

并且构造的泛函中包含三重积分项V5(t)，使得时滞的信息得到了充分的利用，从而降低了结论的保守性。

沿着系统(4)解轨线对V(t)求导可得

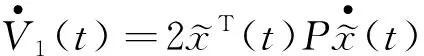
(6)

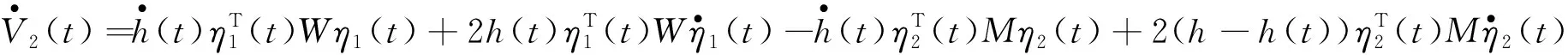
(7)

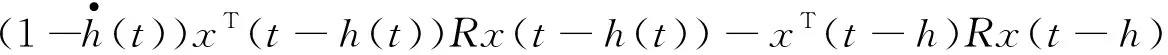
(8)

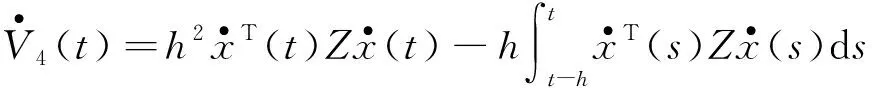
(9)

(10)

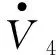
(11)

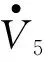
(12)

(13)

(14)

(15)

结合式(6)～式(15)得

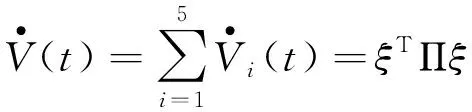
(16)

基于以上证明过程，下面给出系统(4)渐近稳定的主要结论。

定理1：给定常数h,μ1,μ2,若存在正定对称矩阵P∈R5n×5n,W∈R2n×2n,M∈R2n×2n，Q∈Rn×n,R∈Rn×n,Z∈Rn×n,F∈Rn×n,对称矩阵B∈R3n×3n,L∈R3n×3n,以及适当维数的矩阵G∈R3n×n,N∈R3n×n,C∈R3n×n,使得以下矩阵不等式成立，则系统(4)是渐近稳定的：

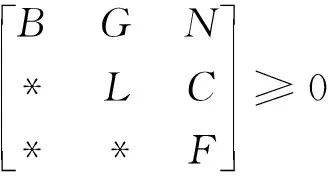
Π=[Eij]<0，(i,j=1,2,…,7)

(17)

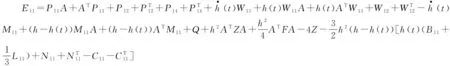
E13=-P13-M12+Y11+Y21-Y12-Y22

E15=-P15+(h-h(t))(P31A+P32+P34+M21A)+2Y12+2Y22

E23=-Y11+Y21+Y12-Y22-2Z

E33=-R-4Z

E34=-h(t)P23-2Y21+2Y22

E35=(h(t)-h)P33-M22+6Z

E36=-h(t)P43

E37=(h(t)-h)P53

E55=(h(t)-h)P35-12Z-3h2F

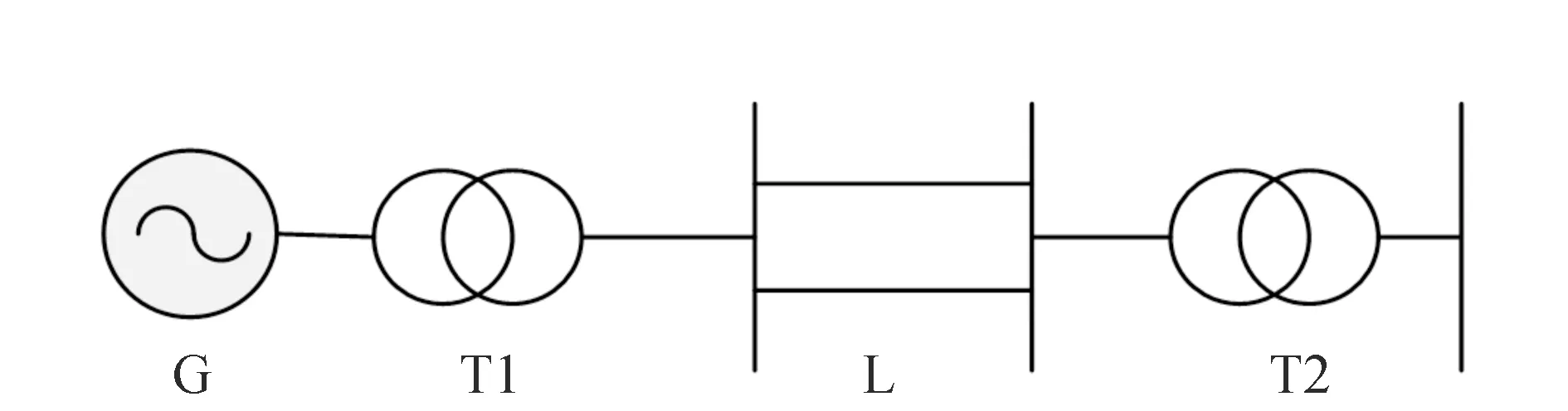
图1 单机-无穷大系统Fig.1 Single-machine infinite-bus system

3 仿真分析

通过仿真分析验证提出方法的有效性。

例1：选用单机-无穷大系统(图1)验证本文所提方法的有效性，该系统具体参数的取值见文献[14]。

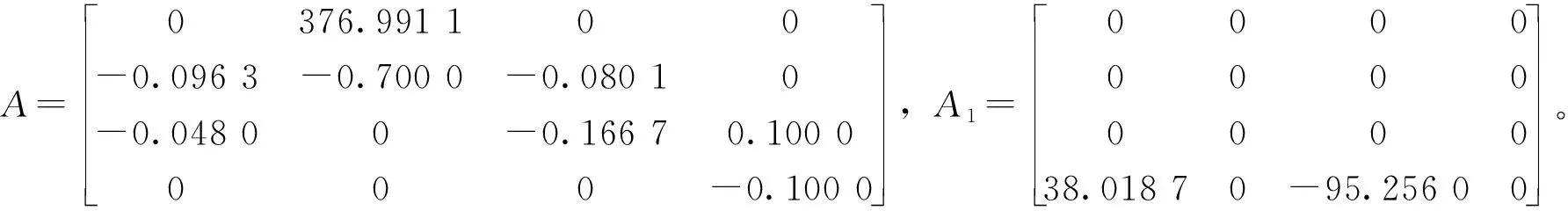
在系统无扰动时，采用不同的方法得到的单机-无穷大系统的最大稳定裕度。利用Matlab软件LMI工具箱求解得到的稳定裕度：本文方法(定理1)为71.90 ms，文献[4]为65.4 ms，文献[7]为65.4 ms，文献[8]为65.29 ms，文献[10]为61.3 ms，采用本文方法得到的稳定裕度最大，结论的保守性更小。

假设系统中存在励磁放大系数扰动：

令矩阵H,Ea,Eb分别取值为

设r∈ [0,10],分别求出当r=0.5,1,1.5,2,…,10时，采用不同方法所得最大时滞值见表1。

随着扰动项r的增大，系统的稳定裕度逐渐减小。与文献[8-9，14]相比，本文所得到稳定判据的保守性更小；换言之，系统稳定运行区域更大。

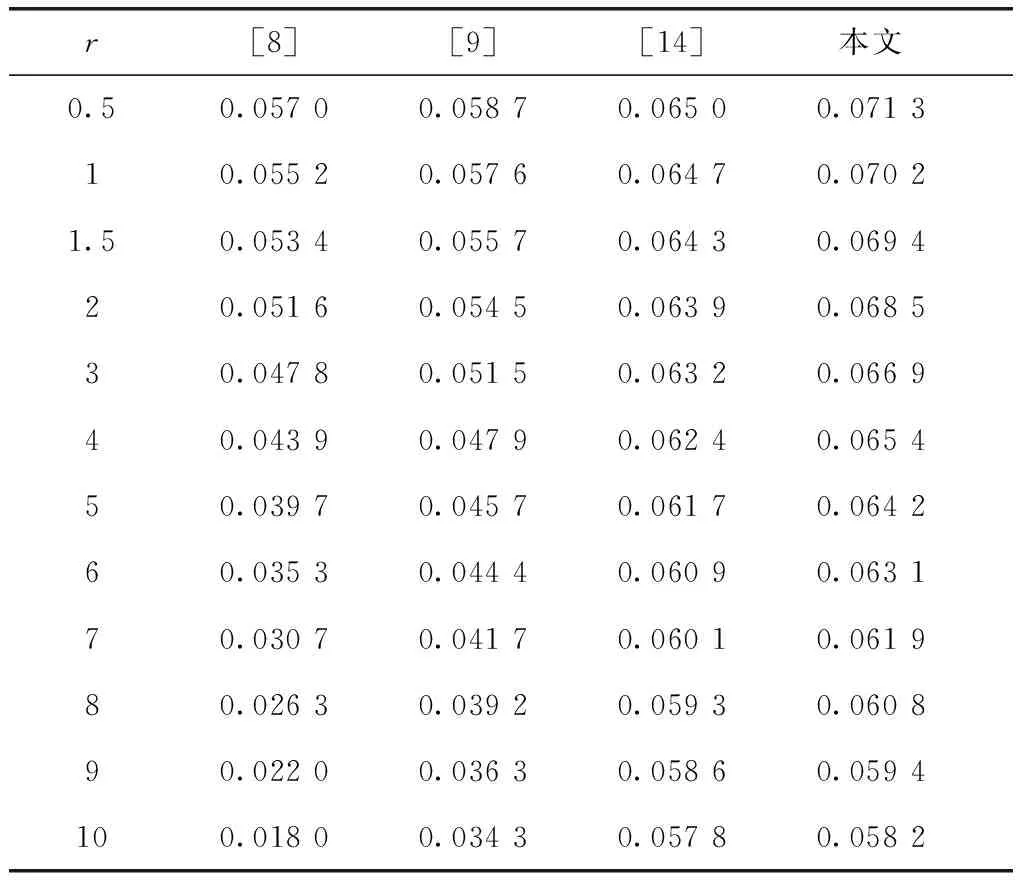
表1 不同r值求得的时滞最大值

4 结 论

考虑到时滞现象对电力系统稳定运行产生的影响，通过建立广域区间变时滞电力系统模型，利用时滞系统模型来分析电力系统的动态稳定性问题。通过构造新的L-K泛函，并在解析过程中引入时滞分割及积分不等式技巧，得到了保守性较小的稳定性判据。仿真分析说明了该方法有效地扩大了系统的稳定运行区域。