调速侧电力系统稳定器优化设计方法

林耀东

同济大学 电子与信息工程学院 上海 201804

1 设计背景

低频振荡始终是电力系统稳定性中不可忽视的问题,无论是区域间低频振荡[1],还是局部低频振荡[2],都会给系统带来极大的危害。

电力系统低频振荡通常指频率在0.2～2.5 Hz范围内的振荡[3]。为研究电力系统的低频振荡问题,一般情况下需要对电力系统进行线性化分析。Heffron等[4]提出Philips-Heffron模型,被广泛应用于电力系统的线性化分析。在Philips-Heffron模型的基础上,Demello等[5]提出同步发电机阻尼转矩和同步转矩,从力学角度对电力系统的稳定性进行了分析。此外,Demello等[5]还研究了励磁系统对电力系统阻尼转矩和同步转矩的影响,证明高增益励磁系统可能会导致电力系统阻尼转矩变负,使电力系统不稳定。当然,不只是励磁系统,调速系统同样会对电力系统的阻尼转矩产生影响。王官宏、陶向宇等[6]在Philips-Heffron模型的基础上加入调速系统模型,分析调速系统对电力系统阻尼转矩的影响,证明当调速系统对转速偏差输入造成的角度偏差为-90°～90°时,调速系统提供正阻尼,角度偏差为90°～270°时,调速系统提供负阻尼。王官宏、黄兴[7]证明调速系统放大倍数在正阻尼区间内增大会增大电力系统的正阻尼,在负阻尼区间内增大会增大电力系统的负阻尼。提升电力系统的稳定性,在本质上是增大电力系统的阻尼转矩。Demello等[5]研究发现在电压调节器输入端叠加合适的反馈信号,能够增大电力系统的阻尼转矩。以这一概念为基础设计的电力系统稳定器,对低频振荡有很好的抑制效果。与励磁系统的电力系统稳定器原理类似,调速系统也有相应的调速侧电力系统稳定器。郝玉山等[8]研究调速侧电力系统稳定器在单机无穷大系统中的应用,针对调速侧电力系统稳定器在调速系统中的叠加点、结构、基本原理进行可行性分析。Chen Yujiao等[9]基于广域测量信号对调速侧电力系统稳定器进行优化设计,其性能优于仅基于本地信号设计的调速侧电力系统稳定器。Mayouf等[10]在调速侧电力系统稳定器的设计中加入模糊逻辑控制,进一步增强对电力系统低频振荡的抑制作用。在单机无穷大系统调速侧电力系统稳定器设计理论的基础上,郝玉山等[11]将调速侧电力系统稳定器推广应用至多机系统。Mayouf等[12]应用遗传算法对采用模糊逻辑控制的多机调速侧电力系统稳定器进行优化设计。

在实际工程中,电力系统除了需要满足稳定性要求外,电力系统的调节速度还需要满足一次调频相关的标准要求。但是,在前述调速侧电力系统稳定器设计中，都以电力系统的稳定性为目标,未考虑电力系统的一次调频性能。笔者在同时考虑电力系统稳定性和一次调频性能的情况下,对调速侧电力系统稳定器进行优化设计,并通过仿真验证了设计方法的有效性。

2 调速系统对同步电机阻尼的影响

同步电机线性化模型的转子运动方程为:

(1)

式中:TJ为同步电机惯性时间常数;Δω为转速角速度增量;ΔTM为机械转矩增量;ΔTE为电磁转矩增量;D为阻尼因数;Δδ为功角增量;ω0为额定转速角速度;s为拉普拉斯变量。

假设调速系统传递函数Gg(s)为:

Gg(s)=ΔTM/-Δω

(2)

若只考虑调速系统对同步电机的影响,则同步电机的转子运动方程可改写为:

TJsΔω=-Gg(s)Δω

(3)

将s=jωd代入式(3),ωd为电力系统振荡频率,可得:

TJsΔω=-HgejφgΔω

=-Hg(cosφg+jsinφg)Δω

(4)

式中:Hg为Gg(s)的幅值;φg为Gg(s)的相角。

同样,将s=jωd代入式(1),可得:

jωdΔδ=ω0Δω

(5)

将式(5)代入式(4),可得:

TJsΔω=-HgΔωcosφg+HgΔδ(ωd/ω0)sinφg

=-DgΔω+KgΔδ

(6)

ω0=2πf0

(7)

Dg=Hgcosφg

(8)

Kg=Hg(ωd/ω0)sinφg

(9)

式中:f0为电网额定频率;Dg为调速系统附加阻尼转矩因数;Kg为调速系统附加同步转矩因数。

由式(6)可知,当-90°<φg<90°时,Dg>0,此时调速系统提供正阻尼;当90°<φg<270°时,Dg<0,此时调速系统提供负阻尼。

3 电力系统稳定性和同步电机一次调频性能

根据Q/GDW 1404—2015《国家电网安全稳定计算技术规范》[13]提出的稳定性要求,在正常方式下,电力系统中区域间振荡模式及与大机组相关的局部振荡模式在小扰动情况下的最低阻尼比ξ应不小于0.03。

除此之外,Q/GDW 669—2011《火力发电机组一次调频试验导则》[14]对火力发电机一次调频性能提出以下要求:机组参与一次调频的响应时间trd应短于3 s,机组参与一次调频的稳定时间tst应短于1 min,对于机组一次调频的负荷响应速度,燃煤机组达到75%目标负荷的时间t75应不长于15 s,达到90%目标负荷的时间t90应不长于30 s。

综上所述,电力系统应满足以下约束:

(10)

4 调速侧电力系统稳定器基本原理

由式(6)可知,调速系统附加阻尼转矩的大小与调速系统传递函数Gg(s)的相角φg有直接关系。因此,可以通过附加反控制信号改变φg,改善调速系统的阻尼特性,从而达到抑制振荡的效果。

包含调速侧电力系统稳定器的单机无穷大系统控制框图如图1所示。

加入调速侧电力系统稳定器后,式(3)需要修正为:

TJsΔω=-[1+Ggpss(s)]Gg(s)Δω

(11)

式中:Ggpss(s)为调速侧电力系统稳定器传递函数。

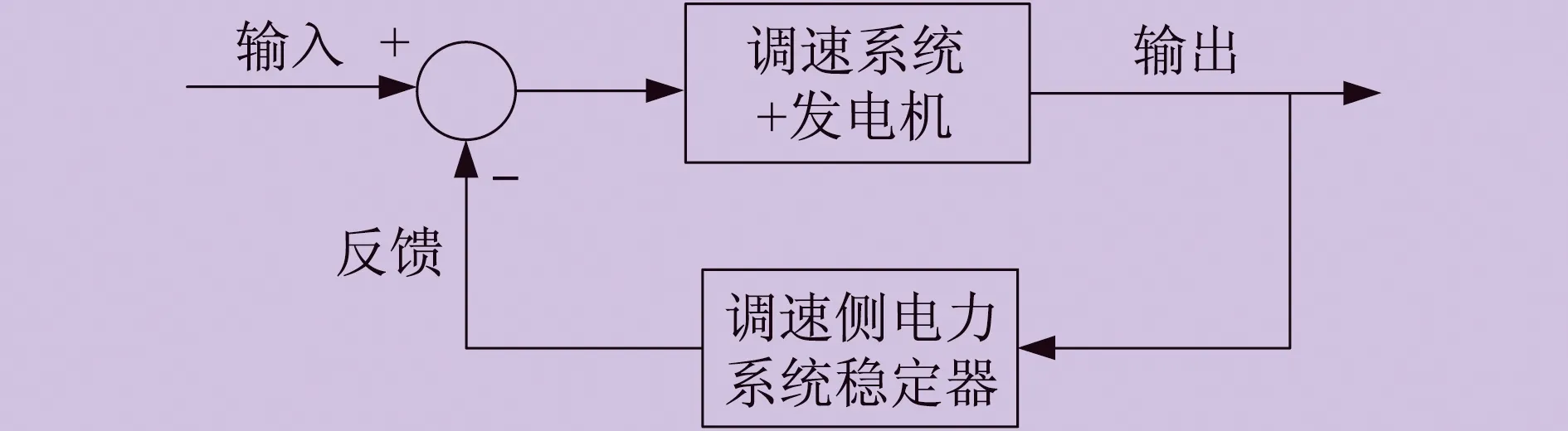
图1 单机无穷大系统控制框图

仿照式(3)～式(6)过程对式(11)进行变换,得到:

TJsΔω=-HgΔωcosφg+HgΔδ(ωd/ω0)sinφg

-HgpssHgΔωcos(φgpss+φg)

+HgpssHgΔδ(ωd/ω0)sin(φgpss+φg)

=-D′gΔω+K′gΔδ

(12)

D′g=Hgcosφg+HgpssHgcos(φgpss+φg)

(13)

K′g=Hg(ωd/ω0)sinφg+HgpssHg(ωd/ω0)

sin(φgpss+φg)

(14)

式中:Hgpss为Ggpss(s)的幅值;φgpss为Ggpss(s)的相角;D′g为修正后调速系统的附加阻尼转矩因数;K′g为修正后调速系统的附加同步转矩因数。

对比式(6)和式(12),可知调速侧电力系统稳定器的加入为同步电机提供了额外转矩增量ΔTMgpss,为:

ΔTMgpss=-HgpssHgΔωcos(φgpss+φg)

+HgpssHgΔδ(ωd/ω0)

sin(φgpss+φg)

(15)

额外的阻尼转矩增量ΔTMDgpss为:

ΔTMDgpss=-HgpssHgΔωcos(φgpss+φg)

(16)

若要调速系统提供正阻尼,D′g应大于0,则调速侧电力系统稳定器的Hgpss和φgpss应满足:

cosφg+Hgpsscos(φgpss+φg)>0

(17)

5 调速侧电力系统稳定器优化设计

调速侧电力系统稳定器的优化设计分为三步:① 滤波器设计[15],根据所需的信号和系统存在的噪声频率设计滤波器;② 调速侧电力系统稳定器相角调整,根据系统需要补偿的相角设计超前滞后环节参数;③ 调速侧电力系统稳定器增益调整,考虑系统稳定性和一次调频性能要求,选取合适的调速侧电力系统稳定器增益。

假设通过上述步骤设计得到调速侧电力系统稳定器的传递函数为:

Ggpss(s)=KgpssGfil(s)G′gpss(s)

(18)

式中:Kgpss为调速侧电力系统稳定器增益;Gfil(s)为带通滤波器传递函数;G′gpss(s)为相角补偿环节传递函数。

5.1 滤波器设计

通常情况下,调速侧电力系统稳定器以同步电机转速作为输入量。除此之外,在同步电机稳定运行的情况下,同步电机的转速等于转速给定值,此时调速侧电力系统稳定器的输出应为零。

综合以上分析,滤波器在保留低频振荡信号的同时,应具有消除直流分量和高频噪声的特性。

滤除直流分量可以通过高通滤波器实现。同时,还应保留频率在0.2 Hz以上的信号。因此,选择的高通滤波器传递函数Ghighpass(s)为:

(19)

高通滤波器传递函数伯德图如图2所示。

图2 高通滤波器传递函数伯德图

高通滤波器的截止频率约为0.053 Hz。

通过低通滤波器滤除2.5 Hz以上的噪声信号,选择的低通滤波器传递函数Glowpass(s)为:

(20)

低通滤波器传递函数伯德图如图3所示。

低通滤波器的截止频率约为3.2 Hz。

将高通滤波器与低通滤波器串联,组成带通滤波器,其传递函数Gfil(s)为:

(21)

带通滤波器传递函数伯德图如图4所示。

带通滤波器的通带为0.053～3.2 Hz。

5.2 调速侧电力系统稳定器相角调整

由式(15)可知,调速侧电力系统稳定器的加入为系统提供了额外转矩。假设调速侧电力系统稳定器只增加系统的阻尼转矩,由式(15)可知,调速侧电力系统稳定器传递函数的相角φgpss应满足:

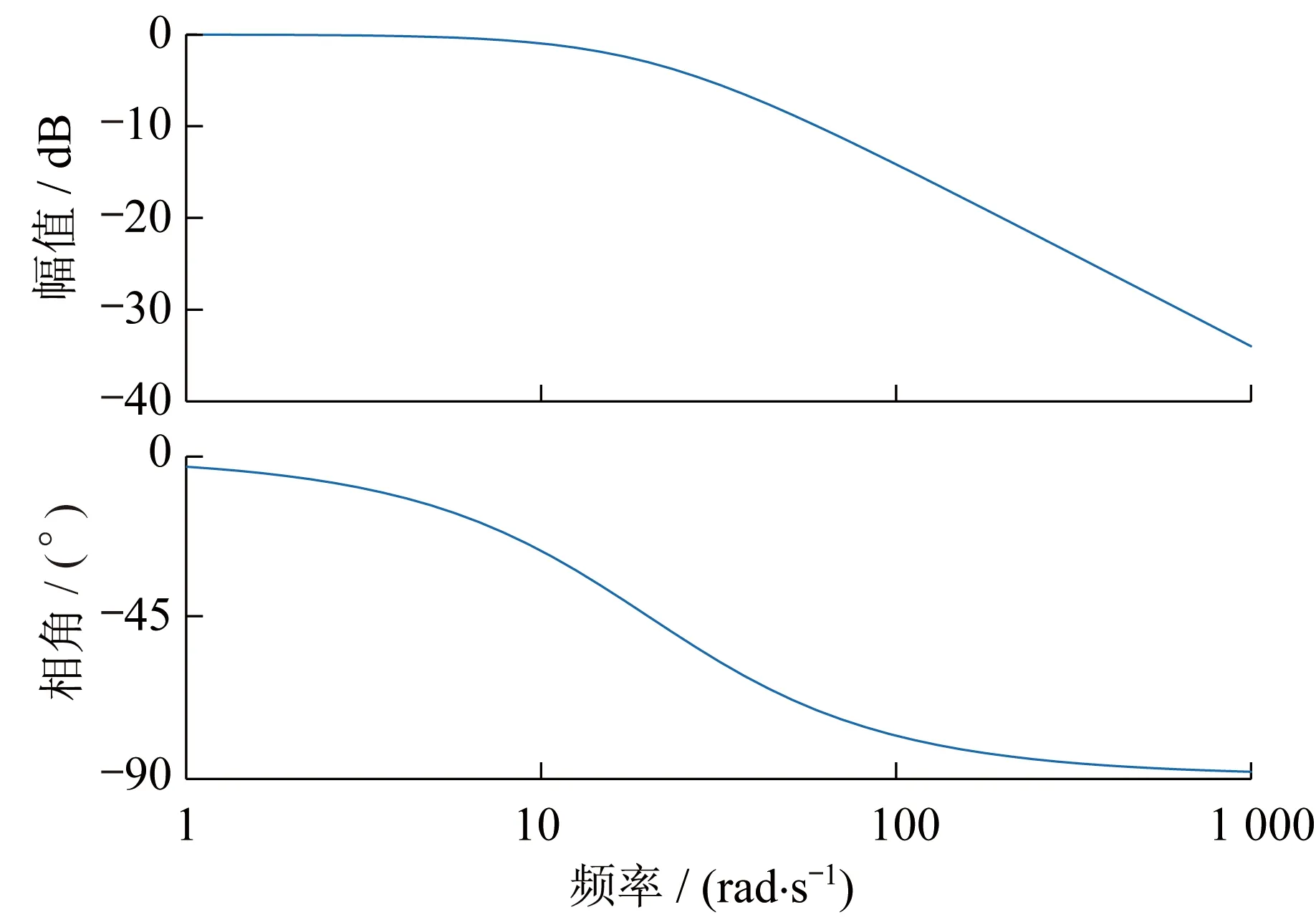
图3 低通滤波器传递函数伯德图

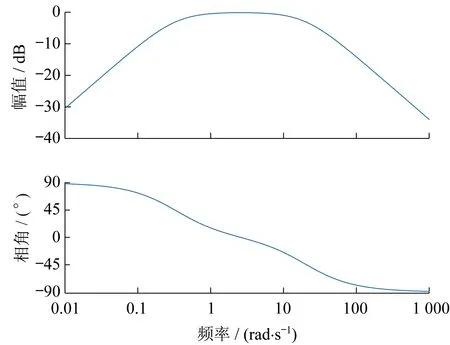
图4 带通滤波器传递函数伯德图

φgpss+φg=0

(22)

即:

φgpss=-φg

(23)

φgpss中包含滤波器造成的相角变化φfil和超前滞后环节造成的相角变化φ′gpss。超前滞后环节造成的相角变化φ′gpss为:

φ′gpss=-φg-φfil

(24)

对于n阶超前滞后环节,传递函数G′gpss(s)为:

(25)

式中:T为调速侧电力系统稳定器时间常数;α为调速侧电力系统稳定器时间比例常数。

每个环节需要补偿的相角θ为:

θ=φ′gpss/n

(26)

求解式(25)中的参数α和T,得:

(27)

(28)

将求解参数代入式(25),得到完整的调速侧电力系统稳定器超前滞后环节传递函数。

5.3 调速侧电力系统稳定器增益调整

由式(16)、式(18)可知,调速侧电力系统稳定器的增益Kgpss直接决定调速侧电力系统稳定器提供阻尼的大小。若Kgpss取值偏大,有可能导致系统一次调频性能下降或其它模式增幅振荡产生。若Kgpss取值偏小,则无法有效抑制低频振荡。在同时考虑系统稳定性和一次调频性能要求的情况下,Kgpss需要满足相应的约束条件:

(29)

式中:Kmin1、Kmin2、Kmin3、Kmin4、Kmin5为各约束条件对应的Kgpss取值范围下限;Kmax1、Kmax2、Kmax3、Kmax4、Kmax5为各约束条件对应的Kgpss取值范围上限。

取交集,将式(29)合并,得到Kgpss的取值范围为:

(30)

6 算例

笔者以某电厂发电机为例,搭建单机无穷大系统仿真模型,验证调速侧电力系统稳定器优化设计方法的有效性。

滤波器设计已详细介绍,滤波器的传递函数为式(21)。

计算补偿相角及补偿环节参数。系统特征值见表1。

系统存在频率为1.351 Hz的负阻尼振荡模式。需要配置调速侧电力系统稳定器的调速系统模型如图5所示。图5中,Pcv为调门指令,Pgv为调门开度。

s=jωd=j2π×1.351=j8.49

将s代入式(3)、式(4)、式(21),计算得到:

φg=210.3°

φfil=-20.8°

90°<φg<270°,调速系统提供负阻尼。

将φg、φfil代入式(24),得到需要补偿的相角φ′gpss为:

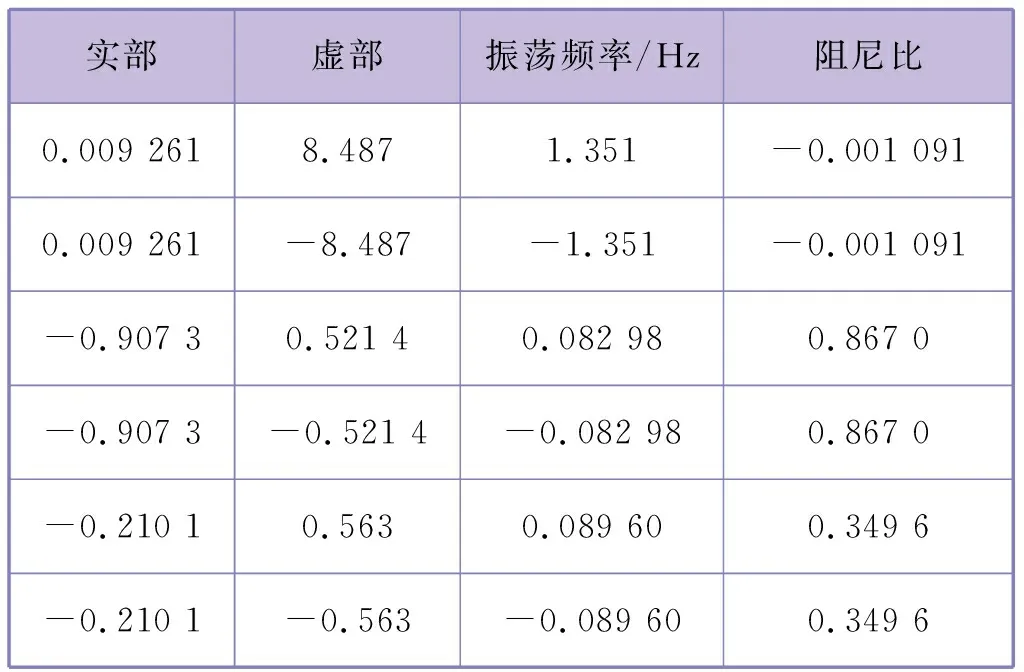
表1 系统特征值

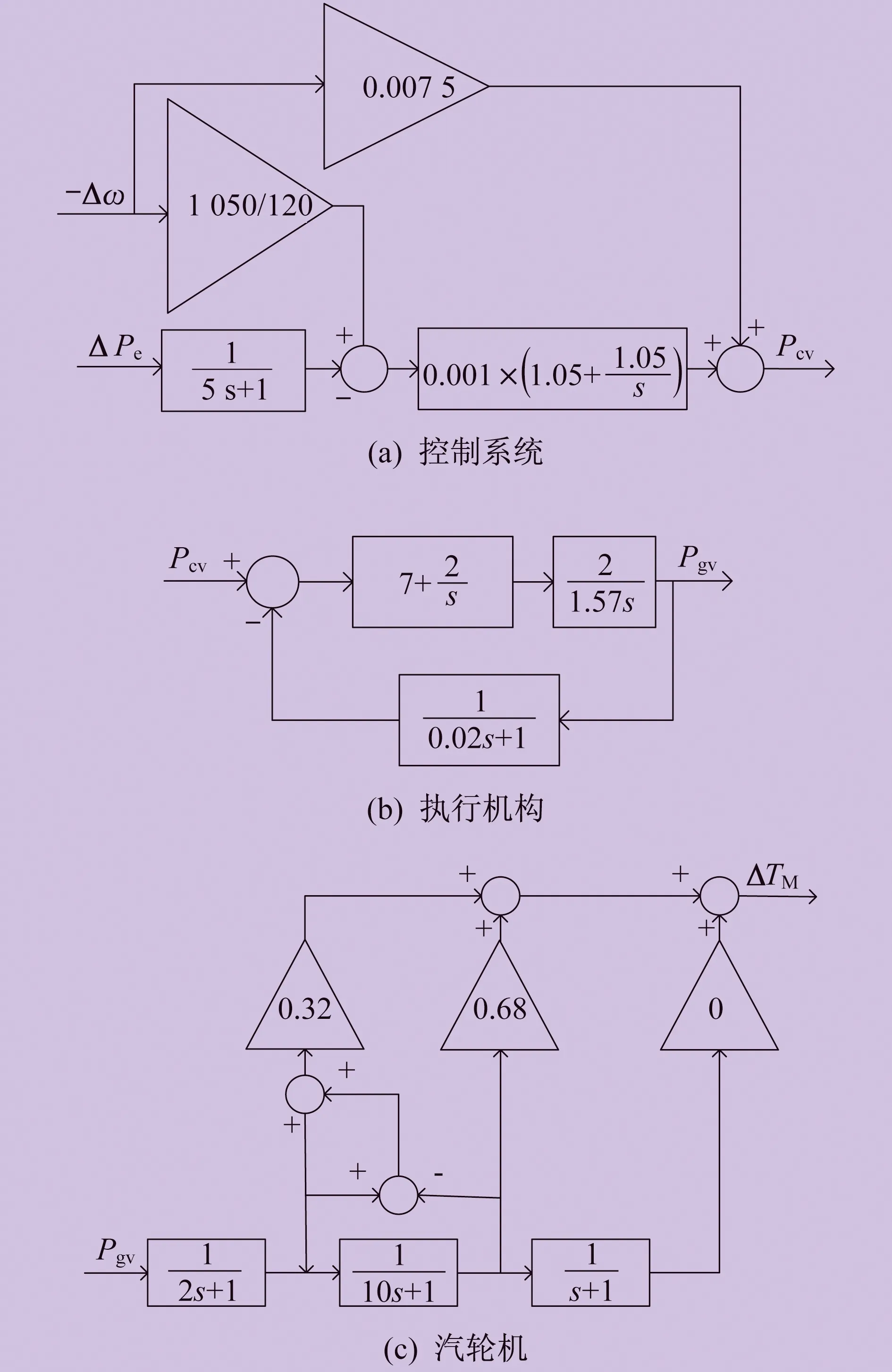
图5 调速系统模型

φ′gpss=-(210.3°-360°)+20.8°=170.5°

选用三阶超前滞后环节进行补偿,每个环节需补偿的相角θ为:

θ=170.5°/3=56.8°

计算式(25)的参数,得:

由系统根轨迹图得,在满足电力系统稳定性要求的情况下,Kgpss应满足:

0.023

(31)

最后,考虑电力系统一次调频性能要求对Kgpss的约束。通过仿真试验的方法,在式(31)的基础上确定满足一次调频性能的Kgpss取值范围。

发电机一次调频性能试验电磁功率偏差标幺值仿真曲线如图6所示。由图6可知,在满足式(31)的情况下,电力系统满足一次调频性能要求。

图6 发电机一次调频性能试验电磁功率偏差标幺值仿真曲线

因此,同时满足电力系统稳定性和一次调频性能要求的Kgpss取值范围为式(31)。

7 结束语

笔者对调速系统削弱电力系统阻尼的原理进行了分析。在此基础上,提出调速侧电力系统稳定器的优化设计方法,在满足电力系统稳定性要求的同时还满足电力系统一次调频性能要求。具体优化设计过程为:设计带通滤波器,使调速侧电力系统稳定器只保留低频振荡信号;设计相角补偿环节,使调速侧电力系统稳定器为电力系统提供正阻尼转矩;选取合适的调速侧电力系统稳定器增益,使调速侧电力系统稳定器同时满足电力系统稳定性和一次调频性能要求。最后通过仿真验证了优化设计方法的有效性。