理工科大学生创新能力影响因素的评估分析

疏瑞文

（安徽理工大学 化学工程学院,安徽 淮南232001）

0 引言

高校学生是我国从事科技创新事业的一支重要力量，然而影响其创新能力的因素目前不够明确。因此，研究影响大学生创新能力的各种内在和外在因素，找出主要因素，对大学生创新能力的培养和提升具有重要意义[1-2]。由于专业背景的特殊性和面向工程应用的就业岗位，对于理工科大学生来说，创新能力的培养与提升极为重要[3]。由于影响大学生创新能力因素的复杂性和多变性，因此难以对其进行定性和定量评估。层次分析法（AHP）是一种处理复杂问题的理想方法[4]，其通过综合分析影响大学生创新的各种因素，借助专家经验和量化处理，有望揭示影响其创新能力的主要因素[5-6]。

1 建立大学生创新能力评估指标体系

研究发现，外部环境和自身因素是影响大学生创新能力的两个主要方面[7]。针对理工科大学生创新能力的影响因素，本文从社会因素、导师因素、平台建设、考核机制、个人因素等5个方面建立一级指标，并进一步分解为20个二级指标[8]。其中个人因素是评价大学生创新能力的主要指标，它反映了大学生所具备的创新能力，具体指标体系详见图1。

图1 AHP模型的指标体系

2 层次分析法的分析过程

AHP的基本思路：将一个多目标的复杂问题分解成数个彼此关联、层次递阶的系统结构，该结构可清楚地反映出目标、对象、准则等因素之间的关联，从而可以进行判断、比较，最后筛选出最优的方案[9]。具体步骤如下：

2.1 构建层次结构模型

利用AHP处理实际问题时，首先依据问题的性质和实现的目标，将其分解成若干组成因素；其次根据各组成因素之间的关系由上至下形成不同的层次，上一层对下一层有着支配作用[10]。通常只有一个最高层，即目标层，是问题分析中预设定的目标；中间层也叫准则层，是由一个或几个层构成，主要为目标实现的中间环节；最底层是方案层，是目标实现所提供的各种方案、决策、措施或具体指标等。

2.2 构造判断矩阵

上下层之间关系的确定是基于递阶层次结构来建立的[10]。通过分析这些具体的元素，按照上一层的相对重要性，给对应的因素赋予相应的权重。AHP中通常采用的是两两比较法，重要性程度的比较一般采用“1-9”标度法[10]，如表1所示。运用判断矩阵的方法来计算，具体方法是对方案中各个备选方案采用两两比较的方法，确定两者之间相互重要的程度。得出判断矩阵A=（aij）n*n。

公式（1）中aij为因素i与因素j重要性的比较结果。判断矩阵A有以下3个特征：

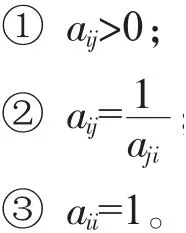
表1 重要性程度比较表

2.3 计算权重

将A按列进行归一化处理得到[11-12]：

将每列元素正规化，并按行相加获得[11-12]：

将得到的和向量正规化得到[11-12]：

得到的wi，即为所求的权重向量。

2.4 一致性检验

计算最大特征根λmax[12]：

计算一致性指标CI[12]：

得到平均随机一致性指标RI如表2所示：

表2 判断矩阵平均随机一致性指标

计算一致性比例CR[12]：

当CR≥0.1时，表明权重分配不合理，则需要构建新的判断矩阵；反之，当CR＜0.1时，判断矩阵符合一致性，因此权重分配是合理的。

2.5 层次总排序

层次总排序即为计算某一层全部因素对最高层影响的权重值，通常是由高层到低层排列，如表3所示。

表3 权重合成法

假定B层中B1B2……Bm对A层中因素Aj（j=1,2……m）的层次排序一致性指标为CIj，RIj是随机一致性指标，则层次总排序的一致性比例CR如公式（8）所示[12]：

通常，当CR＜0.1时，表明层次总排序满足一致性检验；反之则重新调整判断矩阵的取值中一致性比率高的，直到CR＜0.1为止，再依据这个权重做出最佳决策。

3 实例分析

本文通过对影响国内某大学理工科大学生创新能力的因素进行实例分析，建立一级和二级指标判断矩阵，计算得到各级指标所占权重，揭示影响其创新能力的主要因素。

设B1为考核机制，C1为奖励机制，C2为考核制度，C3为经费资助情况，C4为硬件资源；B2为导师因素，C5为创新指导能力，C6为导师参与积极性，C7为社会资源，C8为社会经历；B3为社会因素，C9为家庭支持程度，C10为企业参与程度，C11为就业市场认可度，C12为成功认识；B4为个人因素，C13为兴趣爱好，C14创新意志品质，C15为合作交流意识，C16为创新思维；B5为平台建设，C17为各类竞赛平台，C18为科技社会平台，C19为教学创新平台，C20为创新实验基地，利用专家评分法来确定矩阵的各项数据。根据“1-9”标度法的赋值原则得出表4。

表4 一级指标判断矩阵

表5 ～表9为二级指标对于一级指标的权重计算，结果分别如表5～表9所示：

表5 二级指标对考核机制的判断矩阵

表6 二级指标对导师因素的判断矩阵

表7 二级指标对社会因素的判断矩阵

表8 二级指标对个人因素的判断矩阵

表9 二级指标对平台建设的判断矩阵

表10 为层次分析法的各指标及权重分布。由表可知，考核机制、导师因素、社会因素、个人因素、平台建设等一级指标所占的权重分别是0.061 2、0.061 2、0.163 8、0.374 0、0.339 9。

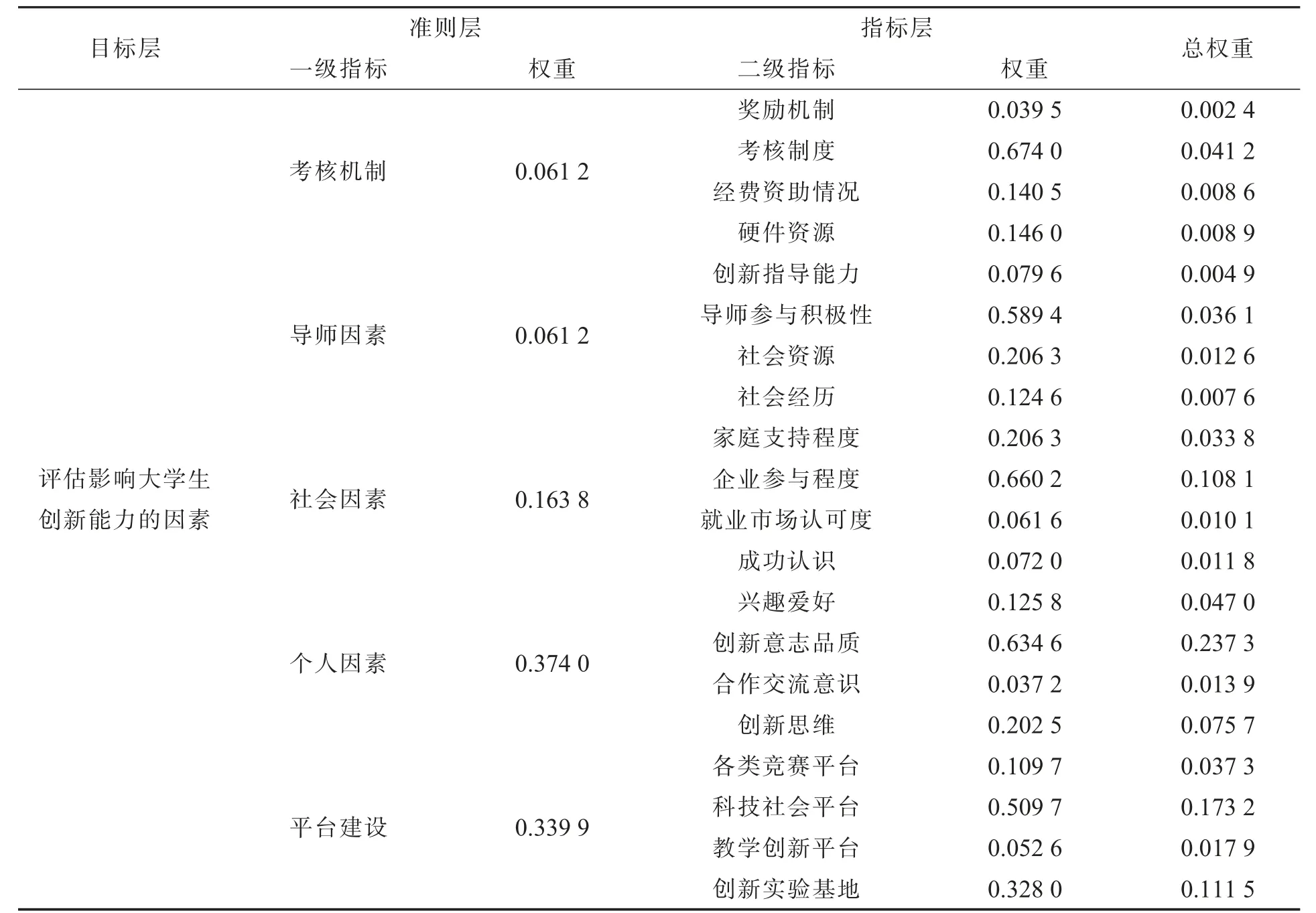
表10 层次分析法各指标及权重分布

图2 是一级指标因素权重分布图，从中可以明显看出个人因素、平台建设所占权重排在前两位，属于主要因素。

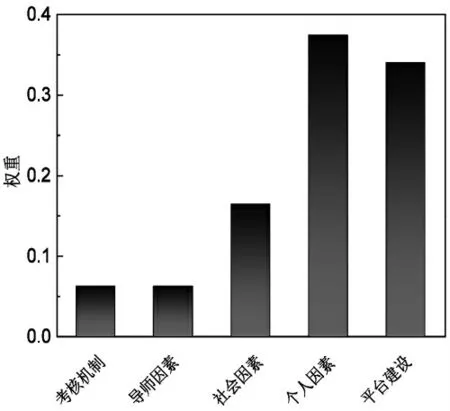
图2 一级指标因素权重分布图

图3 为二级指标因素权重分布图，由图可以发现考核制度、企业参与程度、创新意志品质、导师参与积极性、科技社会平台所占权重位列前五，属于主要二级指标。

图3 二级指标因素权重分布图

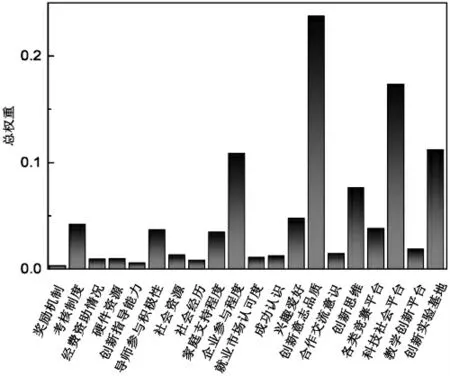
图4 总权重排序分布图

图4 为总权重排序的分布图。由图可以发现，创新意志品质、科技社会平台、创新实验基地、企业参与程度的权重分别是0.237 3、0.173 2、0.111 5、0.108 1，因此属于影响大学生创新能力的主要因素。

4 结语

采用层次分析法，建立影响理工科大学生创新能力的评估模型及一级和二级指标体系；通过实例分析影响大学生创新能力的因素，揭示影响其创新能力的一级指标、二级指标和总权重排序。结果表明：一级指标中考核机制、导师因素、社会因素、个人因素、平台建设所占的权重分别是0.061 2、0.061 2、0.163 8、0.374 0、0.339 9，个人因素和平台建设属于主要因素；二级指标中考核制度、企业参与程度、创新意志品质、导师参与积极性、科技社会平台所占权重分别为0.674 0、0.660 2、0.634 6、0.589 4、0.509 7，属于主要二级指标；总权重排序分布发现创新意志品质、科技社会平台、创新实验基地、企业参与程度是决定其创新能力的主要因素。因此，本研究有望为我国理工科大学生创新能力的培养和提升提供参考价值。