基于Inception卷积神经网络的城市快速路行程速度短时预测
2021-04-01唐克双陈思曲曹喻旻张锋鑫
唐克双,陈思曲,曹喻旻,张锋鑫
(1.同济大学道路与交通工程教育部重点实验室,上海201804;2.连云港杰瑞电子有限公司智能交通事业部,江苏连云港222061)
近年来,伴随城市化进程的加速推进和经济社会的高速发展,我国机动车保有量和驾驶人数量持续增加,城市交通拥堵问题日益严重。根据高德地图发布的《2019中国主要城市交通分析报告》,2019年全国360个主要城市高峰时段总体处于拥堵和缓行状态的比例超过60%[1]。快速路作为城市道路网络的主骨架,承担大量的通勤和过境交通需求,其拓扑结构复杂且交通拥堵,具有频率高、范围广、模式多等特点。因此,快速路对于城市道路网络整体运行效率具有重要的影响,也是交通拥堵治理的主要对象。行程速度是我国绝大部分城市计算交通指数和判别交通状态时采用的核心指标。短时行程速度可以反映实时交通运行状态,帮助交通管理者及时采取管控措施以缓解交通拥堵,并为出行者路径选择提供参考。因此,准确可靠的短时行程速度预测对于提高城市交通主动管控能力和出行信息服务质量,具有重要的意义。
目前,交通状态预测模型基本上可以分为两大类:统计学模型和神经网络模型[2]。经典的统计学模型包括历史平均模型[3]、差分整合移动平均自回归模型(autoregressive integrated moving average model,ARIMA)[4-5]和卡尔曼滤波模型[6]等。上述模型算法较为简单,适用于数据量充足且数据扰动较小的场景,但是模型的泛化能力较差,针对随机性强、平稳性差的短时交通流预测任务效果不理想[3](短时预测通常指预测时间步长小于30 min的情况)。为了增强模型对于不同类型数据的适用性,一些非参数统计学模型被逐渐应用于交通状态预测领域,例 如K-最 邻 近 算 法(K-nearest neighbor,KNN)[7]、支 持 向 量 机(support vector machine,SVM)[8]、支持向量回归(support vector regression,SVR)[9]等。非参数模型在处理动态、非线性以及具有时空关联特征的交通状态预测任务上,相对于传统的时间序列统计学模型具有一定的优势,而且可以在模型中融合环境气象等其他关联因素。但是,该类浅层结构的非参数模型对于高维交通数据和复杂交通模式的时空特征提取能力仍显不足[10]。
神经网络模型支持高维输入数据,优势在于可提取多维非线性特征,从而获得更高的模型预测精度与鲁棒性[11]。多层前馈神经网络(multilayer feedforward neural networks,MFNN)基于浅层神经网络结构,可以学习数据中的非线性关联特征,虽然其预测精度优于上述统计学模型[12-13],但是仅能提取交通数据中基本的关联特征。为进一步探究更深层、更复杂的交通流时空关联特征和演化规律,近年来深度神经网络开始被逐渐应用于交通流预测领域。深度置信网络(deep belief networks,DBN)[14-15]、堆栈自编码器(stacked auto encoder,SAE)[16]和生成式对抗网络(generative adversarial network,GAN)[17-18]作为代表性的无监督深度学习模型,以及循环神经网络(recurrent neural networks,RNN)[19-21]、图 网 络(graph neural networks,GNN)[22-23]等在交通流预测方面均取得了较好的效果。其中,DBN适用于小规模交通网络预测问题,无法充分提取多路段之间的关联性以及交通状态的长期特征[24];SAE与GAN是一类无监督的神经网络,模型通常表示为编码-解码结构,通过对输入数据特征的重构学习提高鲁棒性与精度[25];RNN在交通数据的时间序列特征学习上具有一定的优势[26],为进一步提高模型提取输入交通状态参数间依赖关系的能力,并避免传统RNN在训练过程中所产生的梯度爆炸问题,长短期记忆网络(long short-term memory,LSTM)[19-21]等结构改善的RNN模型也被应用于交通流预测。GNN中的图注意力网络(graph attention network,GAN)可结合道路拓扑结构以及交通状态时间、空间上的权重关系进行分析,在近两年得到越来越多的研究。同时,也有学者对上述模型进行组合,研究混合模型在该领域的适应性[27]。
卷积神经网络(convolutional neural networks,CNN)可通过局部连接、权值共享与下采样等方法,尽可能保留重要的参数,舍去大量非关键参数,在图像识别任务上具有优势。因此,近年来CNN被广泛应用于图像识别、目标检测等领域[28],包括交通领域的路面病害识别[29]和车辆检测[30]等。在交通状态预测方面,Ma等[31]将交通状态转为灰度图像,首次利用CNN模型预测短时行程速度。Zang等[32]提出采用图像的不同通道对参数进行表示,对交通流量、速度和占有率同时进行预测,其中速度预测误差为3 km·h-1。之后,Zang等[33]又提出基于非对称卷积核的CNN模型,通过设置不同的重要性来体现交通数据的时空特征差异,模型的平均相对误差为10%。上述研究将交通网络和交通状态构成的高维数组作为输入,CNN可以有效地提取数据中的关联特征。然而,CNN模型的缺点是无法充分考虑交通状态的时序关联特征。因此,部分学者基于CNN构建了混合CNN模型以提升预测性能。其中,将适用于处理时序数据的RNN与CNN结合是研究的一大热点,例如,采用门控循环单元(gated recurrent unit,GRU)或LSTM来增强模型的时序特征提取能力[34-35]。此外,部分混合CNN模型的研究中考虑了无监督网络、GNN的融合。Ge等[36]基于图卷积网络(graph convolutional networks,GCN)建立模型提取交通时空特征,并考虑天气、工作日等相关社会因素提高速度预测的精确性。Yu等[37]将GCN与编码-解码结构相结合建立深度学习模型进行实时预测,模型平均绝对百分比误差为7.3%。
上述混合CNN模型虽然可以通过同时考虑交通状态的时间序列特征和空间关联特征,提升传统CNN模型的预测性能,但是在CNN模型的计算部分依然采用固定的卷积核尺寸,大大限制了其对多尺度(交通拥堵的时间和空间范围动态变化)交通流特征的学习能力。此外,为提取多粒度条件下的特征,通常需要对输入数据进行集计与调整并构建多个子网络。考虑到高峰时段城市快速路的交通状态不仅受到路网拓扑结构和地面道路交通状态的影响,而且受到驾驶员动态路径选择行为和突发交通事件的影响,因此城市快速路交通拥堵模式复杂且拥堵的时空粒度范围多变。针对这样的预测任务,上述混合CNN模型存在一定局限性。
因此,本研究提出一种更加有效并能适应城市快速路复杂交通拥堵模式的行程速度短时预测模型——Inception-CNN模型。Inception-CNN模型将多粒度特征提取问题结合至模型中而非依赖于输入数据,使其更具有高效性、适应性,并更易于应用在如流量、占有率等其他交通流参数的预测任务中。其中,Inception模块是GoogleNet在2014年的ImageNet挑战赛中获胜的核心模块[38]。目前,已有学者将Inception模块引入交通领域的部分研究方向,如交通标志检测与汽车试验场外物入侵识别等[39-40]。它将CNN中的卷积核分解为更小的卷积核或非对称卷积核,并通过不同的串行与并行组合实现了高效的多尺度特征提取。该模块的加入不仅加速了网络训练过程,同时也增强了网络的特征表达能力[38]。
本研究以上海市高架快速路为研究对象,首先将线圈采集的行程速度数据组织为时空二维矩阵,并采用阈值法将数据矩阵转化为图像,以发挥CNN模型在图像识别上的优势;同时,在CNN的网络结构设计中融入Inception模块,构建了一种新的混合CNN模型框架,并通过系统的训练和测试,确定了最优结构参数和超参数。目前基于图像学习的交通流预测模型,大多仍采用传统的评价指标进行分析。为了更加科学准确地定义Inception-CNN模型对行程速度时间序列特征和时空演化特征的捕捉能力,本研究还引入了梯度幅度相似性偏差(gradient magnitude similarity deviation,GMSD)[41]指标,结合图形可视化的方法,系统、可靠地对比分析了Inception-CNN模型与ARIMA模型、浅层神经网络模型、CNN模型和RNN模型的预测性能。
1 研究地点和数据描述
1.1 研究对象
本研究以2011年全年上海市延安高架快速路的线圈检测器数据为数据源。研究范围包括延安高架快速路从四川中路到外环沪青平公路之间的路段,全长约14.3 km,含2个立体交叉以及14个上下匝道,如图1所示。研究路段沿主线布设35个检测断面(断面编号为0~34),分车道共113个线圈检测器(主线为3车道,部分上下匝道处车道数变化)。原始线圈数据的采样间隔为20 s,包括流量、速度和时间占有率三个参数。在本研究中,基于行程速度的短时预测时间步长的考虑,将原始车道级线圈数据根据流量加权平均集计成为5 min间隔的断面级检测数据。同时,由于凌晨0点至5点半常为维修时段,存在大量数据缺失的现象,故在本研究进行了删除。针对剩余数据中的异常值,部分采用基于时间序列的线性插值修复,即采用前后时段或相邻周同一天的数据进行处理;另一部分则基于相邻线圈检测器数据从空间维度进行修复,即采用经过时间推演的前后断面数据。经处理后的行程速度分布均值为61.77 km·h-1,标 准 差 为16.58 km·h-1,偏 度为-0.92。

图1 研究路段区位Fig.1 Location of the studied site
1.2 行程速度时空图像生成方法
本研究首先将原始线圈检测数据处理为行程速度时空图像,作为模型的输入。以x轴为时间段,y轴为检测器布设段,得到行程速度时空矩阵S的表达式如下:式中:n为时间段总数;m为检测断面总数;vm,n为检测器断面m在第n个时间段的行程速度,km·h-1。未进行数据预处理前,本研究的时间段总数n为288,检测断面总数m为35。基于行程速度时空矩阵,通过一定的映射方法可得到能反映交通状态时空变化特征的行程速度时空图像,见图2。其中,颜色的映射标准参照上海市交通状态指数划分标准[42]。

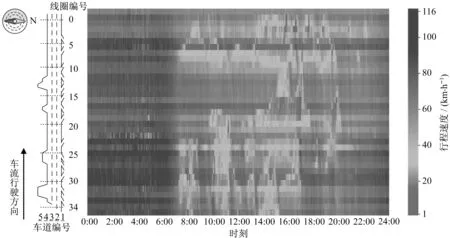
图2 行程速度时空图像Fig.2 Time-space travelling speed image
2 模型构建及训练
2.1 CNN模型基本原理
CNN主要由卷积层、池化层与全连接层组成,卷积层可有效提取目标特征,同时具有稀疏连接、参数共享的特点,其计算原理如下:
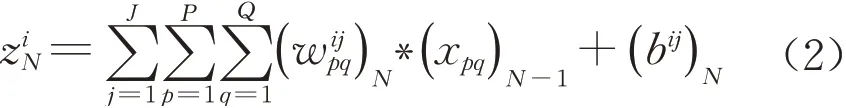
式中:N为所在网络层的位置;ziN为位于N位置卷积层的第i个卷积值;wijpq为卷积核i第j通道在(p,q)位置处的参数值;xpq为当前卷积核或池化算子在滑动计算时视野范围内在(p,q)位置处的上一网络层输入值;bij为偏置系数。卷积层所输出的特征图是基于卷积结果,通过非线性激活函数的变换所得:

式中:g(x)为非线性激活函数;y为输出的特征图。本研究选取Sigmoid、tanh与ReLU(rectified linear unit)三种不同的激活函数进行模型的对比分析与结构优化[43]。池化层对输入的特征图进行下采样操作,可在减少模型待训练参数数量的同时提高所提取与识别特征的泛化能力,以最大池化为例:
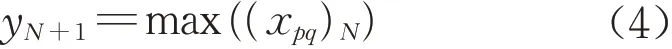
式中:max(x)为求最大元素值函数。最后将特征图展平为一维张量,并连接若干全连接层,输出预测结果,其基本结构见图3。图中,例如,“卷积层6,28×28”表示得到6张特征图,其中每张特征图像素大小为28×28。本研究在训练时以平均绝对误差(mean absolute error,MAE)为目标函数,即fMAE;同时结合平均绝对百分比误差(mean absolute percentage error,MAPE)指标,即fMAPE,对模型结果进行评价分析。

式中:u为真实值;û为预测值;n为样本量。
2.2 Inception-CNN模型
在基本的CNN中,为提取不同粒度的特征,通常需要输入对应尺寸(规模)的图像(行程速度时空图像),即不易直接有效学习不同规模的交通时空特征。此外,在设计基本CNN模型的卷积、池化算子的尺寸时,大多通过实验者较为主观地确定最佳搜索范围,并通过网格搜索或是随机搜索方式来确定最优的选择。考虑到交通演变规律的不确定性,即交通事件或交通拥堵影响范围的不确定性,在CNN的每个卷积层或池化层中采用一致的算子尺寸并非合适。因此,本研究将基于CNN,结合Inception模块建立更适应于城市快速路行程速度短时预测的深度学习模型(Inception-CNN模型)以解决上述问题。
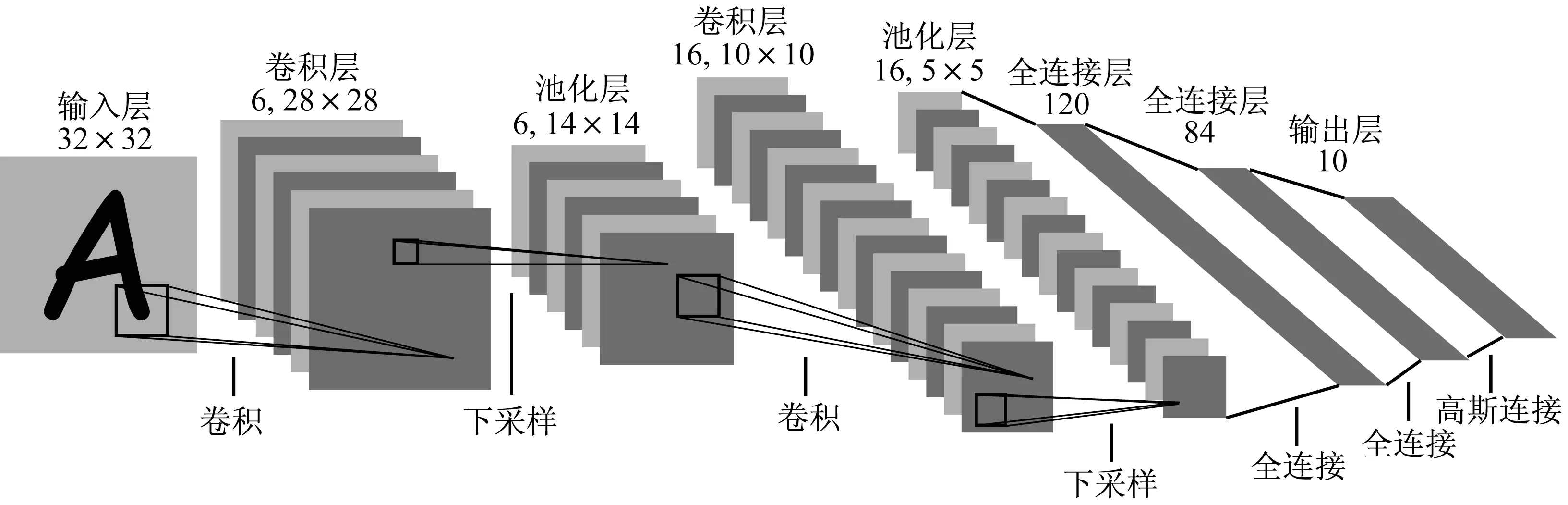
图3 卷积神经网络结构(LeNet-5[44])Fig.3 Structure of CNN(LeNet-5)
Inception模块可将卷积核分解为尺寸更小的对称或非对称的卷积核,并通过一系列串行或并行的组合,保持每个模块输出特征图的尺寸一致。例如,图4展示了5×5像素范围内的卷积核由2个3×3的卷积核串行组合替代的过程,同时3×3的卷积核还可由1个1×3与1个3×1的非对称卷积核串行组合替代。此外,在Inception-CNN模型中,还可将池化算子与卷积进行混合,并行组合各项操作,如图4所示。

图4 将5×5卷积核替换为2个3×3卷积核的Inception模块[38]Fig.4 Inception modules where each 5×5 convolution is replaced by two 3×3 convolution
通过结合Inception模块,本研究搭建的模型可更准确地提取交通数据不同尺度的时序特征、空间特征以及时空特征。如图5所示,行程速度时空图像的横轴表示空间关联,纵轴表示时间关联,以此表征交通状态。那么,连续两次q×q的卷积则可作为2q-1粒度下的时空特征提取器;连续的1×p、p×1卷积则是经过非线性增强的p粒度下的空间、时序特征提取器;而先进行r×r池化再进行o×o卷积的过程则可作为r+o-1粒度下更加鲁棒的关联特征。特征图的拼接操作对不同通道的信息进行组合,增强不同粒度特征间的交互性。在一个Inception模块中,可以串行或并行组合各种不同尺寸的卷积与池化算子,以提高模型非线性特征的表达能力,即进一步学习交通数据的高维时间、空间与时空关联特征。同时,非对称卷积核的加入也使得模型能以不同的重要性提取不同场景下的时间或空间维度特征。
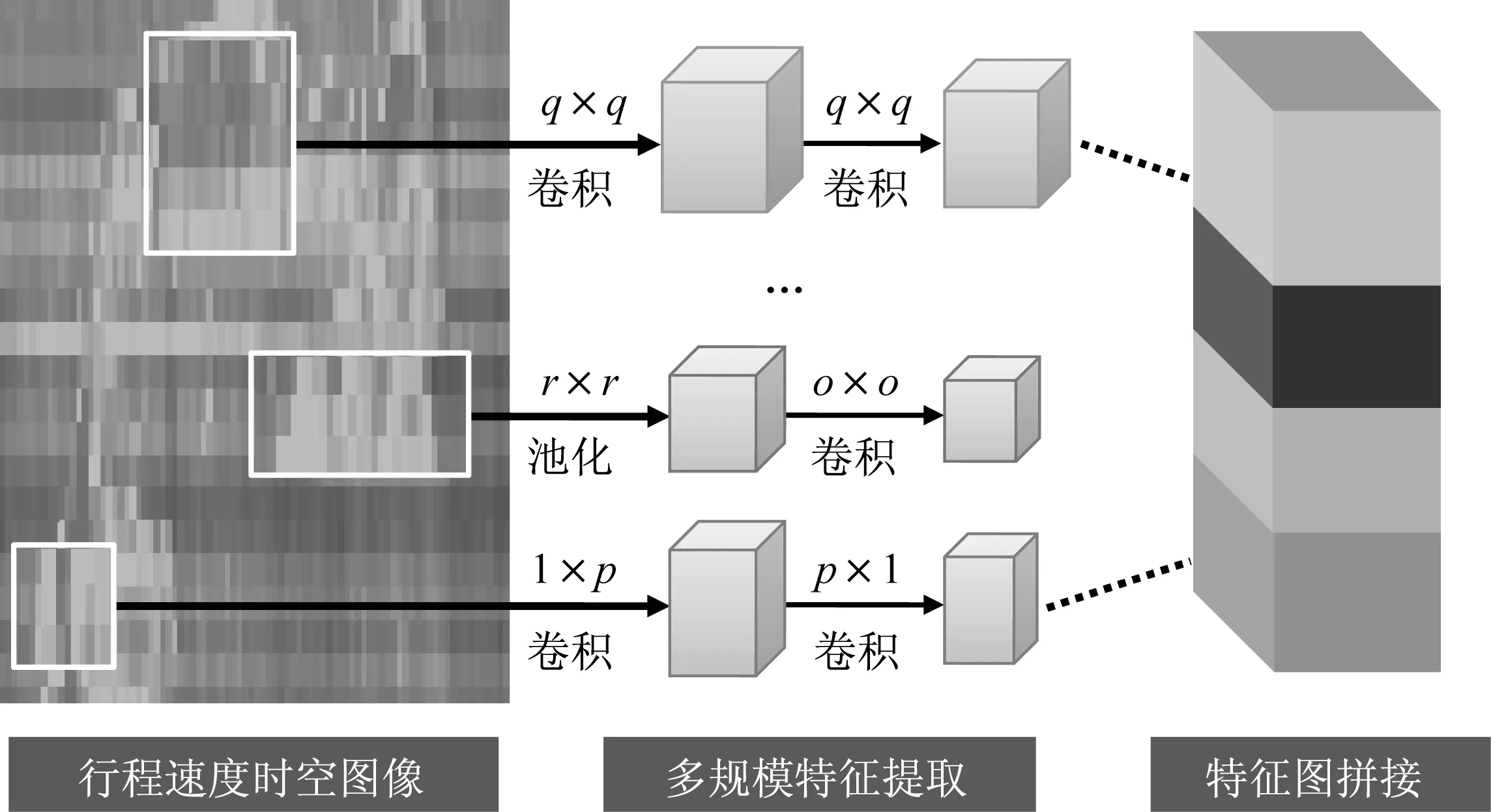
图5 Inception-CNN模型中的卷积核设计及其计算过程Fig.5 Design and computing process of convolutional kernels in Inception-CNN
总结而言,Inception-CNN模型对城市快速路的行程速度短时预测问题具有较好的适应性,其基本结构见图6。由于单层的Inception模块已具有较强的非线性表达能力,故本研究仅考虑单层或双层的Inception模块组合,使得模型更加轻量化并避免过拟合现象。

图6 Inception-CNN模型基本结构Fig.6 Basic structure of Inception-CNN
2.3 模型设计与优化思路
在本研究中,首先设计模型的结构参数,如神经网络层数,各层神经元数量等。其次,对模型的优化参数进行比选,包括:初始学习率与学习率变动计划、批处理大小、激活函数以及各类算子的尺寸与步长等。不同结构参数与优化参数的组合见表1。
其中,数据集的大小为75 300组,选自上海市2011年349 d的延安高架快速路的线圈检测器数据。以训练集、验证集、测试集的比例为0.8:0.1:0.1划分数据集,即约选取60 300组作为训练集,7 500组作为验证集,7 500组作为测试集对模型进行训练。
2.4 模型训练结果
本研究工作环境是内存为16 GB,GPU为Tesla P100的服务器,采用Tensorflow深度学习框架。所得到的最优Inception-CNN示意图见图7(基于输入时间步长为30 min,下同),共包含831.3万个待训练权值参数,训练时长为771 s。图中,CONV1~CONV12表 示 卷 积 层,Avgpool 1~Avgpool2表示平均池化层,Maxpool1表示最大池化层,FC1~FC2表示全连接层,Y为预测结果。
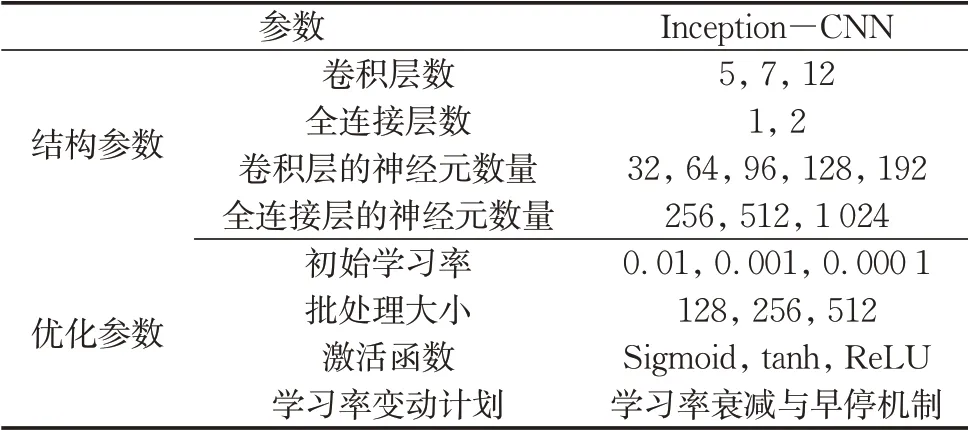
表1 结构结构参数与优化参数Tab.1 Structural parameters and optimization parameters
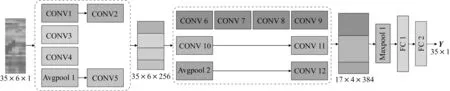
图7 最优Inception-CNN结构Fig.7 Optimum structure of Inception-CNN
模型参数信息见表2,输入的图像大小为35×6×1,其中35代表35个断面,6代表6个时间步长,1代表单通道。通过实验,批处理大小设置为256,激活函数为ReLU,初始学习率为0.001。在第一个Inception模块中,共包含4种卷积或池化算子的组合:2个卷积层,分别有64个大小为3×3的卷积核;1个卷积层,包含96个大小为3×3的卷积核;1个卷积层,包含64个大小为1×1的卷积核;1个卷积层与1个池化层,分别有64个大小为1×1的卷积核与大小为3×3的平均池化算子。在第二个Inception模块中,共包含3种卷积或池化算子的组合:4个卷积层,分别有128个大小为1×3与3×1的卷积核;2个卷积层,分别有192个大小为1×3与3×1的卷积核;1个卷积层与1个池化层,分别有大小为2×2的平均池化算子与64个大小为3×3的卷积核。综上,Inception-CNN模型所学习得到的交通状态时空关联特征将具有复杂性、多样性。

表2 Inception-CNN模型参数信息Tab.2 Parameter configuration of Inception-CNN
3 模型评价
本研究选取了经典的统计学模型与浅层、深层神经网络对模型结果进行综合评价,包括不同输入时间步长下模型的稳定性,模型精度,以及模型时序、时空特征学习能力的分析。涉及的模型有:针对时间序列问题应用广泛的数理统计学模型ARIMA;一定深度的人工神经网络(artificial neural network,ANN),具有3个隐藏层,各层神经元数量分别为512、512、256,共包含51.1万个待训练参数;对于序列数据有较好适应性的神经网络RNN,具有2个隐藏层(LSTM结构),各层神经元数量均为128,共包含135.7万个待训练参数;以及不包含Inception模块的基本CNN,具有两个卷积层、池化层与全连接层,各层神经元数量分别为:256、512、1 024、512,共包含1 011.5万个待训练参数。其中,各神经网络结构见图8。

图8 对比模型结构Fig.8 Architecture of comparison model
3.1 预测稳定性与精度评价
由于输入时间步长会影响到模型的预测精度与预测结果的稳定性[31]。故,首先根据2.3中设定的30、45、60 min不同的输入时间步长进行模型对比分析,各个神经网络模型以不同的初始值与不同的训练集划分方式(随机选取)进行训练,记录多次训练中预测结果的平均值与方差,见图9。其中,填充区域表示标准差。可以得到,当输入30 min历史数据时,各个神经网络模型的预测MAE与多次训练中的标准差均最低。即,在该场景下,模型的预测表现与预测结果稳定性均较优。说明交通状态的演变具有时效性,30 min的历史数据中包含了足够的有效特征,当输入数据的时间跨度继续增大时,将引入无效的信息。故下文的对比分析都基于该场景。
模型预测精度分析结果如表3所示。Inception-CNN模型预测误差最小,较传统数理统计模型下降了31.37%,其预测精度也有1.83%的提升。ARIMA模型由于进行单点预测,耗时远高于其他模型;ANN、RNN、CNN模型的训练时间花费分别为75、1 660以及343 s,结合模型待训练参数数量进行考量,Inception-CNN模型的训练效率仅略次于CNN模型。
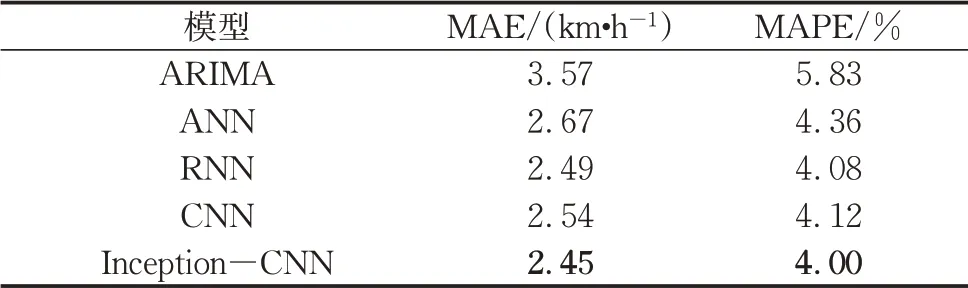
表3模型预测MAE与MAPETab.3 MAEs and MAPEs of the model predictions
为进一步分析模型的精度,本文将数据集划分为工作日、非工作日以及所有时间三类。在此基础上,对模型进行训练并取得最优结构,结果见图10。分析发现,在三个场景下,模型预测得到的MAE值具有相同的的变化趋势:(1)非工作日<所有时间<工作日;(2)Inception-CNN<RNN<CNN<ANN<ARIMA。其中,第一个结论是由于非工作日的交通事件较少,而工作日的常发性与偶发性交通事件都有所上升,增加了预测任务的难度。从第二个结论以及图9可以看出,Inception-CNN可对不同场景下多尺度复杂的交通模式进行更为有效的特征提取,在交通拥堵常发性与偶发性特性表现不一致的工作日与非工作日,以及包含不同程度信息量的不同输入时间步长条件下均有较好的预测精度。

图10 不同数据集下模型结果Fig.10 Model results in different dataset
3.2 时序特征学习能力评价
由于交通数据具有较强的时序特征,故本小节对各个模型在该方面的提取能力进行分析。首先利用线性回归方法计算模型对每个线圈的预测值与真实值之间的差异,随后对35个线圈的计算值进行平均,见表4。其中,k为斜率,b为y轴上的截距,R2为线性回归决定系数。可以看出,Inception-CNN模型的回归效果最优,R2为0.920 3。此结论反映出Inception-CNN模型对于时序特征的学习能力较强,甚至优于对于时序数据有较强适应性的RNN模型,其原因可能在于Inception-CNN中存在多个尺度不一的交通状态时序特征提取器,同时混合多维度特征的分析预测也有利于单维度特征提取任务。

表4 模型回归分析结果Tab.4 Regression analysis of models
为进一步说明上述结论,选取2011年1月3日的数据进行可视化展示,见图11。ANN模型的行程速度预测时变曲线与真实曲线的相近程度优于ARIMA模型;ARIMA模型的预测曲线有波动异常的现象,同时与真实曲线存在着变化趋势相反或延迟的区段。而深度神经网络模型,如RNN、CNN以及本文提出的Inception-CNN模型的预测结果均较好,可选取早高峰时段再进行细部比较。
根据图12,可以看出,RNN与CNN模型均具备反映行程速度时变基本特征与趋势的能力;而Inception-CNN模型在此基础上,可得到与真实行程速度距离更小的时变曲线。即在时序特征学习方面,Inception-CNN模型可通过提取不同粒度下的关联性,准确预测每个线圈(断面)时段内的速度变化趋势与大小。

图11 行程速度预测时变曲线Fig.11 Time-varying curve of travelling speed prediction
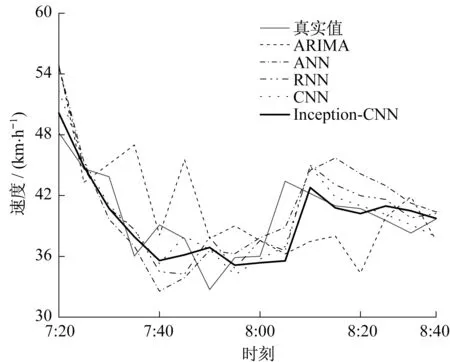
图12 行程速度预测时变曲线(早高峰时段)Fig.12 Time-varying curve of travelling speed prediction(morning rush hour)
3.3 时空特征学习能力评价
根据图2可以看出,行程速度时空图像通过描绘交通事件的轮廓表征交通状态的演变过程,其中不同颜色交界的边缘(交通事件的影响范围)框定了不同的交通状态,是交通管理与控制中较为重要的组成部分。本研究为进一步得到模型时空特征学习能力,将会从图像分析的角度对行程速度预测结果再深入分析。而传统的误差检测方法,如MAE与MAPE指标并无法有效地对其评估,故本研究引入了一种图像质量的评估方法对真实图像与预测图像的差异进行分析。该方法借助的指标为GMSD,可借助梯度幅值反映结构信息,基于局部质量退化在图像全局上的变化反映图像的质量,对图像边缘特征的变化较为敏感。本研究中选择的卷积算子为Prewitt算子[41],利用上述算子对图像进行卷积操作,即可得到图像在水平与垂直方向上的梯度幅值,进而计算图像的各个局部梯度场rGMS(i),最后求得梯度场的偏差GMSD值rGMSD,其计算公式如下:

式(7)计算结果如图13所示。

图13模型GMSD计算结果Fig.13 GMSD of models
行程速度时空图像与计算GMSD过程中得到的卷积特征图如图14所示,包含真实值与Inception-CNN模型预测值。其中,GMSD的计算值越低,代表预测图像与真实图像之间的一致性越强。根据图13与图14可以得到,ARIMA的GMSD最高,该模型预测所得的行程速度时空图像可能存在一定的噪声;由ANN至RNN至CNN,模型生成的图像质量逐渐提升;而Inception-CNN模型所得到的行程速度时空图像与真实图像的一致性最强,GMSD达到0.126 8,远低于其他模型。较低的GMSD指标说明基于Inception-CNN模型预测结果生成的行程速度时空图像可以更加准确地描述各个交通拥堵的时间与空间边缘(交通状态产生较大变化),即在准确定位交通拥堵时空位置的基础上,能较为清晰有效地体现交通拥堵发生、延续和消散的动态过程。故Inception-CNN模型可通过串行或并行组合尺寸不一的卷积及池化算子,对行程速度时空图像中影响范围、持续时间、严重程度不同的多粒度的交通事件(不同颜色框定的区域)进行较为准确的识别与特征提取,进而充分学习交通状态的时空特征。同时还可得到,相较于表3,在图13中Inception-CNN模型的性能远胜于其他模型,即GMSD指标对于评估基于图像的交通流预测方法有更好的适用性,可提供更具参考价值的结果。
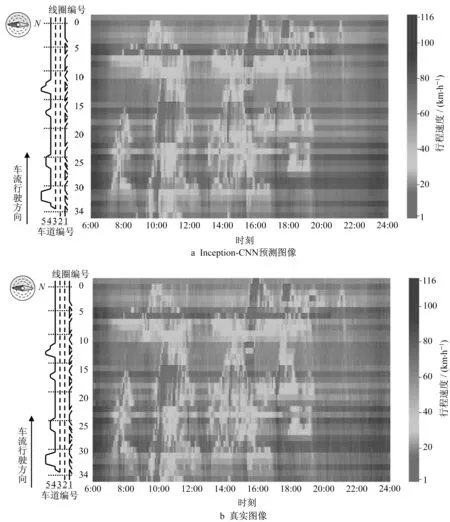
图14 行程速度时空图像对比Fig.14 Comparison of time-space travelling speed images
4 结论
(1)提出了一种新的针对城市快速路行程速度短时预测的混合CNN模型——Inception-CNN模型。该模型以交通数据生成的行程速度时空图像为特征学习对象,自动学习复杂交通拥堵模式及其演化特征,对时空等高维关联性进行多粒度特征提取,行程速度预测误差仅为2.45 km·h-1,预测精度超过95%。
(2)针对基于图像学习的交通流预测方法,引入了GMSD指标并结合回归分析方法定量评价了模型学习交通流时间序列特征和时空关联特征的能力,弥补了传统评价指标的不足,丰富了该类模型在交通流预测方面的评价方法。结果表明,Inception-CNN模型能有效提取交通数据的时间序列和时空关联特征,预测结果所生成的行程速度时空图像可准确反映交通拥堵在时空层面产生、延续、消散的过程。
(3)对比分析了不同输入时间步长和预测场景下的模型预测性能。此外,本研究针对行程速度短时预测任务所建立的Inception-CNN模型和指标评价体系可应用于其他交通参数如流量、占有率的短时预测任务与定量结果分析中。
(4)本研究的数据源单一且研究范围有限,后续研究可进一步结合交通事件和气象检测数据,并将研究范围扩大至拓扑结构更复杂的区域城市快速路网,以测试本研究所提出的Inception-CNN模型的有效性。
作者贡献申明:
唐克双:提出研究思路、撰写和修改文稿;
陈思曲:处理实证数据、构建模型算法、撰写文稿;
曹喻旻:设计模型实验、修改文稿;
张锋鑫:提出模型框架、分析实验结果、修改文稿。
