基于生态模型模拟结果的一种统计分析方法
2021-04-01郭玉珊
董 莹, 金 玥, 郭玉珊
(1.大连民族大学 a.理学院; b. 信息与通信工程学院, 辽宁 大连 116605;. 上海啊克瀚餐饮管理有限公司 市场部,上海 200010)
植被净第一性生产力(NPP)作为生态系统功能的重要指标,既可以反映植被的生长状况,又是生物圈内碳循环的重要分量[1]。而研究草地植被净第一性生产力的方法也是多种多样的,最容易想到的办法就是直接测量,也就是所说的站点实测法,使用这种方法虽然很简单,但会耗费大量的人力物力,浪费时间,调查的范围很小,完全不利于对于大范围全球尺度上数据的收集。基于这些弊端,人类想出了通过建立数学模型来估算草地植被净第一性生产力。目前这种方法已经广泛应用在调查检验中。
建立数学模型的方法来计算草地植被净第一性生产力也会产生许多问题,其中最突出的就是关于模拟数据的准确性,模型所模拟出的结果与实测值是否存在着巨大的差异。气候的变化也影响植被的生长[2],为此就需要对模型模拟值与实测值进行统计分析。进而判断出哪种模型更加合理,才能更多地被使用和推广,或者对某些模型进行改进。
气候生产力模型的估算中,Miami模型和ThornthwaiteMemorial模型模拟的草地植被净第一性生产力及分布比较相似[3]。所以本文主要就这两种草地植被净第一性生产力统计模型——Miami模型和ThornthwaiteMemorial模型的模拟值与实测值的结果进行变量的显著性检验以及拟合优度检验,从而判断哪种模型更适合中国草地植被净第一性生产力的研究,与中国实际情况更相符。
1 生物模型
1.1 Miami模型
1972年Lieth在Miami的一个学术研讨会上提出这个模型[4]。Miami模型是第一个用环境变量估算全球植被净第一性生产力的数学模型,为植被净第一性生产力的计算探索出了一条新路。Miami模型属于统计模型,变量个数较少,操作比较简单[3]。Miami模型选择了两个常用的气候指标来使用:一个是年平均温度t(℃),另一个是年平均降水量r(mm),利用全世界53个植被净第一性生产力的样本数据,利用最小二乘法建立了植被净第一性生产力与两个变量之间的定量表达式为
(1)
NPPr=3000(1-e-0.000654r)。
(2)
在实际使用中,根据Liebig最小因子定律,选择数值较低的一个作为最终结果。Miami模型考虑了与陆地生物生长以及分布密切关系的因素——温度和有效水分,并且模型的参数容易获得,在使用上具有简单快捷的优势[5]。
1.2 Thornthwaite Memorial模型
基于Thornthwaite发展的可能蒸散量模型和与Miami模型相同的世界五大洲的植被净第一性生产力实测资料,Lieth等人提出了ThornthwaiteMemorial模型[6]:
NPP=3000(1-e-0.0009695|E-20|),
(3)
(4)
式中:E为年实际蒸散量,mm;L为该地年最大蒸散量,mm;t为年均温度,℃;r为年降水量,mm。
ThornthwaiteMemorial模型本身具有生物学基础,不只是一个普通的气候动力学方程,而是植被净第一性生产力的函数形式,有利于了解温度湿度的变化对草地生产潜力影响的情况[5]。
2 回归分析
2.1 绘制散点图判断线性关系
在进行一元线性回归统计分析时,首先通过绘制散点图来判断变量之间的关系形态,散点图可以通过各种统计软件得到,本文主要使用R语言来进行辅助;若是线性关系,就可以利用相关系数来测量两个变量之间的关系强度,进而对相关系数进行显著性检验,来判断样本反映的关系是否代表两个变量总体上的关系[7-9]。
在线性相关中,两个变量的变动方向一致,称为正相关;如果方向不一致,称为负相关。散点图虽然可以判断两个变量之间有没有相关关系,并对关系形态有大体上的描绘,但是散点图并不能准确地反映变量之间的关系强度。因此,为了衡量两个变量之间的关系强弱,需要计算相关系数,记作r,公式为
(5)
如果0 本文所涉及的只有一个自变量,因此所使用的是一元线性回归方程进行分析。根据两个气候相关统计模型可以对观察值与两个模型的模拟值建立两个一元线性回归直线方程分别为 y1=α1+β1x, (6) y2=α2+β2x。 (7) (8) (9) (10) 通过使用R语言软件分别得出两种模型估计的一元回归线性方程及其散点图。散点图如图1和图2[10]。 两种模型估计的一元回归线性方程为 (11) (12) 图1 公式(11)散点图 图2 公式(12)散点图 (13) (14) (15) 式中:MSE表示的是均方残差;Sy1y1是公式(8)中关于y的总校正平方和;Sx1y1是公式(8)中观察值xy的校正交叉乘积和,表示为: (16) (17) 查t分布表可以得到t10,0.05(双侧)=2.228,对公式(8)、 (9)来说,它们的t值均小于2.228,说明两种模型的模拟值在统计学意义上与观察值不存在明显区别,即两种模型均可以准确的模拟观察值。因此需要进一步进行讨论,观察回归直线的拟合优度。 由于上一小节对回归系数的检验并没有得到明确的结论说明那个模型的模拟程度较好,因此需要对两条回归直线继续进行分析。本节所用到的检验方法就是拟合优度检验。 拟合优度检验的目的是建立度量被解释变量的变动在多大程度上能够被所估计的回归方程所揭示的指标,直观的想法是比较估计值与实际值,即使用y围绕其均值的变异的平方和,作为需要通过回归来解释其变动的度量;拟合优度检验是对样本回归直线与样本观测值之间拟合程度的检验,度量拟合优度的指标为判定系数R2[14]。 (18) 式中:SSR表示的是回归平方和;SST表示的是总平方和。R2越接近1,说明实测值与模拟值之间的关系越相近,拟合优度越好。 (19) (20) 现实情况中,所测量的许多数据会存在误差或者模型一开始的系数不是根据中国生态环境大数据计算所得出的,因此模型的本身就存在着一定的误差。所以应根据中国的生态环境和各种自然环境因素,建立更多以中国生态因素为基础的模型才能更准确的估算中国植被的净第一性生产力。2.2 建立一元线性回归方程


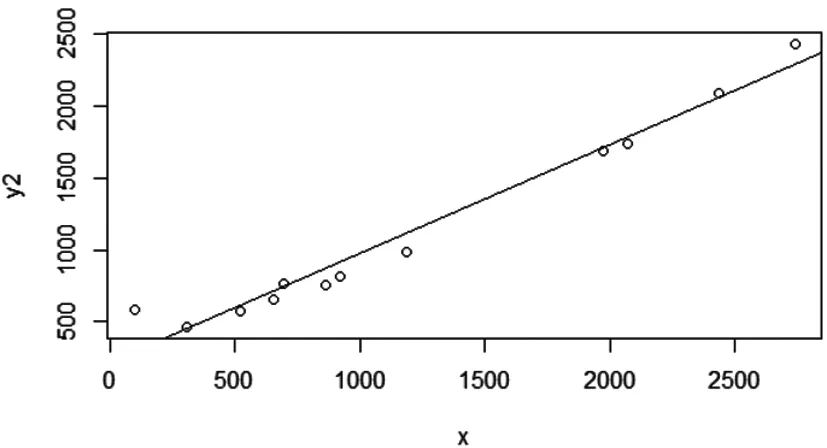

2.3 回归系数的检验


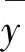
2.4 回归直线的拟合优度
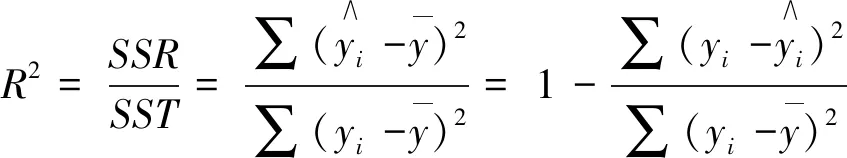
3 结 语
