基于混杂切换方法的离散切换系统状态反馈H∞控制
2021-04-01李娇,刘满
李 娇,刘 满
(大连民族大学 理学院,辽宁 大连 116605)
切换系统作为一类特殊的混杂系统,为很多具有切换特征的物理系统的研究提供方法和技术上的借鉴和启示。在过去的十几年里,人们已经对切换系统进行了研究[1-5]。然而,由于连续和离散动态相互作用,导致切换系统呈现出复杂的动态行为[6-8],因此,对切换系统的研究比较困难,仍有一些问题待解决。
稳定性分析、控制器和切换律设计是切换系统研究的主要问题[9-10]。针对连续切换系统的稳定性和镇定问题,当所有子系统稳定或部分子系统稳定或所有子系统均不稳定的情形,已得到一些相应的研究结果。例如,当每个子系统都稳定,文献[11]和[12]讨论了时间依赖切换技术。文献[13]和[14]和文献[15]分别将这些结果推广到部分子系统不稳定和所有子系统均不稳定的情形。此外,文献[13]讨论了l2增益问题。
文献[16]和[17]研究了离散时间的型式,文献[18]和[19]将其扩展到异步切换的情况。另一方面,文献[20]讨论了状态依赖切换方法。在文献[21]中,利用Lyapunov-Metzler不等式分别给出了连续和离散切换系统的稳定性条件,虽然这些条件不要求每个系统的稳定性,但子系统矩阵乘以某些常数是稳定的。此外,文献[22]依据修改的Lyapunov-Metzler不等式得到了稳定性分析和控制设计条件。显然,上述那些方法不能保证连续切换之间的任何最小驻留时间。文献[9]设计了一个具有时间约束的状态依赖切换律,保证了连续切换系统的稳定性。然而,现有的大多数连续切换系统的方法和结果不能直接推广到离散形式。因此,如何为离散切换系统设计一个具有驻留时间约束的状态依赖切换律以实现控制目标是一个复杂且困难的问题。受文献[9]启发,可看作是文献[9]的平行结果。
鉴于以上考虑,本文的目的是为离散切换系统设计一个具有驻留时间约束的状态依赖切换律。在所有子系统均不稳定的情形下,设计的切换律和子系统控制器保证了切换系统的稳定性和l2增益性能。本文主要贡献如下:(1)设计的切换律具有慢切换和快切换的优势。(2) 不要求每个子系统稳定,也不要求子系统矩阵乘以某些常数是稳定的。(3)本文结果是现有结果关于状态依赖切换或时间依赖切换的扩展。
1 问题描述
考虑如下离散切换线性系统:
x(t+1)=Aσ(t)x(t)+B1,σ(t)ω(t)+B2,σ(t)u(t),x(0)=0;
z(t)=C1,σ(t)x(t)+D11,σ(t)ω(t)+D12,σ(t)u(t)。
(1)
式中:t=1,2,…;x∈Rn是系统状态;u∈Rp是控制输入;ω∈Rq是属于l2的外部扰动及z∈Rr是受控输出。切换律σ(t)∈{1,2,…,N}∘Ai,B1,i,B2,i,C1,i,D11,i,D12,i(i∈1,2,…,N)是适当维数的常值矩阵。假设切换系统(1)满足一个最小驻留时间约束τh+1-τh≥T,T≥2, ∀h=1,2,…,τ1,τ2,…是切换时刻。
本文的控制目标是同时设计具有驻留时间约束的状态依赖切换律和子系统控制器,得到保证系统(1)(ω=0)渐进稳定且具有l2增益性能的充分条件。
2 切换稳定性
针对每个子系统均不稳定,设计一个混杂切换律仍能保证切换系统(1)(ω=0,u=0)的稳定性。
首先给出一个在后面的定理中将用到的引理。
引理1[9,23]对于t∈[t0,tf]和tf-t0=δ, 有两个对称矩阵P1>0和P2>0, 使得
(2)
(3)
成立,则系统x(t+1)=Ax(t)的Lyapunov 函数V(t)=x′(t)P(t)x(t)。

(4)
基于引理1可以得到下面的结果:
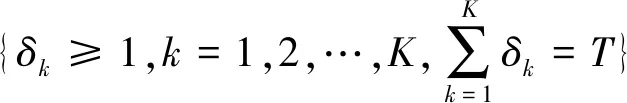
(5)
(6)
(7)
成立,则在下一次发生切换时(t=τh+1),切换律如下:
σ(t)=i, ∀t∈[τh,τh+T) ,
(8)
ifσ(t)=i,∀t>τh+T,如果x′(t)Pi,Kx(t)≤x′(t)Pj,0x(t),∀j=1,2,…i-1,i+1,…,N,
(9)
否则,
(10)
能使具有驻留时间约束T≥2的系统(1)的标称系统渐进稳定。
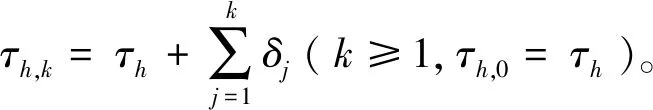
Pσ(t)(t)=
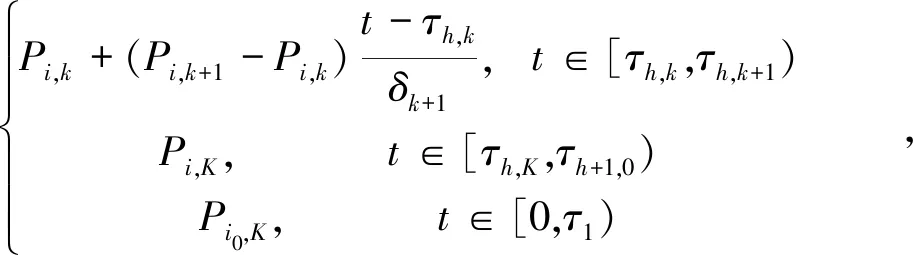
(11)
对于t∈[τh,K,τh+1,0), 可知V(t)=x′(t)Pi,Kx(t),x(t+1)=Aix(t)及

x′(t)Pi,Kx(t)≤x′(t)Pj,0x(t), ∀j=1,2,…,i-1,i+1,…,N。
(12)
因此
(13)
则条件(7)保证了ΔV(t)<0,x(t)≠0,t∈[τh,K,τh+1,0)。
对t∈[τh,k,τh,k+1), 基于引理1,条件(5)和(6), 可得ΔV(t)<0,t∈[τh,k,τh,k+1)。 此外, 由切换律 (8)~(10), 可以发现 Lyapunov 函数在切换点处是非增长的。因此系统(1)的标称系统x(t+1)=Aσ(t)x(t)在切换律(8)~(10)下渐进稳定,定理得证。
3 l2增益
本小节将给出系统(1)(u(t)=0)的渐进稳定性和l2增益性能

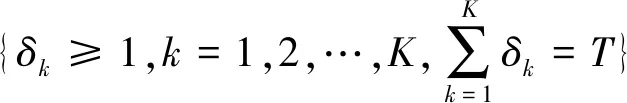

(14)
(15)
(16)
则系统(1)(u(t)=0)在具有驻留时间约束T≥2的切换律(8)~(10)下渐进稳定且具有l2增益性能。
证明如下不等式是等价的。
ΔV(t)+z′(t)z(t)-γ2ω′(t)ω(t)<0,
(17)
(18)
其中P(t)如(11)所示,A,B,C,D如(1)所示。
类似定理1的证明,在驻留时间内,条件(14)和(15)保证了(18)成立。在驻留时间之后和下次切换发生前,由条件(16)可得(18)。此外,根据切换律(8)~(10)可知Lyapunov函数在切换点处是非增长的。因此,条件(14)~(16)和切换律(8)~(10)共同保证了系统(1)(u(t)=0)渐进稳定且具有l2增益性能。定理得证。
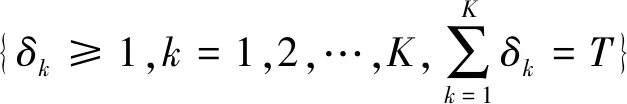
(19)
(20)

(21)
则系统(1)(u(t)=0)在具有驻留时间约束T≥2的切换律(8)~(10)下渐进稳定且具有l2增益性能。
证明由(11)中Pσ(t)(t)的形式,有
Qσ(t)(t)=
(22)
显然如下条件等价
ΔV(t)+z′(t)z(t)-γ2ω′(t)ω(t)<0,
(23)
(24)
(25)
其中Q(t)=P-1(t)。
在驻留时间内,矩阵Qσ(t)(t)从Qi,k线性变化到Qi,k+1, 则将Qi,k和Qi,k+1分别代入(25)可得到条件(19)和(20)。
(26)
由Schurs补可知(26)与(21)等价。证毕。
推论1给出了稳定性和H∞性能的另一个充分条件。由于这些条件能导致凸条件,因此适用于状态反馈控制器设计。
4 状态反馈
设计状态反馈控制器u(t)=Kσ(t)(t)x(t),其中时变控制器增益Ki(t)是待求的。
(27)
结合系统(1)和控制器(27), 有如下闭环切换系统
x(t+1)=(Aσ(t)+B2,σ(t)Kσ(t)(t))x(t)+B1,σ(t)ω(t),x(0)=0,
z(t)=(C1,σ(t)+D12,σ(t)Kσ(t)(t))x(t)+D11,σ(t)ω(t),
(28)
应用推论1,分别用Ai+B2,iKi(t)和C1,i+D12,iKi(t)代替Ai和C1,i, 有下面的结果。
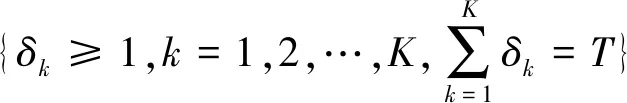

(29)
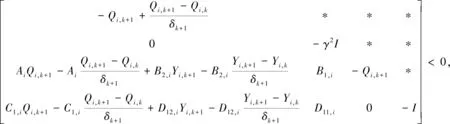
(30)

(31)
则在具有驻留时间约束T≥2的切换律(8)~(10)和控制器(27)下,系统(1)渐进稳定且具有l2增益性能,其中
Ki(t)=

(32)
证明选择
Yσ(t)(t)=
(33)
则由Yi(t)=Ki(t)Qi(t)可得结果。证毕。
5 结 论
本文设计了一个混杂切换律,该切换律保证了闭环切换系统渐进稳定且具有l2增益性能。当驻留时间趋于零时,本文的方法就退化为最小切换,故所提方法为离散切换系统的分析提供了更一般的框架。
