烟草企业生产销售的投入产出分析——以我国某省2019年度数据为例

刘羿勋 孙 扬 王 宁

（1.昆明市烟草公司信息中心，云南 昆明 650051；2.云南财经大学统计与数学学院，云南 昆明 650221）

一、引言

投入产出分析对一个单位的资源利用效率的评价至关重要。但是，专门针对烟草行业的生产销售的资源利用效率的研究并不多见，2015年张晓[1]等利用线性回归分析方法对浏阳市的烟草投入产出要素进行了比较。基于此，可以从同类的分析中借鉴方法，进行专门针对烟草生产销售过程中资源利用效率的分析。在投入产出的分析中，廖虎昌[2-4]等人为了避免DEA方法的局限性，综合运用DEA方法和Malmquist全要素生产力指数方法分别对我国的12个西部省以及省会城市在十年间的水资源利用效率进行了分析；在李志敏[5]的工作中，综合了廖虎昌的方法，选择将主成分分析和DEA数据包络分析相结合对投入产出的资源效率进行分析评价。基于此，本文选取了11个投入指标和6个产出指标，综合运用主成分分析和数据包络分析，完成了对某省的12个州市的烟草生产销售的资源利用率的分析评价。这样的结合方式，有效地规避了这两种方法单独使用时的缺陷，可以包含更多的信息，使得信息利用率较高。

二、研究方法

1.主成分分析

主成分分析方法在1901年由Pearson对非随机变量分析时引入的，并且在1933年由Hotelling将此方法推广到随机向量的情形进行运用。此分析方法的主要目的用较少的变量去解释原本资料中的大部分变异。可以将彼此相关性很高的变量通过此方法转化为彼此独立的变量，从而达到稀释变量的目的，而新得到的变量，就是所谓的主成分。由此可见，这是一种对变量进行降维的分析方法。

在主成分分析中，首先对原始数据进行标准化处理，标准化处理的公式为

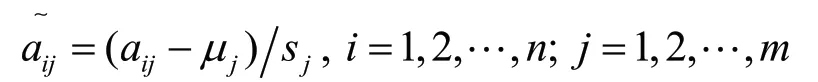
然后计算相关系数矩阵R= (rij)m×m，这是主成分分析的基础，有

上式中，rii= 1，ri j=rji，这里的rij为第i个指标与第j个指标的相关系数值。

接着是计算特征值和特征向量，得到新的变量，即主成分。主要方法如下：

设Zi表示第i个主成分，i= 1,2, … ,p，可以设

上式中1F为第一主成分，2F为第二主成分，……，mF是第m主成分，这些新的指标向量是源自相关系数矩阵的特征值和特征向量组成的。

最后便是选择p(p≤m)个主成分，计算综合评价值。计算特征值λj(j= 1,2, … ,m)的信息贡献率及其累计贡献率。计算公式为

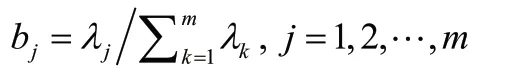
称为主成分Fj的信息贡献率。表示主成分1,2, ,p F F…F的累计贡献率的公式为

一般取pα接近于1时，选择前p个指标变量作为新的主成分。

2.DEA数据包络分析

数据包络分析（Data Envelopment Analysis，DEA）是1978年由美国的运筹学家A.Charnes、W.W.Cooper提出的，主要是通过保持决策单元的输入和输出不变，利用数学规划和统计数据确定相对有效的生产前沿面，通过比较他们的偏离程度来评价他们的相对有效性[6]。DEA的特点是不需要考虑投入产出两者之间内部的函数关系，避免了主观因素，通过投入产出之间的加权和之比来计算效率。在通常情况下认为，输入指标应该大于产出指标的个数，数据应该保证严格非负。如果输入指标和输出指标之间具有较大相关性的话，分析的结果可能不准确。这几点缺陷可以通过主成分分析法进行弥补。主成分分析可以将众多的指标进行降维处理，得到较少的几组相互独立的主成分变量，有利于进行数据包络分析。本文采用了BCC模型，假设规模报酬不变，进而计算每个DMU的相对效率。该模型是基于CCR模型增加了 ∑=1，将综合效率值分解为纯技术效率和规模效率[7]。

3.数据来源和指标选取

本文数据由该省烟草公司提供，出于对于数据的保密，不说明具体名称。同时参考其他文献关于烟草销售效率分析的文献选取评价指标，本文选取了11个投入指标：X1，X2，……，X11，选取了6个产出指标：Y1，Y2，……，6Y，具体指标的名称见下表。

三、分析结果

1.投入指标主成分分析

运用MATLAB对我国某个省份烟草公司2019年的投入指标和产出指标进行主成分的分析。选取11个投入指标，并求出其系数相关矩阵，计算其特征值。下表给出了求得的特征值和各成分的方差贡献率以及累积方差贡献率。

表1 投入产出指标选取表

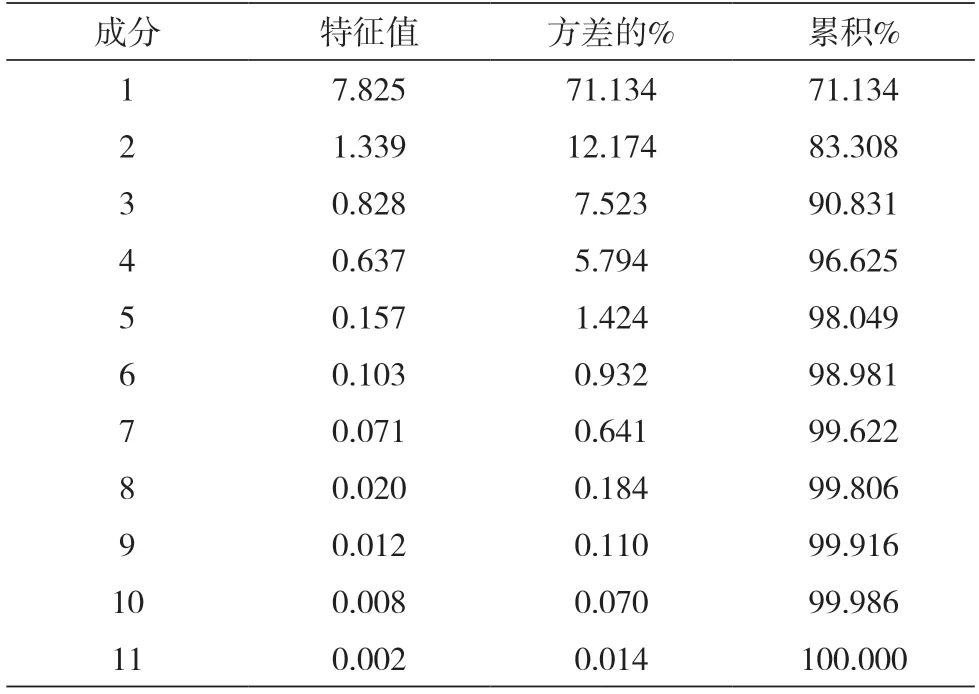
表2 投入指标解释的总方差

从上表中可知，排名前五个成分的累积贡献率方差贡献率都大于1，并且累积贡献率达到了98%。因此，为了分析的准确性，选取前五个成分作为新的主成分，代替原先的11个指标进行分析。

表3为输出的主成分矩阵，由表3可以得到各个主成分的表达式。

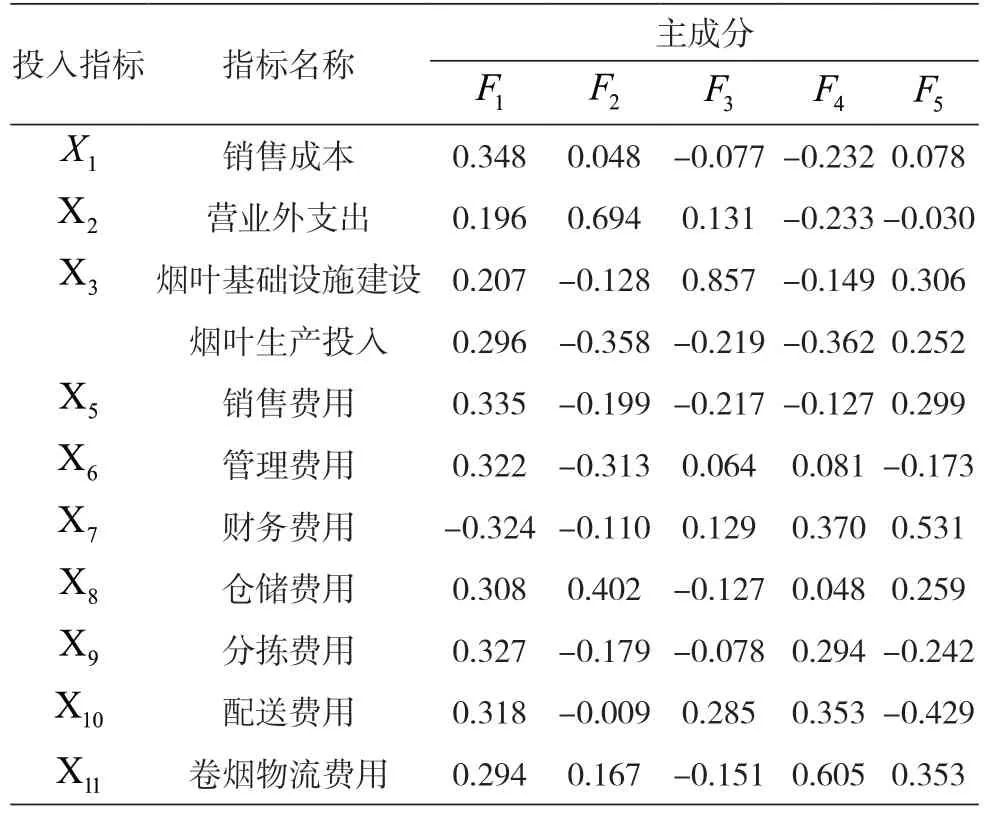
表3 主成分矩阵

根据表3，可以得到选取的5个主成分的表达式。可以计算得出投入指标的综合得分，这是下文的数据包络分析所必需的。表4为投入指标的主成分的得分系数矩阵，从表中可以看出，城市1第一主成分和第二主成分上得分较多，而其他城市甚至在第一主成分上得分为负。从每一个样本在所选取的五个主成分之上的得分来看，大部分的样本数据在每个主成分上的得分分布较为合理。

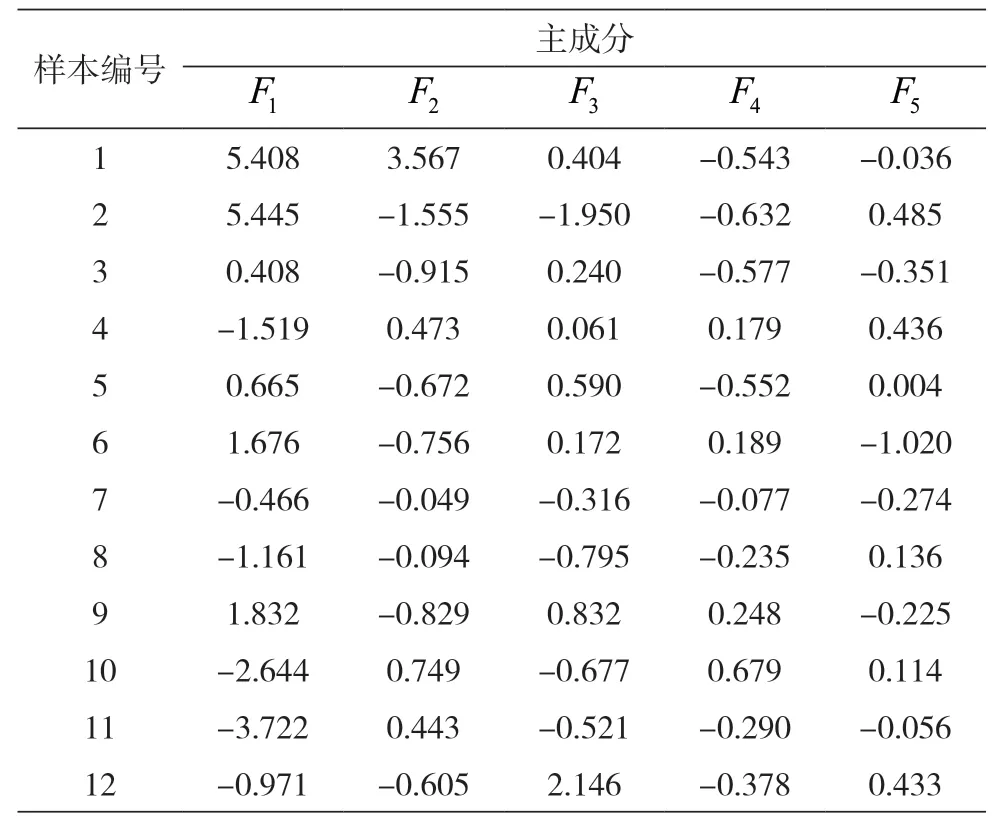
表4 主成分得分系数矩阵

2.产出指标主成分分析

与投入指标的主成分的分析相类似，对于产出指标的主成分分析也得到了相似的结果。表5为产出指标的解释的总方差，里面显示了相关系数矩阵的特征值，以及每个特征值的方差贡献率和累积贡献率。从表中可以看出，前三个主成分的累积贡献率已经达到了95%，因而选取前三个成分作为新的主成分，代替原先的选取的6个产出指标。表6和表7分别为产出指标的主成分矩阵和主成分得分系数矩阵，据此可以写出产出指标的主成分表达式，根据投入指标和产出指标的主成分表达式，可以计算出各个主成分的综合得分值，见表8.

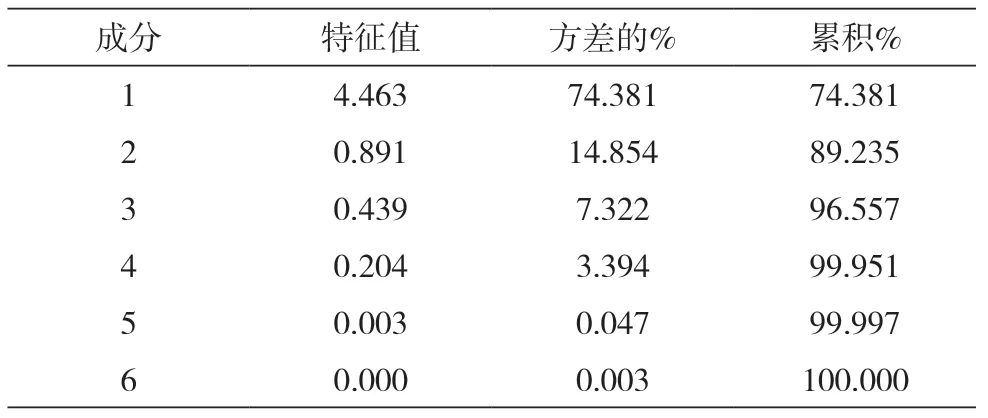
表5 产出指标解释的总方差

表6 主成分矩阵

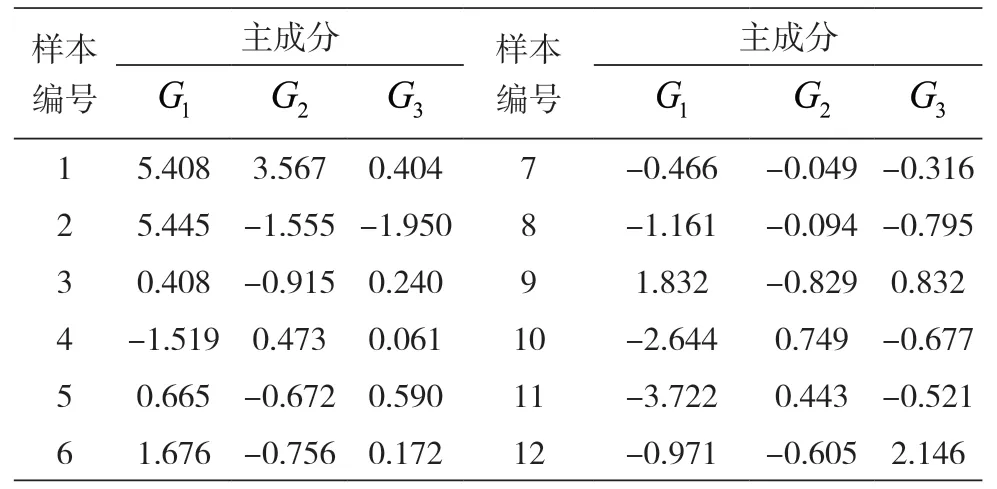
表7 主成分得分系数矩阵

表8 主成分综合得分值

3.投入产出的数据包络分析

通过以上的分析，我们得到了5个投入主成分和3个产出主成分，并且这8个主成分之间是彼此正交的，也就是相互独立的，这为数据包络分析提供了很好的条件。因此，在此基础上，运用MATLAB软件编程进行数据DEA数据包络分析，分析其投入产出的相关状况，得到了表9和表10。

（1）资源的投入产出分析

对资源的投入产出分析可以从两个角度进行，一个是基于决策结果进行分析；另一个是基于无效单元投影进行分析。先基于表9进行决策结果分析。

表9 12个城市烟草销售中的资源利用效率

v注：表中的drs表示规模报酬递减，irs表示规模报酬递增，-表示规模报酬不变。

①从综合效率分析

基于表9，从综合效率值的角度看，城市1-3、5-7、9、10和12都DEA有效。需要指出的是，这其中城市的排名顺序是基于该城市的经济体量由大到小进行排序的。可以看到，这9个城市中既有经济发达的城市，也有经济欠发达的地区，这说明烟草生产销售的利用率与经济并没有直接的关联。这里的效率值是一个相对有效值，并不是一个绝对效率，他只是表示每个地区的经营公司对资源的投入产出利用比率。这也是为什么在经济欠发达的地区依然能够DEA有效。

②从技术效率和规模效率分析

接下来结合无效单元投影的角度对技术效率和规模效率进行分析。表10为无效单元的投入冗余和产出不足分析数据表格。

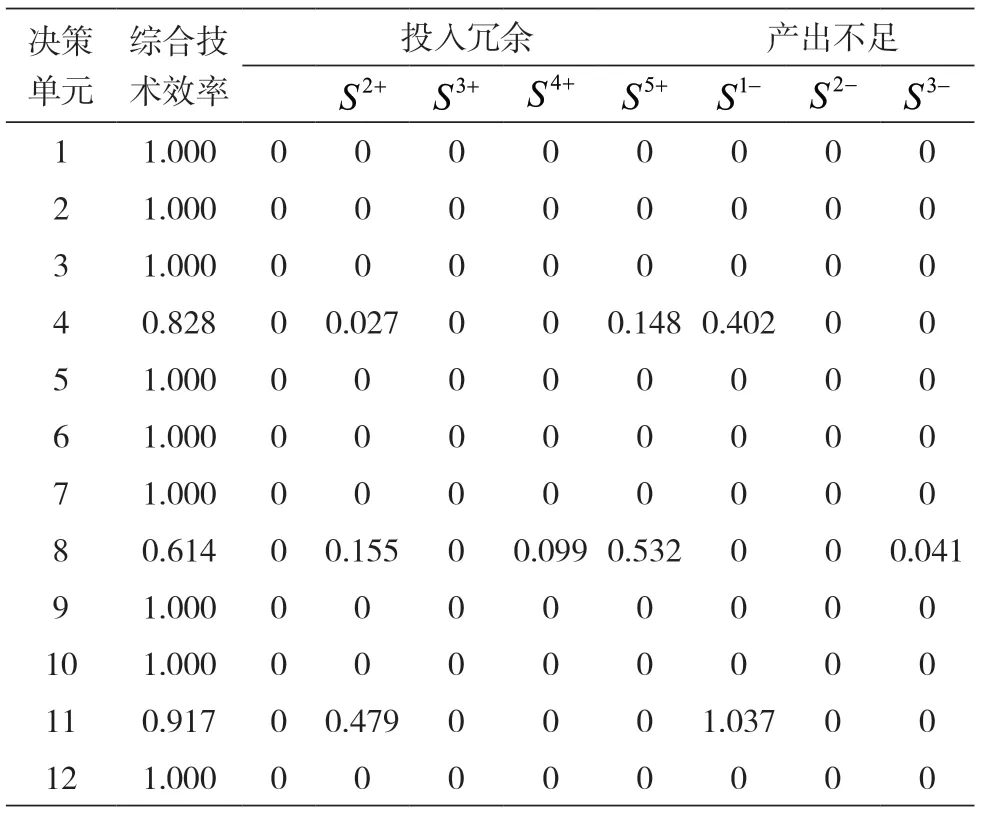
表10 无效单元的投入产出分析

从表9中还可以知道，在分析的样本中，还有3个城市没有达到DEA有效，并且可以看到的是，这四个城市的规模收益的状态都为递减状态。这说明，即使再加大规模，也不会有更好的结果，需要做的是从纯技术效率和规模效率两方面进行调整。城市8和城市11，他们的技术效率都达到了DEA有效，说明技术较为成熟，但是综合效率值并没有达到有效，以及规模效率值也未达到，根据规模收益的数据显示，如果盲目加大规模，可能会导致规模效率降低。因此，城市8和城市11应该加大生产投入，并且提高产能，以期改善规模效率值。结合技术效率和规模效率，城市4，其三项指标都没有达到有效，并且规模收益的状态还显示为递减状态，因而可以适当地通过提高产能和加大投入来提高技术规模的效率，以期达到综合效率有效。

（2）提高资源利用率的对策建议

从总体的分析结果来看，大部分的城市在烟草生产与销售的资源利用上已经达到了一个DEA有效的水平，这表明该省份的烟草发展是比较成熟的。对于个别的州市地区存在技术效率的提高问题，可以向其他的综合效率达标的城市学习，但是对于规模效率需要提高的问题，不能够盲目地扩大规模。从总体上来看，不断向优秀者学习，优化产业结构，就能够充分地利用好资源，使综合效率达到比较理想的状态。

四、结语

本文利用主成分分析与DEA数据包络分析相结合的方法，先对12个州市的数据进行主成分分析，得到几组相互独立的主成分变量，然后利用DEA数据包络分析的方法对该省的烟草生产销售的资源利用率进行了分析和评价。从方法上看，主成分分析和数据包络分析实现了互补，使分析更加地贴合，分析的结果也是可靠的。在最后部分给出的对策和建议，对相关州市的烟草产业的发展，可以起到优化产业结构的作用，对生产具有一定的指导意义。