纤维多孔介质介观尺度结构对其真空绝热性能的影响
2021-03-31陆家希阚安康朱文兵袁野百合
陆家希,曹 丹,阚安康,朱文兵,袁野百合
(上海海事大学商船学院, 上海201306)
随着国家节能减排战略的持续推进,绝热行业的标准及市场规模逐年提升,而真空绝热板(Vacu⁃um insulation panel, VIP)因其优异的绝热性能,被认为是最有研究和运用前景的绝热材料之一。为提升VIP 的绝热性能,延长其使用寿命,近几十年来,人们对各种VIP 芯材进行了研究[1⁃5]。其中,纤维多孔介质(Fibrous porous material, FPM)因具有较高热稳定性、较低的成本以及在高真空度下优异的绝热性能,备受青睐[6]。揭示FPM 内气固两相共轭传热机理,对进一步提高玻璃纤维芯材VIP的绝热性能、降低其生产成本,具有重要意义。
FPM 内部的传热强度及其有效导热系数(Ef⁃fective thermal conductivity, ETC)的大小不仅取决于各组分的物理性质和孔隙率(密度),还取决于其介观结构特征。而事实上,鉴于多孔介质的不规则特性,用实验方法直接控制或测量其介观结构是极其困难的。为研究介观结构特征对多孔介质传热的影响,诸多专家学者一直都在积极寻求一种能够用几何参数随机生成复杂孔隙结构的方法。由于其网格化的特点,这一方法很容易与格子Boltzmann 方法(Lattice⁃Boltzmann method, LBM)相结合。LBM 被广泛用于模拟多孔介质中的传热传质过程[7⁃9],从本质上讲,它作为一种介观尺度的数值模拟方法,在求解复杂流动时具有很大优势:一方面,LBM 不需要复杂的边界条件来保证气固界面能量方程的连续性;另一方面,并行算法可以很容易地与其结合以求解计算量巨大的复杂多孔结构[10]。比如,Chen 等[11]采用基于扫描电镜图像(Scanning electron micrographs, SEM)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo, MCMC)方法重建了页岩的三维纳米结构,并运用LBM 算法研究了孔隙流动和Knudsen 扩散。Wang 等[12]提出了一种四参数结构生成算法(Quartet structure generation set, QSGS),并利用LBM 模型研究了孔隙结构的导热系数,结果与实验数据的对比表明该方法具有较高的精度,可用于多相多孔结构的重建[13⁃14]。基 于Wang 等 的 算 法,Hussain 等[15]进 一 步提出了一种宏观⁃微观孔随机生成方法,并将其应用于多孔介质有效质量扩散系数的模拟,与单纯基于物理参数和网格的QSGS 方法相比,该方法生成的微观结构更接近于实际孔隙的几何特征。此外,Liu 等[16]利用层析重建方法对多孔介质进行了重建,并进行了孔隙尺度LBM 模拟,推导了流动与传热的关系式。同样,Qu 等[17]也引入随机生成方法,提高了气凝胶多孔结构导热系数的模拟精度。
尽管这些生成方法已经得到了广泛的验证,并对于各种多孔介质(如黏土、气凝胶、二氧化硅等)的重建和生成具有很高的实用性,但由于纤维的细长形状以及由此产生的各向异性,以上方法很难直接应用于FPM。2009 年,Wang 等[18]首次对三维纤维材料的ETC 进行了研究,提出了一种三维纤维结构生成方法,并结合LBM 对碳纤维复合材料的导热系数进行了模拟。与此同时,He 等[19]还利用该方法分析了微观结构对纤维材料有效热扩散系数的影响,包括结构各向异性、体系含水量、微观结构形态和分层空间。
在上述研究基础上,本文提出了一种改进的FPM 三维结构随机生成算法,减少纤维的穿插,改善其分布,并采用D3Q19⁃LBM 方法求解了其在不同真空度下的有效导热系数,详细讨论了FPM 的介观结构特征(即直径和方向角)对ETC 的影响。
1 纤维介观结构生成方法
以两相(纤维/空气)FPM 为对象,结合图1 所示电镜扫描图像获得的介观结构参数,本文所改进的FPM 生成算法的流程图如图2(a)所示,具体生成过程可以描述为:
(1)初始化将所有网格节点(Nx×Ny×Nz)为气相,每个格子步长为1 μm。
(2)基于给定的核心分布概率cd,将一个非固相的点随机生成为固相生长核心(x0,y0,z0)。
(3)给出倾角α 和方位角β,以确定纤维的生长方向。α 表示纤维与z 轴之间的角度,β 表示纤维与y 轴在平面z 中的投影角;给出长度lf和直径df以确定纤维几何结构,如图2(b)所示。

(5)重 复 步 骤(2~4),直 到 孔 隙 率 达 到 给定值ε。
法向距离d(x,y,z)和轴向距离l(x,y,z)可以表示为
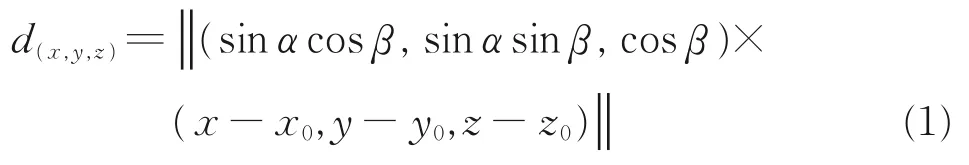

图1 纤维多孔介质的SEM 图像(放大1 000 倍)Fig.1 SEM image of FPM (Magnified 1 000 times)
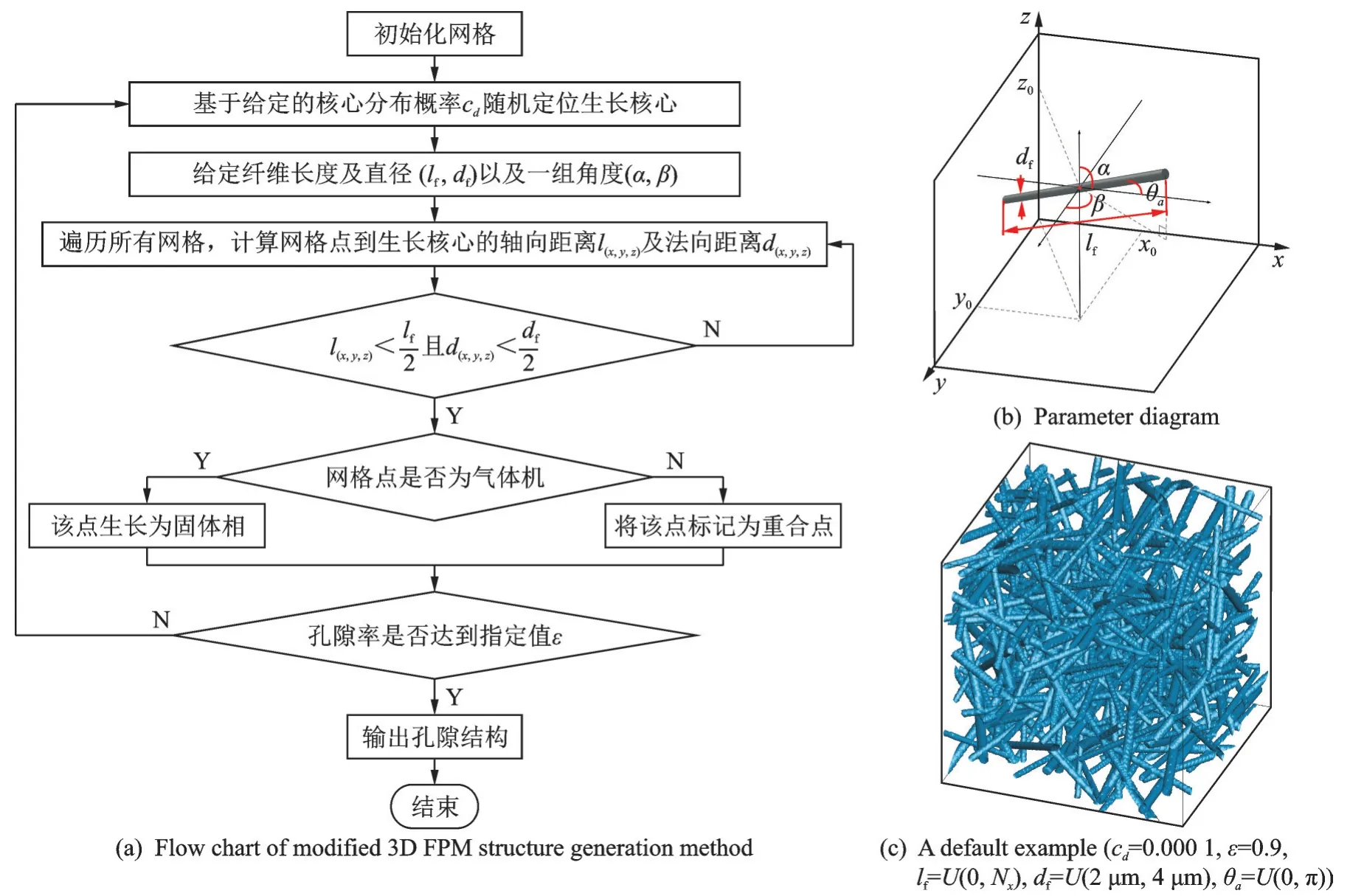
图2 纤维介观结构生成过程Fig.2 Mesoscopic structure generation process of FPM

如上所述,FPM 介观结构的生成过程是基于6个参数而进行的,分别是:芯分布概率cd、角度α 和β、长度lf、直径df和孔隙率ε。步骤(3)中的lf、df、α以及β 既可以为常数,也可以是基于均匀、正态或任何其他分布函数的随机值。本文lf和df分别被默认为在[0,Nx]和[2 μm,4 μm]内满足均匀分布的随机值。
为便于讨论,文中引入了方向角θa=π/2 -arcsin(sinα∙sinβ),其物理意义表示总传热方向与纤维长度方向的夹角,该方向角也默认为满足[0,π]内均匀分布的随机值。
如图1 所示FPM 中的纤维应该相互交织而不是相互穿插的,本文定义了一个穿插率φi来描述一根纤维在生成过程中穿过另一根纤维的概率

式中nf和ni分别为纤维总数和标记的重合点的数量。由图3 可知,随着网格数量的增加,穿插率逐渐减小并在Nx<200 时趋于稳定。综合考虑穿插率、计算效率以及后续LBM 算法的计算稳定性和精度,将计算域设置为200×200×200 的网格,默认生成结果如图2(c)所示。图4 为用本文改进的生成方法生成的具有不同纤维直径和方向角的FPM 介观结构。

图3 穿插率的网格依赖性Fig.3 Grid dependence of interpolation rate


图4 基于改进的随机结构生成方法生成的不同参数的FPM 介观结构(cd=0.000 1,ε=0.9,lf=default)Fig.4 Mesoscopic structures of FPM with different parame⁃ters generated by the modified random structure gen⁃eration method (cd=0.000 1,ε=0.9,lf=default)
2 物理方法与数值求解
2.1 有效导热系数
多孔介质的有效导热系数由以下组分藕合而成
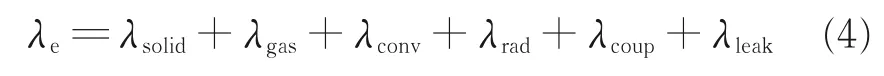
式中:λsolid及λgas分别表示固相和气相的导热系数;λleak表示由热泄漏引起的导热系数增量,在保温材料中可忽略不计;λcoup表示耦合传热的导热系数,一般忽略不计[20];λconv表示对流换热的等效导热系数,以往的研究表明,在孔隙尺寸小于1 mm 或纤维密度大于20 kg/m3时,对流换热可以忽略不计[21]。另外,出于计算效率的考虑,辐射导热系数直接采用式(5)计算[22]

式中:KB=1.38×10-23J∙K-1;L 为冷热板之间的距离;Tm为平均温度;e 为纤维材料的发射率。
由此可得,将LBM 计算域划分为固体区域(纤维)Ωs和气体区域Ωg(空气),如图5 所示。不同的区域具有不同的固有物理属性,如密度ρ、热容cp和导热系数λ。
根据以上分析,本文采用如下共轭传热控制方程

式中:cp为比热容;T 为网格点温度;t 为离散时间;λ 为导热系数。
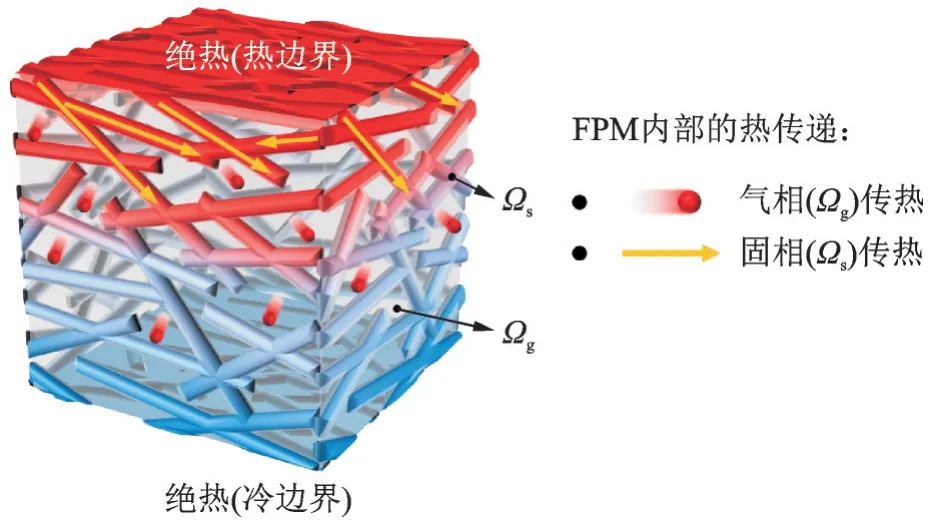
图5 LBM 计算域示意图Fig.5 Schematic diagram of LBM computing domain
2.2 格子玻尔兹曼求解器
本文采用的D3Q19模型如图6 所示。
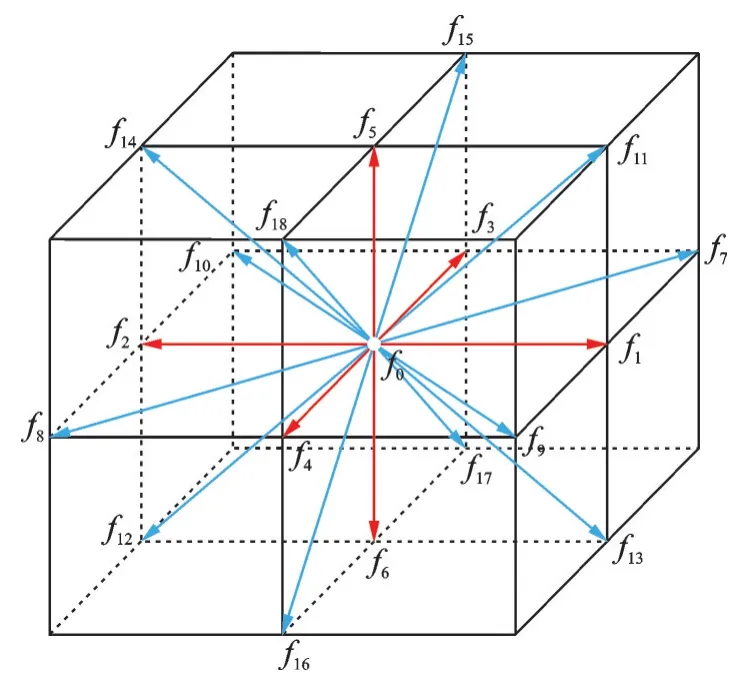
图6 D3Q19模型示意图Fig.6 Schematic diagram of D3Q19⁃LBM model
碰撞过程可表示为

流动过程可表示为

式中:fi为位置x 处在离散方向i 上的温度演化函数;ei为离散速度;δt 为时间步长;τ 为无量纲弛豫时间;feqi为局部平衡函数,因未考虑气相的对流和传质,所以气固两相的feqi都可由式(9~10)给出

式中:T(x,t)为局部温度:wi为权重系数,取值如下

D3Q19模型的离散速度可以表示为

无量纲弛豫时间可表示为
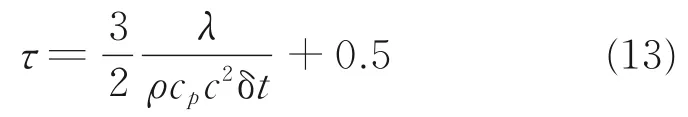
固相和气相的无量纲弛豫时间都可用方程(13)表示。 为了反映宏观上的热流密度,ρcp取1[23⁃24]。
对于气相来说,气体分子在FPM 内的运动受到高度限制,因此微孔内的气体导热系数λ 与自由空间内的λg0不同Knudsen 数下有所不同

式中:λg0=0.024 2 W∙m-1∙K-1;βe为描述气体分子与固体边界之间能量传递的系数,由普朗特数和热扩散系数决定[25⁃26],对于空气而言,βe通常取1.63;Kn 为Knudsen 数,可用式(15)表示
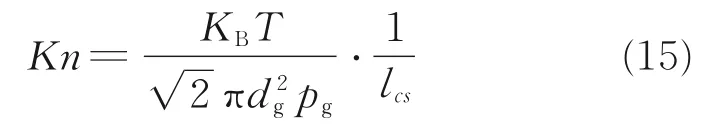
式中:KB=1.38×10-23J∙K-1;dg=3.72×10-10m;lcs为纤维多孔介质的特征孔径,本文lcs=6.15dfε3.35。
有效导热系数可通过方程(16)求解
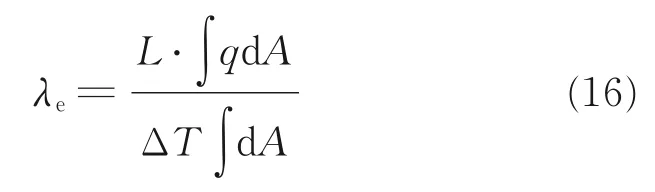
式中:∆T 为冷板和热板之间的温差;q 为热流密度,可根据fi计算得到
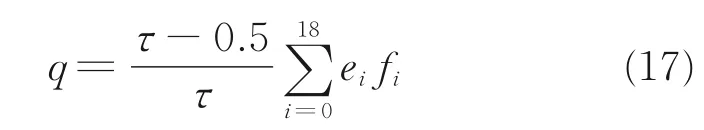
2.3 边界条件
对于传热问题,本文采用Zou 和He[27]提出的非平衡分布反弹格式来处理等温边界
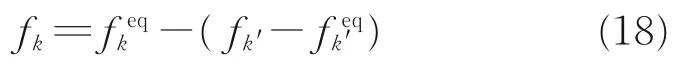
式中下标k 代表未知方向,而k'则表示对应的相反方向。
绝热边界采用反射格式[28]

详细的边界处理条件如表1 和图7 所示。

表1 具体边界处理格式Table 1 Specific boundary treatment format
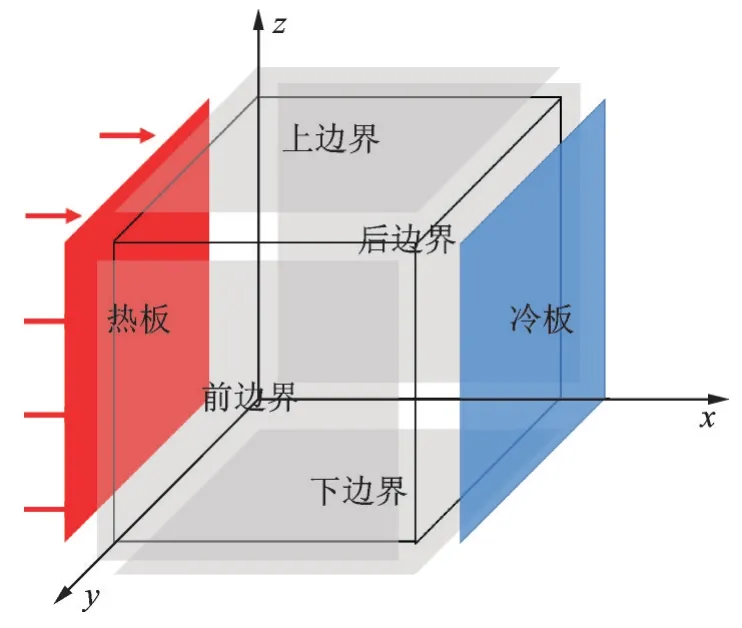
图7 边界条件示意图Fig.7 Boundary conditions
3 对比及验证
本文模拟了FPM 的ETC 随压力pg的变化情况,以验证改进的纤维随机结构生成方法和D3Q19⁃LBM 的有效性。纤维直径被假设为在[7 μm,12 μm]内满足均匀分布。
模拟结果与已发表数据的对比如图8 所示。结果表明,随气体压力的增加,λe的变化都可分为3个 阶 段:当pg<50 Pa 时,λe基 本 稳 定 在 理 想 的 低值( <4 mW∙m-1∙K-1);但随着压力的进一步增加,λe迅速增加;当pg>104Pa 时,λe趋于稳定,不再随压力的升高而增加。模拟结果与已发表数据基本相符,它们之间的细微偏差可归因于以下原因:(1)在本研究中,特征孔径代替精确的局部孔径进行LBM 迭代;(2)辐射导热系数被视为一个固定值。

图8 模拟结果与已发表数据之间的比较Fig.8 Comparison of simulation results with published data
4 结果与讨论
本文详细讨论了真空度、纤维直径和纤维方向角对FPM 的绝热性能,尤其对有效导热系数的影响。
4.1 气体压力和纤维直径对绝热性能的影响
真空度在FPM 芯材真空绝热板的传热过程中起着关键作用。以往的研究表明,FPM 芯材在极低压力(特别是≤50 Pa)下具有优异的绝热性能,但对内部压力的升高也更为敏感[31⁃32]。这种特性可能与其更高的开孔率和更大的孔径(相较于二氧化硅或气凝胶材料)有关。因此,本文选取了5 种直径,即df=1、2、4、6 和8 μm 的FPM 作为研究对象。用相同的孔隙率(ε=0.9)生成了5 种直径对应的介观结构,其余参数设为默认值(cd=0.000 1,lf=U(0,Nx),θa=U(0,π))。
如图9 所示,虽然不同纤维直径的FPM,其ETC 在压力pg变化时具有相似的趋势,但其对压力 的 敏 感 程 度 不 同。若 以λe=8 mW∙m-1∙K-1作为失效阈值,df=8 μm 的FPM 在pg=100 Pa 时就达到阈值。纤维直径越细,则失效压力越高。由图9 还 可 以 发 现,在pg=1 Pa 时,df=8 μm 和df=1 μm 的ETC 差 值 达 到 了1.41 mW∙m-1∙K-1。这 种明显的差距同样可在pg=105Pa 下观察到。由图10 可知,该现象可以由Knudsen 扩散原理来解释:FPM 孔隙特征尺寸(lcs)与直径密切相关,图10(a)中所示介观结构具有比图10(b)中所示具有更细的纤维直径,在相同孔隙率下具有更大的纤维数量。故而图10(a)所示结构比图10(b)所示具有更致密的纤维排列、更小的孔径和更均匀的孔隙分布。根据Knudsen 扩散理论,较小的孔径意味着较小的分子平均自由程,可大大抑制气体热传导。具有较小纤维直径的FPM(图10(a)和图10(c))在真空或大气压下表现出更均匀的等温线分布,这表明更小的纤维直径对于提升FPM 的绝热性能、降低热桥效应等具有重要意义。
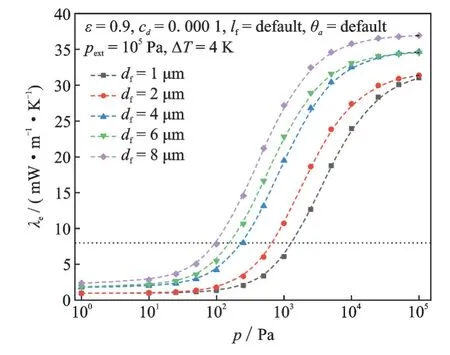
图9 不同df 下λe 随压力变化规律Fig.9 Variation of effective thermal conductivity with pres⁃sure under different df
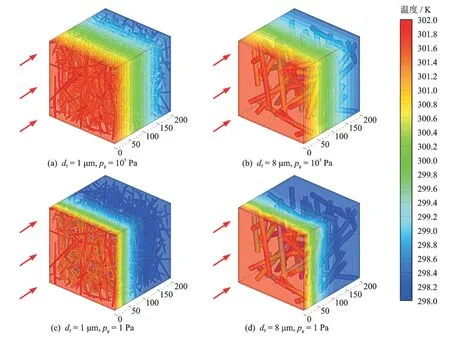
图10 不同直径的FPM 结构在两种压力条件下的稳态温度分布(ε=0.9, cd=0.000 1,lf=default, θa=default)Fig.10 Steady state temperature distribution of FPM structures with different diameters under two pressure conditions (ε=0.9, cd=0.000 1,lf=default, θa=default)
4.2 方向角对保温性能的影响
为便于论述,本文定义了纤维长度的两个典型生长方向,即垂直于传热方向和平行于传热方向。由图11 可知,λe与θa呈负相关,并在θa达到90°时,λe达到极小值。由图12 知,固相的传热是高度定向的,即沿着纤维长度的方向。当θa达到90°时,热通道主要沿着垂直于传热方向的界面,而θa减小时,热通道随即变短,传热加强,温度场发育更广。Chen 等[33]的实验也得出了相同结论。在低压下,λe的变化范围扩大,是因为低压下气相传热被大大抑制,固相传热占主导作用,从而导致固相的导热系数对ETC 的影响更为显著。

图11 ETC 随方向角的变化规律Fig.11 Dependence of ETC on the orientation angle
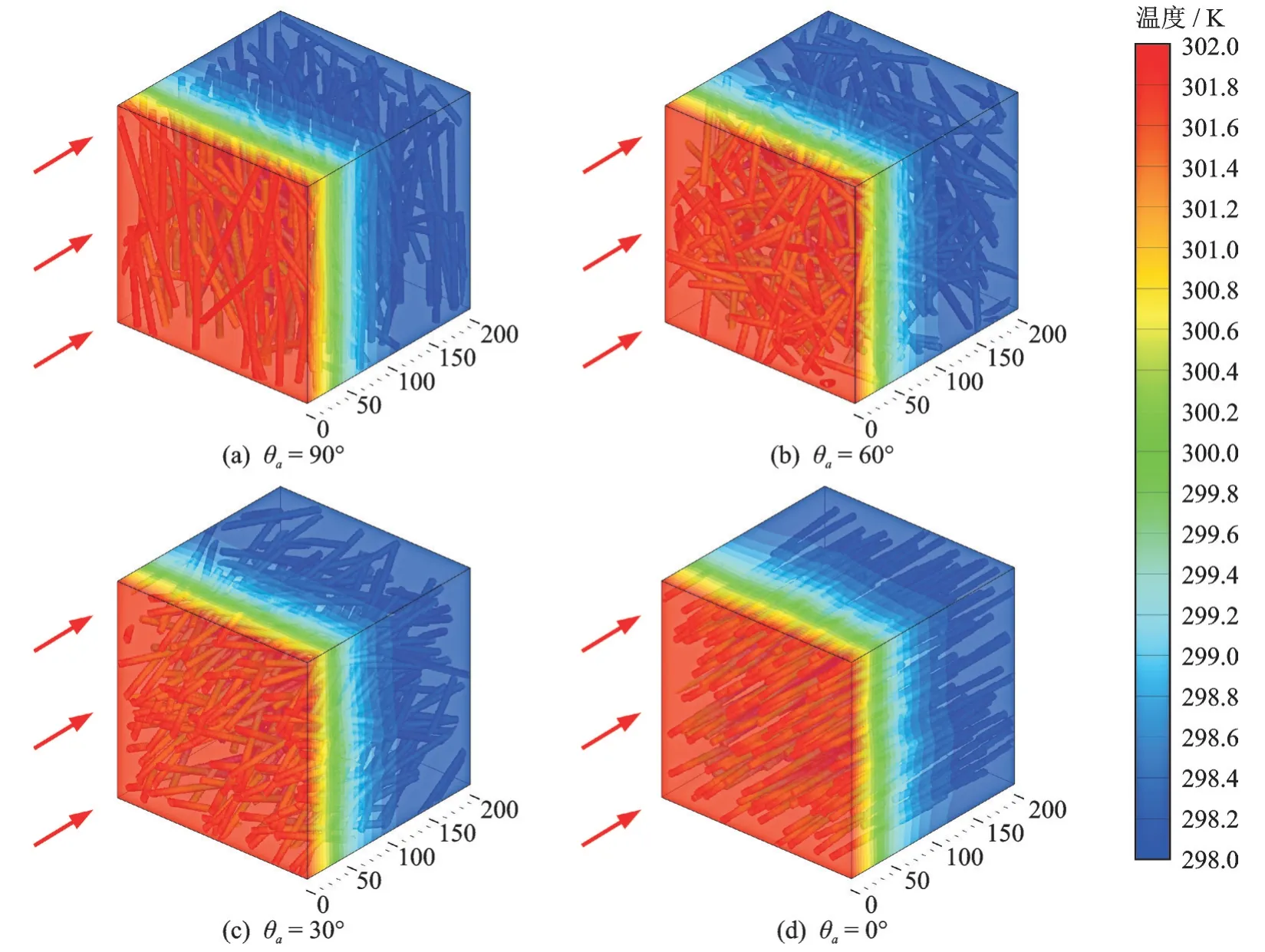
图12 不同方向角的4 种FPM 结构在pg=1 Pa 下的稳态温度分布(ε=0.9, cd=0.000 1,lf=default, df=4 μm, pg=1 Pa)Fig.12 Steady state temperature distribution of four FPM structures with different orientations under pressure of 1 Pa (ε=0.9,cd=0.000 1,lf=default, df=4 μm, pg=1 Pa)
5 结 论
本文在改进3D 纤维多孔结构生成方法的基础上,结合D3Q19格子Boltzmann 方法,构建了一种用于研究纤维多孔介质真空绝热性能的数值计算模型,详细讨论了介观结构对有效导热系数的影响因素。改进的生成方法可有效减少纤维穿插,穿插率降低至3.1%以内,更接近真实纤维排布结构。与实验数据及理论值相比,模型具有较高的可靠性,可作为纤维结构优化的依据。模拟结果总结如下:
(1)揭示了有效导热系数随纤维直径变化的规律。在1~8 μm 的区间内,纤维多孔介质介观结构直径越细,则孔径越小,有效导热系数越小,且在较高气压下保持较低有效导热系数的能力越强。
(2)有效导热系数受纤维多孔介质内部纤维方向角的影响。当方向角达到90°时,有效导热系数值最小,即纤维长度方向与传热方向越一致,传热能力越强,绝热性能越差。
