弱撞击对接机构动力学特性建模

陈传志，汪 捷，陈金宝，邓卫华，崔继云

（1.南京航空航天大学航天学院，南京211106；2.深空星表探测机构技术工业和信息化部重点实验室，南京211106；3.航天东方红卫星有限公司，北京100094）

弱撞击对接机构（Low impact docking mecha⁃nism, LIDM）是当前空间交会对接任务中最具潜力的新型对接机构之一，为中国未来的载人航天工程、探月工程以及国际空间站的建立与对接等提供很大的应用价值[1]。为保证空间对接机构在任务过程中精准地完成捕获对接，对于空间对接机构在捕获阶段工况下的动力学建模与分析是十分有必要的。通过系统建立的动力学模型，可以从理论上研究力与力矩对于运动之间的关系，掌握运动下驱动力的变化幅度，了解捕获阶段的运动学关系，为后续的动力学机械特性研究与尺寸优化设计等提供基础。

早期的航天器对接任务并没有考虑对接机构的具体结构形式，只是单纯地把对接机构当成一个铰链或是弹簧阻尼等去考虑，例如Grubin[2]将航天器视为刚体，而对接机构直接视为一个接触点，分析了对接过程中不同阶段的接触力大小。随着对接动力学的发展，后续的学者逐步开始考虑对接机构本身对于交会对接任务中的影响，例如Ward等[3]在二维平面中分析了在不同的初始对接工况下，“锥⁃杆”式对接机构圆锥导引面对于捕获阶段的作用。国内学者对于对接动力学的研究起步于20 世纪80 年代。洪嘉振等[4]在多体系统的碰撞动力学、柔性多体系统动力学的建模理论、变拓扑多体系统动力学等研究领域做出重要贡献，最早利用经典碰撞理论分析了空间对接。陈占涛[5]开展了异体同构周边式液压对接机构的动力学分析，并分析了带有挠性附件的刚体飞船对对接碰撞的动力学响应研究。近些年来涉及对接机构的建模，多是针对不同类型的对接机构在捕获、对接碰撞、刚性锁定阶段的多刚体动力学方程建模、仿真与试验设计。关英姿等[6]分析了航天器对接过程中的缓冲阶段，建立接触力模型并将周边式对接机构看作等效缓冲弹簧阻尼系统建立动力学模型。时军委等[7]以神舟飞船的对接机构为研究对象，介绍了工程领域中研制阶段仿真的任务规划，给出了对接机构在仿真分析过程中的捕获缓冲参数设计、数字样机、对接过程动力学仿真评估、试验验证与模型修正，以及对接动力学试验等。王晓雪[8]基于拉格朗日方程对一类非合作卫星目标对接捕获机构建立了动力学模型。尤超蓝等[9]以内翻式的异体同构周边式对接机构为研究对象，分析了机构在对接捕获阶段的三体力元模型。李隆球等[10]设计了一种轻小型三臂型非合作目标卫星对接机构并进行了相关运动学与机械臂的动力学分析。

空间弱撞击对接机构利用力反馈柔顺控制技术代替传统的差动式缓冲组件，可以说，其柔顺控制技术的基础在于完整的捕获动力学模型上，控制系统的数字模型可以由动力学模型直接提供。为了保证空间对接机构在任务过程中精准地完成捕获对接，需要研究空间对接机构在捕获阶段工况下的动力学建模过程。本文基于空间弱撞击式对接机构的构型特征，利用拉格朗日方程建立其捕获动力学方程，了解捕获阶段的力与运动的传递关系。利用MATLAB 计算出相关的动力学参数，并与ADAMS 联合，验证了模型的正确性。驱动力的计算分析研究对于弱撞击对接机构本体的机械结构、控制系统研发优化等工作提供理论与数据支持，为论文后续优化设计与控制算法提供基础的数字模型。

1 运动学模型建立

1.1 弱撞击对接机构结构概述

弱撞击式对接机构在机械结构上包含了负载环（Load sensing ring, LSR）、六维力传感器、驱动臂系统、电磁捕获系统等，如图1 所示。LIDM 拥有一个六自由度动平台，即对接环，通过控制6 根执行推杆的伸出量来完成期望的对接环位姿。

图1 弱撞击对接机构Fig.1 Low impact docking mechanism

六维力传感器实时监控捕获阶段的碰撞力/力矩,并以作用于LSR 质心处的时变载荷形式反馈。因此，将捕获过程中弱撞击对接机构处产生的碰撞力简化为作用于对接环质心处的时变载荷。

1.2 负载传感环的位置姿态描述

描述弱撞击对接机构的机构参数，抽象结构简图分别如图2 和3 所示。建立两个坐标系{a}和{A}：动坐标系{a}固定在负载传感环上，基坐标系{A}固联于基环上。具体表述如下：机构的基座平台与LSR 对接环分别分布有6 个虎克铰，相应上下铰链连接有驱动臂执行推杆。每根执行推杆包含有一个移动副。现以基座平台的中心点O 建立基坐标系O⁃XYZ，Z 轴垂直基座平台的基准平面指向LSR，X 轴与Y 轴在基座平台基准平面，构成右手坐标系。以LSR 环心O1为中心，建立随体坐标系O1⁃X1Y1Z1，Z 轴平行LSR 纵向对称轴朝外，与X 轴和Y 轴构成右手坐标系。记O⁃XYZ 6 个铰链点为A1～A6，O1⁃X1Y1Z16 个 铰 链 点 为a1～a6，这12 个 铰链点在各坐标系中是固定的。现为研究方便，令A1～A6处于半径为R0的外接圆上，a1～a6处于半径为r0的外接圆上，且相邻较近的一对铰链点与中心的结构角分别记为js、jx，且沿中心对称分布。

图2 弱撞击对接机构坐标系Fig.2 Coordinate system of low impact docking mechanism

图3 结构简图Fig.3 Structure diagram

{a}在{A}中的位置由位置向量P=[x, y, z]T表示，即{a}的基点在{A}中的位置表示。{a}在{A}中的姿态由旋转矩阵θ=[α, β, γ]T表示。卡尔丹角α、β、γ 的物理意义：将{a}的初始姿态与参考系{A}重合，首先将{a}绕X 轴转α 角，再绕Y 轴转β 角，最后绕Z 转γ 角。因为三次旋转都是相对于固定坐标系{A}而言的，故得相应的旋转矩阵R 如下

同时负载传感环的位姿参数矩阵可以表示为

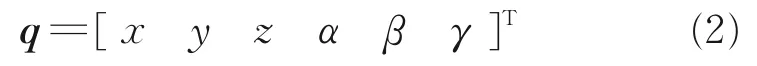
1.3 驱动臂的位置姿态描述

LIDM 各驱动臂分支结构组成相同，为更清晰地描述仅取一个驱动臂分支完成运动学分析，单驱动臂分支的结构模型如图4 所示。O 为LIDM 基座的中心，O1为LSR 的中心，ai与Ai分别为驱动臂电动推杆与LSR 和电动缸与基座的铰接中心。在驱动臂电动推杆、电动缸的质心位置建立参考坐标系O3⁃X3Y3Z3和O2⁃X2Y2Z2。参考坐标系O3⁃X3Y3Z3和O2⁃X2Y2Z2各个轴平行，其中Z2和Z3轴沿驱动臂轴线方向由根部铰链点指向顶部铰链点，X2和X3轴平行于虎克铰链的旋转轴，Y2和Y3轴符合右手法则。

图4 驱动臂坐标系简图Fig.4 Driving arm coordinate system diagram

现在需求出驱动臂电动推杆、电动缸质心坐标系到基坐标系的旋转变换矩阵Ti。由于参考坐标系O3⁃X3Y3Z3和O2⁃X2Y2Z2各个轴平行，则旋转变换矩阵是一致的。

这里从1.1 节的坐标系规定中可以得出，由动坐标系相对基坐标系的姿态易得相应驱动臂所在方向上的单位向量ui

式中：P 为{a}相对于{A}中的位置矢量；ai为顶部铰链点在{a}中的坐标表示；Ai为根部铰链点在{A}中的坐标表示；R 为对应的旋转矩阵。

这里单位向量ui与驱动臂电动推杆、电动缸质心坐标系的Z 轴同向，可以看成是由在基坐标系下沿Z 轴的单位向量eZ绕某一旋转轴旋转一定角度来得到相应的单位向量ui。

旋转角度由两向量的点乘获得

旋转轴由两向量的叉乘获得

将Li单位化即可得到其相对于基坐标系的方向余弦p1、p2、p3。

由方向余弦与转角信息可以求得欧拉参数

方向余弦矩阵可以由欧拉参数表示

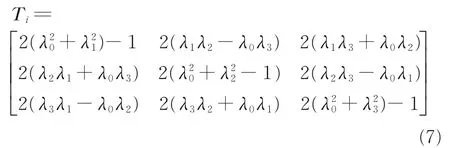
1.4 驱动臂伸缩速度与负载传感环之间的运动学关系

ai为顶部铰链点在{a}中的坐标表示，Ai为根部铰链点在{A}中的坐标表示。驱动臂的方向矢量li满足

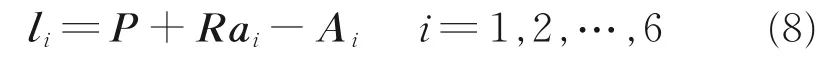
将式（8）展开可以得到

驱动臂当前伸缩长度表示为

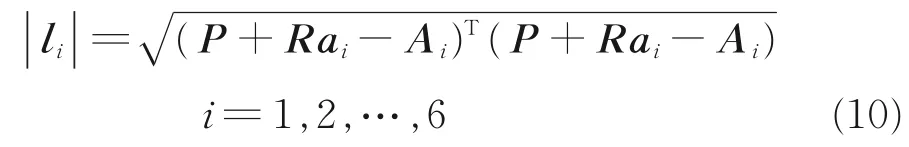
驱动臂与负载传感环之间的速度关系可以由一个运动雅克比矩阵表示[11]

1.5 驱动臂顶部铰链点速度、角速度与负载传感环之间的运动学关系

负载传感环姿态角参数α、β、γ 采用了卡尔丹角描述方法，其对时间的倒数并不是平台的角速度，但它们之间有式（13，14）成立[12]

式中ω0表示负载传感环在{A}中的空间角速度。

因此，以负载环质心为参考点，各驱动臂顶部铰链的速度可由负载环的质心速度与相对角速度合成表示

式中v0为负载环质心速度。

如果设第i 根推杆的角速度为ωi，第i 根推杆的杆长为li，以根部铰链为参考点，各驱动臂顶部铰链速度又可以表示为

显然，式(15)和(16)等价，通过联立可以得到

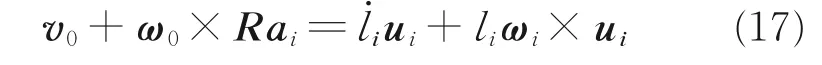
不考虑驱动臂推杆绕自身轴线的转动，则有

成立。

对式(17)左右同时叉乘单位向量ui，并代入式(18)进行化简，可以得到各驱动臂推杆角速度表达式式中：ui为对应驱动臂的单位向量；vsi为对应顶部铰链的速度矢量；li为对应驱动臂的长度大小。注意：该角速度是在基坐标系下的形式。

1.6 驱动臂电动推杆、电动缸杆质心在基坐标系下的位置矢量与质心速度

这里将驱动臂分成电动推杆和电动缸两部分来考虑:设置参数，电动缸的长度为lx，电动推杆的长度为ls，且质量分别为mx和ms，电动缸质心到根部铰链距离为lex，电动推杆质心到顶部铰链距离为les。

电动缸质心位置矢量

电动推杆质心位置矢量

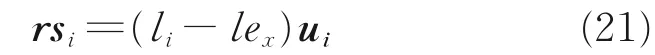
电动缸质心速度

电动推杆质心速度

2 动力学模型建立

动力学方程采用拉格朗日求解，空间先不考虑势能，需要求解LIDM 的动能和广义惯性力，把对接机构分解为2 个子系统来分别考虑，即负载传感环和6 根驱动臂。首先在基坐标系下，推导这两个子系统的动能，推导广义惯性力，然后来推导整体的动力学方程。

2.1 负载传感环的动能与势能

根据式(13)可知负载传感环的空间运动角速度为ω0，则负载传感环的平动和转动的机构动能K0为

式中：m0为负载传感环的质量；p 为负载环质心在基坐标下的位置矢量；I0为负载传感环相对于{a}的转动惯性张量；ω0为负载传感环相对于基坐标系{A}下的角速度。

将式(13)代入式(24)并处理矩阵关系，简化过程略，直接给出关系式如下

式中M 为一个6×6 的矩阵

负载传感环势能表达式非常简单，即

2.2 负载传感环的动能与势能

这里将驱动臂分成电动推杆和电动缸两部分来考虑:设置参数，电动缸的长度为lx，电动推杆的长度为ls，缸体、杆的质量分别为md和ms。将它们看成具有各自转动惯性张量矩阵的刚体。为了计算其动能相应在基坐标系下的表达，参考1.2 节的姿态描述所得出各根驱动臂的方向余弦矩阵Ti。电动推杆与电动缸的惯性张量一般在自身坐标系进行描述,并令第i 根杆的电动推杆与电动缸惯性张量分别为I1i和I2i（自身坐标系），则电动推杆与电动缸的惯性张量在旋转后的自身固定坐标系下的表达如下

动能计算中将动参考点选到质心位置，消除平移与转动的耦合项。动能看成质量集中于质心的质点动能和绕质心转动动能的简单叠加。

电动推杆动能

电动缸动能

电动推杆与电动缸的势能依据式(20)与式(21)可得到

2.3 LIDM 捕获过程中的广义惯性力

作用在LIDM 上的主动力主要影响因素包括驱动臂的驱动力与负载环碰撞产生的接触力。鉴于LIDM 的负载传感环上安装有六维力传感器，碰撞接触力等均等效为作用在负载环环心的合力。这包含了力与力矩两个部分[13]。

设位姿信息q= [ x y z α β γ ]T。

取位姿信息为广义坐标。广义力是作用于广义坐标上的力。为了计算广义力，通过计算系统内全部主动力的虚功，然后将所有的虚位移用广义坐标的变分表示，各个广义坐标变分前的系数即为相应的广义力[12]。设驱动臂关节驱动力为

同时设其余等效合力为

在δt 时间内，设驱动臂关节虚位移量为

系统虚功如下

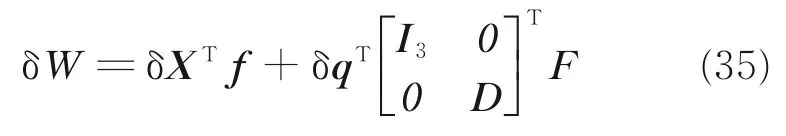
驱动臂关节变分δX 与δq 存在如下关系

式中J 被称为速度雅克比矩阵。将式(36)代入式(35)，可以得出广义力表达式

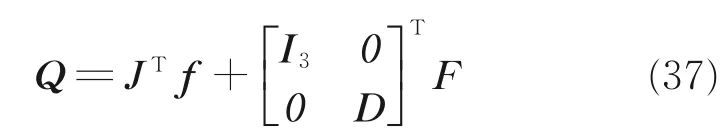
2.4 LIDM 的动力学方程

拉格朗日方程是确定质点系运动规律的普遍形式动力学方程，可以用来建立不含约束力的动力学方程，也可以用来在给定系统运动规律的情况下求解作用在系统上的主动力。

根据LIDM 所处的外在环境，不考虑对接机构接触元件的微小变形，故系统拉格朗日方程如下

只需要计算系统的动能、势能以及广义力即可应用拉格朗日方程。

总动能

总势能

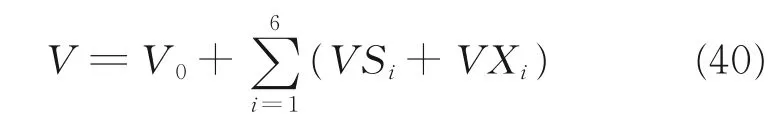
拉格朗日函数

将式(37)和(41)代入式(38)即可以得到动力学方程，限于篇幅，这里不给出其具体的显示表达式。

3 仿真算例及结果分析

3.1 仿真结果

本节将在已知对接环LSR 位姿的条件下，对各个驱动臂产生相应运动时所输出的驱动力进行仿真验证。按照以上算法，利用MATLAB 编制程序对系统的动力学进行计算，并利用商业软件AD⁃AMS 进行仿真对比验证。

弱撞击对接机构的各项参数设置如表1～4 所示。其中表2 动力学参数参考建模过程，为自身坐标系下的数值。

表1 弱撞击对接机构的基础构型参数Table 1 Basic configuration parameters of LIDM

表2 系统动力学参数Table 2 System dynamics parameters

表3 驱动臂的控制特性参数Table 3 Control characteristic parameters of driving arm

表4 负载环的参数设置Table 4 Parameter setting of load ring

给予负载环沿Z 轴z=0.1×sin(πt/5)m 的升降运动规律。重力加速度大小g 取0 m/s2。

根据MATLAB 构建的动力学模型，各驱动臂驱动力大小计算结果如图5 所示。

图5 各驱动臂的驱动力大小Fig.5 Driving force of each driving arm

下面通过ADAMS 软件对上述的LIDM 捕获动力学模型进行仿真运算来验证以拉格朗日方程建立的动力学模型。首先根据LIDM 的质量、几何结构组成、运动学参数、受力状态等在ADAMS 内构建虚拟样机，设置合理的约束并以直线驱动施加给每根驱动臂。ADAMS 虚拟样机如图6 所示。

图6 ADAMS 虚拟样机Fig.6 ADAMS virtual prototype

LIDM 通过改变驱动臂的伸缩量来改变LSR对接环的位姿，为了模拟这一过程，事先在MAT⁃LAB 中通过运动学反解来求解出在上述LSR 对接环运动规律下的各驱动臂工作行程。由于该运动规律定位升降运动，且初始姿态角均为0、系统几何结构具有对称性，故6 根驱动臂工作行程一致，如图7 所示。可见工作行程满足表3 的控制特性。

在ADAMS 中将上述图7 中曲线以样条曲线的形式作为输入量、以位移类型作为ADAMS 中驱动的输入，并施加与MATLAB 程序中相同方向的外力，进行ADAMS 的仿真运算，输出相应的驱动力曲线如图8 所示。

图7 各驱动臂的工作行程Fig.7 Working stroke of each driving arm

图8 各驱动臂的驱动力大小Fig.8 Driving force of each driving arm

为了更加形象直观，导出图8 中各曲线数值，并将每根驱动臂的MATLAB 理论值与ADAMS仿真值放在一张图中进行对比。对比图如图9所示。

图9 一般外力工况下驱动臂验证结果对比Fig.9 Comparison of verification results of driving arm under general external force conditions

仅改变负载环质心所受的外力作用力[F FM]T=[0 0 0 100 200 0]T，由原先的一般外力工况变更为外力矩工况。依照相同方法求得程序与仿真对比结果如图10 所示。

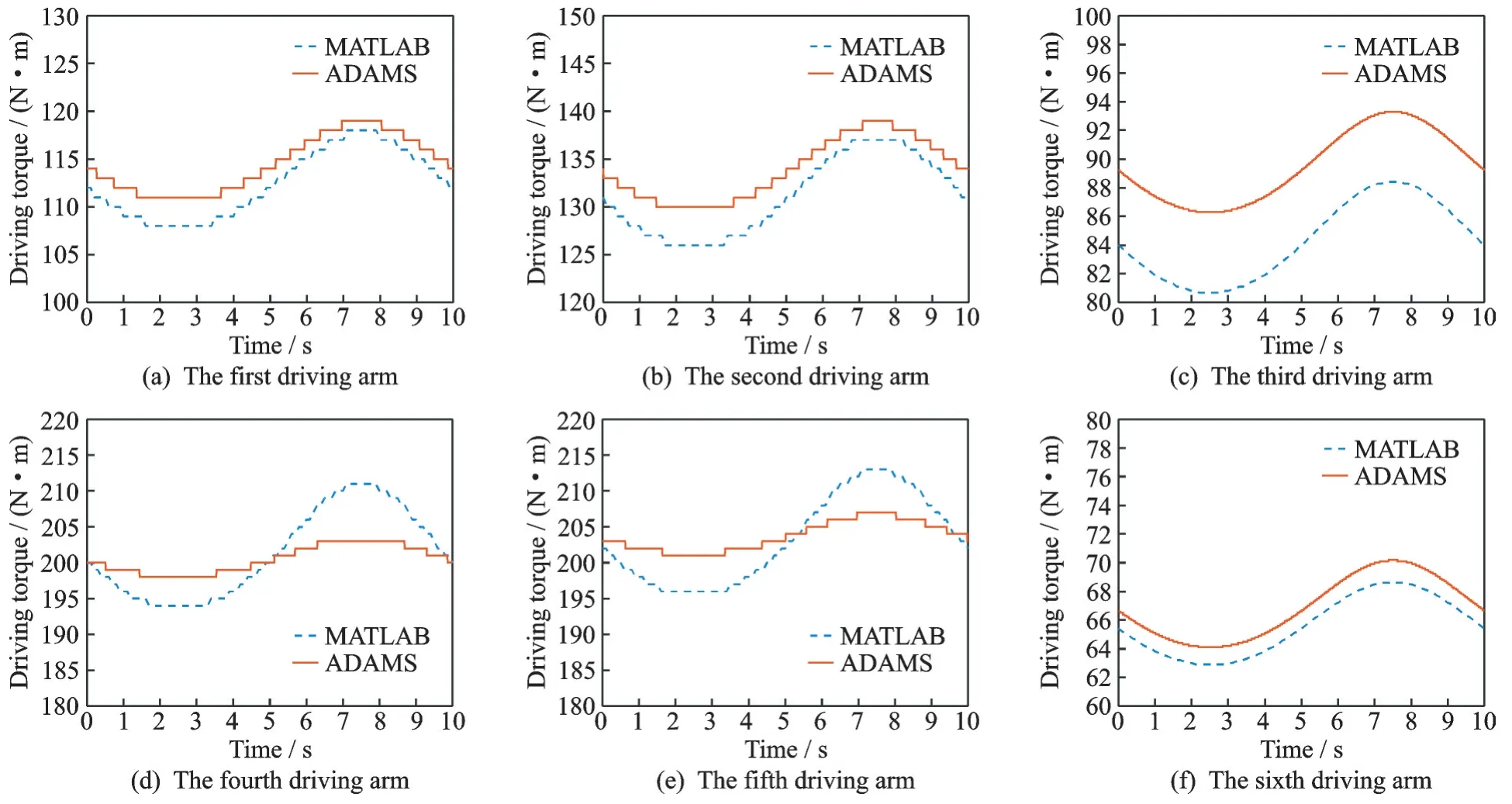
图10 一般外力矩工况下驱动臂验证结果对比Fig.10 Comparison of verification results of driving arm under general external torque conditions

3.2 结果分析

图9 与图10 给出了在已知对接环LSR 位姿的条件下，给对接环施加不同方向的作用力/力矩，两种工况下各个驱动臂所输出的驱动力的仿真验证对比图。从图中可见，ADAMS 仿真结果趋近MATLAB 的理论值，这里考虑到理论模型与仿真模型之间存在有铰链空间、样条曲线的插值转化等不可避免的误差情况，如果忽略这些因素，两者的计算结果基本一致。由此得出，ADAMS 的仿真结果验证了由拉格朗日方程建立的LIDM 捕获动力学模型的正确性，捕获动力学的建立为控制算法的搭建与优化算法的进程提供了数字模型。

4 结 论

本文研究了弱撞击对接机构在捕获阶段的动力学建模方案。通过将外部载荷简化为LSR 对接环质心，以LSR 随体坐标系相对基坐标系的位姿作为广义坐标，利用拉格朗日方程建立了系统的捕获动力学方程，方程构成形式简洁，易于求解。此外，通过MATLAB 计算出相关的动力学参数，同步建立了ADAMS 仿真模型，验证了模型的正确性。驱动力的计算分析研究对于弱撞击对接机构本体的机械结构、控制系统研发优化等工作提供理论与数据支持。但本文视各铰链为理想铰链，未考虑铰链间隙、关节摩擦等带来的影响。因此后续研究将考虑关节间隙、精度、结构优化等问题的求解。