群孔齐发爆破岩体振动频谱特性研究*
2021-03-31李新平张雪屏刘飞香郑博闻
李新平,张雪屏,刘飞香,郑博闻,罗 忆
(1.武汉理工大学 a.道路桥梁与结构工程湖北省重点实验室;b.土木工程与建筑学院,武汉 430070;2.中国铁建重工集团有限公司,长沙 410100)
钻孔爆破是目前岩体开挖过程中应用最广泛且高效的手段。由于爆炸冲击作用力巨大,且仅有20%左右的能量被用于破碎岩体,更多的能量以振动波的形式向周围岩体传播,从而会对周边结构带来诸多不良影响[1]。爆破振动的幅值和频率都随时间而变化,以往的研究主要通过质点峰值振动速度来调整岩体爆破开挖参数,而新修订的《爆破安全规程》(GB6722—2014)[2]提出将质点峰值振动速度和主振频率作为爆破振动的联合安全判据,使得爆破振动的频谱特性获得了更多的关注和研究[3]。
目前,国内外学者在爆破振动频谱响应特性方面已经取得了一定的成果。Kjartansson将爆破振动幅值转化到频域上,获得了爆破振动波形的变化规律[4]。张继春等采用频域统计的方法分析了三峡工程中现场爆破的实测数据,发现质点振动主频与爆心距及药量之间均成反比关系[5]。孟海利等通过对现场试验得到的爆破振动主频特征及其影响因素进行研究,推导出特定爆破条件下主频的预测公式[6]。李鹏等运用理论分析推导了三角形爆炸荷载的频域表达式以及球状药包、长柱状药包爆炸诱发振动的频域解析解,并基于爆炸荷载等效模拟分析了单孔爆破诱发振动的主频衰减规律[7]。饶宇等通过现场试验对预裂孔和主爆孔的振动信号进行分析,研究了预裂缝对爆破振动频谱特征变化的影响[8]。
岩体爆破开挖激发的振动不可避免地会对周围岩体造成一定程度的损伤[9]。为了充分发挥爆破器材的作用效率,实际岩体开挖工程中更倾向于采用多孔多段爆破。但目前针对群孔起爆激发爆破振动频率衰减规律及其影响因素的研究,大多采用理论分析方法对单个炮孔的爆破信号进行叠加,由此得到相应的爆破振动规律,而对于群孔爆破振动频谱特性的相关理论研究较少[10-13]。
以露天深孔台阶爆破为研究对象,探讨正方形布孔形式下群孔齐发起爆时的岩体振动频谱特性及其影响因素。
1 群孔等效弹性边界及爆炸荷载峰值
1.1 群孔等效弹性边界
岩体爆破开挖完成后,可将炮孔周围岩体的破坏程度依次划分为粉碎区、破碎区和弹性振动区,如图1所示。其中rb,rc和rf分别为炮孔、粉碎区和破碎区的半径。常规炸药引起的粉碎区半径rc约为装药半径的3~5倍,破碎区半径rf约为装药半径的10~15倍[14]。
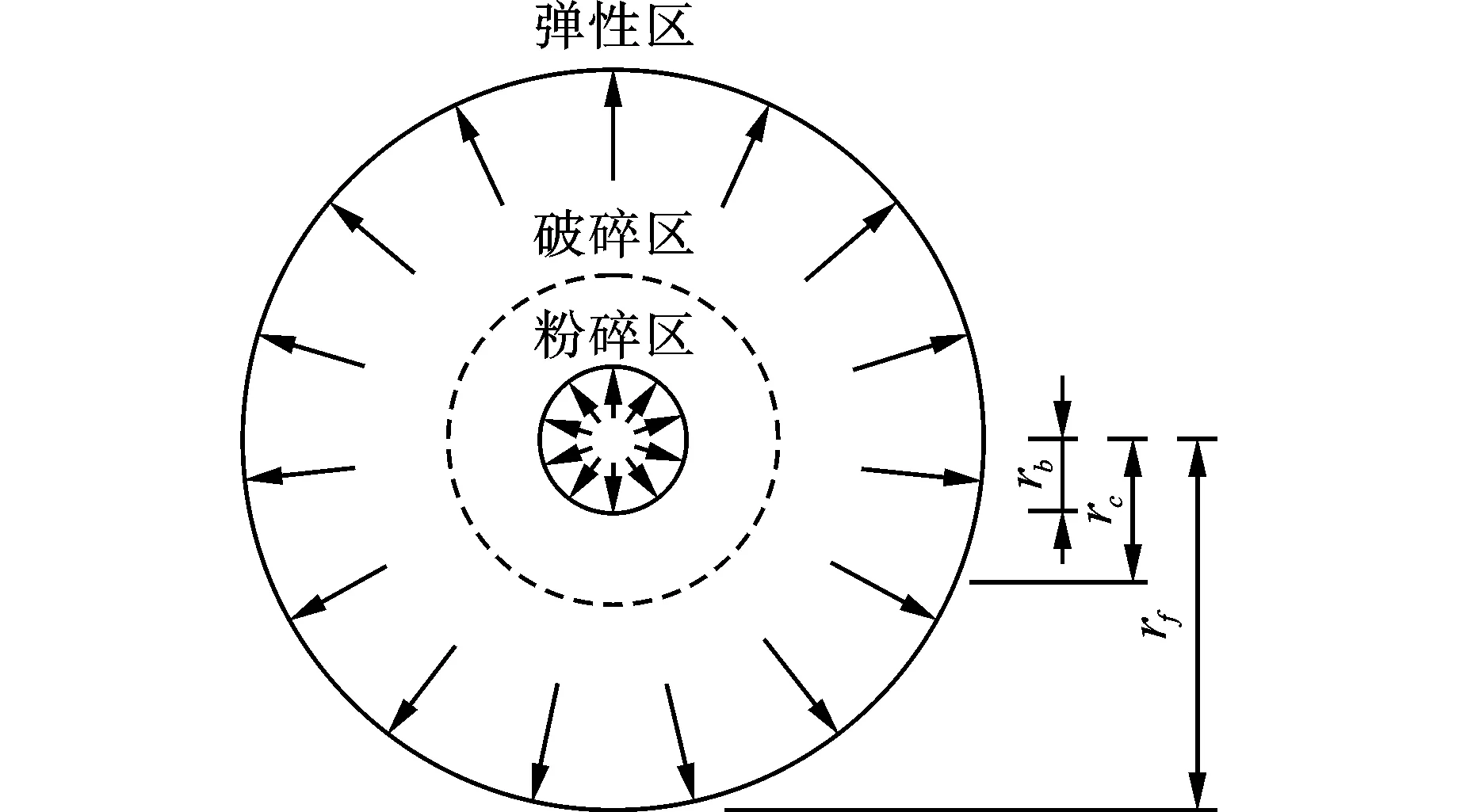
图 1 爆炸破坏分区Fig. 1 Explosion damage partition
由于群孔起爆激发的不同应力波波阵面传播至岩体中某一位置的时间远小于荷载作用时间,一般可以忽略各炮孔之间的相互影响,认为各孔爆破激发的应力波波阵面同时到达此位置。因此,每一个炮孔均可认为是柱状炸药在半无限介质中起爆,各孔起爆后所形成的破碎区的包络线是群孔起爆的等效弹性边界[15],如图2所示。

图 2 群孔起爆等效弹性边界示意图Fig. 2 Schematic diagram of equivalent elastic boundary for group hole initiation
1.2 群孔等效爆炸荷载峰值
考虑到等效弹性边界形状的不规则性,其半径很难用公式直接计算。采用等代圆的方法,将等效弹性边界所包含的岩体,等效为面积相等的圆,则其等效半径就可以按照相应的等效圆的面积进行计算[16]
(1)
基于上述理论,王先前等推导出群孔爆破时的等效爆炸荷载峰值为[17]
(2)
式中:k为群孔起爆时的影响系数;P0为耦合装药下单孔爆炸荷载峰值;ν为泊松比。
其中,k值与炮孔的数量和分布形式有关,主要考虑各孔爆破产生的应力波在等效边界处的叠加效应,按下式计算[16]
(3)
式中:n为炮孔数量。
根据不耦合装药与耦合装药下最大爆轰压力的关系,引入不耦合装药影响系数β,则不耦合装药条件下群孔爆破时的等效爆炸荷载峰值可表示为
P′b=βPb
(4)
其中,β按下式计算[18]
(5)
式中:ra为装药半径;rb为炮孔半径;s为装药系数,集中装药和球状装药时s均取3,柱状装药取2;z为爆生气体等熵绝热指数,一般取3。
2 群孔等效爆炸荷载的频域解
群孔爆炸荷载可由单孔爆炸荷载叠加得到,假定各孔起爆时间相同,且不考虑各孔爆炸冲击波到达测点的时间差,结合群孔等效爆炸荷载峰值公式(2)与震源荷载函数曲线(图3),可以得到群孔爆炸荷载频谱曲线。国内学者大多采用三角形爆炸荷载函数曲线进行研究[19-21],该过程主要表现为超压达到峰值以后便迅速衰减。

图 3 三角形爆炸荷载曲线Fig. 3 Triangular blast load curve
三角形爆炸荷载函数曲线如图3所示,其时域表达式为[7]
(6)
式中:Pb为群孔爆炸荷载峰值;tr,tD分别为荷载上升时间及荷载下降时间。
将上述时域表达式通过傅里叶变换,并结合公式(2)可以得到群孔爆炸荷载的幅值谱为
(7)
式中:ae=tR/t,be=tD/t。
由式(7)可以看出,影响爆炸荷载频谱的参量主要为荷载上升时间tr及荷载下降时间tD。
通常将爆轰波在炮孔内传播时间作为爆炸荷载上升时间[7],其计算表达式为
(8)
式中:L1为炮孔的装药段长度;D为炸药的爆轰速度。
爆炸荷载作用的持续时间为炸药起爆后炮孔间裂缝贯通,爆生气体逸出,直至炮孔压力下降到大气压所需要的时间,爆炸荷载持续时间可以表示为[21]
(9)
式中:h为相邻两炮孔间距;L2为炮孔的堵塞段长度;cf为爆炸荷载驱动下的裂缝扩张平均速度;ca为爆生气体的卸载波速度;cb为从孔底往孔口方向传播的反射卸载波速度;va为爆生气体的逸出速度。
对于露天深孔台阶爆破,当炮孔的钻孔直径d=30~150 mm,炮孔间距h=0.8~5.0 m,台阶高度为8~15 m时,由公式(8)及公式(9)可估算出爆炸荷载的上升时间为0.5~4 ms,持续时间为5~100 ms。取三角形荷载的持续时间为10 ms,上升时间tr分别为0.5 ms、1 ms、2 ms时,采用公式(7)可以计算得到如图4所示的爆炸荷载频谱曲线。为了便于比较频率衰减规律,将频率幅值进行归一化处理,即将不同频率的幅值与最大幅值的比值作为纵坐标。由图4可知,爆炸荷载频谱幅值随频率的增加而逐渐衰减,并伴有波动现象。随着荷载上升时间的增加,频谱幅值衰减得更快,即高频成分减少,低频成分所占的比例增大。
取三角形荷载的上升时间为1 ms,下降时间分别为4 ms、6 ms、10 ms,爆炸荷载的归一化幅值谱如图5所示,可以看出,随着爆炸荷载下降时间的增加,高频成分逐渐衰减,低频成分所占的比例逐渐增大。爆炸荷载的上升和下降时间均对频谱成分比例产生影响,荷载上升或下降时间越长,能量越向低频集中。

图 4 不同上升时间的爆炸荷载频谱曲线Fig. 4 Spectrum curve of explosion load with different rise times
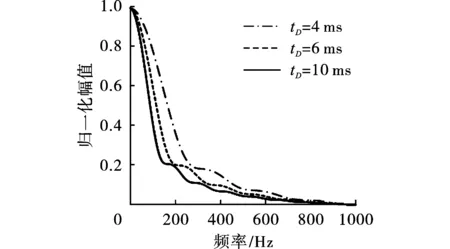
图 5 不同下降时间的爆炸荷载频谱曲线Fig. 5 Spectrum curve of explosion load with different duration
3 群孔齐发爆破岩体振动频谱特性
3.1 群孔齐发起爆激发岩体振动速度幅值谱
群孔爆破其实是多个单孔在不同时空下的组合爆破,当单孔爆破和群孔爆破地震波传播的地质条件完全相同时,理论上,将爆破振动叠加过程假设为一个线性系统是可行的[22]。因此,可基于弹性岩体爆破振动理论解,进行不同影响因素下群孔起爆激发爆破振动频率衰减规律的研究。
卢文波等在球形空腔激发的弹性波理论解中[23],引入介质阻尼项,得到黏性岩体中爆破振动速度幅值谱为
(10)

式中:λ,μ为拉梅系数;CP为纵波速度;Qr为岩石地质品质因子;re为群孔等效弹性空腔半径;AP(ω)为群孔等效弹性空腔内荷载幅值谱;ω为角频率;r为爆心距。
从式(10)中可以看出,荷载幅值谱AP(ω)直接影响速度幅值谱Fn(ω),因此,爆炸荷载上升及下降时间也是爆破振动速度幅值谱的影响因素。将荷载幅值谱表达式(7)带入式(10),得到群孔齐发爆破时的振动速度幅值谱表达式为
(11)
由式(11)可知,群孔齐发起爆激发岩体振动速度谱的影响因素主要有:爆心距r;等效弹性边界半径re;爆炸荷载作用参数tr、tD;岩石参数λ、μ、CP和Qr。
3.2 群孔齐发起爆激发岩体振动频率衰减规律
采用群孔齐发爆破时的振动速度幅值谱表达式(11)对正方形布置的四孔齐发起爆模型进行计算,分析不同影响因素下群孔爆破振动频谱的变化规律。计算时仅考虑群孔齐发爆破的情况,并假定各爆孔半径、装药长度及装药量相同,炮孔直径d=42 mm,岩石参数为Qr=12,λ=30 GPa,μ=13.5 GPa,CP=4600 m/s,ν=0.22,爆炸荷载参数tr=2 ms,tD=8 ms,P0=460 MPa。
在相邻炮孔间距h=0.8 m,等效弹性边界半径为re=1.3 m的条件下,得到不同爆心距处的爆破振动频谱曲线,如图6所示,可以看出,频谱曲线总体呈现出以主频为对称轴的三峰结构,爆心距越大,高频成分衰减越快,爆破振动主频逐渐向低频偏移,频谱曲线由多峰结构逐渐衰减为主频位于低频带的单峰结构。频谱曲线结构随着爆心距增大时,中部主频幅值逐渐降低,低频带第二主频逐渐增大。下面以爆破振动主频随爆心距衰减曲线来进一步分析,如图7所示,爆破振动主频随爆心距增大而减小,在爆心距为110 m处主频值衰减到与第二主频相同,主频衰减速度增大,从而导致主频随爆心距衰减的曲线不连续。
在爆心距r=50 m,炮孔间距h不同的条件下,得到不同炮孔间距时的爆破振动频谱曲线,如图8所示,当炮孔间距h较小时,爆破振动频谱结构呈现出以主频为对称轴的三峰结构,随炮孔间距增大,爆破振动主频由高频向低频衰减,频谱曲线由多峰结构逐渐衰减为近似单峰结构,即高频所占比例逐渐减小。下面以爆破振动主频随炮孔间距的衰减曲线来进一步分析,如图9所示。在同一爆心距处,爆破振动主频随炮孔间距h的增大而发生衰减,在炮孔间距为3 m时主频值衰减到与第二主频相同,主频衰减速度增大,从而导致主频随爆心距衰减的曲线不连续。

图 6 不同爆心距的爆破振动频谱曲线Fig. 6 Blasting vibration spectrum curve with different blasting distances
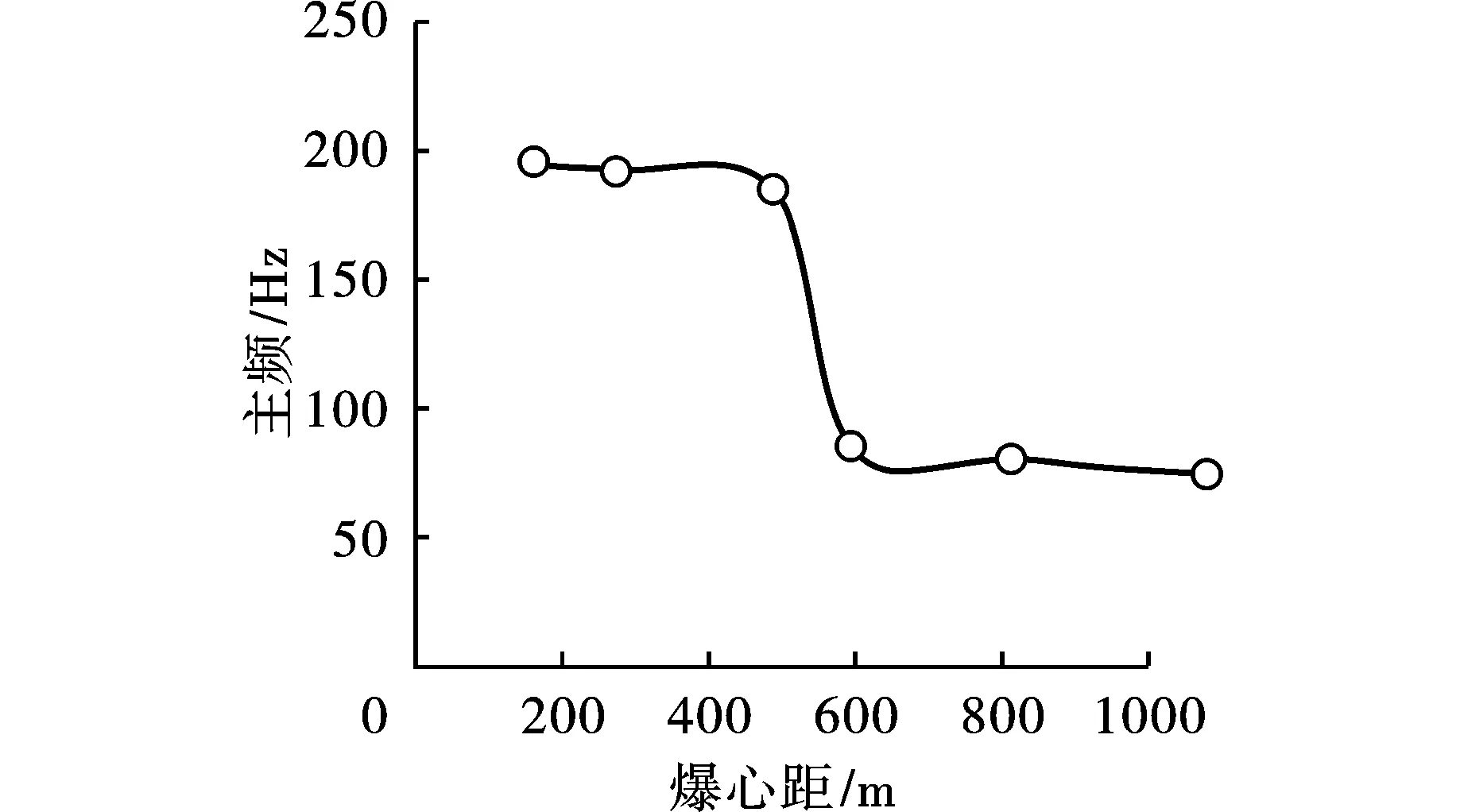
图 7 爆破振动主频随爆心距衰减曲线Fig. 7 Blasting vibration frequency attenuation curve with blasting center distance change
在爆心距r=50 m,炮孔间距h=0.8 m,单孔药量Q不同的条件下,群孔爆破振动频谱曲线如图10所示。在同一爆心距处,爆破振动主频随单孔药量Q的增大变化幅度较小,主频基本维持在200 Hz左右。随单孔药量Q的增大,爆破振动频率由高频小幅度地向低频衰减,高频成分逐渐减少,低频成分逐渐增多。

图 8 不同炮孔间距的爆破振动频谱曲线Fig. 8 Blasting vibration spectrum curve with different hole spacing

图 9 爆破振动主频随炮孔间距衰减曲线Fig. 9 The main frequency of blasting vibration with the blasthole spacing attenuation curve
选取溪洛渡水电站尾水洞的玄武岩、瀑布沟水电站引水洞的花岗岩、锦屏二级水电站引水洞的大理岩作为研究对象,这三种典型岩体参数如表1所示。

表 1 典型爆破开挖工程的岩体参数Table 1 Rock mass parameters of typical blasting excavation engineering
在炸药参数及炮孔布置形式不变的情况下,计算三种实际工程岩体的爆破振动主频衰减曲线,如图11所示,三种岩体参数下爆破振动主频均随爆心距的增大而发生衰减,但主频的衰减速度不同。主频与弹性模量及纵波波速成正比,而主频衰减速度与弹性模量及纵波波速成反比,其中锦屏大理岩的爆破振动主频最小,且主频衰减速度最快。

图 10 不同单孔药量的爆破振动频谱曲线Fig. 10 Blasting vibration spectrum curve with different single hole charge

图 11 不同岩体参数下爆破振动主频随爆心距衰减曲线Fig. 11 Blasting vibration frequency attenuation curve with blasting center distance under different rock mass parameters
由上述对不同影响因素下群孔爆破振动频谱变化规律的分析可知,爆心距r、炮孔间距h、单孔药量Q均对爆破振动频谱结构有一定的影响。随着这三个因素对应的值增大,频谱曲线均呈现高频成分减小而低频成分增加的现象。其中,随爆心距r或炮孔间距h的增大,爆破振动主频均呈现出明显的衰减,由于频谱曲线为多峰结构,在某一爆心距r或炮孔间距h处主频由中部频带第一主频跃迁至低频带第二主频,从而导致主频随爆心距r或炮孔间距h衰减的曲线不连续。在不同参数的岩体中进行群孔齐发爆破时,爆破振动主频随着岩体弹性模量及纵波波速的增大而增大,但主频衰减速度随爆心距的增大而减小。
4 结论
通过群孔齐发爆破振动频谱分析方法,从爆源因素出发,对露天深孔台阶爆破的四孔正方形布置的炮孔起爆进行了研究,推导出群孔齐发爆破振动频谱表达式,并对不同影响因素下频率的衰减规律进行了分析:
(1)群孔齐发起爆激发的岩体振动速度幅值谱与爆心距、孔间距、弹性区边界半径、爆破荷载作用参数、岩石参数等因素相关,其中爆炸荷载的上升时间及下降时间直接影响爆破振动频谱的成分比例。
(2)随爆心距、孔间距、单孔药量的增大,频谱曲线呈现高频成分减小和低频成分增加的现象。其中,随爆心距或炮孔间距的增大,爆破振动主频的衰减现象更明显。
(3)不同岩体参数条件下,主频与弹性模量及纵波波速成正比,而主频衰减速度与弹性模量及纵波波速成反比。相比于溪洛渡玄武岩及瀑布沟花岗岩,锦屏大理岩爆破激发的振动频率最小,且主频衰减速度最快。
对于其他爆破布孔形式,以及台阶爆破中的多排多段叠加和延时间隔起爆对爆破振动频谱的影响,还有待进一步研究。
