基于Nastran农用EV80型二缸柴油机曲轴性能分析*

郭俊，杨国伟，沈文龙，刘玮

(1. 盐城工学院汽车工程学院，江苏盐城，224051； 2. 南京理工大学机械工程学院，南京市，210094； 3. 南京农业大学工学院，农业智能化装备实验室，南京市，210031)

0 引言

目前，现代结构分析中，应用比较广泛的有：结构力学和固体力学[1-2]。两者对于一般问题的分析可以通用，但针对特殊复杂的问题，两种分析方法局限性较强。如今，伴随着计算机的发展，有限元法已成为结构分析中强有力的数据分析方法，有限元法与工业软件相结合应用的范围越来越广，并形成了一种新的学科—计算力学[3-5]。有限元法为曲轴的分析提供了可靠理论依据[6-7]。发动机中包含的零部件有：机体、缸盖、活塞、连杆、曲轴等。各零部件都可以通过相关软件完成建模和分析，如西门子开发的NX软件等[8]。

曲轴作为柴油机里重要和复杂的部件，同时也是极易损坏的部件。它的刚度和强度会直接影响发动机的性能。运行过程中，曲轴既承受着缸内的气体压力和往复旋转惯性力引起的周期性变化的载荷，同时还会承受弯曲、扭转时产生的振动等[9-10]。由于曲轴在工作过程中受到复杂的应力作用，以及曲轴形状的复杂性，曲轴颈和连杆轴颈结构相互交错，于是在连接体圆角区域极易产生应力集中[11-12]。当柴油机长时间工作，曲轴的寿命难以得到保障且容易发生故障。故障主要表现为：曲轴疲劳产生的裂纹、磨损等[13-17]。随着发动机工况不断的强化，尤其农业机械[18-19]，其工作环境及其恶劣，于是对曲轴的工作性能提出了更高的要求。

综上所述，对曲轴前、后端以及整体结构的分析和设计[20]，如何在交变载荷的作用下准确得到曲轴变形的应力大小以及应力分布情况显得尤为重要，通过计算机模拟仿真得到的理论结果可为曲轴的优化和改进提供计算依据，并有效校核曲轴的疲劳强度，从而提高发动机使用寿命。

1 曲轴的静力分析

1.1 曲轴几何模型的建立

本文以EV80型2缸柴油机曲轴作为研究对象。曲轴模型的总长为392.5 mm，主轴颈直径为80 mm，连杆轴颈的直径为66 mm，曲轴整体为全支承式。曲轴的几何模型，如图1所示。

图1 曲轴的几何模型Fig. 1 Geometric model of crankshaft

1.2 运动工况分析及载荷求解

2缸4冲程发动机点火顺序为1～2，各缸分布如图2所示。气缸做功时受到最高的爆发压力，此时曲轴的应力和变形最大，此时曲轴的破坏主要为弯曲变形，忽略扭矩载荷作用。当一缸点火时，活塞向下做直线运动，连杆轴颈到达下止点，此时，二缸的连杆轴颈就会到达上止点，处于压缩状态，且应力载荷达到最大值。所以只需要在二缸点火时，考虑活塞处于上止点时连杆轴颈受力。

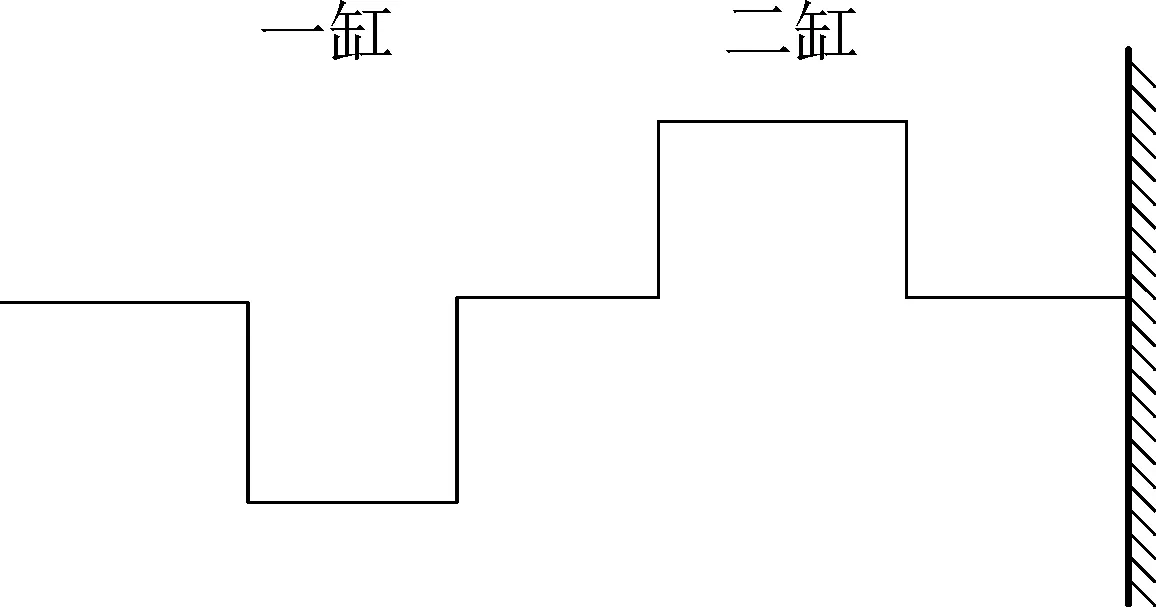
图2 各缸分布Fig. 2 Distribution of each cylinder

由于柴油机的两缸曲柄之间相差180°，只需求出任意一缸在0°、180°、360°、540°、720°的载荷即可。结合图2和发动机的发火顺序，就二缸而言，在0°～720°内随转角变化的曲柄连杆结构示意图如图3所示。图3中r为曲柄半径；l为连杆半径；λ为曲柄连杆比；α为曲柄转角；β为连杆摆角。

图3 曲柄连杆结构Fig. 3 Structure of crank connecting rod

1) 活塞在往复运动时沿连杆方向的分力

(1)

式中：λ——曲柄半径r和连杆半径l的比值，即r/l；

∑mj——活塞销中点处往复运动的质量。

活塞销的中点质量设为1.5 kg，活塞转速为2 000 r/min ≈200 rad/s，连杆长度l为200 mm，曲柄半径r为50 mm，缸径为150 mm，曲柄连杆比λ=50/200=0.25,得出活塞分力随曲轴转角的值，如表1所示。

表1 活塞分力与曲轴转角变化值Tab. 1 Component force of piston and change value of crankshaft angle

2) 气体对活塞的作用力。气缸内气体压强[21]如表2所示。

表2 气体压强随曲轴转角变化值

F气=(Pg-Po)×(π/4)D2/cosβ

(2)

β=arcsin(λsinα)

(3)

式中：D——缸径；

Pg——缸内气体的绝对气压；

Po——曲轴箱内的绝对气压，取0.1 MPa[21]。

结合以上所有数据，得到一组随曲轴转角变化的气体压力值，如表3所示。

表3 气体作用力随曲轴转角变化值

3) 连杆在曲轴上的惯性力，计算如式(4)所示。

F惯=mrw2=1.5×0.05×40 000=3000 N

(4)

式中：m——按静力等效的连杆质量。

4)Fa为活塞和气体在沿曲柄的方向上的作用力，Ft是沿连杆在曲柄方向上的法向作用力，活塞所受力为两者的矢量和，即：F活塞=Ft+Fa。如图4所示。

图4 连杆轴颈受力Fig. 4 Force on connecting rod journal

Fa=F惯+(-F气+F活塞)×cos(α+β)

(5)

Ft=(-F气+F活塞)×sin(α+β)

(6)

得到Fa及Ft随着曲轴转角的变化而变化的值。第一连杆轴颈为18 678.75 N，第二连杆轴颈为11 613.75 N，如表4所示。

表4 Fa及Ft随着曲轴转角变化值

1.3 曲轴分析及边界条件的施加

1.3.1 材料属性定义

在本文中材料为40CrMo，弹性模量E=2.07×105MPa，密度ρ=7.9×10-6kg/mm3，泊松比μ=0.3，强度极限σ=938 MPa。

在连杆轴颈和主轴颈处考虑到弯曲和变形，利用四面体网格把模型一共划分为189 584个单元和300 829 个节点。曲轴的网格划分模型如图5所示。

图5 曲轴网格模型Fig. 5 Mesh model of crankshaft

1.3.2 边界条件确定

曲轴的边界条件分为两大类：一类是力边界条件，另一类是边界约束条件。首先，第一类是力边界条件，它由连杆施加的推力，飞轮传递的扭矩，曲轴自身旋转产生的离心力和自身的重力。对于每一个主轴颈，其只能沿着轴线转动。所以对于主轴颈限制其径向方向的自由度即可。对于曲轴与飞轮相连接的一端，要限制其XYZ方向的自由度。对于曲轴自由端，应该限制其轴向位移。把载荷和边界条件一起添加到曲轴中，如图6所示，G代表曲轴的重力，q代表曲轴旋转的离心力。A代表连杆轴颈所受到的载荷；B代表限制主轴颈径向的自由度；C代表主轴端限制转动的自由度；D代表自由端六个自由度全约束。

图6 边界条件和载荷分布Fig. 6 Boundary conditions and load distribution

1.4 位移变形分析

1.4.1 缸点火工况结果分析

1) 曲轴的一缸点火工况下，测得曲轴最大的变形量为0.089 5 mm。最大变形量位于曲轴第一连杆轴颈左端曲柄臂的平衡块尾部，如图7所示。对于X轴方向，从自由端向主轴端观察，最大的位移点位于第二连杆轴颈的左侧，变形量为0.001 2 mm，如图8所示。

图7 曲轴整体变形Fig. 7 Overall deformation of crankshaft

图8 曲轴X方向变形Fig. 8 Crankshaft deformation in X direction

2) 对于Y轴方向，最大的位移点与幅值的方向极为相似，位于第一连杆轴颈左端的曲柄臂平衡块尾部。变形量是0.024 mm，如图9所示。对于Z轴方向，最大的位移点处于第一连杆轴颈在Z轴正方向的中央位置。最大的变形量为0.088 4 mm，如图10所示。

图9 曲轴Y方向的变形Fig. 9 Crankshaft deformation in Y direction

图10 曲轴Z方向变形Fig. 10 Crankshaft deformation in Z direction

综上所述，曲轴位移整体变化趋势与Z轴方向变化趋势相同，且变形量接近。根据曲轴的许可挠度的计算准则:[y]=0.000 4L，L为两端支承的直线距离。由上文的数据可得L为394 mm。代入公式得出：[y]=0.157 mm。本曲轴的最大挠度为0.089 5 mm 远小于0.157 mm，所以结合以上数据，可以得出曲轴的刚度是符合实际工况的要求的。

3) 在一缸点火的情况下，在第一、二连杆轴颈上均有载荷。因此在对曲轴进行整体计算时，需要把这两个轴颈的载荷都要考虑进去。应力图如图11所示，曲轴等效应力的最大值在第二连杆轴颈右边的平衡块与右主轴颈的接缝处，位于Z方向上方处，数值为246.55 MPa。

图11 一缸点火工况下等效应力Fig. 11 Equivalent stress of cylinder 1 ignition

1.4.2 缸点火工况结果分析

1) 曲轴的二缸点火工况下，测得曲轴最大的变形量为0.020 7 mm。位置处于曲轴第一连杆轴颈左端曲柄臂的平衡块尾部，如图12所示。对于X轴方向，从自由端向主轴观察，最大的位移点位于第二连杆轴颈的左侧上部，变形量为0.000 4 mm，如图13所示。

图12 曲轴整体变形Fig. 12 Overall deformation of crankshaft

图13 曲轴X方向变形Fig. 13 Crankshaft deformation in X direction

2) 对于Y轴方向，最大的位移点与幅值的方向相同，位于第二连杆轴颈左端的曲柄臂平衡块顶部与轴颈相连的位置。变形量是0.011 7 mm，如图14所示。对于Z轴方向，最大的位移点处于曲轴第一连杆轴颈左侧的曲柄臂的Z轴负方向的圆角处，最大的变形量为0.020 7 mm，如图15所示。

图14 曲轴Y方向的变形Fig. 14 Crankshaft deformation in Y direction

综上所述，曲轴整体变化位移量与Z轴方向位移量相同。根据曲轴的许可挠度的计算准则:[y]=0.000 4L，L为两端支承的直线距离。由上文的数据可得L为394 mm。代入公式得出：[y]=0.157 mm。本曲轴的最大挠度为0.020 7 mm远小于0.157 mm，所以结合以上数据，可以得出曲轴的刚度是符合实际工况的要求的。

图15 曲轴Z方向变形Fig. 15 Crankshaft deformation in Z direction

3) 在二缸点火的情况下，在对曲轴进行整体计算时，同样需要考虑两个轴颈的载荷。应力图如图16所示，曲轴等效应力的最大值在第二连杆轴颈右边的平衡块与右主轴颈的接缝处，位于Z方向上方处，数值为73.37 MPa。

图16 二缸点火工况下等效应力Fig. 16 Equivalent stress of cylinder 2 ignition

2 疲劳强度分析

2.1 曲轴的疲劳强度

曲轴的失效疲劳断裂，在大部分情况下首先会在连杆轴颈接近两边曲柄销的圆角处发生疲劳点蚀和轻微裂纹[22]，随后失效将会传递到两侧曲柄臂上，导致整根曲轴断裂。在特殊情况下，失效会发生在曲柄销和主轴颈接触的圆角处。因为在主轴颈的圆角处承受的压力主要是压应力，导致抗交变载荷能力增强。所以要准确的校核出曲轴的疲劳强度，就只需要对承受最大载荷的连杆轴颈圆角处进行疲劳强度计算就能达到要求。

根据应力准则来校核曲轴的疲劳强度，需要先找出危险疲劳点的最小应力σmin。因为曲轴的失效主要是由轴颈和平衡块的弯曲造成的，而并不是扭转形成的。图6可以看出，曲轴受到的最大应力将会是在连杆轴颈位于上止点时，气缸内点燃爆发的压力促使轴颈弯曲而形成。那么相对而言，连杆轴颈在下止点时所受的应力应该是最小的。所以，当曲轴第二连杆轴颈处于上止点时受到的应力应为最大，而第一连杆轴颈处于下止点时所受的应力应为最小，即为所要求的的最小应力。在二缸点火工况下，对于曲轴应力分析，进行有限元分析，得出的等效应力图如图16所示，轴危险点的最小应力σmin=6.13 MPa。

轴颈圆角的材料安全系数

(7)

(8)

(9)

(10)

(11)

(12)

(13)

式中：σ-1——零件材料的对称循环弯曲疲劳极限，根据结构钢曲轴预算[23]可用：σ-1=0.45σB。 可以得出σ-1=0.45×938=422 MPa；

σa——曲轴材料的弯曲应力幅，值见表5；

σm——曲轴材料的平均应力，值见表5；

Kσ——曲轴材料的轴颈圆角处应力集中系数。轴颈的过渡处的圆角处半径为R6，查阅文献[23]得出Kσ=1.4；

β——工艺强化系数，指不同的加工方法和工艺措施对曲轴圆角处的疲劳强度的影响[12]。在建模阶段中，此模型曲轴为摸段曲轴，查阅相关参数，得出β=1.1；

Ψσ——等效系数，其值与应力种类、表面状态及材料有关[23]。因为曲轴一般工况下都是旋转工作，则曲轴所受的是非对称循环载荷的极限应力。所以其工作应力也变成了非对称循环，即要计算不对称的平均应力对疲劳强度的影响；

σ0——脉动循环时材料的疲劳强度极限，查阅资料[23]得出σ0=1.5σ-1=1.5×422=633 MPa，将两个结果代入上述公式得出：Ψσ=(2×422-633)/633=0.33；

εσ——绝对尺寸影响系数。它表示实际的曲轴尺寸与试件不同时，两者疲劳极限相比的百分比。结构钢的值可经机械手册[23]查得εσ=0.6；

λ——动力强化系数，查机械手册[23]得出：二缸曲轴系数为1.07；

C——动载荷系数，一般系数取1.1～1.3，本文折中取1.2。

根据要求[23]，曲轴的疲劳安全系数要在1.3以上，文中求得S=3.9>[S]，即符合要求，则该曲轴的疲劳强度达到要求。σm、σa的数值见表5。

表5 σm、σa值

2.2 曲轴疲劳寿命计算

根据分析得出结果如图17所示，最大的周期为140 041，最大寿命发生在第二连杆轴颈的左侧曲柄，与主轴颈连接的圆角处，最小寿命在第二连杆轴颈右侧的曲柄右侧的圆角处。该疲劳分析曲轴的最小疲劳强度系数为2.298，说明强度系数为2.298时，曲轴在100 000 次循环交变应力的作用下，会产生疲劳失效当疲劳强度系数>1.0时，是符合强度要求的。

图17 曲轴的疲劳寿命Fig. 17 Fatigue life of crankshaft

根据上述的分析可知，曲轴上靠近自由端的曲柄、主轴和连杆轴颈安全；靠近输出端的部件寿命较短，安全度也较低，尤其是第二连杆轴颈处和主轴颈之间的和过渡圆角之间，是曲轴疲劳强度最为薄弱的地方。同时，连杆轴颈和主轴颈的过渡圆角处是应力集中的位置，该处应力最大，容易产生损伤，且经过多次的循环工作，损伤得到累加，所以容易破坏。

3 结论

本文利用NX中Nastran对曲轴进行网格划分和边界条件及载荷的施加，分析了曲轴的部件位移和应力状况，完成了曲轴的模态分析、疲劳强度计算和寿命的评估，通过分析得到：一缸点火下整体位移和等效应力均大于二缸点火，位移分别为0.089 5 mm和0.020 7 mm，等效应力分别为246.55 N和73.37 N；在X和Z向上位移变化均较小，Y向位移变化和整体位移变化趋势相同，且曲轴的强度均能满足性能要求。疲劳强度的分析得到：活塞在缸体的上止点时气体的爆发压力使得曲轴的弯曲应力最大，而在下止点时受到的压力最小。在连杆轴颈及主轴颈和平衡块相连接的过渡圆角处是曲轴所受应力最为集中的部位。在设计时，考虑改变平衡块的大小、刚度等来改善曲轴的振型变化。综合分析可知，应力集中多产生在圆角处，本文分析的结果为后续曲轴结构的改进，提供理论依据。