耦合地震动下地铁车站的动力响应研究

张 涵, 张西文

(1. 济南大学土木建筑学院, 山东 济南 250022; 2. 山东省城市地下工程支护及风险检测工程技术研究中心, 山东 济南 250022)

0 引言

近年来我国经济快速发展,地下空间大量兴建,特别是现阶段各大主要城市都在大规模地进行地铁建设,地铁也逐渐成为人们出行的主要选择。但我国处在地震的多发地带,例如1999年的台湾chi-chi[1],2008年的汶川地震[2],都对地下结构造成了严重的破坏。然而我国对地下结构的抗震研究起步较晚,地下结构抗震设计的相关规范也不够完善。

因此地下结构的抗震设计和与地震响应分析也成为众多学者的重要研究课题[3]。陈磊、谷音等[4-5]利用ABAQUS软件,对某车站进行了非线性地震反应分析。杜兴华等[6]分析了某车站在水平地震动作用下的内力和变形情况。刘庭金等[7]运用动力时程分析法对地铁车站进行了水平向的非线性地震响应数值模拟。Ni等[8]建立了地铁车站的二维模型,研究了车站在水平地震波下的塑形损伤和能量响应特征。上述研究都是将水平地震动视为地下结构破坏的主要原因,没有考虑竖向地震动以及耦合地震动的影响。

但近年来研究者已经开始逐渐关注竖向地震动对地下结构的地震响应。如张海[9]等开展了地震动输入方向对软土区车站结构响应影响的研究,结果表明竖向地震动对车站结构的内力和应力影响比较大。陶连金等[10]研究了大跨度高断面Y形柱地铁车站在竖向地震动下的地震响应规律,结果表明双向耦合地震动会增大结构的应力值,并对竖向位移产生影响。钟波波、Ma等[11-12]在对地铁车站进行地震响应分析时,均输入了水平、竖向和双向耦合三种形式地震动作为数值模拟的条件。

本文以某地铁车站结构为背景,使用有限元软件建立二维计算模型,利用EI-Centro波计算分析地铁车站在水平、竖向和双向耦合地震动作用下结构的抗震性能与地震响应规律。

1 地铁车站结构的有限元计算模型

1.1 模型建立

本文以2层3跨双柱地铁车站为背景进行地震响应分析。该车站高12.7 m、宽21.6 m。顶板厚度 0.7 m、中板厚度0.4 m、底板厚度1 m、外墙厚度0.8 m。两根纵向柱间距为5.4 m、直径0.6 m。此车站为箱型车站,车站的柱子在地震中为薄弱环节。因此为了计算简便选取地铁车站中带有中柱的关键断面,将三维模型转化为二维平面应变问题进行分析,具体结构剖面如图1所示。分别在水平方向上取四倍车站宽度的土体,竖直方向上取三倍车站高度的土体为研究对象,整体模型尺寸为200 m×55 m。在车站底部输入地震波,模型顶面为自由面,模型两侧设置为自由场边界,来模拟现实中两侧无限土体的效果。并采用0.5 m×0.5 m的矩形网格对地铁车站结构划分,2 m×2 m的矩形网格对土体划分,如图2所示。模型共计3 295个单元,3 519个节点。

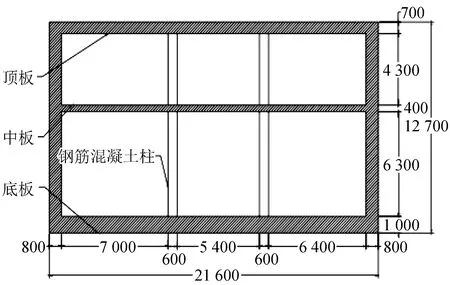
图1 结构剖面图(单位:mm)Fig.1 Structure section plan (Unit:mm)

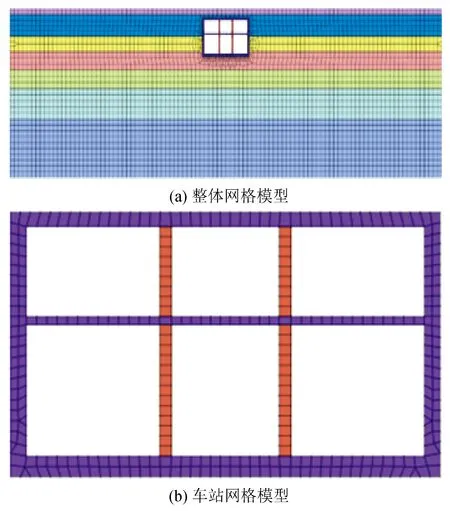
图2 车站及土体有限元模型Fig.2 Finite element model of station and soil

1.2 土层及结构参数

车站周围土体采用Mohr-Coulomb本构模型来模拟土的弹塑性,各土层参数见表1所列。地铁车站的混凝土结构采用弹性模型。车站主体结构中的外墙与中板采用C30混凝土,立柱采用C40混凝土浇筑。具体结构参数见表2。

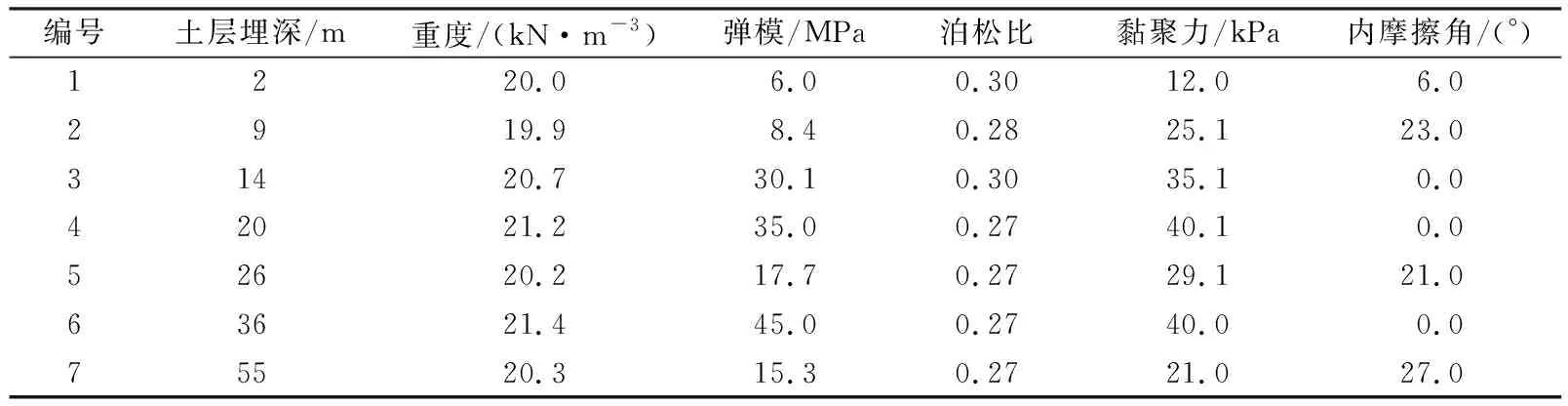
表1 土层参数

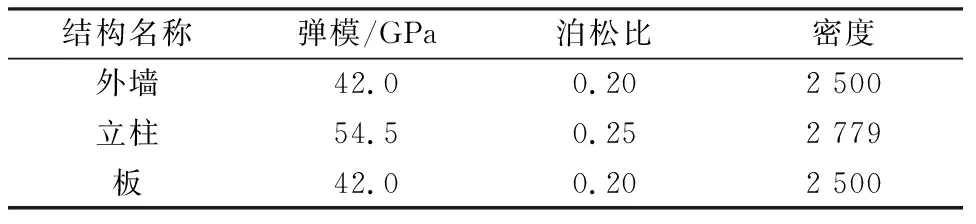
表2 车站结构力学性能参数

1.3 分析工况

选择具有代表性EI-Centro波作为地震动输入并截取25 s的地震动进行动力时程分析。水平、竖直地震动加速度时程曲线如图4所示。分析工况见表3。

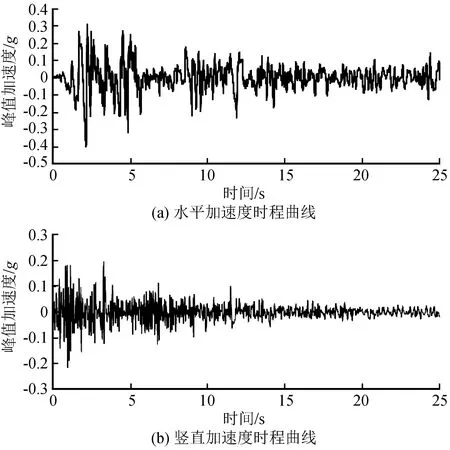
图3 EI-Centro波加速度时程曲线Fig.3 Acceleration time-history curve of EI-Centro wave

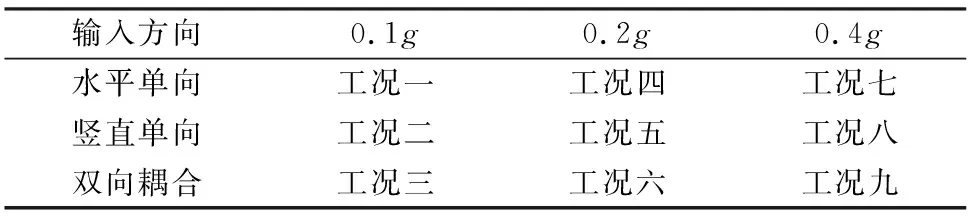
表3 分析工况

2 位移响应分析

分析车站结构在0.1g,0.2g,0.4g三种峰值加速度下的位移响应,同时定义侧墙上各点与底板的绝对水平位移之差为相对水平位移,中部底板点与底板最左侧点的绝对竖直位移之差为相对竖向位移。

2.1 水平变形分析

(1) 图4为车站顶板在0.2g峰值加速度下的相对水平位移时程图。从图中可以看出车站在水平单向与水平竖直耦合地震动输入两种情况下,曲线几乎完全重合而竖直地震引起的位移较小。说明结构顶板相对水平位移一般由水平方向地震动引起,竖直方向地震动对其影响较小。

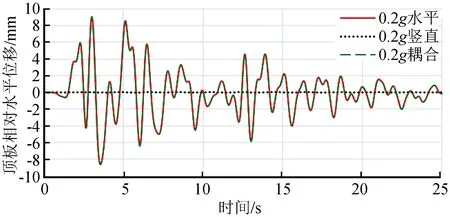
图4 顶板相对水平位移时程图(PGA=0.2g)Fig.4 Time history of relative horizontal displacement at station roof (PGA=0.2g)

(2) 图5为顶板在三种加速度峰值下的相对水平位移时程图。由图5可知随着地震加速度峰值的增加,顶板相对位移也会相应的增大,而在EI-Centro波这种地震波谱下,顶板会在2.98 s出现最大右摆位移(9.08 mm),3.52 s出现最大左摆位移(8.66 mm)。说明车站在2.98～3.52 s左右振动最大,动力响应最强烈。

图5 不同加速度峰值地震下顶板相对位移时程曲线Fig.5 Relative displacement time-history curves of station roof under different peak accelerations

2.2 竖向变形分析

(1) 图6为底板相对竖向位移时程曲线。从图中可以看出水平地震动输入下底板相对竖向位移略大于耦合地震动输入,且均大于竖向输入。可能由于在耦合地震动的输入条件下,竖向地震动会在一定程度上限制结构的竖向变形,从而影响结构的相对竖向位移。

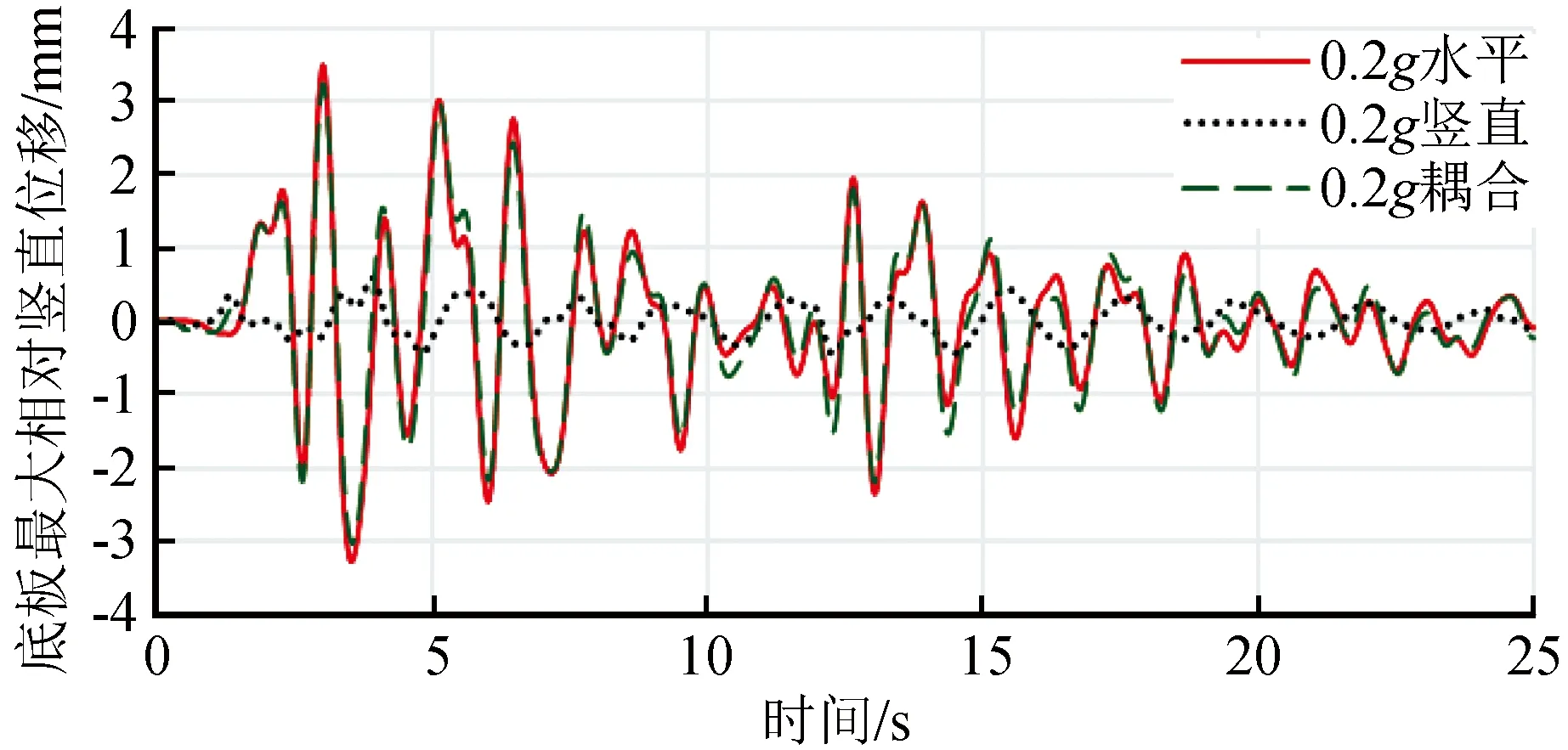
图6 底板相对竖向位移时程图(PGA=0.2g)Fig.6 Time history of relative vertical displacement at station baseplate (PGA=0.2g)

(2) 图7为底板相对竖向位移随底板宽度的变化图。从图中可以看出在竖向输入的情况下,车站底板的中部位置相对位移最大,并呈对称向两边递减,但其数值明显小于其他两种输入情况。而在双向输入与水平单向输入情况下,底板则是向单侧变形。底板相对竖向位移随底板宽度的变化也基本呈线性关系。说明在考虑底板相对竖向位移时,应选用耦合地震动作为输入条件,所获得的结果会更为准确。

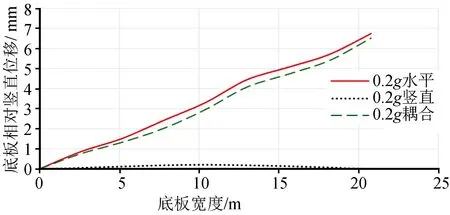
图7 底板宽度与底板相对竖向位移关系图Fig.7 Relationship between width of baseplate andrelative vertical displacement of baseplate

3 车站内力分析

3.1 应力云图分析

根据车站位移时程曲线,分析可得地震波峰值加速度为0.2g时车站结构在t=2.98 s出现最大水平位移,在t=3.94 s出现最大竖向位移。三种地震动输入的车站结构应力云图如图8所示。

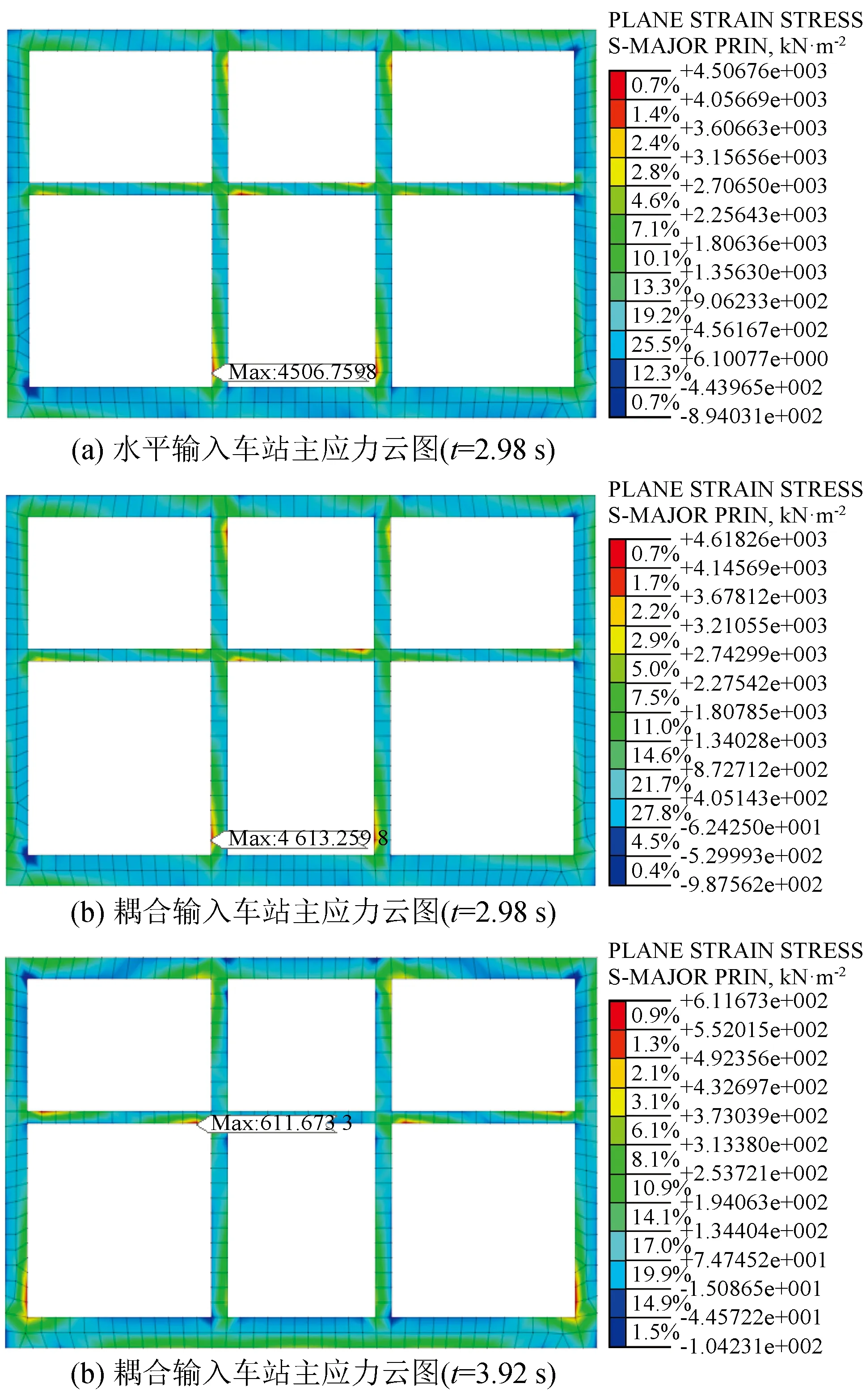
图8 车站主应力云图Fig.8 Principal stress of subway station

由图8可知,在三种地震波输入情况下,车站结构的主应力分布基本保持一致,均在负二层中柱底部出现了最大主应力,其数值在耦合地震波输入情况下最大,达4 613 kN/m2,较水平单向输入增大近2.4%。同时在中柱与中板、侧墙连接位置也出现了较大主应力,为结构的薄弱位置。

3.2 中柱主应力分析

为了便于结构中柱的主应力分析,在中柱布置了相应的监测点见图9所示。同时定义水平单向输入与双向耦合输入两种情况下所获得的中柱主应力的差值绝对值除以前者的数值为竖向地震动影响率。

表4为中柱各测点在水平单向与耦合地震动输入下的最大主应力,图10为中柱竖向地震动影响率。结果表明(1)中柱在水平单向输入下所产生的主应力略大于耦合输入下所产生的主应力,且在这两种地震动输入形式下,中柱应力值大小分布规律没有发生改变。即同一层的中柱下端主应力要大于上端,顶层中柱主应力要大于底层。(2)中柱竖向地震动影响率随着车站高度增加而减小。可能是由于竖向地震动向上传递,能量逐渐削弱从而影响减小。(3)中柱的竖向地震动影响率不受地震峰值加速度变化的影响。

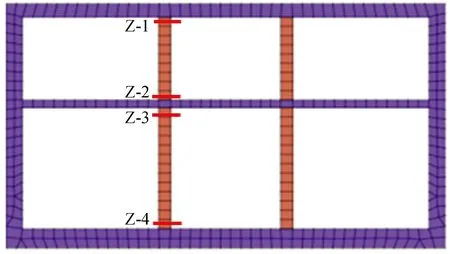
图9 中柱监测点Fig.9 Detecting points at middle column

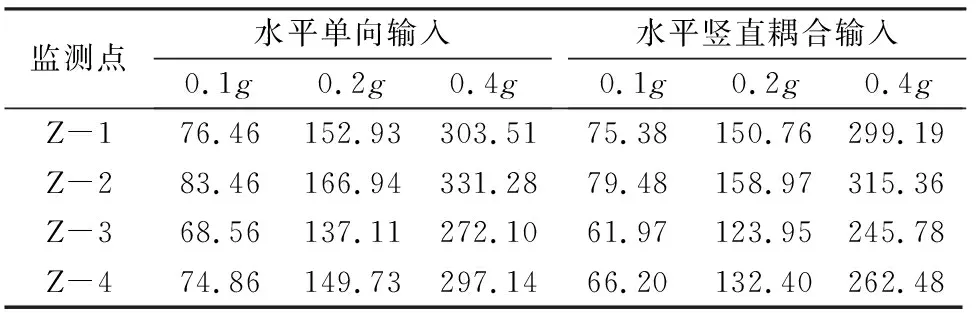
表4 中柱监测点主应力值(单位:kN/m2)

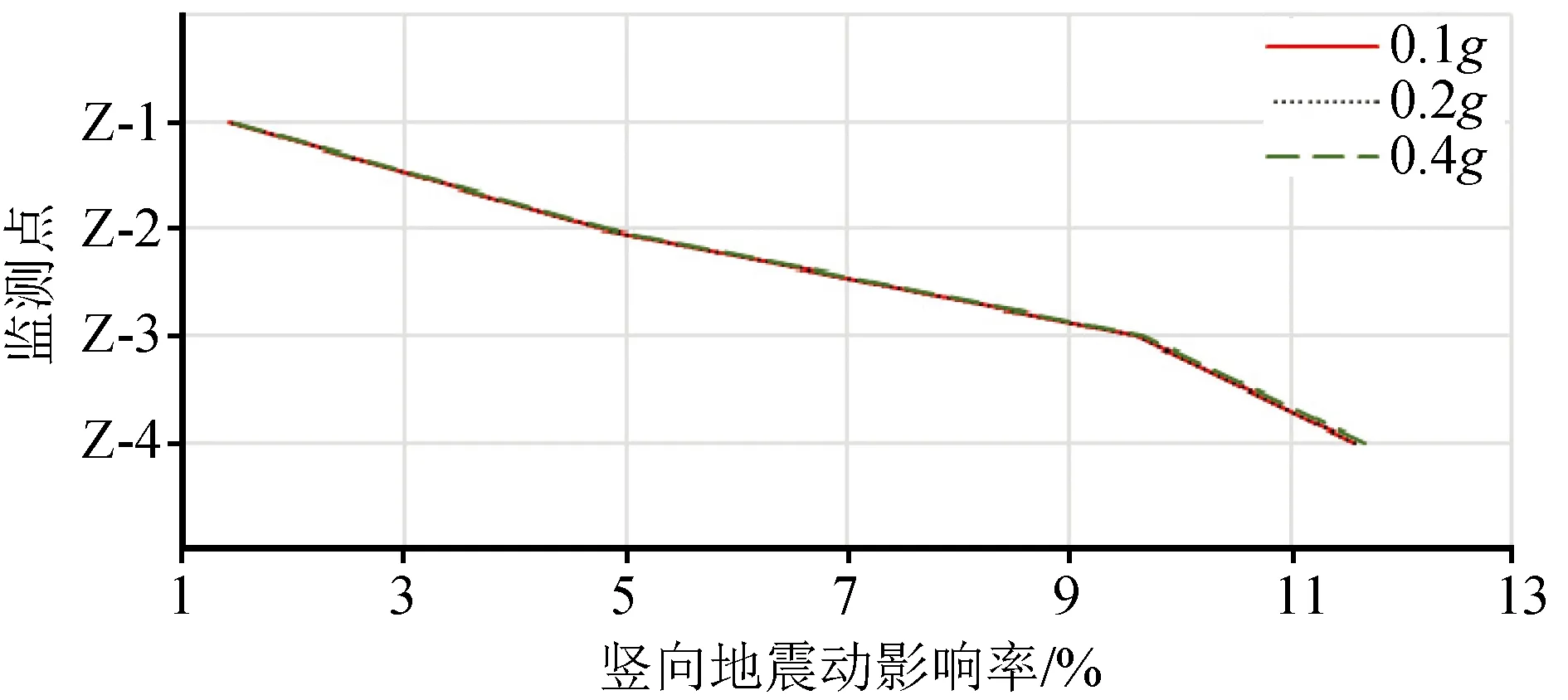
图10 中柱竖向地震动影响率Fig.10 Impact rate of vertical ground motion of middle column

4 结论

本文通过时程分析法,以某地铁车站为研究对象,分析其在水平、竖向和双向耦合地震动作用下的地震响应规律,得到以下结论:

(1) 耦合地震动对结构的相对水平位移影响较小,但会在一定程度上限制结构的竖向变形,对结构的相对竖向位移产生一定影响。

(2) 水平地震动作用下中柱主应力会略大于耦合地震动作用,且在这两种地震动输入形式下中柱应力值大小分布规律没有发生较大程度的改变;中柱的竖向地震动影响率不受地震峰值加速度变化的影响。

(3) 车站中柱底部,车站各节点位置在单向以及耦合地震动中都为结构的薄弱位置,需要在抗震设计中着重注意。