考虑边坡地形效应的地震动力响应分析

张迎宾, 柳 静, 唐云波, 相晨琳

(西南交通大学 土木工程学院, 四川 成都 610031)

0 引言

地震往往伴随着各种地质灾害,其中包括滑坡、泥石流、落石等,在复杂山区地震诱发的次生灾害更是严重威胁到人民的生命、财产等[1]。据统计调查,滑坡是地震发生前后产生数量最多的地质灾害[2]。地震诱发的滑坡对房屋、道路、桥梁等均会造成巨大的损失,因此地震条件下的边坡稳定性问题成为众多学者的重点研究方向[3]。

对地震作用下的边坡动力响应特征进行分析可为边坡稳定性研究提供依据。目前对地震边坡响应研究方法大致有实测地震分析、理论分析、试验研究和数值模拟等。Pedersen等[4]对法国阿尔卑斯山脉的Mont St.Eynard的地震数据进行了研究,发现在山脊侧面顶部相对于山脚谱比高达4.0;胡聿贤等[5]总结了我国在早期几次地震中观测到的由地形效应导致的宏观破坏现象;王宇等[6]、王思敬[7]、刘汉香等[8-9]通过振动台试验对坡体动力响应进行研究;景鹏旭等[10]通过ANSYS进行数值分析,发现边坡动力响应的非线性特征;刘春玲等[11]、李新平等[12]利用FLAC3D软件对边坡进行分析,均取得了丰富的成果。刘立波等[13]指出由于强震记录的限制,要利用实测地震分析出地形效应对边坡的响应影响有一定难度;振动台试验仍存在物理边界处理困难、费用较高、试验结果存在较大差异等问题。因此,数值模拟法是研究边坡动力响应的主要方法。

Ashford等[14]提出边坡的响应可细分为:地形放大效应、场地放大效应和表面放大效应。Zhang Yingbin等[15]通过研究了几何形状对三维边坡稳定性的影响,发现不同坡度、坡面会造成边坡稳定性差异。在地震作用下边坡地形效应研究方面,人们在实际的地震观测中很早也认识到地形会引起地表加速度的放大或者缩小,祁生文等[16]、秋仁东等[17]利用数值模拟法研究了边坡高度、角度对边坡动力响应的影响;张迎宾等[18]建立了曲面的类梯形山体模型,并进行了地震动力响应分析。已有研究对坡度、坡高等对边坡的地震响应方面的研究较多,但对于坡面形状的研究基本只存在于特定类型坡面的相关研究。为了对地形效应的影响进行较为全面而完整的研究总结分析,因此本文将通过FLAC3D数值模拟法,对二维边坡不同坡面几何形态下的地震响应规律进行研究。将地震能量以地震波的形式作用于坡体底部,根据加速度、速度放大比对地震响应情况进行讨论。

1 建立边坡模型

1.1 摩尔-库伦模型

本研究旨在对边坡动力响应问题进行探讨,需要材料在地震作用下能够发生塑性变形,已有相关研究表明边坡在静力作用下主要为“剪坏”,而动力作用下还包括“拉坏”[19-20]。因此,本文选取摩尔-库伦本构模型进行研究。

图1 摩尔-库伦本构示意图Fig.1 Mohr-Coulomb constitutive diagram

1.2 动力边界及阻尼设置

地震对边坡的作用表现为地震波在模型内的反射及折射,实际情况中,坡体反射的地震波可自由传播,而数值模型是采用一个有限范围模拟无限场地,因此在边界位置设置动力边界可吸收传来的地震波。

FLAC3D中采用静态边界(也称黏性边界)对边界上的入射波进行吸收,具体实现是通过在边界上施加法向和切向的阻尼器,从而对入射波进行吸收。当动力源在模型内部时,静态边界具有有效的作用,而本文动力源处于模型底部,静态边界不应用于沿网格方向的边界上,因为波的能量将从这些边界上“泄露”出去,故需要和“自由场边界”进行结合。本文的边坡模型的主体网格为非均匀状态,这时主体网格的运动和自由场网格的运动将不一致,这时边界上的自由场阻尼器将发挥作用,减少地震波在模型内的反射。

因此,为了研究边坡地形效应的地震动力响应规律,采用FLAC3D建立概化边坡模型,进行动力分析时采用静态边界和自由场边界相结合的形式,边界设置情况如图2所示。

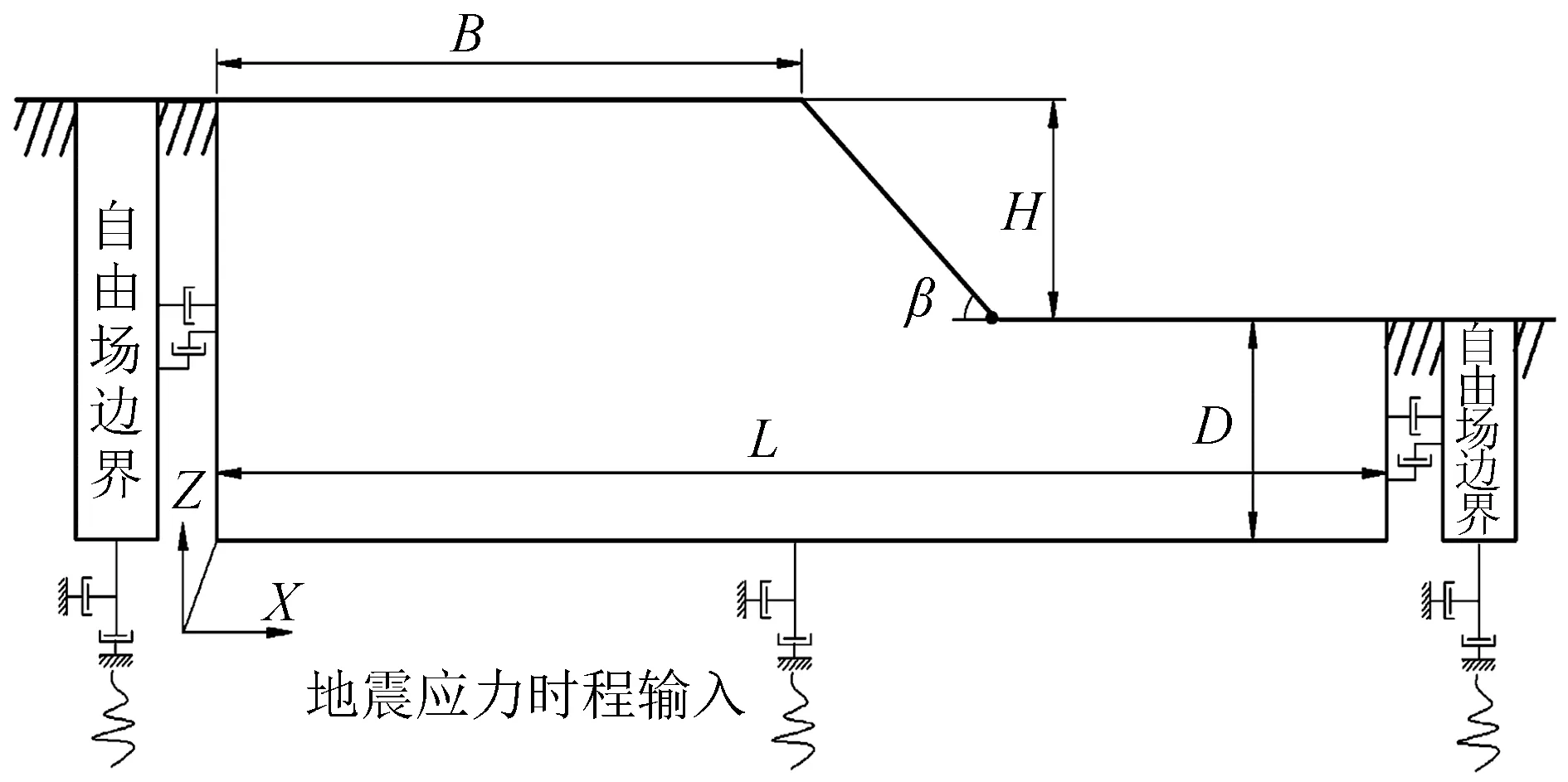
图2 边坡计算模型示意图Fig.2 Schematic graph of slope calculation model

FLAC3D中提供了三种形式的阻尼:局部阻尼、瑞利阻尼、滞后阻尼。局部阻尼通过长在简单模型中能得到较好的结果,本研究需要进行大量计算,且研究对象为均质化模型,相对较为简单,因此选用局部阻尼进行动力计算,阻尼系数取0.157。

1.3 地形效应模型

由于实际边坡中的材料构成较为复杂,为了便于边坡几何形态对响应的研究,因此将实际边坡形态进行了简化,且模型材料选用均质模型。材料参数以实际人工边坡强度为工程背景,参照《工程地质手册》(第四版)进行参数选取,各参数取值见表1。

表1 坡体材料参数

基于根据王健[20]、祝俊华[21]等对坡体形态的研究,将对坡高、坡角、坡面形状等三类因素分别进行固定变量分析。其中,考虑坡角因素时选用平面坡,坡高取40 m,坡度分别取:26.57°、45°、56.31°;考虑坡高因素时选用平面坡,坡角取45°,坡高分别取:20 m、40 m、60 m;考虑坡面形状因素时,坡顶与坡脚的连线与水平面呈45°夹角,坡高取40 m,坡面形态分别取:平面坡、凹型边坡、凸型边坡、阶梯型边坡。沿坡面从坡脚到坡顶布置6个测点,模型基本信息见表2所列,边坡模型示意图见图3～6所示。

表2 地形效应模型汇总Table 2 Summary of terrain effect model

图3 模型2示意图Fig.3 Schematic graph of model 2

2 地震动记录选取

现有的研究成果表明,坡体材料会对地震波中特定的频率进行放大,使得在这些频率内边坡的加速度放大明显,因此在地震波选取上,考虑具有不同中心频率的地震波。选用了如下三条地震波:Kumamoto波、Northridge波、El-Centro波。其中,Kumamoto波是2016日本熊本地震中由KMMH16台站监测到的E-W方向分量;Northridge波是1994美国Northridge地震中由Pacoima Dam (upper left)台站监测到的地震波中垂直于断层方向的水平分量;El-Centro波为1940年在埃尔森特罗地区记录到的第一条地震波。在地震波输入前对地震波进行滤波和基线矫正,滤波和基线矫正采用SeismoSignal软件进行低通滤波,最高频率取10 Hz。输入地震动幅值全部设定为地震峰值加速度PGA(Peak Ground Acceleration)=2 m/s2,输入地震波波形和傅里叶谱见图7。

图4 模型6示意图Fig.4 Schematic graph of model 6

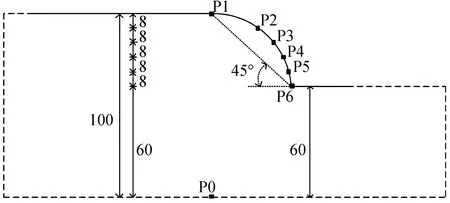
图5 模型7示意图Fig.5 Schematic graph of model 7

图6 模型8示意图Fig.6 Schematic graph of model 8

3 数值方法验证

为确保本文计算结果的合理性,首先对该数值模拟法进行验证。祁生文等[16]通过FLAC3D数值模拟方法对边坡动力响应规律进行了研究,得出的结果受到广泛认可。因此,首先建立了同祁生文等中相同的边坡模型,输入相同的地震动数据,如下:

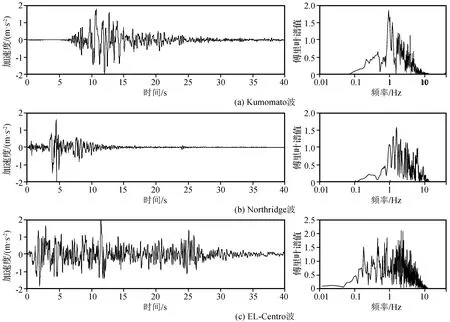
图7 输入地震波加速度时程和相应的傅里叶谱Fig.7 Acceleration time history of the input seismic wave and corresponding Fourier spectrum

(1)

(2)

式中:T为动力时间(s);g为重力加速度(m·s-2);T为周期(s);a为加速度时程 (m·s-2);v为速度时程(m·s-1)。

以数学绘本阅读课为例，1～3年级每周利用1学时阅读绘本故事。学校开展了相应的课例研究，邀请专家指导，从而探索出学科实践活动的有效模式。截至目前，学校已经积累了一系列典型课例，如一年级数学绘本《汪汪的生日派对》；二年级数学绘本《鸟儿鸟儿飞进来》《摇滚数学日》；三年级数学绘本《小鸡搬家》《游戏日》等。通过数学绘本故事这个媒介，大家深切感受到学生的数学学习兴趣被激发了出来。人文精神、学科融合运用使得学生的实践能力、创新能力在课堂中都自然地展现出来了，这就是学科实践活动课程的魅力。

地震输入将速度时程转换为应力时程输入模型底部,记录坡肩加速度时程,结果如图8所示。

由结果可知,加速度从模型底部传到坡肩为0.6 s,与祁生文等[16]一致,且加速度幅值也相同,在4.8 s的计算时间内共记录到20个周期振动与之一致,这说明本文采用的数值模拟计算方法正确可行,得出的结果具有合理性。

图8 坡肩加速度时程对比(左为祁生文等[16]结果,右为本文结果)Fig.8 Time-history comparison of accelerations at slope shoulder (The left is the result of Qi, et al[16], the right is the result of this paper)

4 边坡动力响应规律分析

地震边坡动力响应评价需要选取合理的指标,前人对于坡体响应的研究主要采用加速度、速度沿坡面放大比的形式,也有通过动荷载加载结束后的剪应变增量区以及残余位移云图进行分析,部分研究者还通过坡面记录到的加速度频谱特征进行成分变化比较,分析坡体的频谱特征[22-24]。通过以上方法,能够对地震波的作用进行有效评价,该种方法也广泛应用于边坡动力响应研究当中[25]。

本研究主要是针对不同边坡几何形态对边坡动力响应的影响进行分析,因此,以下研究通过加速度和速度放大比分析速度加速度沿坡面的分布情况,并通过沿坡面的加速度时程傅里叶谱分析坡体的频谱特征和坡体对地震波频谱特性的影响。

4.1 坡高对地震边坡动力响应的研究

利用以上选取的三条地震波分别作用在模型1,2,3(坡高分别为20 m,40 m,60 m)上,并监测其坡面的加速度及速度时程,并对地震波作用下的不同坡高坡面的PGA,PGV(Peak Ground Velocity)放大比进行分析,见图9～11。其中H(m)为坡高值,h(m)为每一监测点高度值,放大比指每一监测点的峰值速度、加速度值对坡脚的峰值速度、加速度之比。

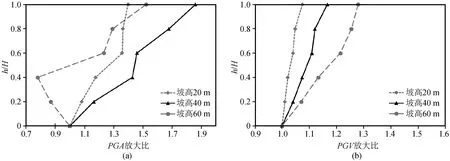
图9 Kumamoto波作用下不同坡高坡面PGA、PGV放大比Fig.9 PGA and PGV amplification ratios of slope surface with different slope heights under Kumamoto wave

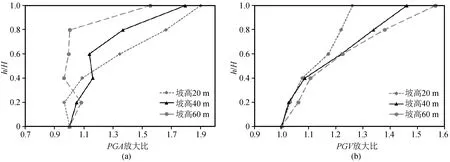
图10 Northridge波作用下不同坡高坡面PGA、PGV放大比Fig.10 PGA and PGV amplification ratios of slope surface with different slope heights under Northridge wave

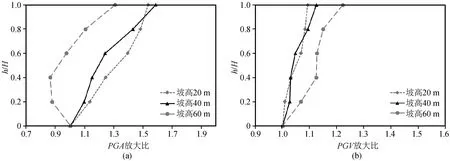
图11 El-Centro波作用下不同坡高坡面PGA、PGV放大比Fig.11 PGA and PGV amplification ratios of slope surface with different slope heights under El-Centro wave

由上述可知,不同坡高边坡模型沿着坡面向上的加速度值基本都在逐渐增加,这与Davis和West[26]基于1971年San Fernando 地震的余震监测数据中的现象一致。同样由结果可得出坡面记录到的PGV值也随着高度增大而增大。对比不同地震波作用下坡面的加速度和速度放大比,可以看出在Northridge波作用下速度放大比更加明显,这与地震波的强度及频谱特性有关。观察不同坡高的加速度放大比,发现60 m坡高整体放大性小于20 m及40 m。这说明,在采用坡顶与坡脚的加速度放大比对比时,坡高的增加并不会导致放大情况更明显。而对于速度放大情况而言,可发现大致呈现出坡高越高边坡放大情况越强的趋势。

分析不同高度边坡坡顶和坡脚水平向加速度傅里叶谱值图可看出,在坡高为20 m时,坡顶相比坡脚的傅里叶谱值放大较少;在坡高为40 m,60 m时,坡顶相比坡脚谱值放大较多。不同地震波在同一模型中,傅里叶谱放大范围不尽相同,但都包括了模型的自振频率。可见不同自振频率的模型,会对地震波中相应频段进行放大,不同地震波傅里叶谱放大范围不同。

4.2 坡角对地震边坡动力响应的研究

坡角的大小决定了地震波在坡面的反射和折射角度,可直接影响地震能量在坡体内部的传播情况。同样将Kumamoto、Northridge和El-Centro三条地震波分别作用在模型2,4,5(坡高均为40 m,坡角分别为45°,26.57°,56.31°)上,并监测其坡面的加速度及速度时程,速度、加速度放大比结果如图13～15。

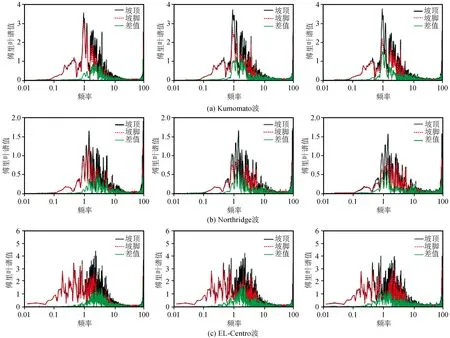
图12 不同坡高坡顶/脚傅里叶谱Fig.12 Fourier spectrum at slope top/foot with different slope heights

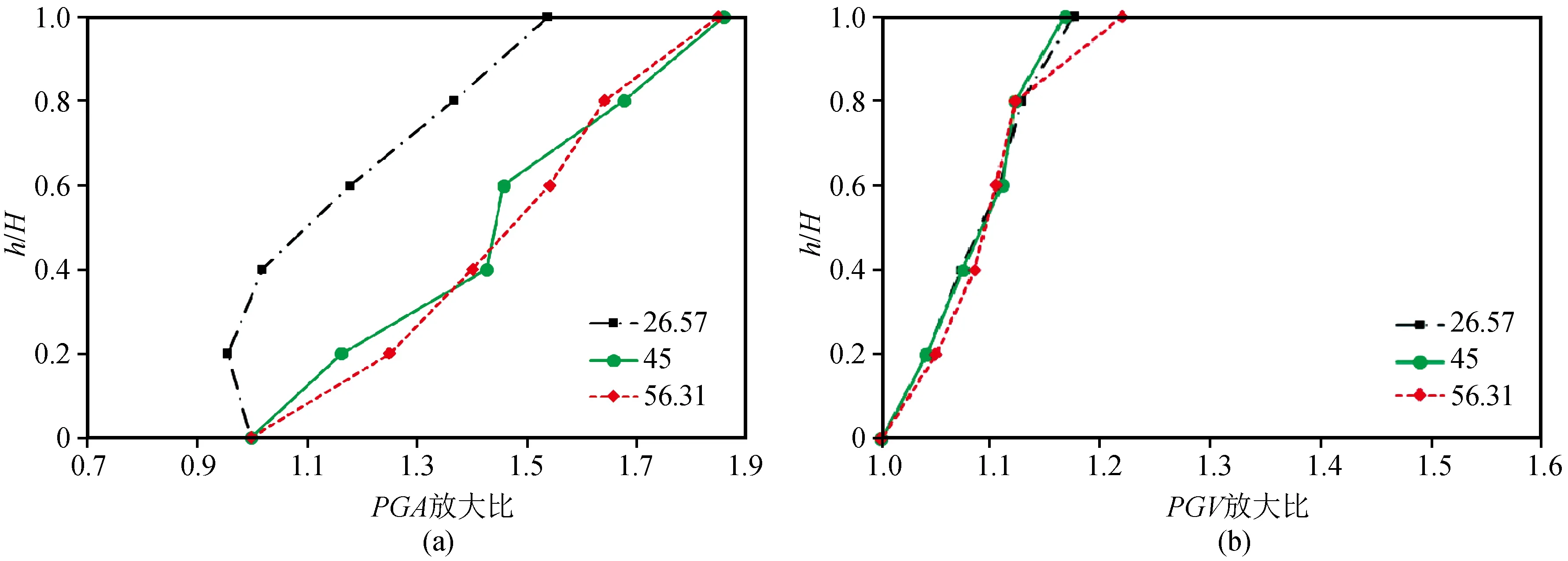
图13 Kumamoto波作用下不同坡角坡面PGA、PGV放大比Fig.13 PGA and PGV amplification ratios of slope surface with different slope angles under Kumamoto wave

图16比较了不同坡角的边坡坡顶和坡脚的傅里叶谱分布情况,由图可看出不同边坡模型傅里叶谱值放大范围不一;比较不同坡角放大情况,由坡顶与坡脚傅里叶谱差值可以看出坡角越大傅里叶谱差值越大。

4.3 坡面形状对地震边坡动力响应的研究

根据前人对实际地震观测结果,可知坡体表面的突出位置可能更容易受到地震的破坏,不同的坡面形状使得地震能量在坡体内部产生差异化分布,使得坡面不同位置地震响应的情况不同。因此,仍利用以上三条地震波分别作用在模型2,6,7,8(坡高均为40 m,坡角均为45°,坡面形状分别为平、凹、凸、阶梯形),根据其加速度、速度放大比结果(见图17～19),发现在不同坡面形状下坡顶加速度和速度相对于坡脚都有不同程度放大。

图14 Northridge波作用下不同坡角坡面PGA、PGV放大比Fig.14 PGA and PGV amplification ratios of slope surface with different slope angles under Kumamoto wave

图15 El-Centro波作用下不同坡角坡面PGA、PGV放大比Fig.15 PGA and PGV amplification ratios of slope surface with different slope angles under Kumamoto wave

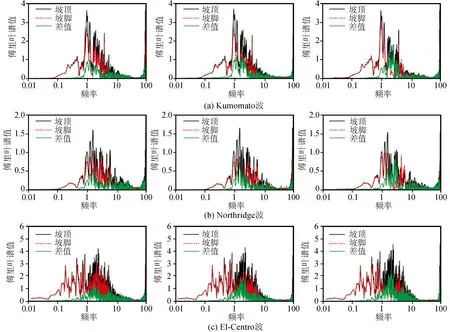
图16 不同坡角坡顶/脚傅里叶谱Fig.16 Fourier spectrum at slope top/foot with different slope angles

整体对比可知,凹坡加速度放大比小于其他坡形。而凹坡在坡顶处的速度放大比大于其他坡形,但放大比分布规律与其他三种坡面形状大概一致。

从凹型坡来看,可知在不同地震输入下凹型坡在顶部的加速度放大比和速度放大比增量较大,而在坡体中下部位置增量较小一些,甚至出现加速度减小的情况,这说明凹型坡坡顶更容易发生破坏。由凸型坡结果可发现,凸型坡在顶部得加速度和速度放大比增量较小,而在坡体中下部其增量较大,在坡脚位置增量最大,由此可见凸型坡在坡体中下部地震响应更强烈。对于平面型坡和阶梯型坡来看,其加速度和速度放大比沿坡面分布较均匀,都随着坡高的增大而增大。而Northridge波作用下的阶梯型坡在坡脚附近出现了极大的加速度值,这说明在地震作用下突出的阶梯构造可能为造成更大的加速度响应。

图17 Kumamoto波作用下不同形状坡面PGA、PGV放大比Fig.17 PGA and PGV amplification ratios of slope surface with different slope shape under Kumamoto wave

图18 Northridge波作用下不同形状坡面PGA、PGV放大比Fig.18 PGA and PGV amplification ratios of slope surface with different slope shape under Northrige wave

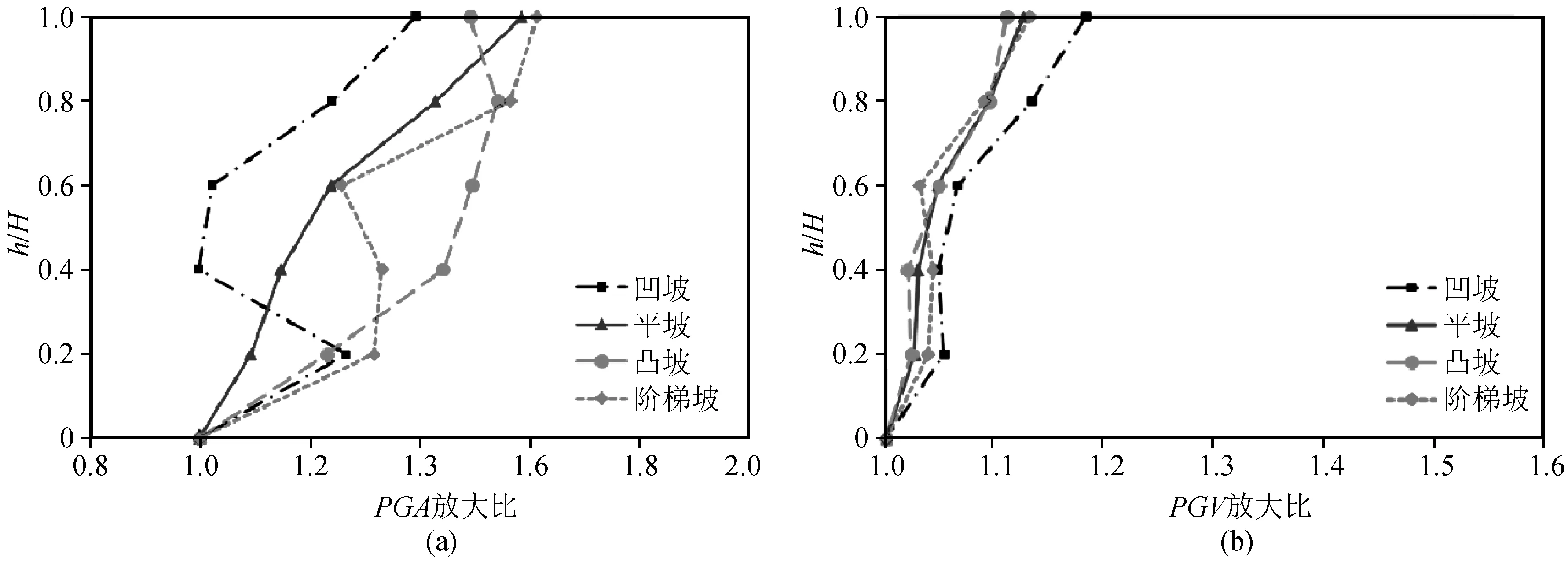
图19 El-Centro波作用下不同形状坡面PGA、PGV放大比Fig.19 PGA and PGV amplification ratios of slope surface with different slope shape under El-Centro wave

图20 不同坡面形状坡顶/脚傅里叶谱Fig.20 Fourier spectrum at slope top/foot with different slope shapes

观察图20不同坡面形状下边坡的坡顶、坡脚的傅里叶幅值谱发现,坡顶相对于坡底的频谱放大主要集中在1～3 Hz之间,模型自振频率1.67 Hz也包含在这个范围内。在对相同的模型输入不同的地震波时,傅里叶谱值的放大范围也不完全一致,说明傅里叶谱的放大不仅与模型有关,还和输入的地震波频谱性质有关。整体上比较凹面坡的傅里叶谱差值较其他两种坡面形状小,这与加速度放大比分布情况一致。比较凸面坡和阶梯状坡在坡顶和坡脚傅里叶差值上基本一致。

5 结论

综上,本文进行了从坡脚到坡顶的不同位置的加速度、速度放大比分析,完成了边坡的坡高、坡角、坡面形状等效应下的地震动力响应分析,得出以下几点结论:

(1) 不同坡高的模型的加速度和速度放大比大致都沿坡面向上增加,其中加速度放大比的增量与坡高的高度无明显相关性,而边坡速度放大效应随着坡高的增加而更加明显。

(2) 坡角对加速度放大明显。

(3) 不同的坡面形状会影响坡面加速度、速度的分布规律,其中凹面坡的加速度放大较小,但在顶部速度放大增加剧烈;而凸面坡在坡体的中下部加速度放大更加明显;阶梯坡、‘平’坡在加速度和速度响应相当,但阶梯型坡突出的阶梯构造使得加速度放大更大。

(4) 在选取的三条地震波中,发现Northridge在该研究中产生的加速度和速度放大效应比其他两条波更加明显,这说明地震波的某些特性对边坡响应的影响也较大。

由此可见边坡的地形效应是影响边坡响应的重要因素,且不同的坡面形状会造成不同的加速度响应规律,因此在进行边坡地震稳定性评价和边坡设计中应加以考虑。但本文采用的计算模型为均质模型,与实际边坡的复杂构造差异较大,因此地形效应对地震边坡动力响应的研究还需要对具体的边坡工程进行分析,而且若能进行三维下的边坡地形特性的对边坡动力响应的研究则可得出更加具体的结果。