三维椭球形盆地对球面波的散射

冯 亭, 刘中宪,2, 黄 磊, 刘明珍

(1. 天津城建大学土木工程学院, 天津 300384; 2. 天津市软土特性与工程环境重点实验室, 天津 300384;3. 天津大学建筑工程学院, 天津 300372; 4. 青岛上流远大住宅工业有限公司, 山东 青岛 266041)

0 引言

震害研究表明,局部场地对强地震动有明显的放大效应[1-3],其本质是地震波在传播过程中发生复杂的散射、衍射、相干作用以及波型之间转换等。国内外众多大中城市坐落在沉积盆地之上,或者许多城市内分布着古河道,由于沉积盆地卓越周期长,对于自振周期长的大跨桥梁、高层建筑等结构物在地震中造成更为严重的破坏,所以灾害性地震中往往这些城市的经济损失、人员伤亡严重。

该问题的定量分析方法有解析法[4-6]和数值法(有限单元法[7]、边界单元法[8-9]和离散波数法[10])。关于沉积盆地对弹性波的散射问题,Trifunac[11]采用波函数展开法模拟分析了半空间中二维沉积盆地SH波的散射影响;刘殿魁等[12-13]利用复变函数法对平面SH波入射凹陷盆地的散射问题进行了解析求解;Lee[14]利用球波函数展开法对弹性波入射半球形沉积盆地的散射问题进行了模拟分析,但该模拟仅限于低频波散射的解答;Bouchon[15],Kamalian[16],Zhao and Valliappan[17],模拟分析了二维沉积盆地对弹性波散射的影响,根据所得结果对影响局部场地(沉积盆地)放大效应的参数进行了详细分析;Mossessian and Dravinsk[18]、Sanchez-Sesma and Luzon[19]利用间接边界积分方程方法对弹性波入射三维沉积盆地半空间的散射情况进行了模拟分析,结果显示三维散射情况与二维散射情况差异显著,进行三维盆地场地效应分析,更接近实际情况。

值得指出的是,以上文献对沉积盆地的地震响应研究主要针对平面波散射情况,沉积盆地对球面波散射问题目前研究较少,当波源距离较近时,入射波曲率对地震动的影响不可忽视,因此对球面波散射问题的研究显得尤为重要。另外,目前对于三维沉积盆地对弹性波散射问题的研究多针对低频波,然而高频波对结构物的抗震性能影响不能忽略,且三维沉积盆地对高频弹性波散射的研究还不够系统深入,因此利用高精度数值模拟方法对三维沉积盆地对球面波散射问题在宽频段情况下进行系统的参数分析和规律探讨是有必要的。

本文针对三维沉积盆地对球面波散射的宽频问题,建立了一种新的快速宽频边界元法。在GMRES迭代求解过程中,只有计算残值向量和矩阵向量乘运算时才需要存储系数大矩阵,通过修改GMRES迭代计算格式求解线性方程组,把存储量降低到与计算自由度成正比[O(N)]。另外,应用OpenMP+MPI混合并行编译模型,实现多核SMP集群的并行运算,提高了计算效率。基于该方法着重探讨了入射波频率、波源与盆地距离等参数对沉积盆地地震动放大效应的影响规律,研究结论对于沉积盆地区域城市的规划建设、大中型工程抗震设计等具有一定的参考价值。

1 计算模型

均质半空间中存在一半椭球形沉积盆地,如图1(a)所示,以盆地中心地表点为坐标原点o建立直角坐标系,三维椭球形沉积盆地的几何表达式如下:

x=axcos(β)cos(φ)

(1)

y=aycos(β)sin(φ)

(2)

z=hcos(β)

(3)

式中:β表示交界面S0上任一点与z轴的夹角;φ表示交界面S0上任一点在xoy面的投影点与x轴正方向的夹角,0≤β≤π/2,0≤φ≤2π ;ax表示沉积盆地沿x方向的半宽;ay表示沿y方向的半宽;h表示沉积最大深度。

图1 三维沉积盆地计算模型Fig.1 Three-dimensional sedimentary basin calculation model

基岩半空间域设为E,三维沉积盆地域设为R,半空间域E与沉积盆地域R交界面设为S0,半空间地表面设为S2,沉积盆地地表面设为S1,区域R和E的介质均简化为均匀、各向同性和线弹性。假设入射一球面波,在沉积盆地交界面将发生散射(衍射),波源埋深dz取10 km,波源与盆地正下方O1点的垂直距离设为ds。

本文利用全空间格林函数进行间接边界元方法计算,采用ANSYS软件建立模型,利用四边形单元离散网格,如图1(b)所示。为了满足计算精度要求,考虑散射波的衰减效应,离散范围一般情况下取5倍的波长就能满足,本文计算范围取为4ax。为保证弹性波散射的求解精度,一个波长至少离散10个单元,本文经过计算对比不同离散精度的模型,结果已经计算稳定。值得指出的是本文方法适用于模拟任意形状的沉积盆地,而本文暂以一半椭球形沉积盆地为例进行模拟分析。

2 频域响应计算

针对三维地形对地震波的散射,本文利用全空间格林函数进行间接边界元法模拟求解,计算区域介质假设为均匀各向同性、线弹性。不受体力作用情况下,弹性波在弹性各向同性固体介质中的位移场稳态波动方程为:

日前，天津滨海新区通报了12起不作为不担当的典型案例，集中表现出的问题主要有：党的建设弱化，坚持以党的政治建设为统领力度不够，履行全面从严治党责任不力，管党治党“宽松软”；形式主义、官僚主义问题突出，贯彻上级决策部署打折扣，执行政策“中梗阻”；群众意识淡漠，服务发展服务群众不积极，不思进取“躲推绕”；落实扶贫助困政策不到位，装聋作哑当“木官”；推进生态环境治理不主动，履行安全生产管理服务职能不到位；执行纪律制度规定不严格，作风漂浮“庸懒散”，等等。

(λ+μ)·u+μ2u=-ω2u

(4)

式中:λ、μ为介质的拉梅常数;为矢量微分算子;u=(u,v,w)为位移矢量;ω为简谐波运动频率,时间因子exp(iωt)已略去。

基于单层位势理论,三维空间域内一点的散射波场位移和牵引力可表达为某边界连续面S上的积分:

(5)

(6)

式中:Gij(x,y)是位移格林函数,表示由作用在y处j方向的一单位力引起的x处i方向的位移;Tij(x,y)是应力格林函数,表示由作用在y处j方向的一单位力引起的x处i方向的应力;φj(y)可看作在边界面S上y处j方向上作用的虚拟荷载密度。

2.1 波场分析

根据间接边界元法(IBEM)基本原理可知,基岩半空间域总波场是由自由场和散射场叠加构成,沉积盆地域总波场只由散射场构成。自由波场是指球面P波入射不包含沉积盆地域时的基岩半空间域的波场解答。根据惠更斯原理,散射波场是指在沉积盆地交界面和所取计算区域的基岩半空间自由地表面施加虚拟均布荷载构成。

则,基岩半空间域位移:

(7)

(8)

(9)

(10)

2.2 边界条件及求解

(1) 沉积盆地域地表面S1与基岩半空间域地表面S2的应力自由边界条件为:

(11)

(12)

把式(6)代入式(11)、(12)可得:

(13)

(14)

式(14):基岩半空间地表面S2上的自由波场应力为空。

(2) 沉积盆地交界面上的位移应力连续边界条件为:

(15)

(16)

把(9)、(10)式分别代入(15)、(16)式可得:

(17)

(18)

求解时需要离散沉积盆地交界面和整个自由地表面,并且在每个离散单元上施加虚拟均布荷载。覆盖在离散单元上的斜面圆盘中心位置设为xm,虚拟均布荷载中心表示为ym,基岩半空间域的表面离散单元数设为N1,沉积盆地域地表面离散单元数设为N2,沉积盆地交界面离散单元数设为N0,假设虚拟荷载密度φj(ξ)为常量,则公式(13)、(14)、(17)、(18)的离散化线性方程如下所示:

(19)

(20)

(21)

(22)

以上离散化方程最终可整理成为(6N0+3N1+3N2,6N0+3N1+3N2)阶的线性方程组,求解该线性方程组得到虚拟波源密度,进而可得到各离散点处的位移,再通过(7)、(8)式计算可得总的位移场。

文中已经过多次不同离散程序的设计对比,结果均已收敛,且以半球形均质沉积盆地模型为例,对程序编制的精确性进行了检验,精度检验详见第3部分。另外考虑到(5)、(6)式积分时有奇异点存在,本方法中采用了一个与离散单元面积等效的斜面圆盘,并在其上施加均布荷载,并利用格林函数展开式求解,来解决积分奇异性问题。

3 精度检验

为检验程序编制的精确性,本文以半球形均质沉积盆地模型为例。将球面波设于沉积盆地正下方无限远处(取dz=100 km),退化为平面P波垂直入射情况,将模拟结果与Mossenssian和Dravinski[18]给出的结果对比。计算参数取值:沉积盆地和基岩半空间的泊松比v2=v=1/3,沉积盆地与基岩半空间介质剪切波速比v2/v=0.5,密度比ρ2/ρ=2/3,材料黏滞阻尼比ξ=0.01,定义无量纲频率为散射体等效直径与入射波波长的比值,即:η=2a/λ=ωa/πcs=0.75,a为沉积半径,λ为半空间入射波波长,cs为基岩半空间剪切波速。从图2可以看出本文方法的计算结果与文献给出的结果两者吻合良好,由此验证了本文方法的计算精度。

图2 本文计算结果与Mossessian and Dravinsk所得地表位移幅值对比Fig.2 Comparison between the surface displacement amplitudeobtained by Mossessian and Dravinsk and thecalculation results in this paper

4 算例与分析

基于快速宽频间接边界元法,针对基岩半空间内三维半椭球形沉积盆地对球面波的散射进行研究。波源埋深取dz=10 km,考虑波源与盆地垂直距离的变化ds=0、2 km、5 km、10 km、50 km,入射波频率取η=0.5、2.0、5.0。沉积盆地和基岩半空间的泊松比为v2=v=1/3,沉积盆地与半空间介质剪切波速比V2/V=0.5,密度比ρ2/ρ=2/3,材料黏滞阻尼比分别为ξ=0.02、ξ=0.01。为保证弹性波散射的求解精度,一个波长至少离散10个单元,具体离散单元数为:①当η=0.5、2.0时单元数为9 351。②当η=5.0时单元数为36 765。符号表示与精度验证部分相同。

4.1 三维沉积盆地地表位移幅值单频分析

图3到图5分别给出了膨胀波源在波源埋深与无量纲频率相同的情况下,不同水平位置处地震波的放大效应和空间分布状态,并将结果与相应的平面波结果[9]进行对比分析。其中无量纲频率η=0.5、2.0、5.0。在图中位移幅值是用相应自由场(无沉积盆地存在)最大竖向位移幅值标准化。

首先考虑在同一水平位置(膨胀波源位于沉积盆地正下方ds=0)处,不同入射波频率下,对地震波的放大效应和空间分布状态的影响。从图中可以看出,①较低频率(η=0.5)膨胀波入射下,主方向(z向)位移呈现聚焦效应,位移最大值集中在盆地中心位置,且位移幅值从盆地中心到边缘位置逐渐减小。②高频波(η=2.0,5.0)入射时,主方向位移出现波峰波谷交错现象,这主要是由于从盆地底部透射的体波与盆地内体波转换的面波产生的干涉效应。③频率η=0.5时,盆地内部主方向位移相对于基岩半空间的放大效应不明显,位移幅值仅为2.15,与自由场位移接近。入射波频率越大,沉积盆地相对半空间的放大效应越显著,且干涉效应越强烈,例如,η=5.0时,盆地中心位置处z向位移峰值达到21.7。④沉积盆地次方向(x、y向)位移出现两点聚焦效应,随着频率增大,聚焦区域减小。将以上结果与相应平面波结果[9]对比发现地表位移幅值一般小于平面波入射情况,例如η=2.0,平面波入射时地表位移幅值为9.8,而球面波入射时地表位移幅值为7.6。

考虑膨胀波源水平位置变化,①高频波(η=2.0,5.0)入射时,当波源到盆地水平距离较小(ds小于5 km)时,盆地主方向位移仍出现波峰波谷交错现象,η=5.0,ds=2 km时,z向位移幅值达到18.2。②靠近点源一侧区域主方向位移放大效应高于远离点源一侧区域,如η=2.0,ds=5 km时盆地左侧区域主方向位移放大效应明显高于右侧。③受膨胀波源曲率对波的散射影响,当波源水平距离较近时,主方向位移波峰波谷是围绕盆地中心呈圆环状交替出现,但当入射波频率较高,波源水平距离较远时,如:η=5.0,ds=50 km时,主方向位移波峰波谷呈纵向交替呈现。这种相邻区域地震动放大效应的差异性已被多次地震观测记录所证实,对于较大规模沉积盆地地震区划需要考虑其内部地震动的差异性。④整体来看,随着波源与盆地水平距离增大,地表主方向最大位移幅值降低,例如:入射波频率η=5.0,波源水平距离ds=0时,盆地中心位置处z向位移幅值达到21.7,波源水平距离ds=50 km时,z向位移仅为1.3。⑤点源位置对次方向位移幅值分布影响较大,随着点源水平距离增大,次方向位移聚焦区域增加,且聚焦区域分布更分散。⑥高频波入射时,次方向位移出现一定的边缘效应,如η=5.0,ds=50 km时y向位移幅值为1.24,这是由于盆地底部透射的体波和盆地内部由体波转换为的面波以及从盆地边缘处透射的体波相互叠加而出现的现象。⑦高频膨胀波入射时,点源水平距离在10 km以内时,主方向、次方向最大位移幅值均相差不大,但点源水平距离ds=50 km时,主、次方向最大位移幅值均降低很多,如入射波频率η=5.0,波源水平距离ds=5 km时,z方向最大位移幅值为12.1,x方向最大位移幅值为5.46;波源水平距离ds=50 km时,z方向最大位移幅值为1.21,x方向最大位移幅值为0.87。

图3 膨胀波源不同水平位置处半椭球形沉积盆地地表位移云图(η=0.5)Fig.3 Surface displacement nephogram of semi-ellipsoid sedimentary basin at different horizontal location of the compressional wave source (η=0.5)

图4 膨胀波源不同水平位置处半椭球形沉积盆地地表位移云图(η=0.2)Fig.4 Surface displacement nephogram of semi-ellipsoid sedimentary basin at different horizontallocation of the compressional wave source (η=0.2)

图5 膨胀波源不同水平位置处半椭球形沉积盆地地表位移云图(η=5.0)Fig.5 Surface displacement nephogram of semi-ellipsoid sedimentary basin at different horizontallocation of the compressional wave source (η=5.0)

4.2 膨胀波源不同水平位置处沉积盆地地表位移幅值谱分析

三维沉积盆地对膨胀波的散射作用非常复杂,为了更全面反映波源水平位置对膨胀波散射的频谱特性,图6、7分别给出了膨胀波源入射下沉积盆地地表沿坐标轴上几个典型点位的位移幅值谱。其中η∈(0,5.0),本文假设膨胀波源位置沿x轴负方向变化,则观察点位取x轴上x/ax=-0.8,-0.5,0.0,0.5,0.8,y轴上y/ay=0.0,0.5,0.8。

从图中容易看出,①当膨胀波源位置为ds=50 km时,沉积盆地地表不同点位位移幅值较小。②当膨胀波源与沉积盆地水平距离较近(ds≤10 km)时,在较低频率(η=0.8)时,沉积盆地地表不同点位的主方向位移幅值差别不大且位移放大效应较小;在较高频率域内,沉积盆地地表不同点位的位移频谱特性差别很大,这主要是由于沉积盆地对膨胀波的散射作用,以及散射波之间复杂的相干效应。与平面波入射情况相比,球面波入射之下地表位移幅值谱曲线均有所降低。

图6 膨胀波源不同水平位置处半椭球形沉积盆地地表x轴上位移幅值谱[Plane(y=0)]Fig.6 Displacement amplitude spectrum on x axis of the surface of semi-ellipsoid sedimentary basinat different horizontal position of the compressional wave source [Plane(y=0)]

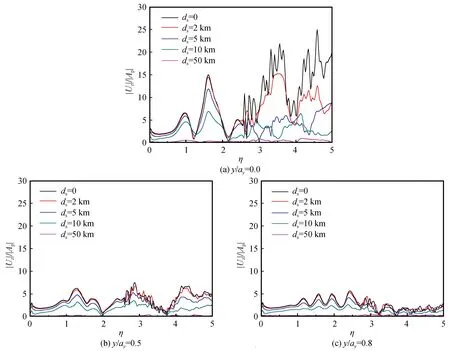
图7 膨胀波源不同水平位置处半椭球形沉积盆地地表y轴上位移幅值谱[Plane(x=0)]Fig.7 Displacement amplitude spectrum on y axis of the surface of semi-ellipsoid sedimentary basin at different horizontal position of the compressional wave source [Plane(x=0)]

考虑膨胀波源水平位置变化:①整体来看,沉积盆地地表主方向位移,随着入射波频率增大,位移频谱曲线震荡越剧烈,且随着膨胀波源与沉积盆地水平距离越近,位移幅值频谱值也基本越大。②不同点位处,第一阶峰值频率均在η=1.0附近,不同膨胀波源水平位置下,第一阶峰值频率基本一致,说明对于同一种入射波,不同波源位置下,位移“共振”频率基本相同。③沉积盆地地表中心区域点位的位移幅值谱值一般大于其他点位。表明沉积盆地地表位移聚焦效应一般位于盆地中心区域。对该模型(沉积盆地与半空间介质剪切波速比V2/V=0.5),沉积盆地地表主方向位移谱峰值达到24.9。④膨胀波源与沉积盆地水平距离较近(ds≤5 km)时,沉积盆地中心区域点位位移幅值在高频段内达到峰值,因此当膨胀波源与盆地水平距离较近时,在实际工程中应特别注意沉积盆地对高频段波的放大效应。

5 结论

三维半椭球形沉积盆地对球面波散射的地震动特性依赖于入射波频率、膨胀波源水平位置等因素。数值结果研究表明:

(1) 整体来看,随着膨胀波源与盆地水平距离增大,地表主方向最大位移幅值降低,地表次方向位移聚焦区域增加且分布更分散。

(2) 膨胀波源水平位置为ds=0时,较低频率膨胀波入射下,地表主方向位移呈现聚焦效应,且聚焦效应一般位于盆地中心区域,高频波入射时,地表主方向位移出现波峰波谷交错现象;次方向位移出现两点聚焦效应。

(3) 位移频谱分析表明,沉积盆地地表主方向位移,随着入射波频率增大,位移频谱曲线震荡越剧烈,且随着水平距离越近,位移幅值频谱值也基本越大。在较低频率时,地表不同点位的主方向位移幅值基本相同;在较高频率域内,地表不同点位的位移频谱特性差别很大。地表不同点位处,第一阶峰值频率均在η=1.0附近,且不同膨胀波源水平位置下,第一阶峰值频率基本一致,即位移“共振”频率基本相同。

(4) 本文结果与相应平面波结果对比发现地表位移幅值一般小于平面波入射情况,例如η=2.0,平面波入射时地表位移幅值为9.8,而球面波入射时地表位移幅值为7.6。