基于四层钻孔模型的体应变潮汐因子差异性原因分析

田 韬, 冯志生, 王 维, 叶碧文

(江苏省地震局, 江苏 南京 210014)

0 引言

钻孔体应变一般安装于地下60～100 m深度的钻孔内,利用膨胀水泥将仪器探头的测量钢筒固定在钻孔内,测量平面应变状态下钻孔的面应变[1-2]。钻孔体应变观测数据能否反映地层应力真实变化信息主要取决于探头与孔壁的耦合程度。前人多是基于三层介质耦合的钻孔受力模型,分析介质参数变化对钻孔耦合系数的影响[3-4];也有学者利用附加了垂直方向变形的三层钻孔模型,分析钻孔的垂向变形对面应变耦合系数的影响[5-7]。由于测量钢筒的长度与孔径的比大于5,观测中体应变测量钢筒轴向变形对体应变的影响可以忽略不计,采用钻孔为平面应变状态更符合观测实际[2]。利用实际观测的M2波潮汐应变波幅度与理论固体潮潮汐波幅度的比值即潮汐因子评价钻孔应变耦合状态[4,8-9],分析结果发现不同钻孔应变的潮汐因子存在明显差异,对该现象的普遍认识是钻孔耦合可能存在裂隙、偏心等因素的影响[10-12]。以前对钻孔进行应力-应变分析多是基于“钢筒-水泥层-地层”三层钻孔模型,在应力传递过程中地层被假想为半无限空间均匀各向同性介质,三层模型的局限性在于忽略了地层厚度远大于钻孔的半径,且钻孔孔壁与水泥层为两种不同力学性质的介质耦合,其中钻孔孔壁岩石弹性模量实测值远小于围岩弹性模量理论值[13],因此,三层钻孔模型中没考虑钻孔孔壁弹性模量与围岩的力学性质差异对理论计算结果的影响,该模型不能完全反映观测结果蕴含的真实物理意义。为此,田韬等[14]在三层钻孔模型的基础上提出了“钢筒-水泥环-等效弹性层-地层”四层介质钻孔耦合模型,模型中等效弹性层反映了钻孔围岩卸载效应及水泥层与孔壁或钢筒的耦合状态。本文利用该模型初步分析了我国现有钻孔体应变潮汐因子差异性的可能原因,对今后如何评价钻孔应变观测状态有一定借鉴意义。

1 四层钻孔体应变模型的潮汐因子计算

由于使用“地层-水泥环-钢筒”各向同性均匀介质三层钻孔模型对钻孔应变观测结果进行分析不能充分反映复杂环境下钻孔的实际耦合状态,为此,在三层钻孔模型中的围岩与水泥环之间增加一个等效弹性层,即“地层-等效弹性层-水泥环-钢筒”各向同性均匀介质四层钻孔模型(图1),其中等效弹性层反映钻孔围岩卸载效应及水泥层与孔壁或钢筒的耦合程度。

图1 四层介质钻孔模型结构示意图Fig.1 Structure of the four-layer medium drilling model

在均匀分布压力σ0作用下,该厚壁筒组合在平面应变状态下的物理方程[15]:

(1)

式中:ri为各层半径大小;Ei、vi为第i层介质的弹性参数。若钻孔耦合良好,在径向r2、r3、r4各接触面上,分别满足径向位移连续和径向应力连续,同时存在边界条件r=∝时,σr=σ0;r=r1时,σr=0。由以上8个边界条件,可得线性方程组如下:

(2)

由已知边界条件,方程组中8个未知参数Ai、Ci存在唯一解,依据式(1)可给出在均匀分布压力σ0作用下,钻孔面应变∑的表达式为:

(3)

式中:M是与钻孔模型参数有关的常数。

在均匀分布压力σ0作用下,假设无孔地层满足平面应力状态,地层中任一点的面应变∑′表达式为:

(4)

式中:Em、vm分别为地层的弹性模量和泊松比。

假设R为钻孔面应变∑与地层面应变∑′的比值:

(5)

定义R为钻孔面应变耦合系数,可以看出,R是各环半径和各层介质弹性参数的函数,且与均匀分布的外力σ0大小无关。

用理论应变固体潮对钻孔应变观测进行标定是目前被学者一致采用的方法[4,8]。固体地球表面的固体潮面应变理论值可以依据径向非均匀固体地球模型精确计算,假设在2阶引潮力作用下,利用固体地球模型可计算地表的半日波M2波固体潮的面应变理论值∑2[16]:

(6)

式中:h2和l2为2阶勒夫数;ρ为地球半径;g为重力;P2为月对地的2阶引潮力位。以地表面应变的固体潮理论值∑2取代地层面应变的真实值∑′及钻孔的面应变∑测量,耦合系数R可对钻孔的固体潮观测结果进行M2波调和分析获得,因此,这里耦合系数R也表示为钻孔的M2波面应变潮汐因子。

2 等效弹性层对潮汐因子理论值的影响

在日常分析中常用钻孔应变观测的潮汐因子对数据质量进行评价,因此,依据钻孔模型计算的理论潮汐因子R,可作为对钻孔应变观测结果进行分析的参考依据。为计算“地层-等效弹性层-水泥环-钢筒”四层钻孔模型中的等效弹性层弹性模量变化对潮汐因子理论值的影响,依据钻孔体应变仪器设计和安装相关资料[2],模型的参数为:钢筒内径r1=40.5 mm,钢筒外径(水泥层内径)r2=44 mm,卸载层内径(水泥层外径、井孔半径)r3=65 mm,卸载层外径(地层内径)r4=80 mm,地层外径r5=3 000 mm;钢筒弹性模量Es=210 GPa,钢筒泊松比vs=0.30,专用水泥弹性模量Ec=30 GPa,水泥、地层和等效弹性层的泊松比均为0.25(ve=vc=vm=0.25),地层弹性模量Em在25～50 GPa之间。等效弹性层的弹性模量Ee在0～Em范围内变化,Ee太小意味着钻孔等效弹性层处于疏松状态,或者水泥与孔壁或钢筒之间脱耦,或者水泥本身凝集不佳或孔壁裂隙太多以致于变的松散;Ee=Em时意味着没有等效弹性层,四层模型简化为三层。

图2为潮汐因子随钻孔弹性层等效模量Ee的变化。可以看出,地层弹性模量Em对潮汐因子的影响比较显著,地层弹性模量Em越大,对应的潮汐因子也越大;当地层弹性模量Em在15～75 GPa之间,对应的潮汐因子理论值在1.0～2.5之间;当地层弹性模量Em小于15 GPa时,对应的潮汐因子理论值小于1。当地层弹性模量不变时,等效弹性层的弹性模量越小对潮汐因子的影响越大,潮汐因子先随Ee快速增加然后逐渐变缓,随等效弹性层的弹性模量逐步增大潮汐因子出现趋于转平迹象,当等效弹性层的弹性模量等于地层的弹性模量,四层退化为三层模型,即图2中每条曲线右端。

图2 潮汐因子随等效弹性模量Ee的变化(Ec=30 GPa)Fig.2 Variation of tidal factor with the equivalent elastic modulus Ee (Ec=30 GPa)

3 现有钻孔体应变钻孔等效弹性层等效弹性模量的估算

本文共收集了中国大陆正在运行观测的24套花岗岩类和23套灰岩或砂岩类基岩的钻孔TJ-2C型体应变观测资料(表1、表2)。TJ-2C型体应变仪器探头总长度1.3 m,探头感应筒筒长0.5 m,内径(半径)0.040 5 m外径(半径)0.044 m,采样率1次/min,分辨率1×10-9,动态范围±1×104,钻孔直径0.130 m,钻孔深度60～100 m,中间使用专用水泥加石英砂填充耦合[2]。

M2波潮汐因子可利用软件MAPSIS[17]对观测资料的整点值时间序列进行调和分析获得,表1和表2给出了这些钻孔的M2波潮汐因子观测结果。由表1可见,钻孔地层岩性为花岗岩类的潮汐因子值最大的为1.86、最小的为0.01,其均值约为0.83,方差为0.33,潮汐因子大于1的台站有9个,占总数的37.5%,潮汐因子小于0.50的台站有7个,占总数的29%。由表2可见钻孔地层岩性为灰岩或砂岩类的潮汐因子值最大的为1.39、最小的为0.01,其均值约为0.57,方差为0.17,潮汐因子大于1的台站有5个,占总数的21.7%,潮汐因子小于0.50的台站有12个占总数的52.2%。对比表1和表2的潮汐因子最大值和均值,发现我国现有钻孔体应变潮汐因子基本反应钻孔地层岩性,即岩性较硬的花岗岩类弹性模量大,潮汐因子也大,岩性较软的灰岩或砂岩类弹性模量小,潮汐因子小。

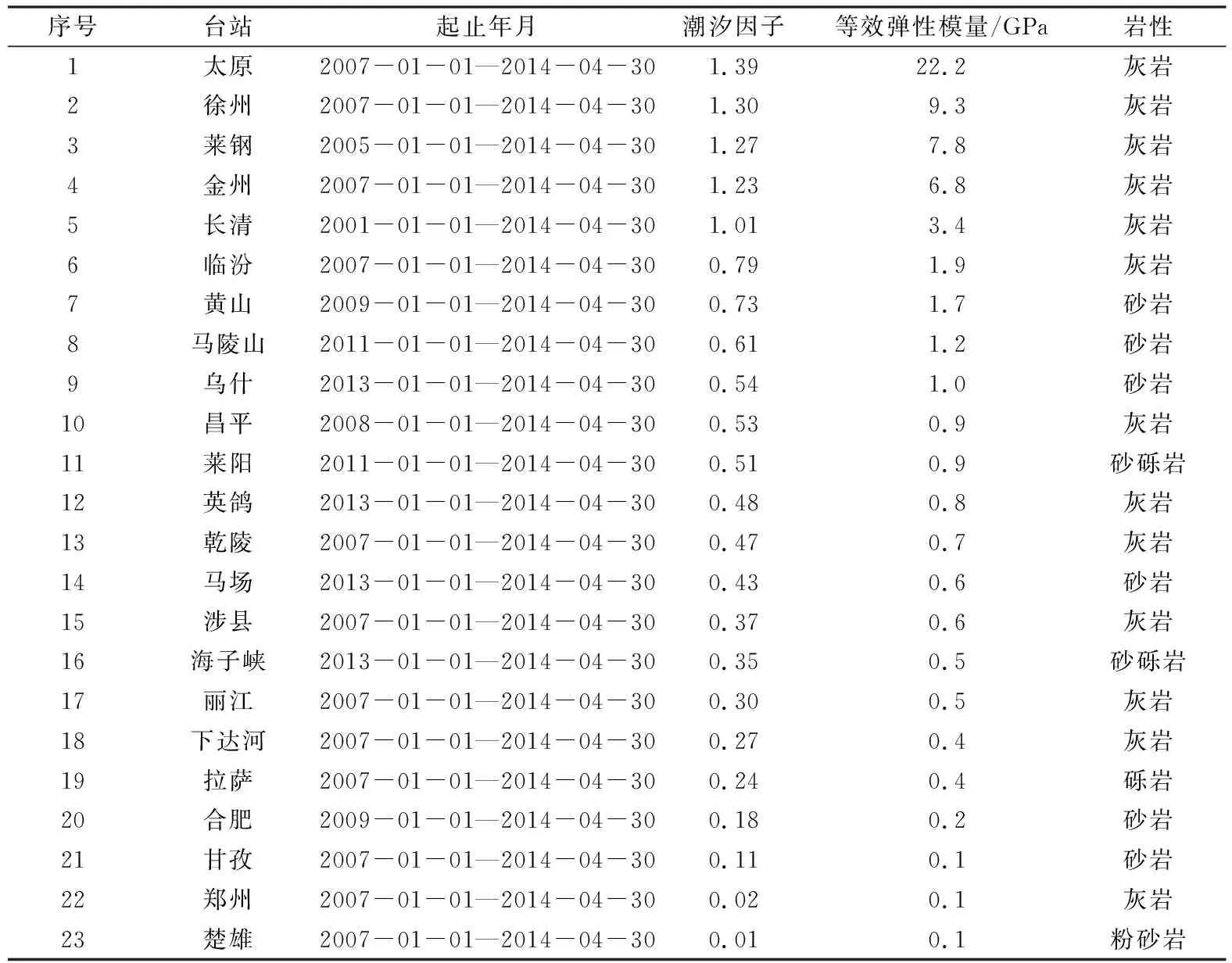
表2 灰岩或砂岩类钻孔的面应变潮汐因子观测值

由表1和表2可以发现,我国现有钻孔体应变的潮汐因子差异性很大,即使地层岩性一样也是如此,显然不能用地层岩性弹性模量的差异性来解释,为此我们取花岗岩类弹性模量Em=50 GPa,灰岩或砂岩类弹性模量Em=25 GPa,分别给出其理论潮汐因子随等效弹性层弹性模量的变化,及据此给出各钻孔体应变的等效弹性模量(表1、表2、图3)。

图3为两类地层中钻孔体应变潮汐因子随等效弹性层弹性模量变化,其中曲线上四角为岩性较硬的花岗岩类钻孔观测到的M2波潮汐因子,圆圈为岩性较软的灰岩或砂岩类钻孔观测的M2波潮汐因子在曲线上的投影。

岩石的弹性模量随外界环境的不同其大小也不相同,一些主要岩石的杨氏模量[18]:花岗岩为26～69 GPa、片麻岩为20～59 GPa、砂岩为5～80 GPa、灰岩为10～79 GPa。由表1和表2及图3可以发现,无论基岩为岩性较硬的花岗岩类,还是岩性较软的灰岩或砂岩类,其等效弹性层的弹性模量都小于10 GPa,即所有钻孔均存在其等效弹性层的弹性模量远小于地层弹性模量的现象。

等效弹性模量的大小反映了钻孔的耦合状态,我们以砂岩弹性模量最小值5 GPa小一个数量级0.5 GPa作为判定钻孔耦合状态的下限,即等效弹性模量低于0.5 GPa时认为钻孔脱耦,则由表1和表2可以发现,花岗岩类钻孔共有7个台站的等效弹性模量低于0.5 GPa,占29%;灰岩或砂岩类钻孔共有7个台站的等效弹性模量低于0.5 GPa,占30%。很显然,若以等效弹性模量低于0.5 GPa为标准确定该钻孔为脱耦,则以上这些钻孔数据是无法用于地震监测预报。

图3 两类地层中潮汐因子随等效弹性模量Ee的变化(Ec=30 GPa)Fig.3 Variation of tidal factor with the equivalent elastic modulus Ee in two kinds of strata (Ec=30 GPa)

4 讨论与结论

本文基于“地层-等效弹性层-水泥环-钢筒”四层介质耦合钻孔模型,初步分析了我国现有地层岩性为花岗岩类和灰岩或砂岩类钻孔体应变潮汐因子与等效弹性层弹性模量的关系,发现:

(1) 无论是基岩岩性为岩性较硬的花岗岩类,还是岩性较软的灰岩或砂岩类,其等效弹性层的弹性模量都小于10 GPa,即均存在钻孔等效弹性层的弹性模量远小于地层弹性模量的现象,因此,钻孔潮汐因子低的原因可能是等效弹性层弹性模量较低所致;

(2) 等效弹性模量的大小反映了钻孔的耦合状态,若以砂岩弹性模量最小值5 GPa小一个数量级即0.5 GPa作为判定钻孔耦合状态的下限,即认为等效弹性模量低于0.5 GPa时认为钻孔脱耦,则统计表明我国现有钻孔体应变有约30%的钻孔体应处于脱耦状态,这一研究结果对预报人员应用这些钻孔资料开展地震分析预报工作有重要指导意义。