复值耦合神经网络的渐近和有限时间聚同步
2021-03-30李梦月李必文
李梦月,李必文
(湖北师范大学 数学与统计学院,湖北 黄石 435002)
0 引言
自Pecora L M和Carroll T L[1]引入混沌同步以来,同步在神经网络方面的研究已然成为一个热门的课题。聚同步即属于同一个集群的个体完全同步,来自不同集群的个体不同步。作为一种更复杂的同步模式,近年来对于它的研究已涉及到了很多领域,如万维网络、电网网络和细胞神经网络等[2,3]。Cao Jinde等人[4]研究了具有时滞的混合耦合神经网络的聚同步问题,通过构造特殊的耦合矩阵,提出了实现聚同步的新方法。文献[5]讨论了复杂网络在有限时间的随机同步问题,利用有限时间稳定性理论和不等式技巧,得到了保证复杂网络在有限时间内实现随机同步的充分条件。Liu Peng等人[6]从整数阶的集群同步拓展到分数阶,研究了具有时滞的分数阶耦合神经网络的渐近和有限时间聚同步问题,通过引入分数阶微分系统的稳定性理论和Filippov正则化框架,得到了实现分数阶耦合神经网络渐近和有限时间聚同步的充分条件。更多的结果可参看文献[7~10]。值得注意的是这些研究主要是实值神经网络。
在大量的实际应用中,复信号经常出现,实值网络不易解决此类问题,因此对复值网络的研究变得极为重要。在各领域研究者的不懈努力与探索下,复值神经网络已基本建立,并且在众多领域有着广泛的应用,如联想记忆、图像处理和通信[11~14]等。复值神经网络作为实值神经网络的一种扩展,它有更复杂的状态,权值矩阵,激活函数等。它能解决更为复杂的问题,如单一实值神经元无法解决的XOR问题和探测对称问题。从而对复值神经网络的动力学研究是十分重要的,目前对复值神经网络的研究包括平衡点的存在唯一性[15]、各种稳定性问题[16~21]和各种同步问题等。值得注意的是,虽然近年来对复值神经网络的同步问题已有不少研究,如文献[22]研究了具有离散和分布式的两个加性时变时滞的复值神经网络的同步,并基于矩阵不等式和倒凸方法,得到了确定复值神经网络主从全局同步的准则。Chen jie jie等人[23]研究了具有时滞的分数阶复值忆阻神经网络的全局渐近稳定和自适应最终Mittag-Leffler同步。在文献[24]中,Zhang wei wei等人通过构造合适的Lyapunov函数,利用分数阶比较原理,建立了具有遗漏时滞分数阶复值神经网络同步的一些准则等。但是关于复值神经网络聚同步这方面的研究还比较少。
在实际生活中时滞几乎是无法避免的,尤其是在信号传输的过程中,由于放大器的切换速度有限,神经网络不可避免的会有延迟,这会给神经网络造成震荡、分岔、不稳定等问题,从而影响神经网络的动力学行为,因此讨论具有时滞神经网络的动力学行为十分重要。
基于以上讨论,本文的目的旨在研究具有时变时滞的复值耦合神经网络的聚同步问题。利用Halanay不等式,Filippov解的框架和微分包含原理,得到了复值耦合神经网络在相应控制策略下实现渐近和有限时间聚同步的充分条件。本文余下部分组织如下,第一节是对本文符号进行说明和模型的描述。第二节给出了本文的主要结果。在第三节中用两个数值例子说明了我们所得结果的有效性。最后一节给出结论。
1 准备工作
1.1 符号说明
C([t0-τ,t0],n)表示具有一致收敛拓扑的从区间[t0-τ,t0]到n连续函数的Banach空间。QR和QI分别表示矩阵Q∈m×n的实部和虚部。
1.2 模型描述
用Ω={N,ε,G}表示有节点集N={1,2,…,N}(∈+,N>2),边集ε⊆N×N和耦合矩阵
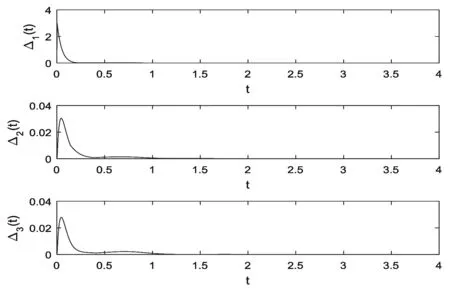
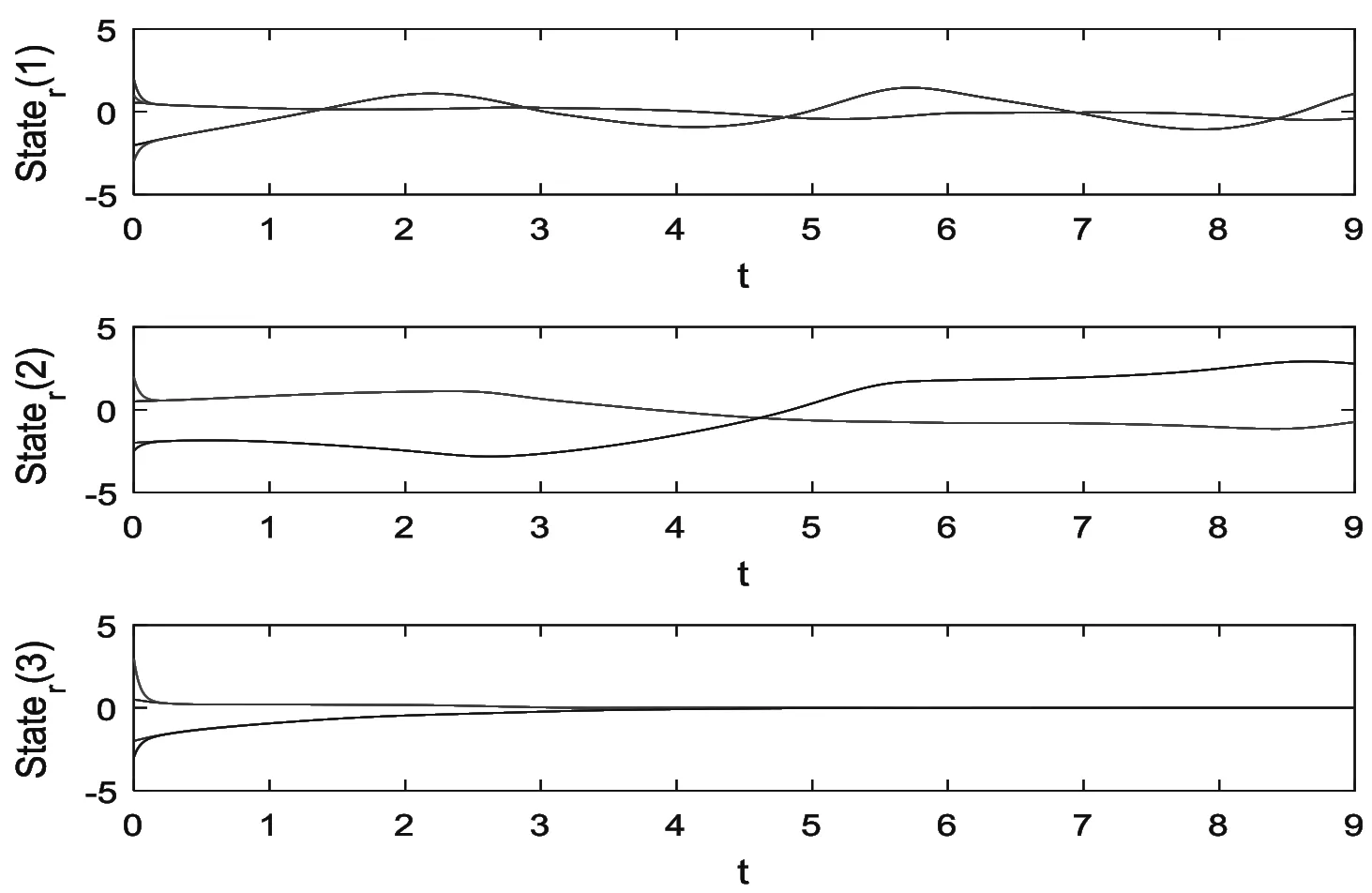
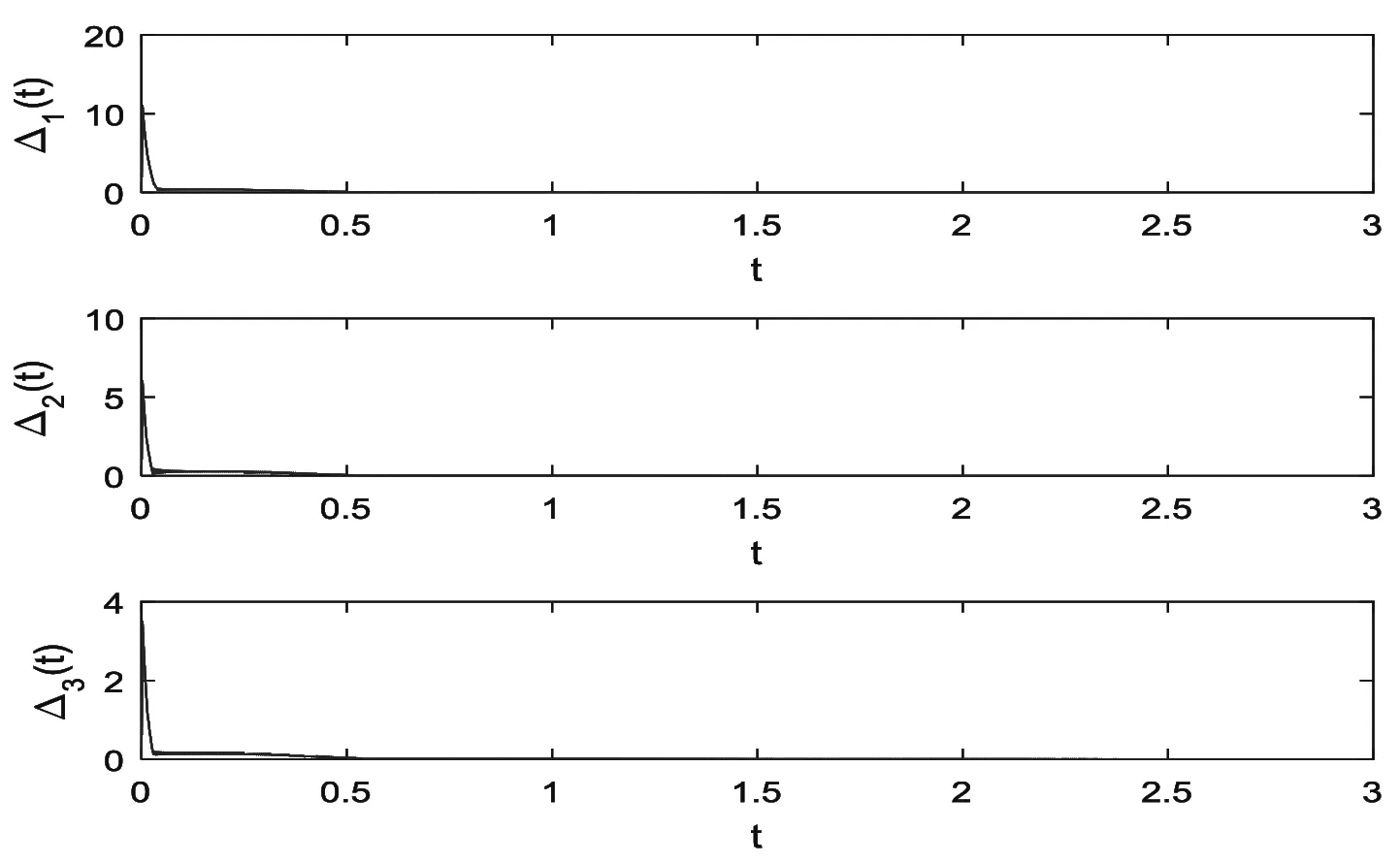
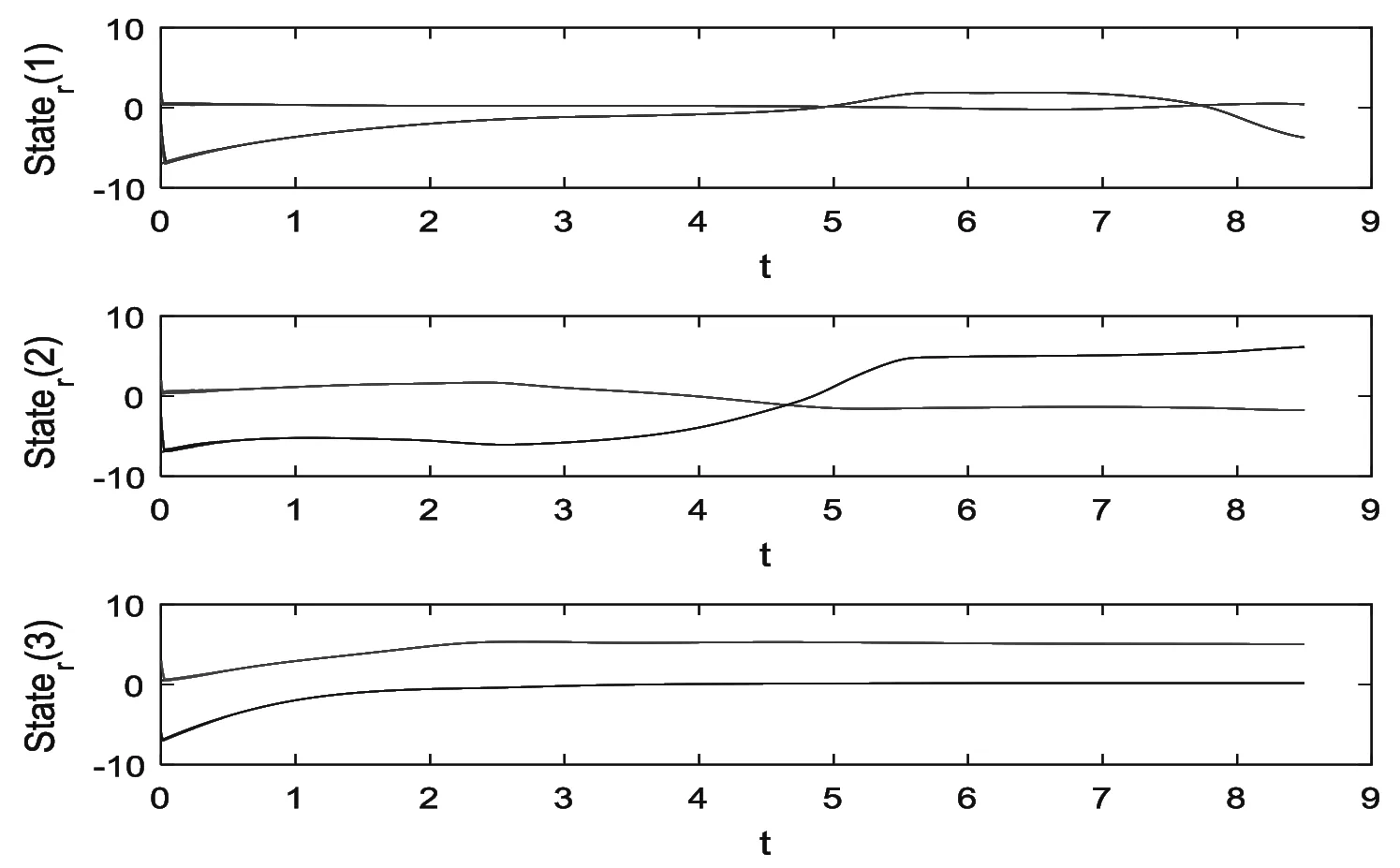
G=[gsj]N×N∈N×N的图,这里的gsj满足:对于任意的s=1,…,N有如果从第s个节点到第j个节点间有连接,则gsj>0,否则gsj=0.用{W1,W2,…,WM}表示具有M(2≤M 考虑由N个复值神经网络构成的耦合系统,第s个复值神经网络的动态方程可描述为: (1) 这里的zs(t)=(zs1(t),zs2(t),…,zsn(t))T∈n表示第s个复值神经网络在t时刻的状态向量; f(zs(t))=(f1(zs1(t)),f2(zs2(t)),…,fn(zsn(t)))T∶n→n表示神经元的激活函数;τ(t)是时变传输时滞且满足n表示外部输入;us(t)是被设计的控制器。 在本文中,我们假设(1)中的激活函数满足如下所给假设条件: 假设2 令w=w1+iw2,其中w1,w2∈.fm(w)可由它的实部和虚部表示为: 基于以上假设,现令zs(t)=xs(t)+iys(t),其中xs(t),ys(t)∈n则复值神经网络(1)可改写为如下形式: (2) 将其写成如下更紧凑的形式: (3) 这里 F1(ps(t))=((fR(xs(t)))T,(fR(xs(t)))T)T F2(ps(t))=((fI(ys(t)))T,(fI(ys(t)))T)T 系统(3)的初始条件如下: (4) 则复值神经网络(1)能够以有限时间t1实现集群{W1,W2,…,WM}的聚同步。这里的rk(t)表示第k个集群所有节点的相同局部动态。它可能是第k个集群中的平衡点,周期轨道或者是一个混沌吸引子,且满足如下微分方程: (5) 类似地,把该复值神经网络分解为实部和虚部,则(5)可改写为如下形式: (6) 其中 假设3 假设耦合矩阵G满足 其中Gkk∈(lk-lk-1)×(lk-lk-1)是一个具有非对角元素非负的零行和矩阵,Gkr∈(lk-lk-1)×(lr-lr-1)(k≠r)是零行和矩阵,k,r=1,2,…,M. 结合假设3和(5)式,对于任意的s∈Wk,k=1,2,…,M,有下式成立: (7) 在推导本文的结果前,先给出下面几个非常有用的引理。 引理1[25]如果存在常数k1>k2>0,使得定义在[t0-τ,+∞)上的非负连续函数y(t)满足如下不等式: h→0+表示h从右边趋向于0. 引理2 假设V(t)是非负连续函数,如果 D+V(t)≤μ1V(t)+μ2∀t≥t0 其中μ1≠0和μ2为常数,则对于任意的t≥t0,有下式成立: V(t)≤(V(t0)+μ2/μ1)eμ1(t-t0)-μ2/μ1 证明 在不等式D+V(t)≤μ1V(t)+μ2两边同乘e-μ1(t-t0),则有D+(e-μ1(t-t0)V(t))≤μ2e-μ1(t-t0),接着对该不等式左右两边从t0到t积分,即可得到V(t)≤(V(t0)+μ2/μ1)eμ1(t-t0)-μ2/μ1. 在这节中,给出了复值耦合神经网络(1)渐近和有限时间聚同步的判据。 令es(t)=ps(t)-qk(t),s∈Wk,控制器设计如下: (8) 根据(3)(6)(7)和假设1,误差动力系统可以描述为: (9) 基于以上准备,得到如下结果: (10) 构造如下非负函数 下面计算V(t)沿着系统(9)方向的右上Dini导数 (12) 这里的sgn(es(t))=(sgn(es1(t)),sgn(es2(t)),…,sgn(es,2n(t)))T∈2n, 显然 (13) (14) 类似地,令 可以得到 (15) (16) 和 (17) 另一方面,有如下不等式成立 (18) 利用耦合矩阵G的性质,我们可以得到 和 然后结合(18)式可得如下不等式 (19) 接着,依次结合不等式(13)(14)(15)(16)和(17)得到不等式: ≤-aminV(t)+bmaxV(t-τ(t)) 这里的 定理证明完毕。 由于设计的控制规律us(t)是不连续的,因此系统(1)的解不能用常规意义下的解来定义。为了得到系统(1)的解,下面考虑Filippov意义下的解。 首先介绍关于集值映射的定义。对于任意的E⊂n,令 ER={Re(z)∶z∈E}EI={Im(z)∶z∈E} 假设E⊂n,称z→F(z)是由E到n的集值映射,如果对任意z∈E,存在非空集合F(z)⊂n. 由文献[23],我们可以定义系统(1)的Filippov解,如果z(t)在[t0,∞)的任意紧区间上绝对连续且满足微分包含: (20) 则称复值函数z(t)是系统(1)在[t0,∞)上满足初值条件下的一个Filippov解,其中K[us(t)]表示us(t)的凸闭包。控制规律如下: (21) 令us(t)的集值映射为: 其中 将系统(1)分解为实部和虚部,则其微分包含可表示为 根据(5)(6)(7),假设1和微分包含原理,可得对于任意的t≥t0,误差系统满足下式 (22) (23) 另外可得 (24) (25) 最后将(23)式和(13)(14)(15)(19)和(25)式结合,有下面不等式成立 (26) 根据引理2,V(t)≤(V(t0)+)e-η(t-t0)-,这里的令 (27) 下证对于所有t≥T1,有V(t)=0成立。 作为定理2的一个特殊的情况,有如下结果成立: (28) 这节中,我们将给出几个数值例子来阐述该文章的主要结果。 例1 考虑二维复值神经网络(1),对于任意的zsj=xsj+iysj,其中xsj,ysj∈,激活函数满足 对于任意的t∈[-1,0],rk=(0.5+0.8i,-2-3i)T,k=1,2,3.给定复值耦合神经网络(1)的耦合矩阵如下 且系统(1)分为三个集群W1={1,2,3},W2={4,5},W3={6,7}.基于以上陈述,可得 (29) 通过计算可得: 这是一个非奇异M-矩阵。根据定理1,系统(1)在控制器(29)下能够实现渐近聚同步。在模拟中,对于任意t∈[-1,0],令z1(t)=z4(t)=z6(t)=(0.5+0.8i,-2-3i)T,并且 zs(t)=(xs1+iys1,xs2+iys2)Ts=2,3,5,7 图1 控制器(29)下的实部同步误差轨迹 图2 控制器(29)下的虚部同步误差轨迹 由图3和图4也可看出所有状态实现渐近聚同步。 图3 控制器(29)下集群W1,W2,和W3的实部状态图 图4 控制器(29)下集群W1,W2和W3的虚部状态图 (30) 并令 通过计算可得 根据定理2,系统(1)在控制器(30)下可以在有限时间实现聚同步,另外对于任意t∈[-1,0],令z1(t)=z4(t)=z6(t)=(0.5+0.8i,-7-8i)T,zs(t)的实部和虚部同例1是从[-10,10]中随机产生的,其中s=2,3,5,7,于是可得这个同步时间估计值T1=16.8501.图5和图6可看出系统t≤2在同步,另外图7和图8也能明显看出所有状态在有限时间内实现了聚同步。这表明实际同步时间可能远小于理论获得值T1.这是因为定理2中T1是同步时间的上确界。因此找到有限时间同步更精确的上确界是一个值得探讨的问题。 图5 控制器(30)下的实部同步误差轨迹 图7 控制器(30)下集群W1,W2和W3的实部状态图 图8 控制器(30)下集群W1,W2和W3的虚部状态图 本文主要讨论了具有时变时滞的复值耦合神经网络的渐近和有限时间聚同步的问题。在处理复值耦合神经网络问题上采用实部虚部分离的方法。基于Halanay不等式理论得到了复值耦合神经网络实现渐近聚同步的充分条件。基于Filippov解的框架和微分包含原理给出了复值耦合神经网络在不连续控制规律下实现有限时间聚同步的准则,并推导出了同步时间的上确界。有限时间聚同步更精确的上确界是进一步可探讨研究的问题。另外将渐近聚同步问题中的控制器设计为脉冲控制器或基于事件触发的脉冲控制器也是我们下一步考虑研究的方向。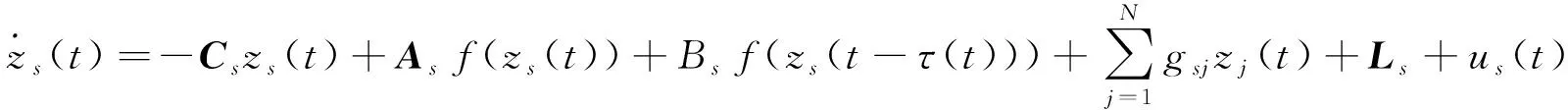
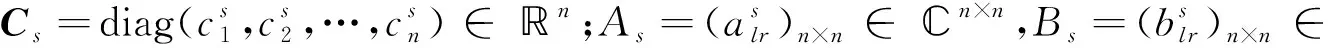
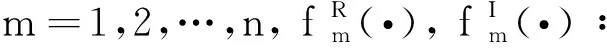

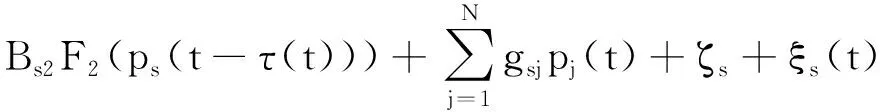
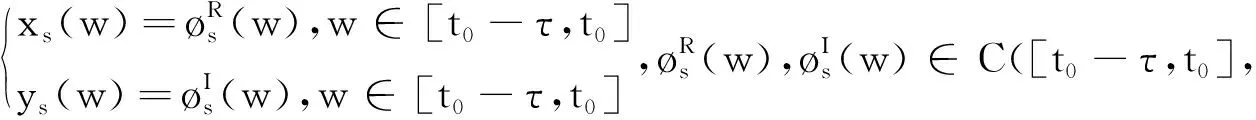

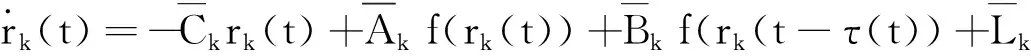

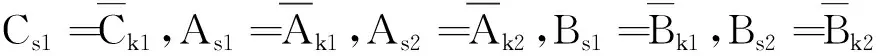

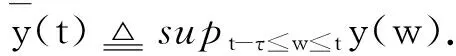
2 主要结果
2.1 渐近聚同步
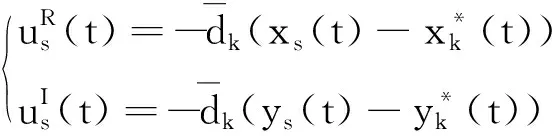
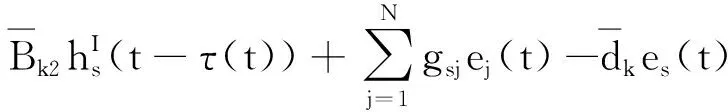
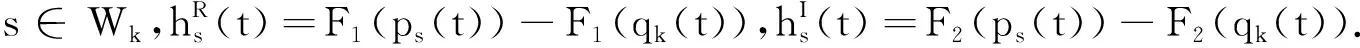
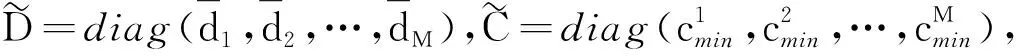
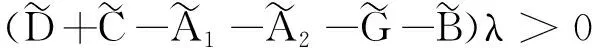
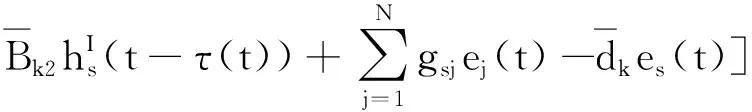
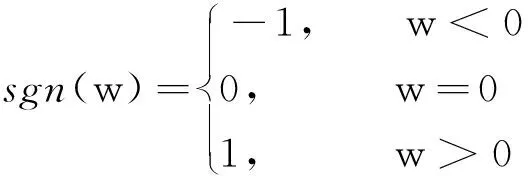
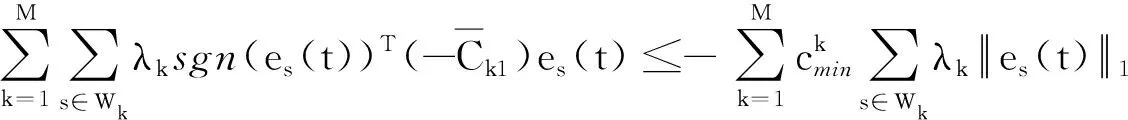
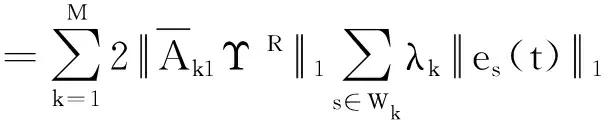
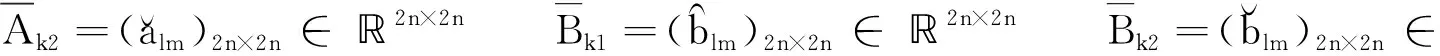
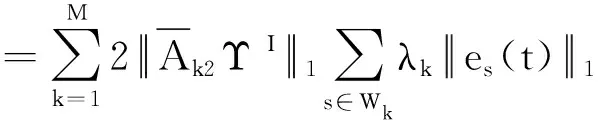

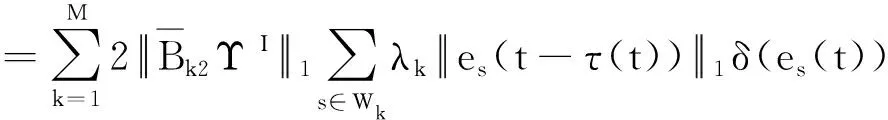

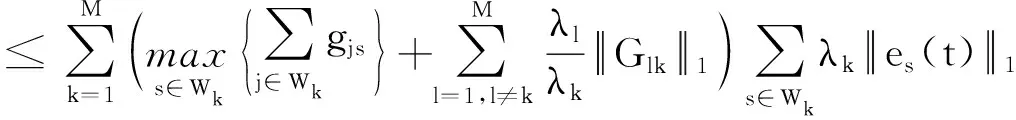
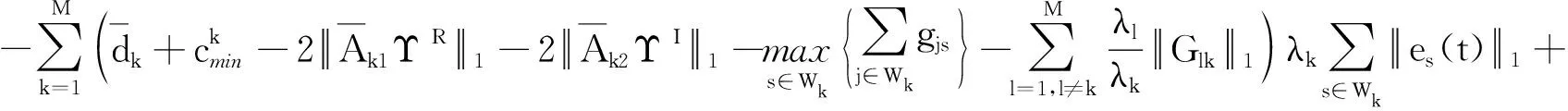
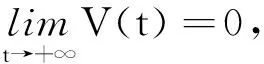
2.2 有限时间聚同步
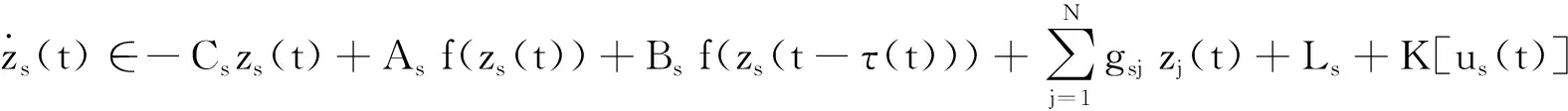
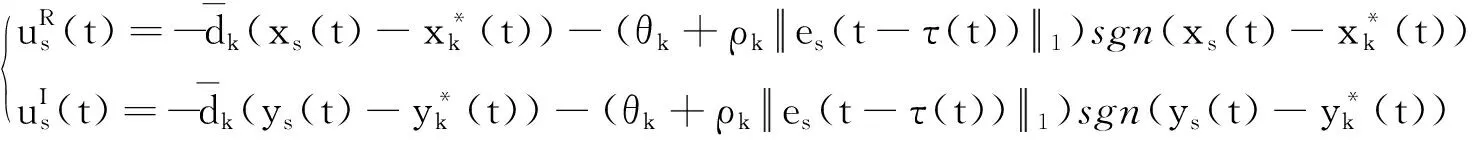

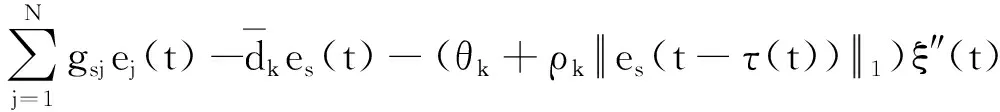
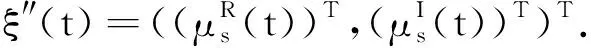

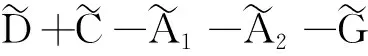
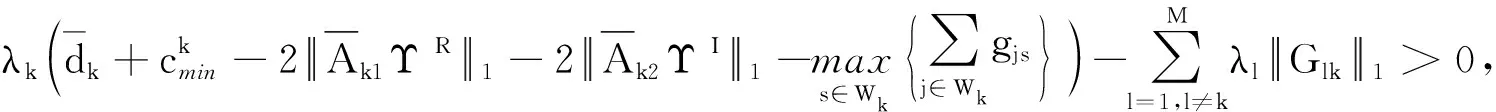
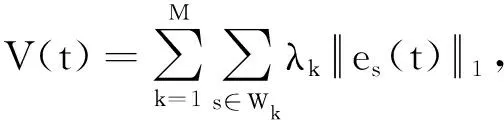
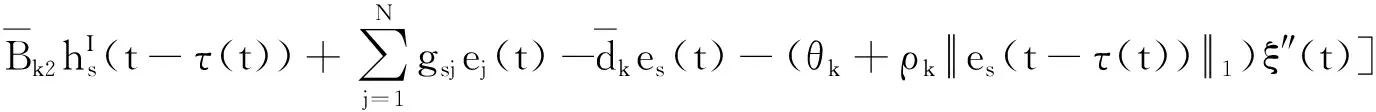
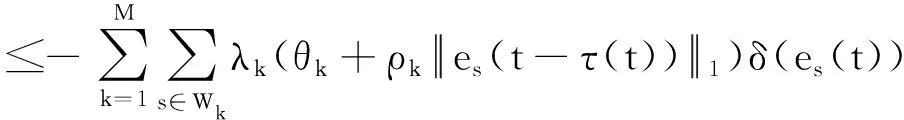


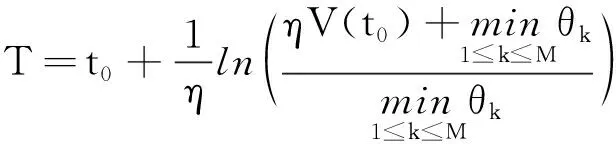
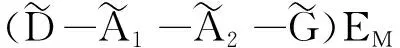
3 数值模拟


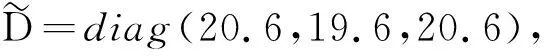
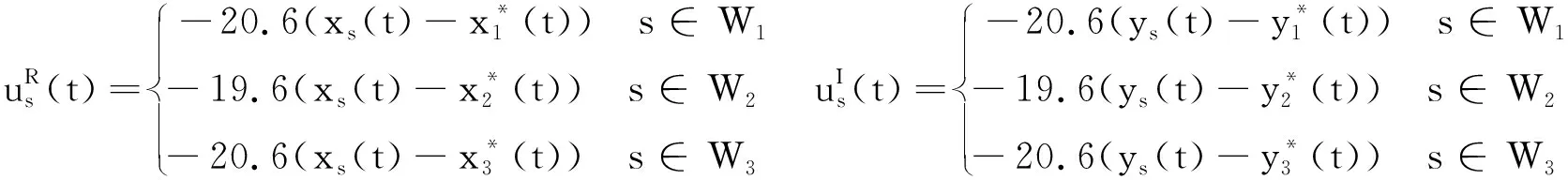
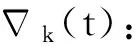
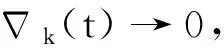
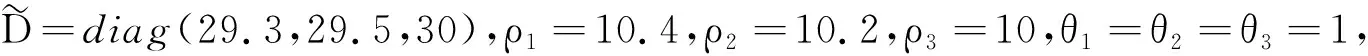
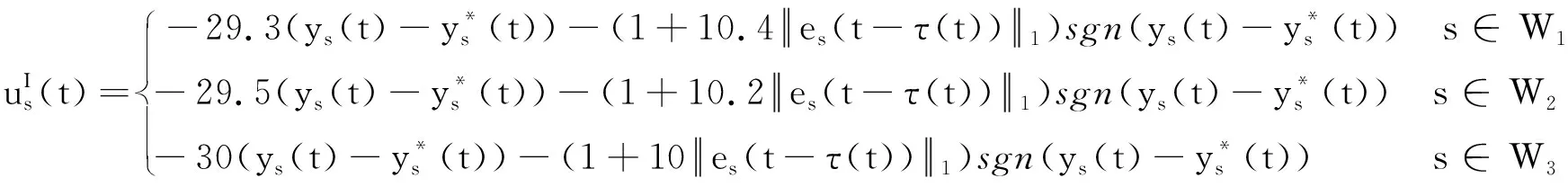
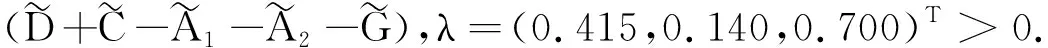
4 结论
