机械振动和地震激励下的风电基础动力仿真

徐腾飞，张圣东，游世辉

（1.枣庄市船舶检验中心，枣庄277400；2.枣庄学院 机电工程学院，枣庄277000）

0 引言

风能是近期内最具大规模开发利用价值的可再生能源，而目前风能利用最直接的方式就是风力发电［1］.在强震作用下，可能会引起风电塔的倒塌等其他形式的破坏.风电机组运行时产生的机械振动激励也对其寿命有相当大的影响.因此探索风电基础在机械振动激励和地震激励作用下的动力响应具有重大意义.有限元法是目前研究风力发电机动力响应使用较多的方法之一.在有限元分析方面，柳国环等［2］用数值模拟方法研究了在强地震作用下的海上风电结构响应.沈华等［3］基于风电塔低阻尼特性建立了在不同设计使用期的地震作用计算模型.在模态分析方面，靳军伟等［4］研究了风电系统各部分参数对风电基础模态的影响程度.韩花丽等［5］提出了结合激励荷载的性质、基于风电自身特征的模态振动分析，修正地震效应的叠加方法，并将其应用于风电的地震作用动力分析计算.

本文对风电基础的动力学参数进行了求解.并用振动分析的计算方法，基于Matlab/Simulink数学软件，对风电基础在机械振动激励和地震激励作用下的动力响应分别进行了分析，得出相关的位移、速度和加速度时程曲线，并探讨了不同动力学参数及不同类型地震波对风电基础动力响应的影响，为后续风电的安全性设计提供一定的参考.

1 风力发电机基础的动力学参数计算

1.1 地基阻尼系数的计算

假设基础振动引起的波动在基础底面呈平面波形状，如图1所示.

图1 垂直振动的波动逸散图

式中，uz0为基础板位移振幅，ρ为质量密度，为地基纵波波速；λ，G为拉梅常数.

基础与地基接触面上的应力为

基础板振动速度为

设基础板底面积为A，则基础与地基接触面上的波动反力为

由此可得，基础逸散阻尼力与基础板振动速度u˙z0成正比，其系数ρVpA即为垂直振动时等效黏性阻尼系数

1.2 矩形地基刚度的计算

圆形地基的刚度理论计算已有较多研究，本文在Sung的研究基础上研究了解析法求解矩形基础-地基刚度和阻尼系数［6］，原理与圆形表面基础地基刚度的计算相同.本节用基底应力分布有限元方法进行验证，将结果与Sung论研究进行比较.

1.2.1 风力电基础静刚度分析

风力电基础为矩形扩展基础，分三层，每层高1 m，底层长为12 m，宽为8 m，顶层长为4 m，宽为3 m.埋于地下，风力发电机上部质量为2000 t，均匀作用在基础顶部.定义地基为同一类型土，地基土为一上表面以基础顶部中心为中心的长方体，长方体长和宽都为48 m，高10 m.本文考虑C15混凝土基础-碎石土地基和C25混凝土基础-碎石土地基另种组合，其相关力学参数如表1和表2所示.

表1 混凝土的弹性模量、泊松比和密度参考值

表2 地基（土）的弹性模量和泊松比参考值

为求解基底土反力分布，我们取过基础底面长边方向上某一条直线为计算路径，并对模型顶部加载均布力15915 N/m2，固定土层的前后左右及底面五个面.

由地基刚度计算方法，通过ANSYS导出基底反力曲线图，如图2和图4所示.并将反力数据导入OriginPro软件，可以求得地基静刚度系数与位移的曲线，如图3和图5所示：

图2 C15基底反力曲线图

图3 C15基础刚度位移曲线图

图4 C25基底反力曲线图

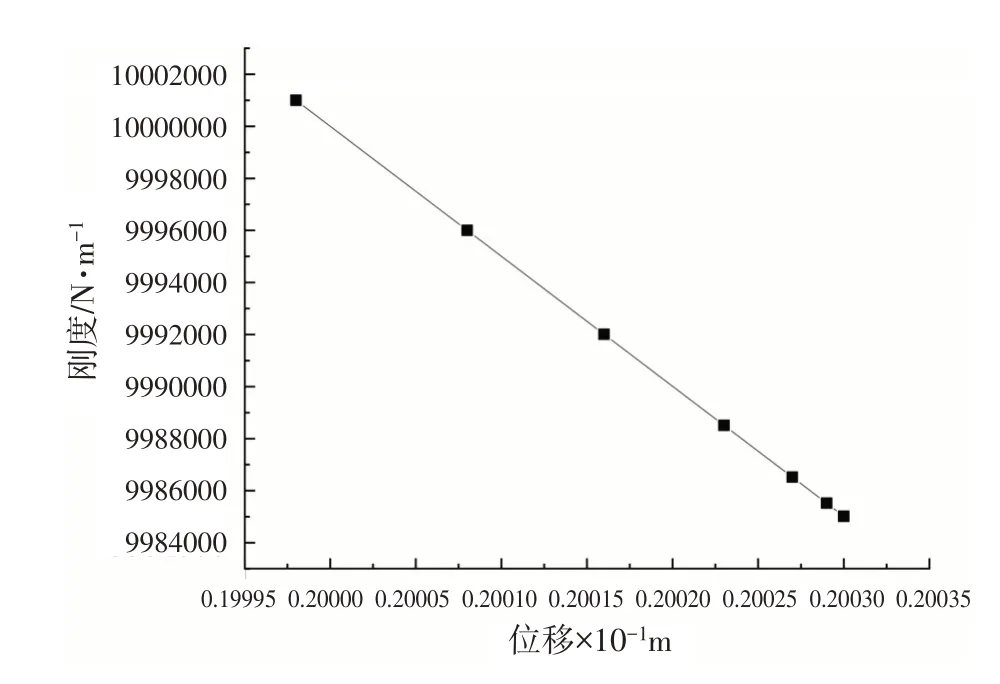
图5 C25基础刚度位移曲线图

由上述组图可以看出，土反力曲线基本为抛物线形状，这与Sung的土反力理论假设基本符合.同时，基础底板的刚度虽然有些呈递增趋势，有些呈递减趋势，但两者的趋势都与理论相符.

1.2.2 风电基础的动刚度分析

在基础顶部作用垂直动荷载20 t，持续时间为1 s，取过基础底面长边方向上的某一条直线为计算路径，固定土层的前后左右及底面五个面，最后用ANSYS求解，取0.75 s时得到的结果.

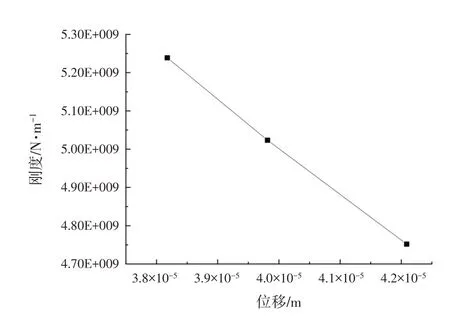
图6 C15基础刚度位移曲线图

图7 C25基础刚度位移曲线图

在垂直动荷载的作用下，同一时刻、同一路径上基础底板的刚度有随着基础底板位移的增大而减小，也有随着基础底板位移的减小而增大.这两种趋势与垂直静力作用下基础底板刚度的变化是一致的.也就是说在这一时刻，这一变化与Sung的假设理论是相符的.

风电基础受机械振动激励和地震激励时的动力学方程可表示为：

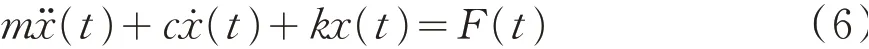
式中m为质量，c为阻尼，k为刚度，x¨(t)、x˙(t)、x(t)分别为结构的加速度、速度和位移.F（t）为简谐激励力或随机力.

2.1 机械振动激励作用下的风电基础响应

某风电厂制造的GW87/1500大型风力发电机总质量约193188 kg，额定功率1500 kW，转轮直径88 m，轮毂高度70 m.叶轮直径3.73 m，高4.875 m，叶轮重量13850 kg，单根叶片长度43 m，单根叶片重量6400 kg，一台风力发电机通常有3根叶片.切入风速3 m/s，额定风速10 m/s，切出风速22 m/s，最大安全风速52.5 m/s，其发电机的额定功率1580 kW，额定转速20.5 r/min，并网转速10.6 r/min.以额定转速得到工作时的角速度约为2.16 rad/s，对质量配平过的风轮需要考虑0.005R的质量偏心距，则本例中的偏心距约为0.44 m，风电基础所受的机械振动简谐激励力为64847.2sin2.16t N.多孔砂岩的刚度系数为400 kN/m.本文计算案例风电基础为混凝土材料，刚度取500 kN/m，本文设黏性阻尼系数为0.2，质量约330000 kg，取样时间30 s.

图8 风电基础位移时程曲线图

图9 风电基础速度时程曲线图

图10 风电基础加速度时程曲线图

由图8～图10可得风电基础的位移最大值为5.3919×10-7m，最小值为-5.4192×10-7m；速度的最大值为8.3232×10-7m/s，最小值为-8.3196×10-7m/s；加速度的最大值为1.41×10-6m/s2，最小值为-1.41×10-6m/s2.

2.2 地震激励作用下的风电基础响应

目前通用的三种强震记录，分别选用El-centro地震波，1940年监测，震级为7.1级，时间间隔0.02 s，持续时间54 s，加速度峰值341.7 cm/s2，南北方向，适用于中软场地.天津地震波，1976年监测，震级6.9级，时间间隔0.01 s，持续时间19.20 s，加速度峰值147 cm/s2，适用于软弱场地，天津波相对比较安全，南北向常用.Taft地震波，1952年监测，震级为7.4级，时间间隔0.02 s，持续时间35.2 s，加速度峰值152.7 cm/s2，上下方向，适用于中硬场地.本文以天津波作用于风电基础得到其图像和时程曲线分别如下：

图11 天津地震波图像

图12 风电基础位移时程曲线图

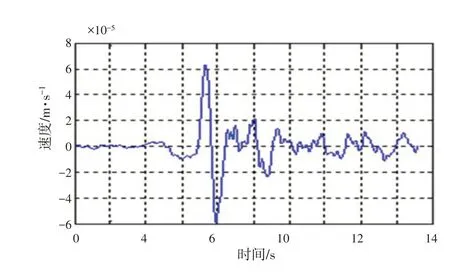
图13 风电基础速度时程曲线图

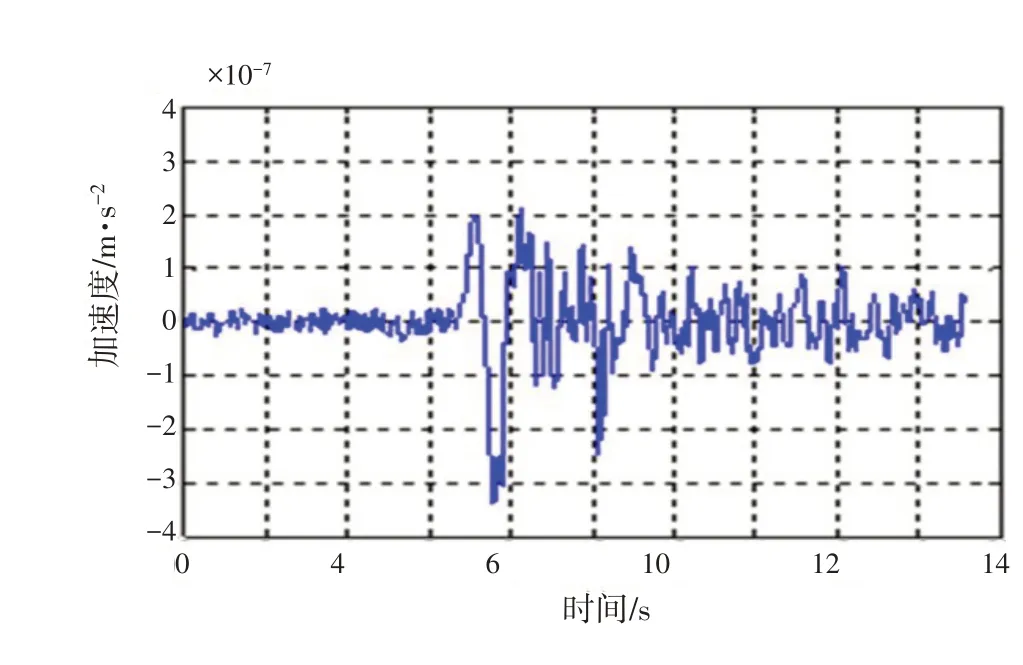
图14 风电基础加速度时程曲线图

由图11～图14可得风电基础发生的位移最大值为1.8568×10-5m，最小值为-8.517×10-6m；速度最大值为6.3114×10-5m/s，最小值为-5.9503×10-5m/s；加速度最大值为5.0371×10-7m/s2，最小值为5.0371×10-7m/s2.

3.1 阻尼对风电基础动力响应的影响

本节仅选取El-centro地震波作用下的风电基础的时程响应曲线作为对比，质量330000 kg，刚度500 kN/m.改变黏性阻尼系数的大小，单位N/s·m.图15（a）、图15（b）、图15（c）、图15（d）分别是黏性阻尼系数C为0.1、0.2、0.3、0.4时风电基础的位移时程曲线图.

图15 风电基础的位移时程曲线图

通过多次改变黏性阻尼系数C的值（0＜C＜1），发现同等条件下，不论如何改变C的值，其位移，速度和加速度的时程响应曲线都基本不变.

3.2 刚度对风电基础动力响应的影响

本节仅选取Taft地震波作用下的风电基础时程响应曲线作为对比，风电基础质量330000kg，黏性阻尼系数阻尼为0.2，改变刚度的大小，单位为kN/m.图16（a）、图16（b）、图16（c）、图16（d）分别是k为300、400、500、700时的风电基础位移时程曲线图.

图16 风电基础位移时程曲线图

在k=300kN/m时位移的最大值为2.5121×10-8m，最小值为-2.5942×10-8m；在k=400kN/m时位移的最大值为37750×10-8m，最小值为-3.9917×10-8m.在k=500kN/m位移最大值为3.1485×10-8m，最小值为-3.6499×10-8m，在k=700kN/m时位移的最大值为4.1162×10-8m，最小值为-4.5071×10-8m.由以上结果可明显得出，质量和黏性阻尼系数一定时，一定范围内，刚度增加，则位移随之增大.

4 结论

本文基于有限元软件ANSYS对风电基础的动力学参数进行了计算，采用理论分析和数值模拟相结合的方法来对风电基础受机械振动激励和地震激励的动力响应进行了初步研究，并基于Simulink软件对风电基础在不同激励下的动力响应进行数值模拟，得出了结构的加速度、速度、位移时程曲线.并对动力学参数对其最终动力响应的影响程度进行研究.

（1）本文基于理想的模型与约束条件下，基于有限元软件ANSYS对风电基础的动力学参数进行简要计算，就某一时刻而言，动力作用下的结果与静力作用时是一致的.

（2）风电基础在机械振动激励下的响应是瞬态响应和稳态响应综合的结果，若机械激励持续不断，风电基础的振动也不会停止，随着激励响应达到一个稳态平衡状态.在刚度、阻尼一定时，风电基础的质量越大，机械振动激励对风电基础的影响越小.

（3）风电基础在地震激励作用下的最终响应状态是由所输入的地震激励状态所决定的，即不同震级的地震对结构响应的影响明显不同，地震波的峰值加速度越大，风电基础越容易遭受破坏.

（4）在同样的地震波激励作用下，风电基础的动力响应与黏性阻尼系数的大小无关，而刚度大小的改变对其最终的动力响应有明显影响，在一定范围内，随着刚度的增加，风电基础位移、速度波动越大.