基于Kriging-RSM框架结构整体承载能力抗震可靠度分析*
2021-03-30狄生奎王立宪
狄生奎, 张 宝, 王立宪
(兰州理工大学 a. 甘肃省土木工程防灾减灾重点实验室, b. 西部土木工程防灾减灾教育部工程研究中心, 兰州 730050)
现阶段,结构可靠度的研究主要还停留在构件层次上,由于结构体系可靠度更能真实反映结构可靠性,应对结构体系可靠度进行研究.但结构体系可靠度求解仍存在结构失效模式难以识别和失效模式间相关性难以处理等问题[1-3],对其求解具有较难的操作性.因此,开展关于结构体系可靠度近似计算方法的研究具有重要意义.
结构整体可靠度是应用结构整体极限状态方程近似计算得到的,但结构整体极限状态方程通常是非线性的,甚至是高度隐式的,这就造成了一次二阶矩法等传统显式计算方法不能直接用于计算.由于地震作用的随机性和复杂性以及抗震设计的重要性,结构整体抗震可靠度一直是结构整体可靠度的研究重点,众多专家学者对此开展了大量研究,可以大致将计算结构整体抗震可靠度的研究方法分为两类:1)应用传统响应面法[4]和蒙特卡洛法[5]计算结构整体抗震可靠度;2)应用随机Pushover分析法[6]获取结构整体极限状态方程中隐式因素的前二阶统计信息,再结合矩法、改进的广义一次可靠度方法和改进的高阶矩法对钢筋混凝土框架结构整体抗震可靠度进行计算分析[7].上述计算方法均将有限元分析与可靠度理论有效地结合在一起,深入系统研究结构抗震整体可靠度,并获得大量实用的研究成果,但同时存在计算过程过于复杂、效率不高等问题.本文将Kriging与RSM结合提出一种计算简单、效率高的计算结构整体抗震可靠度新方法.
本文应用Kriging-RSM算法对结构整体承载能力极限状态下的钢筋混凝土框架结构整体抗震可靠度进行计算分析.根据所选取的样本点,建立钢筋混凝土框架结构有限元模型,进行非线性推覆分析选取结构基底剪力,应用Kriging-RSM算法计算承载能力极限状态下的钢筋混凝土框架结构整体可靠度.
1 结构整体承载能力极限状态方程
将结构极限基底剪力VS作为结构整体抗震承载能力,并将结构底部的水平地震作用FE作为结构整体地震作用需求,建立结构整体承载能力极限状态方程,即
Z=g(VS,FE)=VS-FE
(1)
式中,VS和FE均为随机变量.
1.1 极限基底剪力
结构极限基底剪力VS与结构构件的极限承载力、材料本构关系、结构各构件的相关性、抗力与荷载间的相关性、荷载路径、结构型式等因素有关.一般将结构极限基底剪力VS用一组影响因素随机向量X=[X1,X2,…,Xn]T来表示,即
VS=h(X)=h(X1,X2,…,Xn)
(2)
对于结构基底剪力的数值模拟存在以下问题:1)高度非线性.结构极限基底剪力VS与众多不确定因素有关,尤其在结构进入非线性破坏阶段,VS将会更加复杂,非线性程度更高.2)隐式函数.由于结构极限基底剪力VS高度复杂性导致其多半是一个隐式函数.
1.2 地震作用概率模型与统计分析
地震作用FE可利用单自由度振动反应谱表示为等效静力随机模型[8],其表达式为
(3)
式中:G为结构的等效总重力荷载;D为附加随机因子;α为地震影响系数;Am为最大地面加速度;g为重力加速度;β(T,ξ)为动力放大系数.
文献[8]表明,确定烈度的随机地震作用FE服从极值I型分布,其表达式为
FE=(f|I=J)=exp{-exp[-ν(f-u)]}
(4)
式中:f为概率密度函数;J为烈度;ν和u为分布参数,其表达式为
(5)
其中,μJ和δJ分别为第J烈度随机地震作用的平均值和变异系数.
2 Kriging-RSM算法建立
2.1 Kriging模型
Kriging模型是由回归计算模型和非参数模型随机过程联合组成.相比于其他模拟工具,Kriging模型是一种更具有“统计性”的数值模型,比单个参数化模型具有更强的预测能力与精度,这使得Kriging模型所模拟结果的有效性不依赖于随机误差的存在,即已知信息中是否包含噪声信息不会影响Kriging模拟结果的有效性程度.随机过程z(x)的协方差数学表达式为
E[z(x)z(w)]=σ2R(θ,ω,x)
(6)
式中:σ2为过程方差;R(θ,ω,x)为样本点ω与x之间的空间相关函数;θ为高斯相关函数的关键参数.通过优化θ能够调节样本点之间的相关性,对Kriging数值模型的模拟精度有着至关重要的作用.
利用己知样本响应值Y的线性组合模拟任意给定样本的响应值,为了保证拟合的无偏性,即真实值与模拟值差值的均值必须为零.因此,依据拉格朗日方程并由最小二乘法可以得出Kriging模型多项式参数与方差的似然最大估计表达式,进而得到Kriging预测模型,即
(7)
式中:r(x)为样本点之间空间相关函数;β*为多项式参数;γ*可以通过方程Rγ*=Y-Fβ*求取,F为样本点设计函数,R为样本点之间空间相关函数.
由于Kriging模型多项式参数β*和方差估计值σ2均与相关函数R(θ,ω,x)中的参数θ有关,因此,参数θ对Kriging模型的模拟有着重要影响.为了寻找θ的最优解可以通过似然最大估计法,使对数似然函数取得最大问题转化为最小优化问题,即
(8)
本文采用的优化算法是DACE(design and analysis of computer experiments)工具中自带的优化算法(模式搜索法),所选用的相关函数为高斯函数.
2.2 响应面法
RSM主要用于解决未知极限状态函数的可靠度求解问题,其原理是利用多项式函数模拟真实未知的极限状态函数,将对未知极限状态函数求解转化为对显式多项式极限状态函数求解.采用不含交叉项的二次多项式表示目标极限状态函数,即
(9)
式中:x1,x2,…,xn为输入值;a,b1,b2,…,bn,c1,c2,…,cn为待定系数,总共为2n+1个参数.采用式(9)模拟目标极限状态函数时,工作量小,且具有收敛快、稳定性好和精度高的优点.
RSM在可靠度问题求解中,一般采用式(10)对样本点进行取值,即
xi=μxi±λσxi
(10)
式中:xi为设计样本点;μxi和σxi分别为随机变量xi的均值与方差.参数λ的取值将直接影响RSM的收敛性、计算精度和效率.若λ取值过大则使得样本点的取值范围过大,失效点有较高概率落于计算取值范围之内,但RSM模拟效果将会较差;若取值过小则使得样本点的取值范围过小,失效点不在计算取值范围之内的概率较大.
本文应用RSM计算可靠度时,为了保证其具有较高的精确度,将验算点重新作为样本点进行多次迭代计算.因此,选取参数λ的值为2,这样既可以保证失效点具有较高的概率落在样本点的取值范围之内,又保证了RSM具有良好的模拟效果.
2.3 Kriging-RSM算法
Kriging模型虽然可以精确有效地模拟隐式函数,但Kriging模型并不能提供所模拟函数的显式表达式.因此,Kriging模型往往不能直接用于工程结构可靠度的求解,很难利用一次二阶矩法等需要显式方程的可靠度计算方法求解结构可靠度.本文利用Kriging模型模拟结构极限状态方程,为RSM提供足够的样本点,再通过RSM求解Kriging模型所模拟的结构极限方程的可靠度.
利用Kriging模型预测结构的极限基底剪力VS,其表达式为
VS=predictor(xi)
(11)
式中:xi=[fc0,Ec,fy,E]T,fc0为混凝土轴心受压峰值强度,Ec为混凝土弹性模量,fy为钢筋的屈服强度,E为钢筋的弹性模量;predictor为Kriging模型DACE工具箱提供的预测函数.
将结构极限基底剪力VS模拟结果代入结构整体承载能力极限状态方程,可得
Z=g(VS,FE)=predictor(xi)-FE
(12)
将式(12)编写至RSM算法中,应用RSM计算结构可靠度.
2.4 基于结构静力抗震可靠度计算
利用Kriging-RSM与RSM结合有限元分析方法,计算结构静力抗震可靠度,具体流程如图1所示.
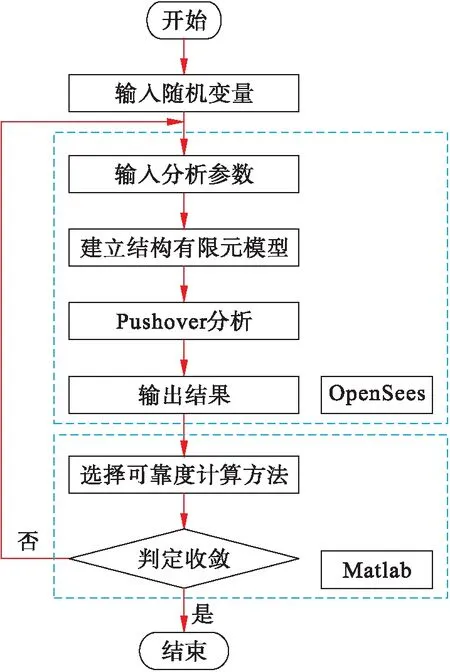
图1 算法流程
将xi=[fc0,Ec,fy,E]T的均值作为第一次计算的设计验算点,利用中心复合设计方法产生样本点,将设计样本点输入至有限元模型中进行Pushover分析.根据分析结果选取基底剪力,利用Kriging-RSM与RSM分别计算结构静力抗震可靠度.若计算结果不收敛,将计算得出的验算点作为下次计算的设计验算点,并重新计算,直至计算结果收敛为止.其中,计算过程的收敛准则为
Δ=(Betai-1-Betai)/Betai
(13)
式中,Betai为第i次计算的结构可靠度指标值.
3 算例与可靠度指标分析
3.1 算 例
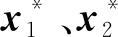

表1 各可靠度计算方法计算结果
为进一步探究Kriging-RSM算法的可行性,应用Matlab软件绘制Kriging-RSM所拟合的极限状态方程曲面,RSM所拟合的极限状态方程曲面以及真实极限状态方程曲面,结果如图2所示.
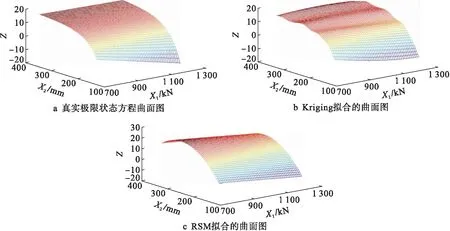
图2 极限状态方程拟合曲面图
由图2可知,相对于RSM所拟合的极限状态方程曲面,Kriging-RSM的拟合结果在整体上更接近真实的极限状态方程,表明Kriging-RSM较RSM具有更好的拟合精度.但在局部上,Kriging-RSM拟合的曲面有微小的褶皱和不平滑,其范围大致在X2取值大于200 mm处.这是因为随着迭代计算次数的增加,新增的样本点取值主要在165 mm附近,造成X2取值大于200 mm的区间缺少样本点,模拟效果较差.
3.2 结构建模与分析
针对一栋三层三跨的钢筋混凝土框架结构,选取其中同一轴线对应的一榀平面框架进行建模分析.结构的立面及梁柱截面配筋图如图3所示(单位:mm).具体设计信息包括:基本雪压为0.3 kN/m2,标准层活荷载为2.0 kN/m2,标准层恒荷载为4.5 kN/m2,屋顶活荷载为0.5 kN/m2.抗震设防烈度为8度,设计基本地震加速度为0.2g,场地土为Ⅱ类.应用OpenSees软件建立有限元模型,混凝土采用Concrete01材料,钢筋采用Steel02材料,采用柔度法纤维梁柱单元.对模型进行震型分析,检查模型的正确性后对结构进行Pushover分析.
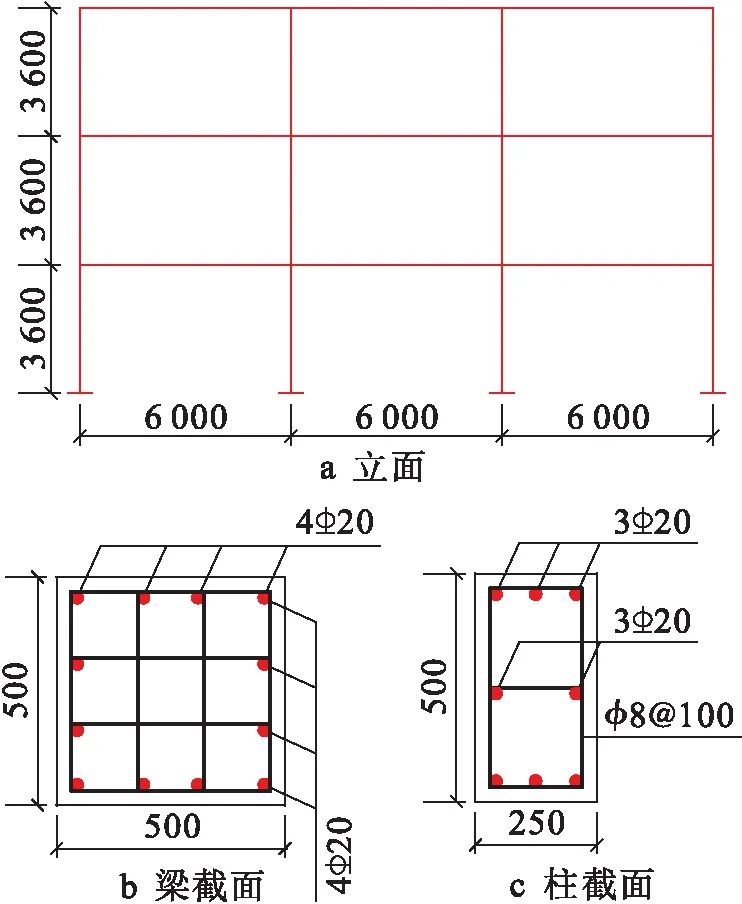
图3 框架立面及梁柱配筋图
建立有限元模型所需要的相关材料随机变量统计参数[9]如表2所示.
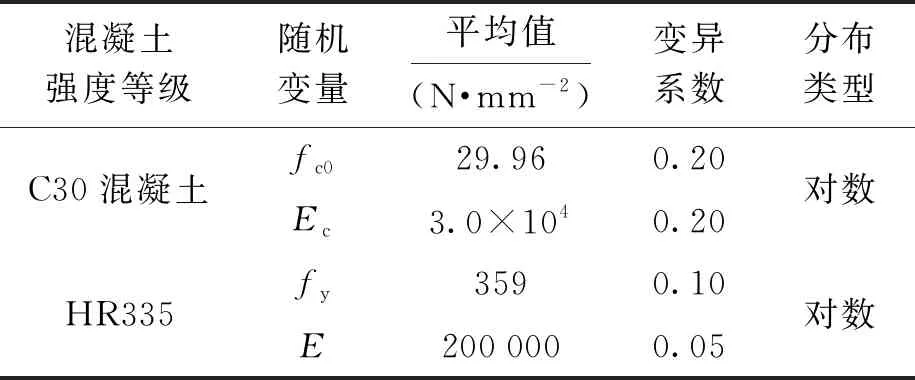
表2 材料随机变量统计参数
表3为不同水平地震FE随机变量的统计参数.为了考虑不同水平地震FE对结构整体可靠性的影响,设计基本地震加速度依据规范取值为0.1g、0.15g、0.2g、0.3g、0.4g,变异系数取为0.3.
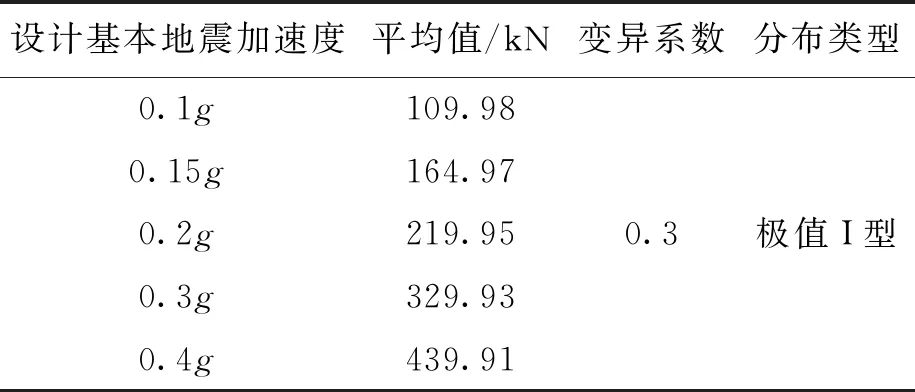
表3 不同水平地震FE随机变量的统计参数
3.3 基于Kriging-RSM与RSM算法可靠度及灵敏度分析
根据上述随机变量参数信息,应用中心复合设计方法产生样本点,建立OpenSees有限元模型进行Pushover分析.可靠度指标的计算结果如表4所示,各随机变量的验算点和灵敏度的计算结果分别如图4~5所示.
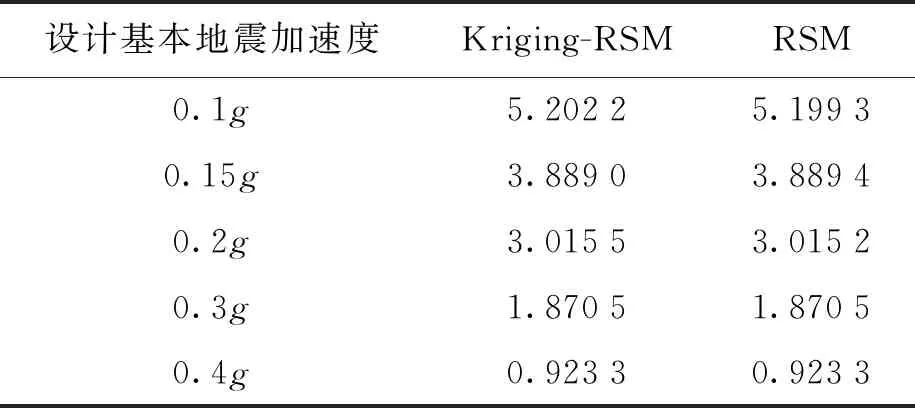
表4 基于Kriging-RSM和RSM的可靠度指标
由表4可知,结构整体可靠度指标随着水平地震作用的增大逐渐下降,并且下降趋势逐渐减缓,且Kriging-RSM与RSM计算得出结构整体抗震可靠度指标较为接近,两种算法最大差值仅为0.002 9.表明结构失效概率随着水平地震作用的增加而增加,进一步验证Kriging-RSM算法对隐式极限状态方程下结构整体抗震可靠度指标求解的可行性.
由图4可知,混凝土轴心受压峰值强度、混凝土弹性模量、钢筋屈服强度、钢筋弹性模量的验算点随着设计基本地震加速度的增加而增加,且逐渐逼近于其各自的均值.其中,钢筋屈服强度增加幅度最大,其次是混凝土轴心受压峰值强度.而地震作用的验算点随着设计基本地震加速度的增加而减小,也是逐渐逼近于其均值.总体来说,在全部随机变量中地震作用的验算点变化幅度最大,其次是钢筋屈服强度.说明随着设计基本地震加速度的增加,各材料随机变量验算点逐渐增大以抵抗地震作用,而地震作用的验算点超出其均值的量是逐渐减小的.
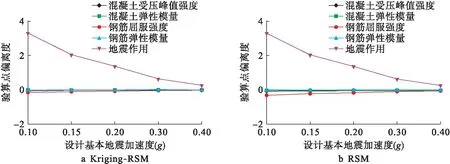
图4 基于Kriging-RSM和RSM结构验算点

图5 各水平地震作用下结构各随机变量灵敏度
由图5可知,Kriging-RSM与RSM计算得出各随机变量的灵敏度值也十分接近.在各不同设计基本加速度下,地震作用始终是对结构可靠度指标影响最为显著的因素.在结构材料随机变量中,钢筋屈服强度对结构可靠度指标影响最大,其次是混凝土的峰值强度,其他随机变量对结构整体可靠度指标有一定影响,但影响效果较小,可以忽略不计.
随着设计基本地震加速度的改变,各随机变量灵敏度均有一定的变化,但这些变化基本上可以忽略不计.这表明在其他条件一定时,设计基本地震加速度不会引起各随机变量灵敏度的改变.灵敏度正负取值情况表明混凝土轴心受压峰值强度、混凝土弹性模量、钢筋屈服强度、钢筋弹性模量为抗力类型随机变量,地震作用是荷载类型的随机变量.
表5为算例中Kriging-RSM与RSM所需的有限元模拟次数.由表5可知,采用Kriging-RSM进行结构整体可靠度计算相比较RSM减少52.5%的计算次数,有效地减少了有限元模拟次数和计算时间,更适合于实际工程应用.对比表4可知,两种算法计算结构的整体承载力极限状态变量可靠度指标具有良好的一致性.两种算法的主要差别在于:Kriging-RSM算法基于各随机变量,可以较好地反映各随机变量对结构功能函数的影响,不需要重复搜索结构的验算点,具有较好的全局模拟效果,计算简单快捷;而RSM算法具有较好的局部模拟效果,收敛速度良好,且具有较好的精度[10].
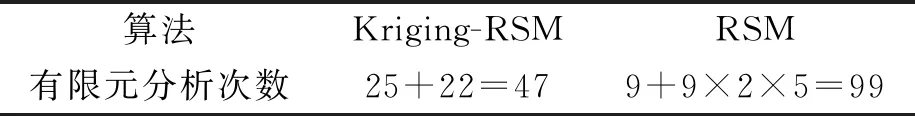
表5 基于Kriging-RSM和RSM算法的有限元模拟次数对比
4 结 论
本文将Kriging-RSM与Pushover有限元分析方法相结合,计算了钢筋混凝土框架整体承载力极限状态下的抗震可靠度与灵敏度,并得出以下结论:
1) 对比蒙特卡洛法、JC法、RSM以及Kriging-RSM关于同一数值算例可靠度指标计算结果,验证了Kriging-RSM能够高效准确地计算隐式极限状态方程下的可靠度指标.
2) 对比钢筋混凝土框架结构整体抗震可靠度的Kriging-RSM与RSM计算结果,发现两种方法的计算结果基本一致,最大差值为0.002 9,进一步验证了Kriging-RSM计算可靠度的可行性,且Kriging-RSM相对于RSM方法,能够减少一半的有限元分析次数,有效地提高了计算效率.
3) 在各随机变量中,地震作用对结构整体可靠度指标的影响最大,其次是钢筋屈服强度;而混凝土轴心受压峰值强度对结构整体可靠度指标具有一定影响,其他因素对结构整体可靠度指标的影响可以忽略不计.设计基本地震加速度能够影响结构整体可靠度指标值,但基本不会改变各随机变量的灵敏度.
