典型环形铸件凝固过程的界面换热系数分析*
2021-03-30邱克强孙治国向青春
邱克强, 张 令, 孙治国, 向青春, 张 伟
(沈阳工业大学 材料科学与工程学院, 沈阳 110870)
铸造模拟软件是模拟铸件充型和凝固的有效工具,并能预测铸件内部缺陷的形成过程、数量和分布位置,为生产高质量铸件缩短了周期和成本[1-2],其精确的温度场模拟十分依赖于材料的热物性能和边界条件,而材料的热物性能比较容易获得.铸件/铸型界面换热系数是边界条件中对模拟精度影响最为明显的参数,且随金属/铸型界面的动态变化而改变,在很大程度上取决于铸型材料、铸件形状和铸造工艺参数.目前获得界面换热系数的方法有热传导数值反算法、界面间隙法、多因素回归法等,其中使用最广泛的是数值反算法,相比于其他方法,该方法以热电偶实测温度为基础来反算界面换热系数,更符合实际传热情况[3-5].
以往对砂型铸造的界面换热系数研究主要针对砂型,而针对铸件/内砂芯界面换热系数的研究甚少.考虑到砂型铸造过程中内砂芯与外砂型传热过程的差异性,本文同时针对砂型和砂芯的界面换热系数进行研究并以实际ZL101合金环形铸件为研究对象,以实验测温为基础,基于Beck非线性估算法[6]建立界面换热系数模型并编制MATLAB反算程序,同时对铸件/外砂型和铸件/内砂芯的界面热流和界面换热系数进行对比研究,并通过比较反算温度与实测温度来验证反算模型的准确性.
1 测温试验方法及过程
1.1 试验材料及尺寸参数
采用ZL101合金环形铸件、呋喃树脂砂造型和制芯,铸件、砂型和砂芯的结构尺寸及测温点位置如图1所示(单位:mm).为保证铸件沿径向传热,砂型上下表面均用石棉绝热,以减小纵向热量传递.图1中1和5号热电偶分别紧贴型腔内表面和砂芯外表面,分别用来测量铸件/砂型和铸件/砂芯的界面温度;2、3和4号热电偶距铸件/砂型界面的距离分别为6、14和22 mm,同样6、7和8号热电偶距铸件/砂芯界面的距离也分别为6、14和22 mm,所有热电偶的高度位置均位于铸件的中间平面上.为防止热电偶相互位置过近导致造型困难,8个热电偶位置并不放置在同一径向上,图1所示热电偶位置为实际热电偶的等效位置.
1.2 测温仪器及试验过程
选择TP_700多功能16通道数据采集仪进行温度数据采集,选取的采集时间步长为0.5 s.考虑到热传导反问题的求解对温度测量高度较为敏感,对热电偶的选择和固定等各方面需要进行综合考虑.热电偶响应时间也会产生较大误差,热电偶接头尺寸需要尽可能小.选择直径为0.3 mm的K型热电偶,热电偶接头采用点焊连接,保证热电偶接头具有更快的响应时间[7].为了减小热电偶位置偏差,热电偶前端由直径为4 mm的双孔陶瓷刚玉管固定,且热电偶与铸件轴线平行放置以减少其对温度场的破坏,从而保证热电偶不会产生明显测量误差.

图1 测温试验装置系统示意图
待测温试验装置准备妥当后,采用ZL101合金用井式电阻炉进行熔炼,完成精炼脱气和除渣后,将合金液浇入测温试验装置中.待铸件凝固冷却完毕后,从数据采集仪上获得所需温度数据.
2 数学模型
2.1 一维温度场
为克服三维热传导反问题计算量大的问题,将铸件/铸型界面换热系数的求解过程简化为一维问题进行处理[8].当求解砂型和砂芯的温度场时,砂型与砂芯的一维瞬态热传导表达式为
(1)
式中:ρ、CP、λ分别为材料密度、等效比热容和导热系数;T为温度;t为时间;x为沿x轴方向位移.等效比热容综合考虑了铸件结晶潜热的释放.
利用隐式有限差分法对式(1)进行离散.一维温度场的简化离散几何模型如图2所示.图2中红色节点为离散单元中热电偶所在位置,各热电偶测试的温度用Tcn(n=1~8)表示,并将Tc4和Tc8作为反算过程的边界温度.
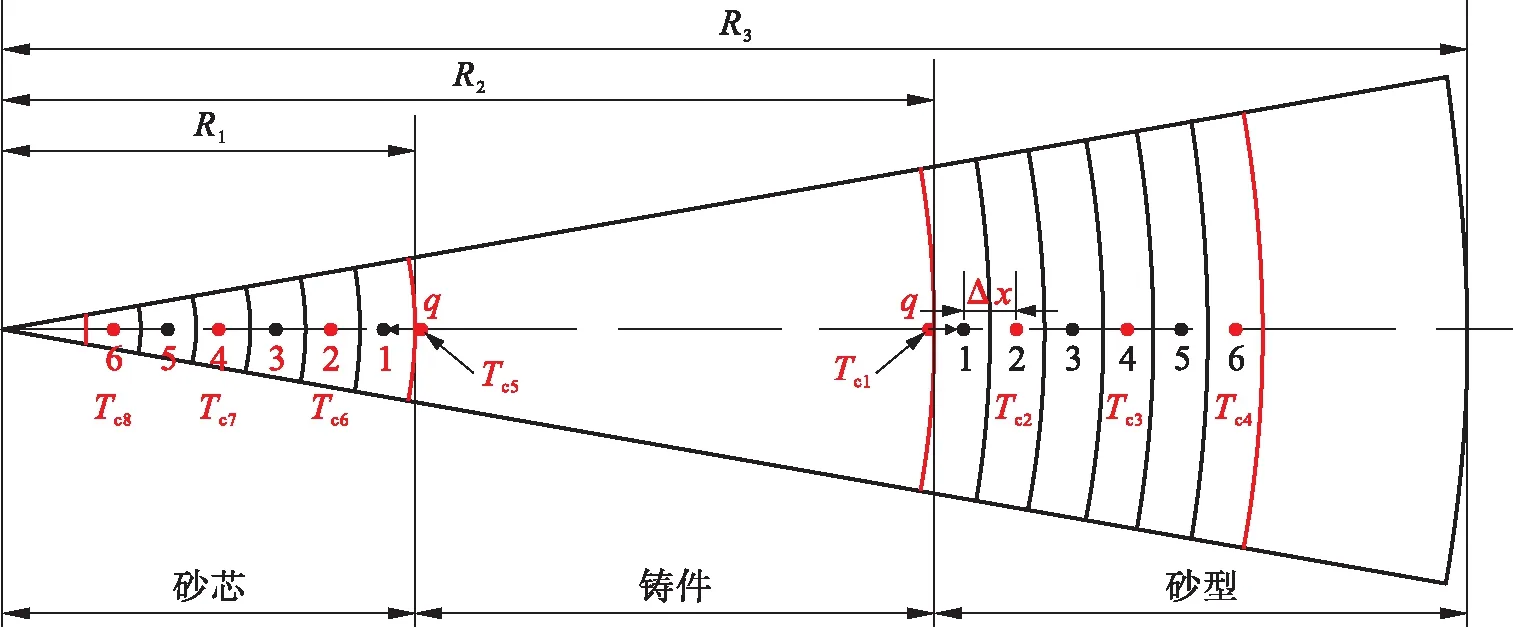
图2 一维温度场的简化离散模型
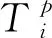
根据能量守恒定律并结合隐式差分格式,得出tp至tp+1时间内各几何单元的温度场数学模型.第1号界面单元温度简化计算公式为
(2)
第2~5号内部单元(i=2~5)温度简化计算公式为
(3)
Sin(i)、Sout(i)和Sq可以分别表示为
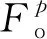
(4)
第6号单元可看作边界单元,其温度与4号热电偶的实测温度相等,即
(5)
每个单元中热流流入面和流出面所对应的半径rin和rout值不同,为了简化数学模型,引入对应单元面积和体积的比值作为几何函数.砂型几何函数简化公式为
(6)
砂芯几何函数简化公式为
(7)
式中,R1和R2分别为环形铸件的内圆半径和外圆半径.
在铸件/外砂型界面处的热流值已确定的情况下,可利用由式(2)~(6)形成的矩阵方程组,通过追赶法对矩阵求逆计算砂型的瞬态温度场.同理,铸件/内砂芯温度场数理模型的建立方法与环件外砂型方法相同,只是由于单元的建立顺序是从铸件/砂芯界面位置为起始单元依次排列,因而其几何函数需更换成式(7).
为使反算结果更精确,材料的热物性参数需要考虑温度变化.树脂砂的热物性参数可从ProCAST软件中的Material Database数据库中获得,砂型密度(ρ=1 590 kg/m3)保持不变,对未知温度下的热物性参数运用多段线性插值法获得导热系数λ和等效比热容CP,其随温度的变化分别如表1、2所示.

表1 树脂砂的导热系数

表2 树脂砂的比热容
2.2 Beck反算模型
求解界面换热系数时,需要结合Beck提出的非线性估算方法确定热流值.本文以求解铸件/砂型的界面换热系数为例进行说明,求解界面热流和界面换热系数的流程如图3所示.当采用非线性估算法求解p时刻的热流qp时,为了减少测量温度所造成的误差,假设p时刻与其未来f个时间步长的热流值相等,且都等于热流初始值q0,从而对热流进行分段处理,即
qp=qp+1…=qp+f-1=q0
(8)
利用[tp,tp+f]时间段内2号和3号热电偶的测量温度Tcn(n=2、3)与计算温度Tmn(q)建立最小二乘法目标函数,其表达式为
(9)

(10)
(11)
(12)
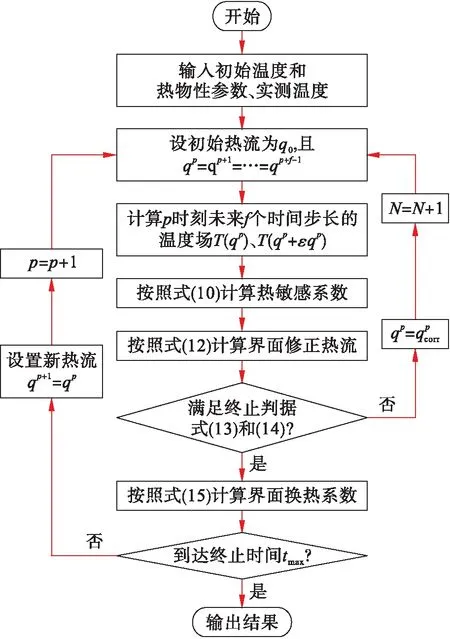
图3 IHTC估算的求解过程流程图
采用式(12)进行迭代获得界面修正热流,每次迭代均需对砂型内部温度场进行计算,直到满足终止条件,其表达式为
(13)
N≤Nmax
(14)
式中:N为迭代次数;Nmax为最大迭代次数.
界面换热系数求解公式为
(15)
利用MATLAB软件编写了反算程序,完成对[tp,tp+1]时间段的界面换热系数求解后,转入下一时间段进行反算,直到计算结束.
3 试验结果及讨论
3.1 测温试验数据分析
图4为典型ZL101合金环形铸件测温试验中热电偶测试温度随时间的变化曲线,其中合金的浇注温度为680 ℃,砂型和砂芯的初始温度均为25 ℃,热电偶Tc1、Tc5的测试曲线分别表征铸件/外砂型和铸件/内砂芯的界面温度.由图4可见,约120 s后金属液的过热温度被消除,冷却曲线斜率明显变化,这表明合金开始凝固,约850 s后合金达到共晶成分进行共晶凝固,约1 750 s后凝固过程结束,铸件冷却速率增加.观察图4可以发现,内砂芯和外砂型的温度场变化相差很大,整个过程中外砂型温度均低于铸件温度,而内砂芯温度约在2 500 s后逐渐高于铸件温度.此外,Tc4、Tc8温度曲线约在100 ℃前产生曲折现象,这可能是由于砂型(芯)内部残留的水分在受热过程中以水蒸汽形式渗透出去,从而吸收一定热量,导致其温度曲线有所偏离[8-9].
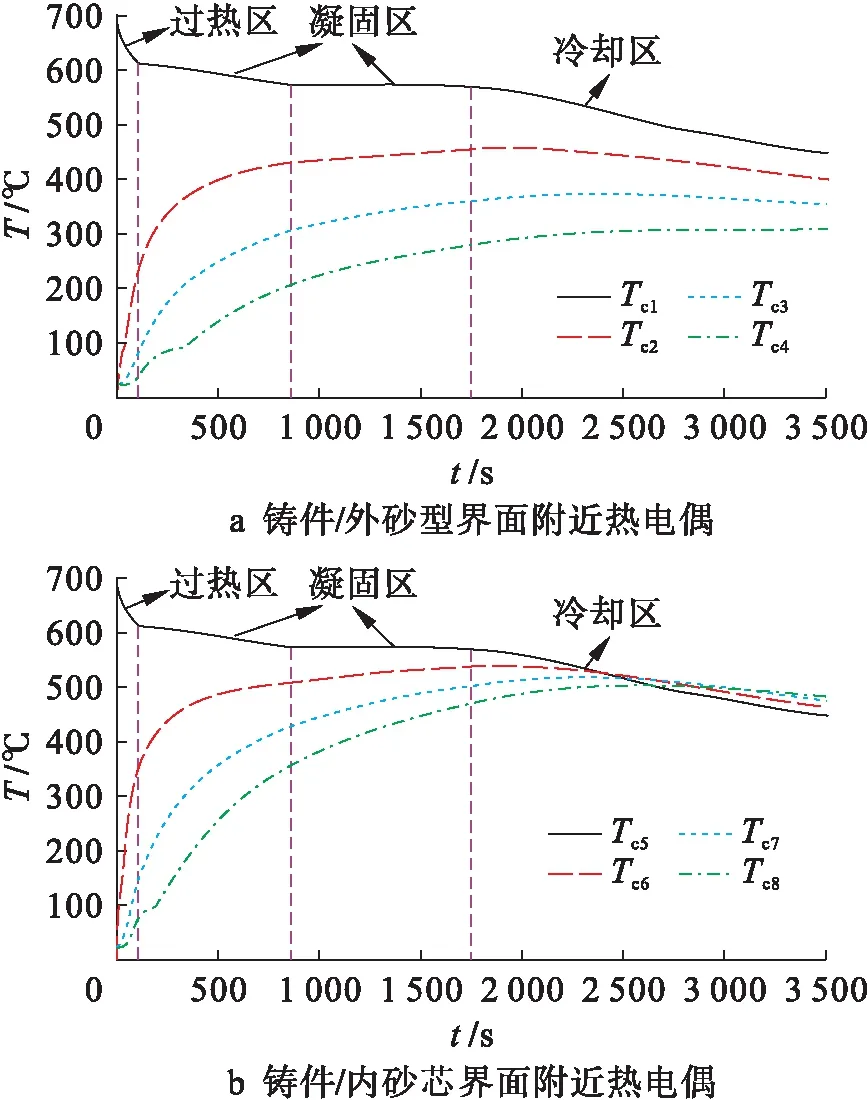
图4 热电偶测试温度随时间的变化
3.2 反算结果及讨论
根据图4所示的实测温度数据,通过反算程序反算出外砂型和内砂芯的瞬态界面热流密度、表面单元温度和界面换热系数.反算过程中未来时间步长的个数f取值为6,此时求解过程更稳定,结果更趋于真实值.
外砂型、内砂芯与铸件界面的瞬态界面热流如图5所示.由图5可见,前80 s外砂型和内砂芯的界面热流分别迅速升高到62、93 kW/m2.凝固开始时界面热流密度应该是最高的,而实际上从热量扩散到热电偶并感应出型(芯)温度的这段时间内,热流被低估了,而型砂的低热传导率特性放大了这一特点,因而出现了初期界面热流上升阶段[10].初期砂芯界面热流要高于砂型,这是由于受到几何函数公式(6)、(7)的影响.随着铸件与型(芯)温差的减小,砂型、砂芯界面热流都会快速下降,砂型界面热流数值趋于稳定在6 kW/m2;而约2 500 s后砂芯界面热流降为零,随后产生反向热流并逐渐趋近于-2 kW/m2,这是后期砂芯内部温度高于铸件温度所引起的,这一结果也符合图4b所示的温度数据.
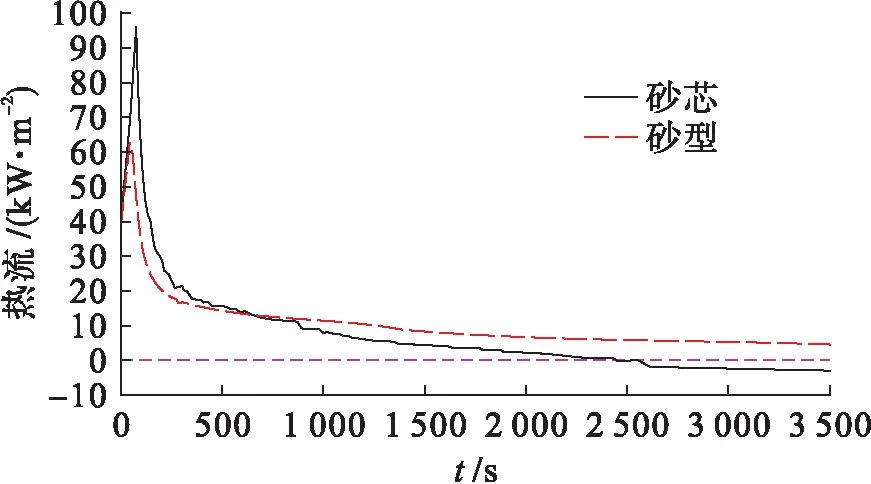
图5 外砂型、内砂芯与铸件界面的瞬态界面热流
砂型和砂芯表面1号单元的温度如图6所示.由图6可见,反算出的外砂型和内砂芯的表面单元温度在120 s之前急剧上升,这阶段金属液处于过热区,铸型和金属液温差很大,产生很大的界面热流使得铸型温度快速上升,且这段时间砂芯表面温度比砂型上升更快,可以归因于初期砂芯的界面热流大于砂型界面热流.经历金属液过热区后,砂型和砂芯两者表面温度变化趋势十分接近,其温度上升速率逐渐降低,约1 750 s后铸件潜热释放完全,砂型和砂芯表面温度达到最高值随后温度平稳下降,且二者温差也逐渐减少,其根本原因是两者热流都在逐渐减少.
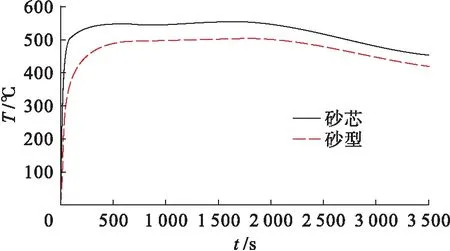
图6 砂型和砂芯表面1号单元的温度
外砂型、内砂芯与铸件界面的瞬态界面换热系数如图7所示.由图7可见,砂型和砂芯的界面换热系数差别很大.整个过程砂芯的界面换热系数都要高于砂型,这是由于内砂芯和外砂型所在位置不同而引起的传热差异所致.0~80 s初期阶段内砂芯和外砂型的界面换热系数分别由145 W/(m2·℃)增加到180 W/(m2·℃)和由83 W/(m2·℃)增加到118 W/(m2·℃),这是由于最初热电偶的响应时间特性问题而产生如图5所示的实际界面热流被低估现象,从而使得初始反算界面换热系数低于真实值,随着反算模型的不断修正迭代,界面换热系数随后上升并趋于真实值.在80~400 s这一阶段,两个界面换热系数都先减少再增加,这主要是受到树脂砂导热系数的影响[11],两个界面换热系数达到最小值时对应的界面温度约为600 ℃,而此时树脂砂的最小热传导系数约为0.5 W/(m·℃).金属液约在120 s后开始凝固,120~400 s期间内的金属液凝固收缩形成的间隙太小,因而不能作为主要影响因素.400 s后砂型和砂芯的界面换热系数变化差别可能是由于铸件收缩引起界面间隙发生动态变化的缘故.当环形铸件发生凝固收缩和冷却收缩时,内砂芯与铸件之间会变得更加紧密,不会产生明显的界面间隙,因而400 s后铸件/内砂芯的界面换热系数未发生太大变化,仅在2 500 s后界面热流方向改变后,铸件/内砂芯的界面换热系数呈现增加趋势.与内砂芯不同,外砂型与铸件的界面间隙在凝固过程中会变大,从而使得间隙内的气体导热对传热热流产生较大影响,而外砂型与铸件界面间隙的变大会使界面换热系数减小[12].结合图4、7可知,针对图4a中合金在400~850 s的凝固收缩后半段和1 750 s后的冷却收缩阶段,图7中相对应的铸件/砂型界面换热系数降低,而在850~1 750 s阶段铸件温度变化不大,相对应的铸件/砂型界面换热系数也基本保持恒定,表明铸件收缩形成界面间隙是影响铸件/砂型界面换热系数的主要因素,且砂型界面换热系数受铸件收缩的影响相比砂芯更为明显.
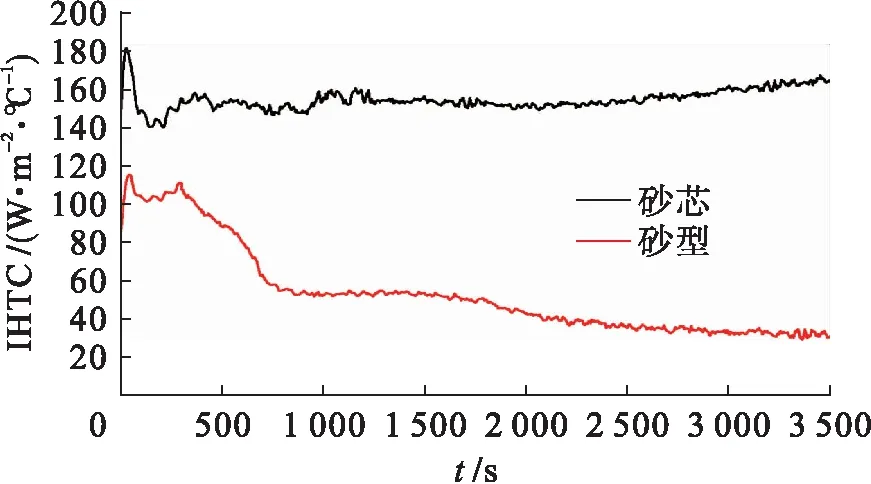
图7 外砂型、内砂芯与铸件界面的瞬态界面换热系数
3.3 界面换热系数反算结果验证
图8为砂型中第2号热电偶与砂芯中第6号热电偶所在位置处的实测温度与计算温度之间的差值.由图8可见,实测温度与计算温度之间的差值在前80 s内均较大,但随着时间的推移,反算程序自身的迭代修正使得计算误差逐渐减少.100 s前Tc2和Tc6热电偶位置处实测温度与计算温度之间的最大绝对差值分别为22、20 ℃,而100 s后该最大绝对差值分别为1.3、0.5 ℃,表明反算过程对计算误差的修正已使反算温度和实测温度十分吻合,因此,采用本文反算方法法求解环形铸件与砂型(芯)的界面换热系数是准确和可靠的.
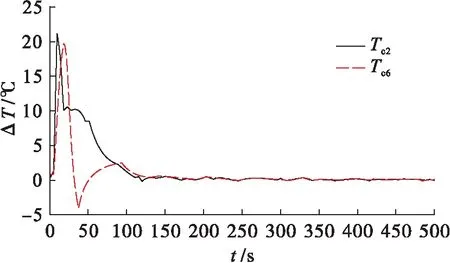
图8 Tc2和Tc6处实测值与反算值之间的温差
4 结 论
本文设计了砂型铸造环形铸件的测温试验方案,建立了界面换热系数的反算数学模型,为砂型铸造铸件凝固传热规律的更精确研究打下了一定基础.以实测温度为依据,利用反算数学模型和反算程序得到了铸件/砂型和铸件/砂芯的界面热流和界面换热系数随时间的变化曲线,为数值模拟软件中界面换热系数这一重要模拟参数的设置提供了参考借鉴.凝固过程中铸件/砂芯的界面换热系数要大于砂型,且铸件/砂型的界面换热系数受铸件收缩的影响相比砂芯要大得多.由反算程序计算出来的反算温度与实测温度基本吻合,表明反算数学模型和反算程序准确可靠,可应用于铸造模拟软件来提高模拟精度.
