基于CAID的工业设计透视草图三维模型重建方法*
2021-03-30徐明亮段景辉
徐明亮, 段景辉
(三亚学院 a. 艺术学院, b. 信息与智能工程学院, 海南 三亚 572000)
在进行工业设计时,设计师往往都会将其自身的创意与设计理念通过绘制产品草图与效果图来实现[1].CAD技术出现后,工业设计可直接通过三维造型实现.然而大部分优秀的设计师更加喜欢通过手绘的方式画出产品效果图[2].传统CAD系统仅可完成建模,无法将创意可视化,导致绘制产品效果图与自身创意不符.计算机图像技术的发展,令计算机识别草图构建三维模型成为可能.
目前,常用的三维模型重建方法主要有基于RHINO的模型重建方法[3]、基于非量测相机图像的设计图模型三维重建方法[4]和自由形态建模方法[5]等,然而上述方法均需对深度坐标进行计算,建模周期长、成本高,实现过程复杂.本文在计算机辅助工业设计(CAID)软件设计的基础上,提出一种工业设计透视草图三维模型重建方法.
1 材料与方法
计算机辅助工业设计技术为工业设计理论和CAD技术的结合,能够和工业设计特点与工业设计师设计思维相适应.CAID系统将工业设计知识当成主体,将计算机当成辅助设计工具[6],充分展现了工业设计理念,完成对设计的定量化描述,借助计算机快速高效的特点,令工业设计效果更加合理化.
基于CAID的工业设计透视草图三维模型重建方法主要包括两个重要阶段,首先需对透视草图进行识别,然后对其进行三维模型重建.
1.1 透视草图识别
通过分步处理的方式对透视草图进行识别,先依据草绘笔划特征对笔划进行分段,然后对其进行识别.
1.1.1 草图笔划分段
笔划分段又被称作关键点检测,关键点就是笔划的分段点,通常是拐点或角点[7-8].关键点检测主要是按照笔划特征,对用户设计意图进行捕捉,把某个笔划分割成若干子段[9].因为只通过某类信息对笔划进行分段会造成分段点数量太多,按照用户草绘习惯,通过草绘过程中笔划的特征对笔划进行分段处理,详细过程如下:
1) 对输入点集合Pj中不同点的坐标进行采集,对角度范围阈值A、速度范围阈值V以及曲率范围C进行初始化处理.
2) 通过下述公式求出与两向量相连的角度值aj,其表达式为
dj=|Pj+1-Pj|
(1)
d′j=|Pj+2-Pj|
(2)
(3)
式中:dj为相连两点间的间隔;d′j为每间隔一点后两点间的间隔.
3) 第j点的速度值vj的计算公式为
(4)
式中:Δdj为两个向量的长度偏差;t为采样所需的平均时间.
4) 相连两个点的近似曲率改变值Δej的计算公式为
(5)
(6)
Δej=ej+1-ej
(7)
式中:ej为第j点的近似曲率值;δj为向量PjPj+1和x轴间的夹角.
5) 如果δj小于A,则认为Pj+1为分段点,将其添加至集合Pout中.如果δj角度在[170°,180°]范围内,且vj低于V,|Δej|≤C,那么Pj为分段点,将其添加至点集中.
6) 把透视草图笔划的第一个点和最后一个点当成分段点添加至点集Pout中.
7) 输出点集Pout.
1.1.2 图形拟合与识别
图形拟合即找到和输入笔迹相近程度最高的图形,笔迹分段则把所有笔迹都分成准直线,所以仅需通过最小二乘法进行直线拟合即可[10-11].
针对透视草图每条笔迹,通过链表形式对其进行保存.可将笔迹R当成是m个像素P(i)的集合,即
R={P(i)=(x(i),y(i))}
(8)
式中,x(i)与y(i)为像素点的坐标.针对各草图笔迹,通过下述过程进行分析:
1) 对笔迹是否是折线进行判断,获取笔迹首尾点P(0)与第m-1个P(i),计算由P(0)与第m-1个P(i)相连的直线方程L.
2) 获取笔迹的长度与宽度,对阈值τ进行计算.
3) 把R中不同点P(i)与直线L间的间隔d(i)和阈值τ相比,如果d(i)<τ,则认为笔迹是直线,通过直线拟合获取端点值.如果d(i)≥τ,则认为笔迹是折线,需对其进行处理.
4) 求出R中不同点P(i)和L间的间隔,获取间隔值最大的点,将其当成角点,把角点保存至角点序列Sii中,从该角点处对笔迹进行分段处理.
5) 对新分段的笔迹继续进行折线判断,直至获取全部角点.
按照顺序对手绘草稿过程中角点序列进行排序,获取新的角点序列Sii,对角点序列中Sii-1、Sii、Sii+1进行处理分析,获取Sii-1与Sii+1连成的直线段L1L2,计算Sii到线段L1L2的垂足O,如果O在线段L1L2中,则继续对其进行处理;反之对下一个角点组进行同样分析.求出Sii与线段L1L2间的间隔d,如果d低于阈值τ,那么Sii为伪角点,将其从角点序列中删除,对下一角点组进行处理[12].
依据新角点序列对保存的草图笔迹数据链表进行分段处理,获取分段后各条直线的链表,完成对其的直线拟合,获取不同端点值,实现对草图的识别.
1.1.3 草图规整
草图规整即把初步识别获取的线元集转变成规则的几何图形,是透视草图三维模型重建的基础与关键[13-14].因为初步识别获取的为零散的线元,未得到最终的空间关系.透视草图规整即判断零散线元可能存在的几何关系,同时引入约束,形成规则的几何图像.
透视草图中含有设计者的设计意图,按照所处环境找到线元可能的空间关系是规整的重要阶段[15].采用依据规则与透视草图上下文的方式完成规整,保证了多图元的规整.依据规则对图元和坐标轴的位置关系进行判断,确定图元间的连接关系.具体方法如下:
1) 依据规则完成判断.如果图元和坐标轴夹角在既定阈值范围内,即可确定位置关系是垂直、平行或特殊角度.
2) 依据草图上下文完成判断.如果两个图元端点间间隔在既定阈值范围内,那么将后一图元端点位置进行改变,实现端点融合.如果椭圆中心和直线间最近间隔与周长之比在既定阈值范围内,表明是相切.如果椭圆中心点间隔在既定阈值范围内,则表明是通信.如果线元间长度之比在既定阈值范围内,则表明是等长.
1.2 透视草图三维模型重建方法
在进行工业产品设计的过程中,特别是对构形进行设计时,一般通过趋近正等轴侧投影图的透视草图形式进行描述.在构形时绘制的线条大部分是消隐的轴测图,如图1a所示,其和通常所见的图形中最接近的可行解用图1b进行描述.所以将封闭的各面片当成三维模型重建的关键,在CAID软件下逐步完成透视草图相应形体的三维重建.
通过图1b所在的坐标系,结合投影的相关知识可知,轴测图可利用异中求同法获取.首先以y轴为核心顺时针旋转θ1角度,然后以x轴为核心逆时针旋转θ2角度,再向xoy平面进行正投影转换处理.获取的轴测映射转换矩阵为

图1 透视草图和可行解
(9)
利用G=[X,Y,Z,1]代表图中各顶点的齐次坐标,在进行轴测转换之后可得到相应顶点的齐次坐标,即g=[x,y,0,1],符合g=GT的映射关系,其中,T为描述转换矩阵.
若轴测图中不同定点映射的二维坐标是确定的,在理论上可利用轴测映射转换的逆转换,即G=gT′,其中,T′为逆转换矩阵,计算顶点三维信息,完成图形的三维重建.然而在实际应用中,分析轴测映射转换矩阵T可知,其没有逆矩阵,无法完成逆转换.
经识别与规整处理后的透视草图空间图形由多个表面构成,将不同面片当成三维重建对象进行分析.利用n=(a1,b1,c1)描述面片的单位法向矢量,则面片上不同顶点的三维坐标平面方程为
a1X+b1Y+c1Z+d1=0
(10)
为了解决轴测映射转换矩阵无法变成逆矩阵的问题,对转换矩阵T进行调整,获取的矩阵为
(11)
经调整后,符合g=GR的映射关系,然而当前矩阵R可逆,则有G=gR′,也就是只要获取面片的法向矢量,以及面片中不同顶点映射的二维坐标值,即可获取相应顶点的三维信息.
在进行透视草图三维模型重建时,可随机针对某面片进行重构,按照该面片和其他面片间的连接关系,对全部面片进行分层分布求解,实现整个透视草图的三维模型重建.
1.3 三维模型重建时面片扩展

(12)
如果q与q″间的间隔过大,或可能出现断层的情况下,仅通过n(q)对n(q′)进行初始化处理,假设γ=α,则有
(13)
利用Δ(a,b)表示q与q″间的关系.首先令a、b低于阈值,提高q与q″的相关性.扩展面片的可见图片集合V(q′)主要包含两部分:1)当前面片的所有可见图片集合V(q);2)最近面片可见图片集合V(q″),把满足角度约束的图片添加至扩展面片的可见图片集合中,则有
V(q′)=V(q)+{n(q′)J(q′)}
(14)
在判断扩展面片中心J(q′)的情况下,通过J(q′)和q所处平面垂直距离获取,J(q′)和面片q所处平面垂直距离计算公式为

(15)
完成对n(q′)、J(q′)和V(q′)的初始化处理后,通过共轭梯度法对扩展面片q′的位置与方向进行调整,收敛后获取面片q′,也就是扩展的新面片,对其进行三维重构,直至扩展至整个图形.面片扩展过程示意图如图2所示.
2 结果与分析
实验在CAID软件下进行,对本文方法进行实验验证.图3为椅子的建模实例.图3a为设计师手绘的透视草图,图3b为经识别处理及规整后图形,图3c为经本文方法得到的三维模型重建结果.透视草图中各特征点的坐标如表1所示.
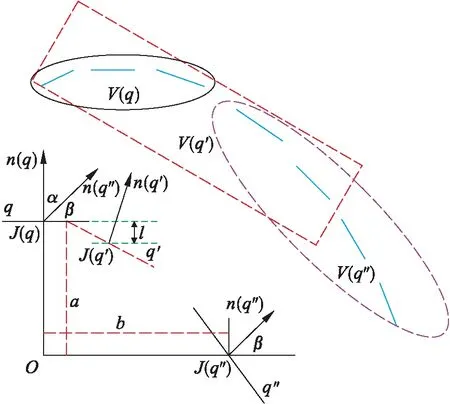
图2 面片扩展过程示意图
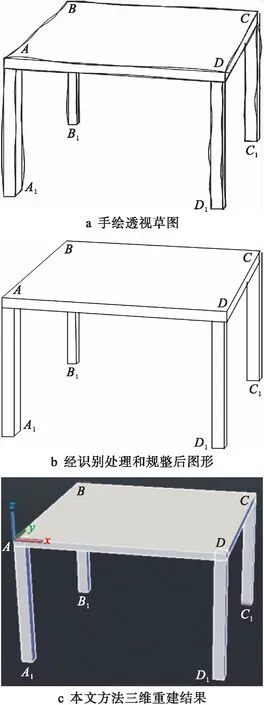
图3 对草图的三维重建实例
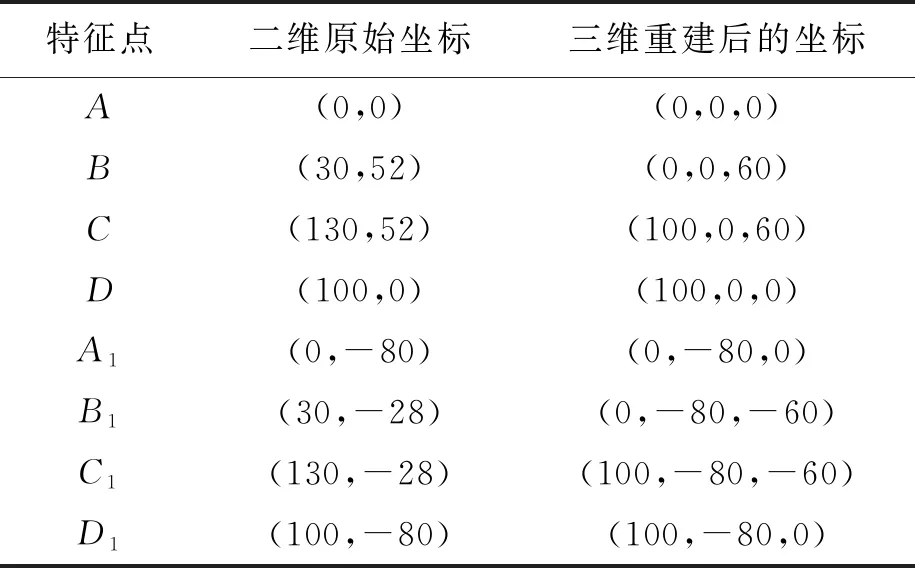
表1 透视草图中各特征点坐标统计
分析图3可以看出,采用本文方法对椅子透视草图进行三维模型重建,得到的重建结果可满足要求,生成了用户所需的模型,是一种有效的三维模型重建方法,可应用于实际的工业设计中.
为了验证本文方法的可行性与精度,设计实验测试模型.在空间直角坐标系中,把研究几何体以y轴为轴心顺时针转角45°,绕x轴逆时针转角40°,在二维面中进行正映射转换,由此得到物体不同顶点的二维坐标值.
根据所提的三维模型重建方法,结合标准差计算法准确获取重建图形不同顶点坐标.对重建结果与原始坐标进行比较,不同坐标间的差异就是计算误差.因为重建过程是通过扩展实现的,所以将顶面作为基础面,将顶面和侧面之间的夹角当作夹角.理论情况下,当前地面和顶面大小相同时,模型变形系数为1,夹角为90°.
为了进一步研究本文方法的重构精度,设计了一组相似性测试算例.将A、B、C、D四个特征点在重建后与平面竖直方向的夹角与理论夹角相对比,以此验证重建精度.在进行测试时,将本文方法作为实验组,将文献[3]中的基于RHINO的重建方法和文献[4]中的基于非量测相机图像的重建方法作为对比组,针对相似算例进行重建,结果如表2所示.

表2 三种方法三维模型重建精度比较
分析表2可知,采用本文方法对透视草图进行三维模型重建,得到的特征点夹角和理论夹角基本一致,说明本文方法重建坐标和理论值最为接近,偏差明显低于文献[3]中的基于RHINO的重建方法和文献[4]中的基于非量测相机图像的重建方法,证明本文三维模型重建方法重构结果和理论值基本吻合,重建精度高,可行性强.
3 结 论
通过分析基于CAID的工业设计透视草图三维模型重建方法,得出如下结论:
1) 按照用户草绘习惯,根据草绘过程中笔划的特征对笔划进行分段处理,找到和输入笔迹相近程度最高的图形,笔迹分段把所有笔迹都分成准直线,采用最小二乘法进行直线拟合,实现图像拟合.把初步识别获取的线元集转变成规则的几何图形,实现草图规整,为透视草图三维模型重建提供依据.
2) 经识别与规整处理后的透视草图空间图形看作由多个表面构成,将不同面当成三维重建的对象进行分析,根据面的法向量以及各个面中不同顶点的坐标值,获得各顶点的三维坐标.在面的扩展过程中,只按照当前面信息对面进行扩展,未综合利用其余面信息,扩展结果连接性较差,同时考虑左右相邻面对扩展面产生的影响,可令三维重建结果更加光滑.
3) 实验结果表明,采用本文方法对椅子透视草图进行三维模型重建,得到的重建结果可满足要求,得到的夹角和理论夹角基本一致,偏差最小,说明所提三维模型重建方法重构结果和理论值基本吻合,重建精度高,可行性强.
