改进万有引力搜索算法在函数优化中的应用*
2021-03-30刘小刚欧阳自根
刘小刚, 欧阳自根
(1. 西京学院 理学院, 西安 710123; 2. 南华大学 数理学院, 湖南 衡阳 421000)
实际工程领域中,许多求解最优类的问题均可以看成是对一个连续函数进行优化,如采矿工程的最优化设计,优化工程控制器的最优参数(PID参数等),工程最优控制问题的数学建模和工程混合料最优配料等.大多数最优求解问题描述如下:
minf(x)
(1)
s.t.mi≤xi≤ni(i=1,2,…,d)
式中:f(x)为目标函数;x=(x1,x2,…,xd)为d维变量;ni和mi为变量的上下限.
由于问题(1)具有复杂性,传统的方法已经不能解决,所以越来越多的研究人员从自然界中生物的群体行为得到启发,将其模型转化为新型的智能算法,并提出许多启发式优化算法,如遗传算法(genetic algorithm,GA),蚁群算法(ant colony optimization,ACO),粒子群算法(particle swarm optimization,PSO)等.这些算法都是针对一些特定问题提出的,目前尚没有任何一种算法能够成功地解决所有的优化问题.因此,继续探索新的启发式智能优化算法是非常有必要的.
万有引力搜索[1](gravitational search algorithm,GSA)最开始是由伊朗克曼大学的教授Esmat Rashedi等于2009年提出的.它是一种依托于物理学中的万有引力定律与牛顿第二定律的新型启发式优化算法.该优化算法通过种群中各个粒子之间的相互作用力(万有引力)来指导群体进行智能优化搜索,与粒子群算法相似.研究[2]证明,GSA算法的优化性能明显优于粒子群和遗传等优化算法.从目前来看,万有引力搜索算法的研究已经在快速发展中.张维平等[3]通过反向学习策略、精英策略以及边界变异策略对GSA优化算法进行改进,有效加快收敛速度和增加物种多样性,继而提高了万有引力搜索算法全局寻优能力;徐遥[4]提出通过引入权值来改变粒子的惯性质量,从而改进万有引力搜索算法,加快了全局搜索的收敛速度;李鹏等[5]提出将改进的GSA算法应用于多目标多约束的微网运行优化问题,最终有效实现了微网优化;李沛等[6]将改进的GSA算法用于无人机的航路规划中,验证了在复杂作战环境下可实时有效规划出无人机的最优航路;龚安等[7]提出引入混沌序列和遗传算法的交叉思想改进GSA算法,有效用于火电厂一次风机的状态监测;李世武等[8]引入自适应配时策略改进GSA,有效解决低排放自适应配时的优化问题.
当然,万有引力搜索算法也有一些缺陷,如GSA存在易陷入早熟和局部最优等问题.因此,本文提出一种新型的改进PSOGSA混合算法.为了验证优化效果,选取四个非线性基准测试函数,并和PSO算法、GSA算法、基本PSOGSA混合算法优化结果进行对比.
1 粒子群万有引力搜索混合算法
1.1 粒子群算法
粒子群优化算法是由Kennedy和Eberhart于1995年提出的一种全局优化进化算法[9],粒子群算法是在对鸟群和鱼群的群体动力学行为研究的基础上演化而来,是对其行为的一种模拟.在群体中,任何一个个体在觅食过程中不仅与过去积累的经验和认知有关,同时还和群体中其他的个体之间存在相互影响.在PSO算法中,每个个体在向最优解过程移动中,都有自己的速度和位置信息,并且这些信息是不断变化调整的(变化的主要依据是粒子过去积累的经验和群体中其他个体的信息).在PSO算法初始化过程中,随机产生粒子群的种群,其中每个粒子都是目标函数的解,为了找寻函数的最优解,每个粒子会根据个体历史最优位置和种群的最优位置来多次调整自己的速度更新策略,然后调整位置更新策略,并经多次迭代寻优最终找到最优解.
每个粒子均有自己的速度向量和位置向量,但在找到最优解之前,粒子会不断更新速度和位置,其表达式为
(2)
(3)
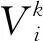
1.2 万有引力搜索算法
万有引力搜索算法是依据万有引力定律、牛顿第二定律及粒子之间受到作用力而相互吸引现象的基础上被提出来的.在万有引力搜索算法中,将优化问题的解看成是一组在空间运行的粒子[10],再根据万有引力定律和牛顿第二运动定律可知,这些搜索粒子由于彼此之间所受到的作用力而向一起聚集.粒子运动遵循动力学规律,惯性质量大的粒子比惯性质量小的粒子运动得慢,因此,物质都朝着惯性质量大的粒子方向进行运动,而惯性质量最大的粒子占据着最优的位置,从而得出问题的最优解.

粒子i的速度、位置更新以及加速度表达式为
(4)
(5)
(6)
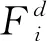
在GSA算法中,为了简化模型,假设引力质量与惯性质量相等,而粒子的惯性质量是依据其适应度的大小计算的,那么粒子的适应度越好,则该粒子的惯性质量越大,吸引力也越大,越接近最优值,但是其移动速度却越慢.根据适应度函数得出的粒子引力质量的更新算法表达式为
(7)
(8)
(9)
式中:fiti(t)为粒子i在t时刻的适应度函数值;worst(t)为粒子i在t时刻群体最差适应度函数值;best(t)为粒子i在t时刻群体最好适应度函数值.第d维空间上粒子i所受到的总作用力为
(10)
(11)
(12)
(13)
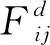
2 改进的粒子群万有引力搜索混合算法
针对GSA优化算法早熟、易陷入局部最优及缺少有效的加速机制等问题,提出了基本PSOGSA混合算法.利用PSOGSA混合算法获取的最优解引导着惯性质量大的粒子朝全局最优移动,但并不是所有粒子都朝着最优解聚集,显然PSOGSA混合算法也加快了群体的整体运动,促使其寻优能力增强,同时也有效缓解了算法停滞的缺点,避免早熟现象.混合算法中将粒子群的速度更新机制引入到GSA算法的速度更新中,有效解决了GSA易陷入局部最优问题.此外,GSA算法在搜索的过程中,更新位置环节只有粒子的当前位置在起作用,而没有群体记忆功能,但是由于引入粒子群算法,可提高粒子间的群体信息共享,基本PSOGSA混合算法速度更新公式为
(14)
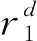
粒子群算法(PSO)是一种新型、原理简单且操作易实现的优化问题解决方法,与万有引力搜索算法同为优化算法.根据无免费午餐定理[11],对于任何一个工程领域中的优化问题,任意两种优化算法的平均性能是相等的,即不存在任何一种优化算法在计算效率、全局搜索能力、通用性等所有算法性能方面都占据着优势.由相关研究[12]可知,粒子群中的gbest加入到速度矢量中会减弱算法的寻优能力,也会进一步平衡混合算法的全局探测与局部开采能力[13-14].因此,本文需要对基本PSOGSA混合算法进行改进,c1和c2的更新公式[15]为
(15)
(16)
式中,h为迭代次数.
为了确保粒子在混合算法后期阶段搜索时具有自适应移动,引入动量因子p来更新粒子位置,即
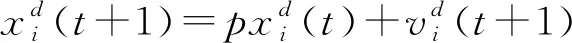
(17)
(18)
(19)
式中:N为种群规模;up为搜索上限;low为搜索下限;ai为粒子i的加速度;pbesti为粒子i的当前最优位置.
为了更加清晰、直观地描述改进的粒子群万有引力搜索混合算法,现给出改进算法的步骤与流程如下:
1) 随机初始化粒子的位置、速度、加速度和质量以及各粒子间所受到的作用力;
2) 设置粒子搜索范围,并计算种群中粒子的适应度函数值;
3) 利用式(12)计算引力常数,式(7)~(9)计算种群每个粒子的质量;
4) 利用式(11)计算种群中两两粒子之间相互受到的万有引力;
5) 利用式(6)计算每个粒子在每个维数上所受到合力产生的加速度,并将其更新;
6) 更新种群中每个粒子的速度和位置;
7) 判断算法迭代次数是否达到最大,或者连续若干次最优值是否一直保持不变,若满足,则停止搜索,否则转向步骤2).
3 仿真分析
3.1 测试函数
为了检验改进的PSOGSA混合算法的优化效果,选取了PSO、GSA和基本PSOGSA算法进行对比实验,并引入四个Benchmark函数进行测试.四个测试函数中,Sphere是一个非线性的、平滑的、对称的单模态函数,变量间可分离,常用来分析算法的执行性能;Rosenbrock是一个非对称的典型病态单模态函数,很难实现全局最优;Ackley和Griewank均为典型的不同维度之间不可分离的、连续的复杂多模态函数,两者均具有广泛的搜索空间,以及大量的局部极小点和高大的障碍物.在这四个函数中,除了Rosenbrock函数在全局最优解[1,1,…,1]处有极小值,其余测试函数均在全局最优解[0,0,…,0]处有极小值,并且极小值均为0.具体函数如表1所示.

表1 测试函数
3.2 实验结果及分析
利用改进的PSOGSA混合算法、PSO算法、GSA算法以及基本PSOGSA算法对上述四个测试函数进行数值实验来验证本文算法的性能.各算法涉及的主要参数设置如下:种群规模N=50;最大迭代次数T=1 000;函数维度d=30;标准粒子群算法中惯性权重w=0.9;加速因子c1=2,c2=2;万有引力算法中引力常数G0=100;PSOGSA混合算法中加速因子c1=0.5,c2=1.5.为了验证改进粒子群万有引力混合算法的优越性和可行性,分别对表1所示的四个函数进行优化,如图1~4所示.
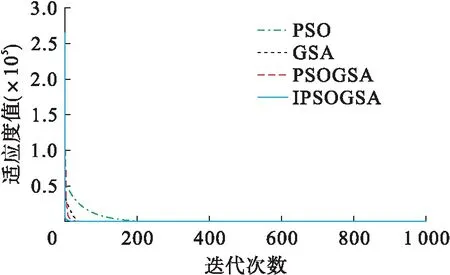
图1 Sphere函数优化曲线
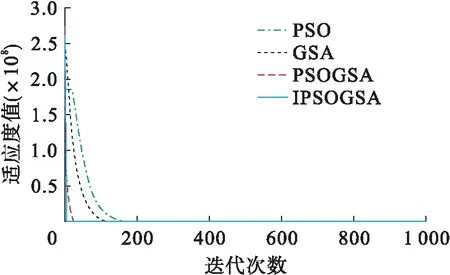
图2 Rosenbrock函数优化曲线
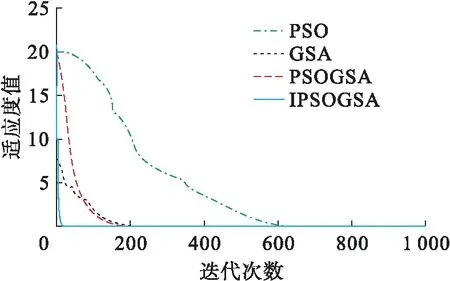
图3 Ackley函数优化曲线
根据图形所示的结果可以看出,改进的粒子群万有引力混合算法在高维函数优化中较其他群智能算法(粒子群算法PSO、万有引力算法GSA和粒子群万有引力混合粒子群算法PSOGSA)相比具有明显的优势,收敛速度快,搜索精度高,避免早熟现象,易找到全局最优解,克服了传统PSO算法和GSA算法中出现的不足和缺点.改进后的混合算法具有更加优良的性能指标,同时也证明改进策略的可行性和正确性.
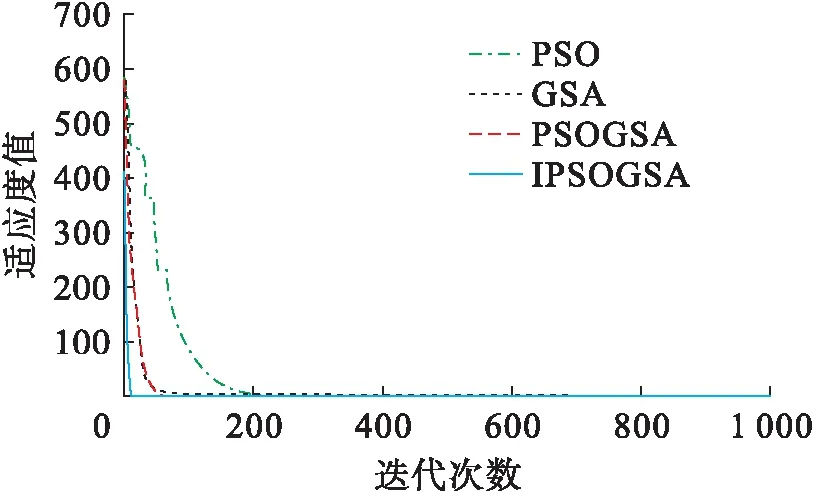
图4 Griewank函数优化曲线
4 结 论
本文在基本PSOGSA混合算法的基础上进行改进,提出了改进的PSOGSA混合算法.由于GSA算法具有早熟、易陷入局部最优及缺少有效的加速机制等问题,将PSO与GSA算法结合,并对c1、c2进行改进,缓解由于gbest加入到速度矢量中而导致算法寻优能力减弱的缺点,同时也平衡了全局与局部最优.为了确保粒子在后期阶段能够自适应移动,引入动量因子p来更新粒子位置.通过四个测试函数对改进的PSOGSA混合算法进行测试,与PSO、GSA和基本PSOGSA混合算法相比,不论是单峰函数还是多峰函数,本文算法均表现出较快的收敛性和较好的稳定性,从而验证了本文算法的有效性.
