Ti-6Al-4V合金超塑性变形行为的人工神经网络预测*

王 鑫， 刘金亮， 周 舸， 刘嘉靖， 李 锋， 张思倩

(沈阳工业大学 a. 材料科学与工程学院， b. 国家大学科技园， 沈阳 110870)

人工神经网络(artificial neutral network，ANN)是一种较为先进且实用的信息处理技术，能够通过输入、输出参数设定、算法选择、运算精度调节等，实现对数据分析过程的自学习、自训练.采用该方法进行数据分析时，既不需要特定的物理模型，也不需要假设与修正，就能够对数据进行自我深度学习，从而获得各参数之间的内在规律，有效解决传统模型构建与数据回归方法中无法解决的难题.因此，针对材料成型工艺参数变化较为复杂且呈现多维度正交变化趋势的研究领域，该方法具有广阔应用前景.为此，国内外学者及相关研究机构进行了如下研究工作：中国科学院金属研究所侯介山等[5]针对NiAl合金的超塑性变形过程，采用BP人工神经网络方法实现了对其在不同成分和不同工艺参数下的断裂伸长率的预测；张学敏等[6]对WSTi3515S阻燃钛合金的超塑性变形行为进行了预测；崔岩等[7]采用人工神经网络技术开展了材料基因工程方面的相关研究工作；刘雅芳等[8]采用RBF型人工神经网络研究了碳/陶瓷复合材料的化学成分对其硬度的影响；张建平等[9]采用人工神经网络算法对6061铝合金稳态应力进行了预测与精度分析；Lakshmi等[10]采用BP人工神经网络技术结合试验验证方法，研究了ASS304合金塑性区域的力学性能变化规律，获得了较好的预测精度；Kapoor等[11]采用人工神经网络技术对Zr-2.5Nb-0.5Cu合金的变形行为进行了系统研究.然而，目前文献报道中关于采用BP人工神经网络技术对Ti-6Al-4V合金超塑性变形行为的研究内容相对较少.

本文以Ti-6Al-4V双相钛合金的超塑性拉伸试验数据为基础构建三层网络模型，并充分考虑模型构建过程中的算法选择与预测精度，分别对该合金超塑性变形过程中的峰值流变应力和稳态流变应力进行预测，从而为该合金的超塑性变形行为提供新的研究方法与思路.

1 材料及方法

试验材料选用厚度为2 mm的Ti-6Al-4V双相钛合金板材，其合金成分如表1所示.

表1 Ti-6Al-4V合金的化学成分(w)

参照GB/T 228.2-2015标准，利用AG 250 KNE型电子拉伸试验机对合金进行超塑性拉伸试验，拉伸试样尺寸如图1所示(单位：mm).试验温度为670～820 ℃，保温时间为10 min，初始应变速率为5×10-3、1×10-3和5×10-4s-1，保护气体为氩气.试样断裂后水淬至室温，从而保留高温变形组织.

图1 超塑拉伸试样尺寸示意图

采用OLYMPUS GX51金相显微镜观察试样超塑性拉伸后的光学显微组织.腐蚀第一阶段(晶界腐蚀)：浸蚀剂为6 mL HNO3+100 mL H2O+3 mL HF；腐蚀第二阶段(区分β相)：浸蚀剂为98 mL C2H2O4·2H2O+1 g Fe(NO3)3+2 mL HF.

2 结果与分析

2.1 BP人工神经网络模型预测的数据基础

金属材料的微观组织，尤其是晶粒尺寸对其超塑性变形性能起着重要影响作用.晶粒尺寸计算方法为

d=1.74L

(1)

式中，L为金相显微组织线截距.

图2为Ti-6Al-4V合金的初始显微组织.结合式(1)和图2，计算得出该合金的晶粒尺寸分别为5.68、6.98和7.95 μm，本文将其分别定义为Ⅰ类(5～6 μm)、Ⅱ类(6～7 μm)和Ⅲ类(7～8 μm).

图2 Ti-6Al-4V合金初始显微组织

选取Ti-6Al-4V合金(Ⅰ类)进行超塑性拉伸试验，获得该合金在不同应变速率下的峰值流变应力和稳态流变应力，结果如图3、4所示.由图3、4可见，随着超塑性变形温度的升高，该合金的峰值流变应力与稳态流变应力均呈现降低趋势.

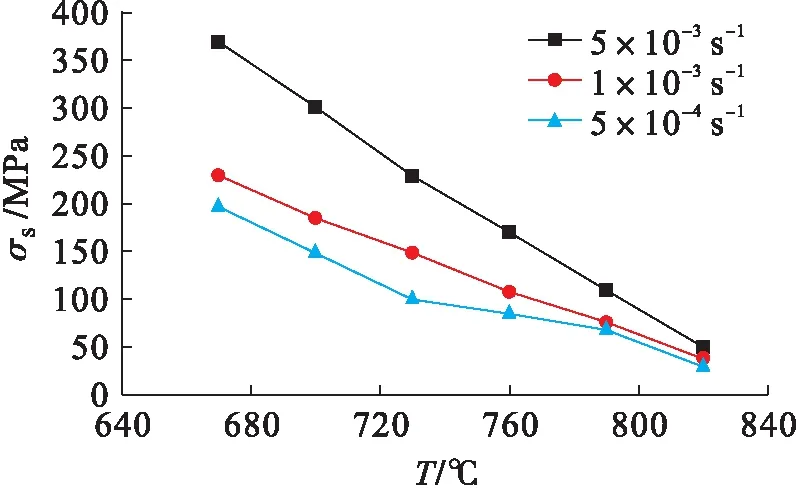
图4 Ti-6Al-4V合金的稳态流变应力变化曲线

选取Ti-6Al-4V合金超塑性变形过程中的温度、应变速率和晶粒尺寸为BP人工神经网络模型的输入参数，而将峰值流变应力和稳态流变应力作为输出参数.在54组数据中随机抽取45组进行神经网络训练，剩余9组数据作为预测样本，具体测试样本数据如表2所示.由表2可见，输入、输出参数数值相差较大，且会产生数值“溢出”现象.

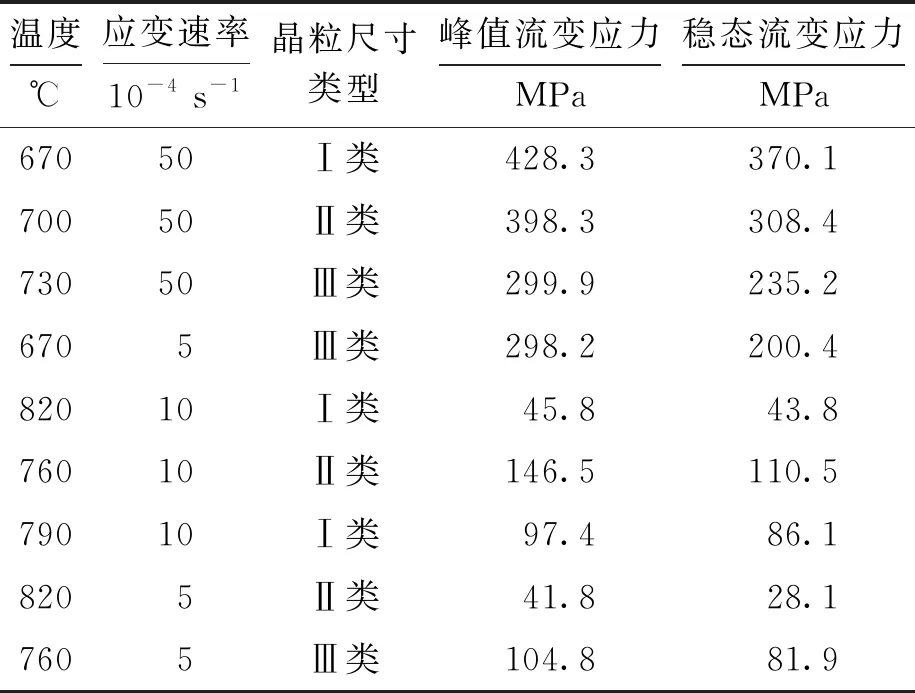
表2 Ti-6Al-4V合金测试样本数据

为了提高预测精度，对训练数据按照式(2)进行归一化处理[12]，即

(2)

式中：Z为原始数据；Zmax、Zmin为原始数据的最大值和最小值；Z′为标准化后的数值.

采用MATLAB自带的BP人工神经网络软件，以试验数据为基础，确定输入、输出参数，利用神经元对输入、输出参数进行反复自学习与训练并对权值和阈值进行调节，直至满足预先设定的精度值后输出结果.本文所构建的BP人工神经网络模型结构如图5所示.当进行BP人工神经网络训练时，温度为670～820 ℃，应变速率为5×10-4～5×10-3s-1，晶粒尺寸为5～8 μm.在三层网络模型中选用Trainlm函数，设定网络预测样本数为45，测试样本数为9，经过3 586次运算后多重相关系数为0.82，网络模型误差范围为2.02×10-4～4.85×10-4，此时得到峰值流变应力为41.8～428.3 MPa，稳态流变应力为28.1～370.1 MPa.

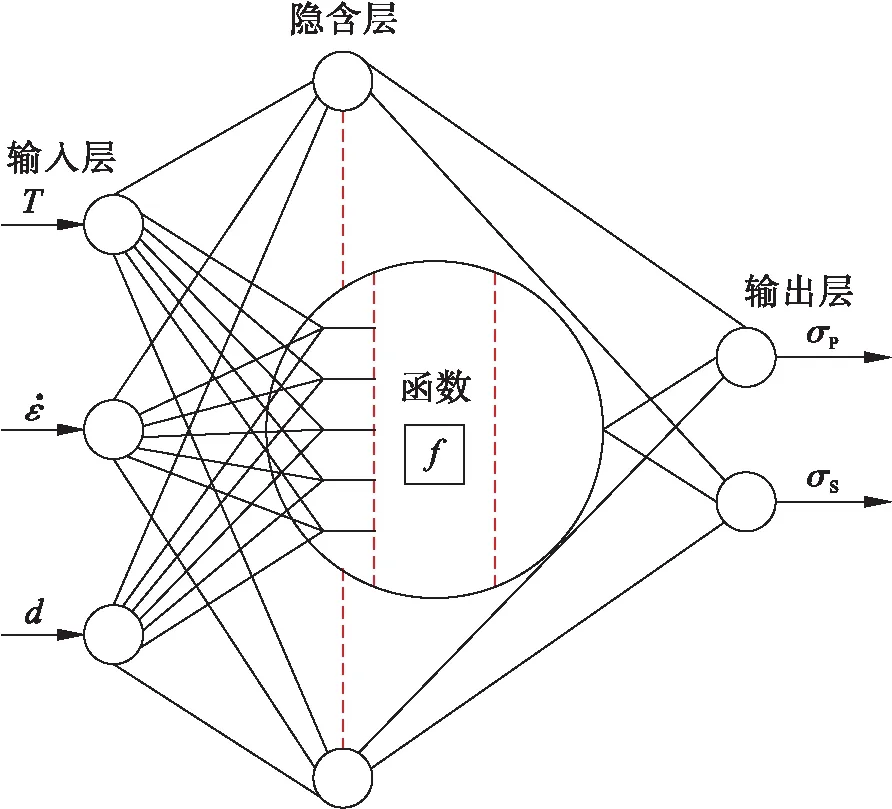
图5 人工神经网络结构和神经元示意图

2.2 BP人工神经网络的训练

图7为分别选用动量LM算法(函数为Trainlm)、MOBP算法(函数为Traindm)、RPROP算法(函数为Trainrp)和SDBP算法(函数为Traingd)4种典型算法预测后的函数收敛曲线.由图7可见，在设定相同预测精度下，当选择LM算法时，最少运算次数函数曲线收敛，表明LM算法的运算效率最高，因此，本文选用该算法进行BP人工神经网络模型的训练与测试.

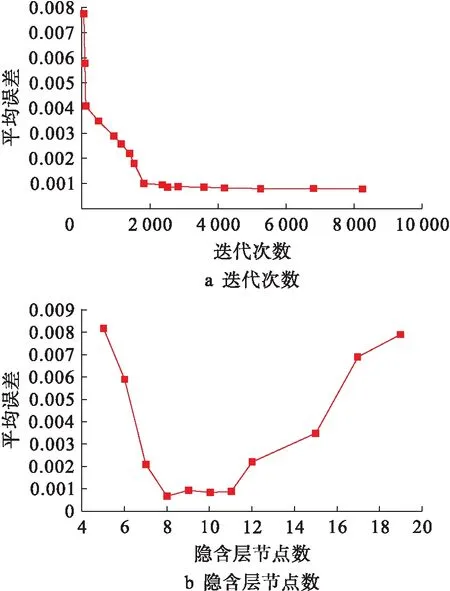
图6 Ti-6Al-4V合金平均误差与迭代次数和隐含层神经元个数的关系

按照温度、应变速率、晶粒尺寸三维交叉均衡选取原则，随机选取BP人工神经网络模型训练后的流变应力值与试验值进行误差分析，结果如表3所示.由表3可见，Ti-6Al-4V合金的峰值流变应力、稳态流变应力的网络预测值与试验数据之间的最大相对误差为5.3%，表明网络预测值与试验值之间吻合度较高，因此，所建立的神经网络模型具有较高的训练精度.

2.3 Ti-6Al-4V合金超塑性流变应力预测

按照表3中的参数构建BP人工神经网络模型，并对Ti-6Al-4V合金超塑性变形过程中的峰值流变应力和稳态流变应力进行预测，结果如图8所示.由图8可见，随着应变速率的增大，峰值流变应力、稳态流变应力均升高；随着变形温度的升高，峰值流变应力和稳态流变应力均降低.当应变速率为5×10-4s-1且温度大于790 ℃时，峰值流变应力和稳态流变应力较低(<60 MPa)，说明当该合金在高温低应变速率下进行超塑性拉伸时，流变应力较低，即合金具有良好的超塑性变形性能.

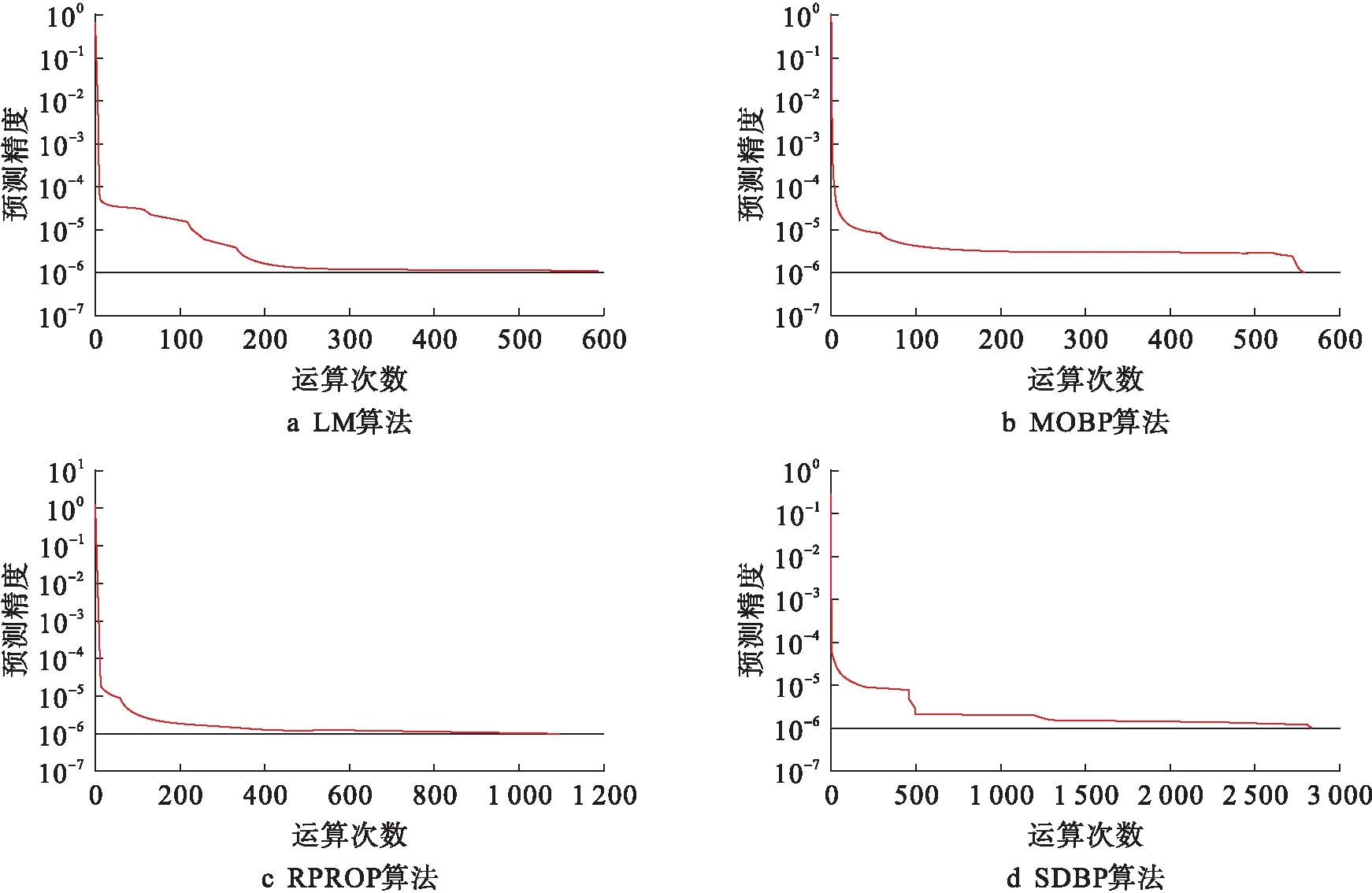
图7 不同训练算法下的函数收敛曲线

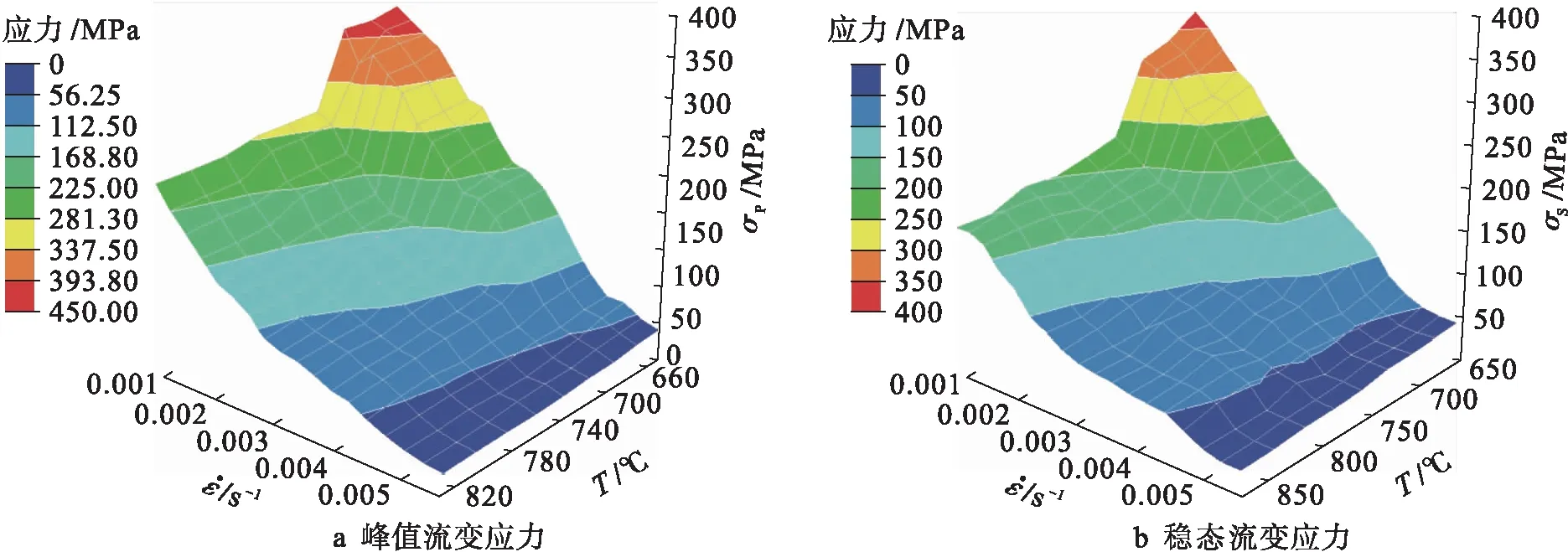
图8 Ti-6Al-4V合金的流变应力变化曲线

3 结 论

采用BP人工神经网络技术建立了三层神经网络模型，对Ti-6Al-4V合金不同超塑性拉伸试验下的峰值流变应力和稳态流变应力进行了较为准确的预测.通过以上分析可以得出如下结论：

1) 当采用LM算法对Ti-6Al-4V合金超塑性变形行为进行BP人工神经网络测试时，运算效率较高且误差分析曲线收敛，具有良好的预测精度，最大误差仅为5.3%.

2) Ti-6Al-4V合金在高温低应变速率下进行超塑性变形时，稳态流变应力和峰值流变应力均低于60 MPa，表明合金具有良好的超塑变形性能.