基于粒子群优化分段聚合近似的负荷分类*
2021-03-30张宇献
张宇献, 董 放
(沈阳工业大学 电气工程学院, 沈阳 110870)
电力需求侧管理是指通过有效的管理措施,提高客户终端利用效率,减少不合理的电力消耗,同时减少客户在电网高峰时段对电力的需求,提高电网运行的经济性[1].但是,实际电力系统中负荷数据十分庞大,不利于负荷数据的管理与调度,所以需要对其进行降维分类处理[2].依据分类得到的典型日负荷曲线,可以合理地利用和分配电力资源,有效缓解电力供需的矛盾.
引起负荷数据产生异常的因素有很多,电力系统的负荷数据由于信道噪声、冲击负荷以及突发事故等因素会存在非平稳特性[3].负荷数据实际上是典型的非平稳时间序列,由时间分辨率决定着其特征维度[4].随着我国智能电网的发展,设备精度的提高使得负荷数据的维度过大,影响分类效果[5],因此,对负荷数据进行降维成为主要研究方向.常见的降维方法有:主成分分析(PCA)、自组织映射(SOM)、符号聚合近似(SAX)及分段聚合近似(PAA)等[6-8].郑旭等[9]通过把小波熵值作为评估子序列复杂度的指标,进而来确定分段迭代次数,可以准确描述原始样本数据.Song等[10]提出了基于分段聚合近似的符号化表示,这种算法的局限性在于特征表示过程中会丢失原始数据中一些比较关键的信息.何勰绯等[11]利用每个时间序列的子序列起点值与终点值作为趋势距离,通过均值和趋势来描述时间序列变化.
本文针对凭经验或经过多次实验确定分段聚合近似算法压缩比这一缺陷,提出一种基于粒子群优化分段聚合近似的方法.利用粒子群算法对压缩比取值进行优化,在降低数据维度的同时考虑对降维后样本的质量与分段数的权衡,最后采用基于相似性的分类方法对负荷数据进行分类,使得分类后的同类负荷数据曲线相似性最大,实现电力负荷有效分类.
1 基于小波变换的平滑处理
连续小波变换(WT)将函数f(t)在该小波基下进行变换,其表达式为
WTf(a,τ)=[f(t),ψa,τ(t)]=
(1)
式中:ψ(t)为小波基函数;a为伸缩量;τ为平移参数.
在小波分解过程中,分解层数的选择对于结果至关重要.分解层数越大,则噪声和信号自身特性越明显,但分解层数越大导致重构信号失真也会越大,在一定程度上影响去噪效果.考虑本文负荷数据采样频率较低,选择较少分解层数.
采用无偏风险估计阈值,并对每个阈值求出其所相对应的风险值,风险最小的设为所选阈值,即
(2)
式中,kmin为风险曲线最小风险点所对应的值.
考虑硬阈值函数在阈值点处并不连续,因此重构出来的信号可能会产生振荡现象,本文选用连续性较好的软阈值函数来进行数据的平滑处理.软阈值函数为
(3)
式中:Wj,k为小波系数;Thr为由阈值确定准则得出的阈值估计值.
2 基于APSO分段聚合近似算法
2.1 分段聚合近似基本原理
对于一个长度为m的数据S=(s1,s2,…,sm),用一个长度为w的数据S′=(s′1,s′2,…,s′w)对其表示,其中,w≤m且w能被m整除,则该方法是一个压缩比为Nk=m/w的时间序列数据降维过程.
通过将长度为m的数据s转变为长度为w的数据s′,并且用该段所包含数据元素的均值来近似表示该序列段,该过程称为分段聚合近似.在实际研究过程中发现,利用PAA算法进行数据降维时,选取不同的压缩比会导致数据的分段数目不同,最后得到的结果也不相同,因此对每个负荷数据选择合适的压缩比是利用PAA算法进行数据降维的关键.
2.2 基于APSO的压缩比设定
当采用PAA方法进行负荷数据降维时,需要对PAA算法压缩比的取值进行合理的权衡.本文采用加速粒子群算法(APSO)对PAA压缩比进行优化,以提高全局搜索能力.
在APSO中,粒子的速度和位置更新表达式为
(4)
(5)
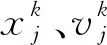
APSO-PAA算法描述如下:
1) 求出当前负荷数据S的压缩比Nk;
2) 对负荷数据S进行分段表示,得到不同压缩比下的PAA序列;
3) 初始化粒子群,将近似表示的负荷数据与原始负荷数据之间的欧式距离设置为粒子群算法的适应度函数;
4) 重复步骤1)~3),直到近似表示的负荷数据与原始负荷数据间的欧式距离最小,并输出当前位置的压缩比;
5) 通过第4步计算的压缩比得到该负荷数据最佳分段数,用PAA方法将长度为m的负荷数据表示为w个区间.
3 负荷分类
本文采用模糊聚类对负荷进行分类.模糊聚类通过优化目标函数得到每个样本点对所有类中心的隶属度,达到对样本数据进行划分的目的.对于给定的负荷时间序列样本S={s1,s2,…,sm},将其进行划分为c个类,聚类中心分别为v1,v2,…,vc,则其目标函数为
(6)
式中:n为数据集中的样本数:c为样本聚类中心数;sj为第j个数据样本;ei为第i个聚类中心;ui,j为第j个样本属于第i个类的隶属度;M∈[1,∞)为权重因子,一般M的取值为1.5≤M≤2.5.
聚类有效性函数是用来衡量聚类结果与聚类数目的依据,本文采用改进划分系数的聚类有效性函数,该指标函数结合了类群之间的差异性和类内各样本之间的相似性,有效性函数越大,说明分类后类内样本之间的相似性越大,不同类簇之间差异度越大,代表聚类效果越好.
4 算例验证
为验证本文方法有效性,选取国网辽宁省网公司在相同时间段内不同行业的58个典型日负荷数据集,时间间隔为15 min,每个典型日负荷曲线数据有96个数据点.为了消除数量级差异对聚类结果的影响,在进行聚类分析之前先对其进行归一化处理,得到典型日负荷曲线数据集.
4.1 小波分解平滑处理
本文采取db3小波基、分解层数为5、软阈值的方法对典型日负荷曲线集进行降噪处理,获取去噪后的负荷数据.从数据集中选取负荷曲线26为其中一个负荷曲线,小波阈值去噪后结果如图1所示.
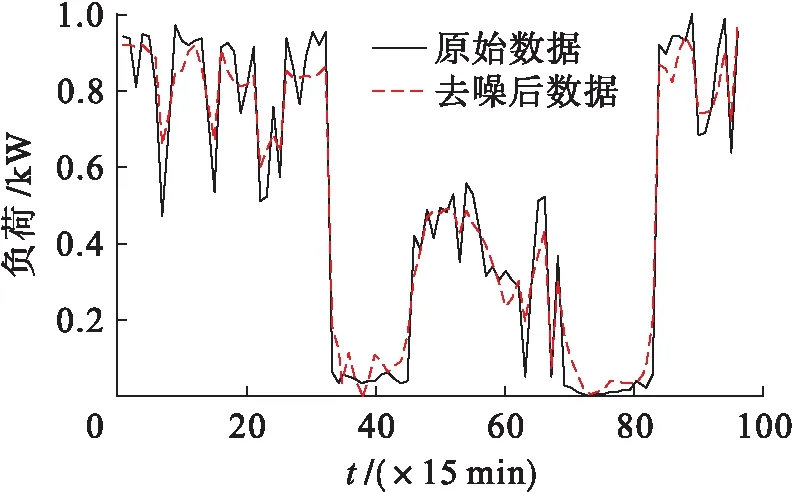
图1 小波阈值去噪结果
4.2 分段聚合近似
选取负荷数据样本5、23说明压缩比设定的重要性.数据样本5在不同压缩比下的分段聚合近似结果如图2所示.从图2可知,在压缩比Nk=12时,5号样本接近原负荷曲线,此时拟合误差为1.322 3;Nk=6时曲线拟合误差为1.972 8,该负荷曲线在压缩比Nk=6时的拟合误差大于Nk=12时的拟合误差.

图2 数据样本5在不同压缩比下的分段聚合近似结果
数据样本23在不同压缩比下的分段聚合近似结果如图3所示.在Nk=12时,负荷曲线23刚开始出现波动,分段近似表示后曲线拟合效果较差,此时误差为2.016 7;而曲线在Nk=6时误差为1.158 0,近似表示效果更好.
将负荷数据进行APSO-PAA变换,根据误差确定压缩比,对58个负荷数据集进行APSO-PAA变换得到的压缩比如表1所示.由表1可以看出,经过APSO-PAA变换后的负荷数据的选取压缩比各不相同,对于形态特征相对复杂的负荷曲线可以分配更多的分段数,以确保近似表示后数据的精度.
本文实验环境为Windows10操作系统,CPU为Intel Core i7-6498DU双核四线程,其主频为2.60 GHz,内存8 GB.考虑到算法的运行时间也是衡量该算法性能的重要指标,因此将本文提出的APSO-PAA方法和传统PAA方法各运行10次,求取10次程序运行时间的平均值进行对比,表2为两种方法的误差对比情况.
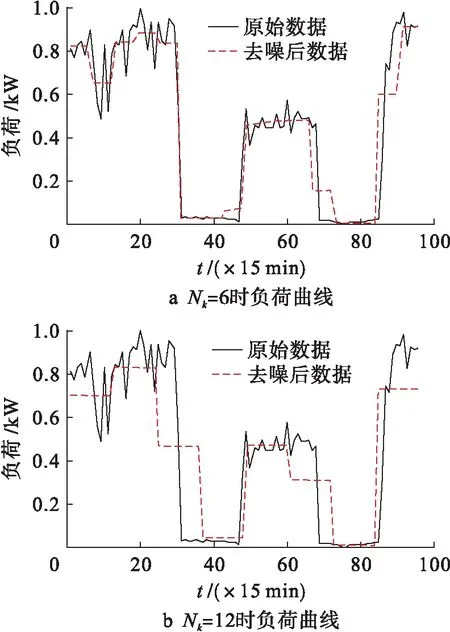
图3 数据样本23在不同压缩比下的分段聚合近似结果
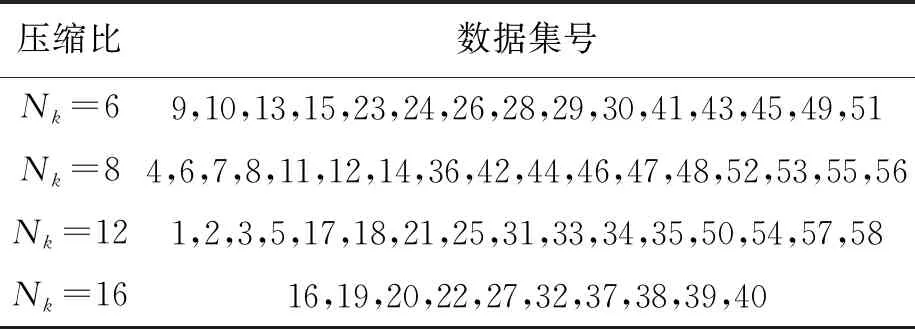
表1 不同数据集对应的压缩比
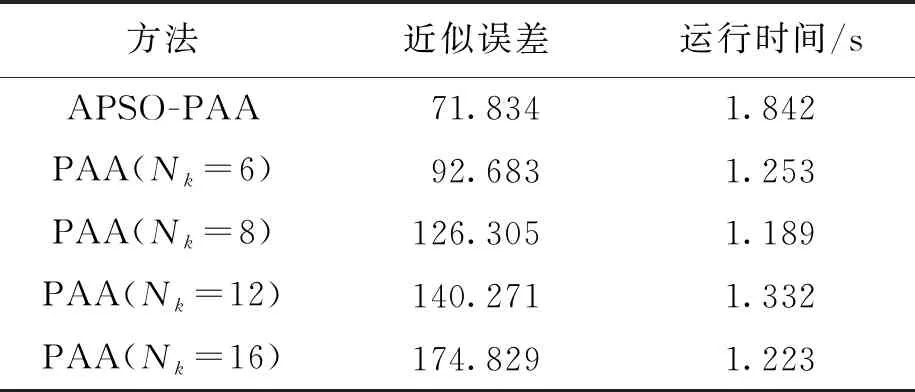
表2 两种方法近似误差比较
由表2可知,本文提出的APSO-PAA算法的近似误差小于传统PAA算法.在压缩比Nk=16时效果最为明显,相比传统PAA算法的近似误差降低了58.92%.其他情况下使用APSO-PAA算法的近似误差分别降低了22.49%、43.13%、48.79%.通过两种算法运行时间的比较可以看出,APSO-PAA算法由于计算步骤较多,虽然在运行速度上做出了牺牲,但是也得到了更高的数据精度.
4.3 负荷数据分类
负荷数据集分别进行PAA和APSO-PAA变换,得到两组不同负荷数据集,再分别对两组负荷数据集进行模糊C均值聚类.为了对比效果明显,本次实验PAA负荷数据集压缩比选取为Nk=12,最优分类数采用本文提出的聚类有效性函数来确定,结果如表3所示.
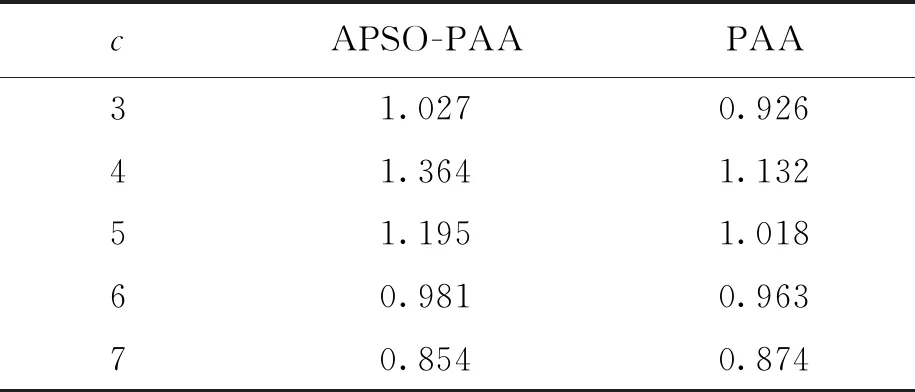
表3 两种方法的有效性指标
从表3中可以看出,对于APSO-PAA变换的负荷数据集,最优分类数为4簇,分类结果如图4所示;对于PAA变换数据集,最优分类数也为4簇,分类结果如图5所示.
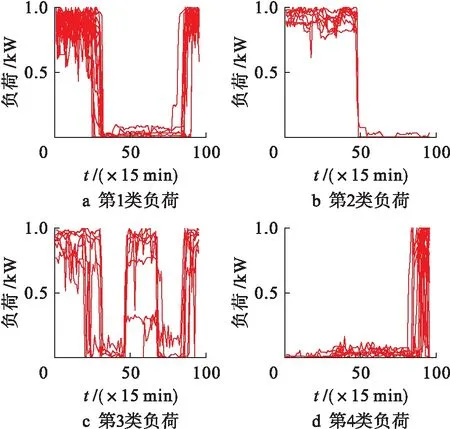
图4 APSO-PAA算法的聚类结果
由图5可以看出,PAA算法在近似表示的过程中,可能会中和掉负荷曲线的平峰、双峰和多峰等形态特征,因此造成在对负荷曲线进行分类的过程中,图5中类别1的双峰负荷混杂了类别3的多峰负荷;类别1中的部分双峰负荷曲线结尾处的突变与波动被中和掉,被划分到类别2中;类别3中的三峰负荷中存在部分前期波动程度较强的平峰负荷.比较图4、5的分类结果可知,本文提出的APSO-PAA近似表示精度要优于PAA算法,聚类效果更明显,有利于实现对不同用电特性负荷曲线的划分.
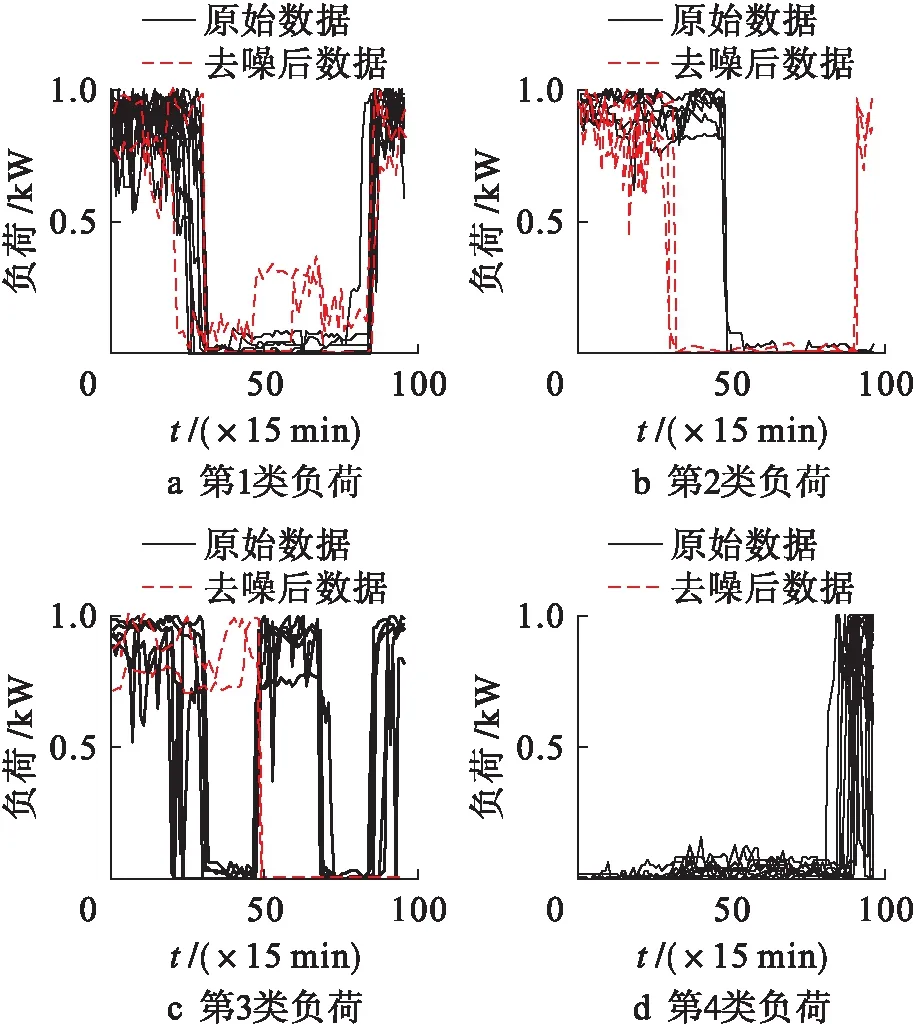
图5 PAA算法的聚类结果
5 结 论
本文选取小波阈值去噪方法降低负荷数据噪声,采用基于粒子群优化的分段聚合近似方法,将负荷数据用基于均值的分段聚合近似方法和适当的压缩比来表示.算例验证表明:
1) 基于粒子群优化的分段聚合近似方法与经典分段聚合近似相比,能够更有效地进行负荷数据降维处理,具有较好的聚类性能和分类结果,算法复杂度低,算法效率高,并且能够获得理想的聚类效果.
2) 基于相似性聚类的负荷分类方法,通过类与类之间的差异性和类内各样本数据之间的相似性来确定最佳聚类数目,实现了负荷曲线的有效分类.
