一类切换连续网络化控制系统的建模与稳定性分析

（北方民族大学，宁夏银川 750030）

网络化控制系统（NCSs）不仅成本低、维护简单，而且实现了资源共享，能有效地实现远程控制和远程诊断。数据通过网络传输与控制系统的融合导致许多新问题出现，如通信延迟、多包传输、带宽限制、时钟异步等。经过几十年的发展，网络化控制系统已经取得了许多关于上述相关问题的研究成果。例如，文献[1]利用滑模控制解决了系统在连续马尔可夫数据包丢包情形下的稳定性分析问题。文献[2]通过将网络化控制系统转换成离散的时间切换系统，解决了闭环网络控制系统的输出反馈镇定问题。文献[3]提出了两种模型来解决宽带受限的网络化控制系统问题。文献[4]讨论了多元化抽样系统的稳定性问题。近期，Cuenca等[5]应用周期事件触发采样和双速率控制解决了无人驾驶飞机的无线网络控制系统的相关控制问题。Yang等[6]解决了一类网络化预测输出反馈控制系统分析与控制问题。Zou等[7]应用事件约束驱动控制解决了非线性二阶多智能体系统的网络化控制系统问题。

本文建立了一类基于电力系统的切换网络化控制模型，分析了该系统的稳定性问题，通过引入适当的切换率，实现了连续子系统之间的切换规则，并保证了系统的稳定性。

1 系统建模

实际的网络化控制系统中，远程控制属于共同特点，如电力传输系统、物联网系统、远程手术操作等。这些系统不断受到各种内部与外部因素的影响，导致系统在信息转换过程中出现不确定性、网络与平面连接不连续等问题，需要在系统和网络之间进行频繁地切换。当开关断开时，即系统与网络断开时，系统可以建模。

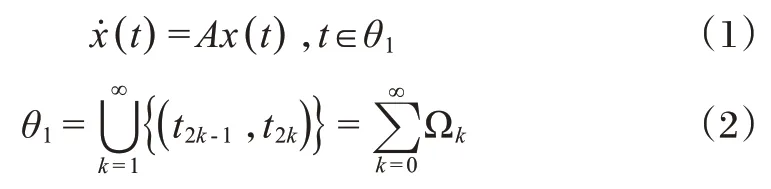
当开关闭合时，即系统与网络连接时，系统可以建模为：

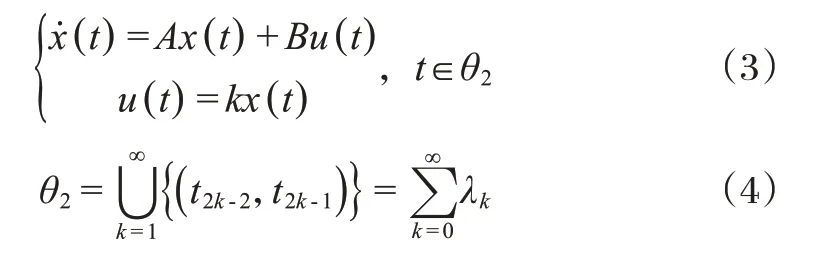
2 稳定性分析

2.1 定理

针对交换网络化控制系统即式（3），如果存在一些标量λi满足:

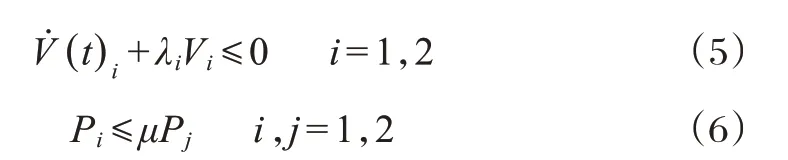
说明系统稳定。

2.2 证明

根据系统，由Lyapunov函数：

当t →+∞时，x(t) →0，所以系统趋于稳定。

3 数值算例

考虑电能传输系统。在每天11：00～14：00和17：00～21：00期间，系统处于功率输出的高峰期，网络化控制此时连接到系统。在剩余时间里，即14：00～17：00和21：00～11：00期间，系统处于功率输出的低谷期，网络化控制此时与系统是断开的。

即：

假设网络化控制系数的系数矩阵如下：

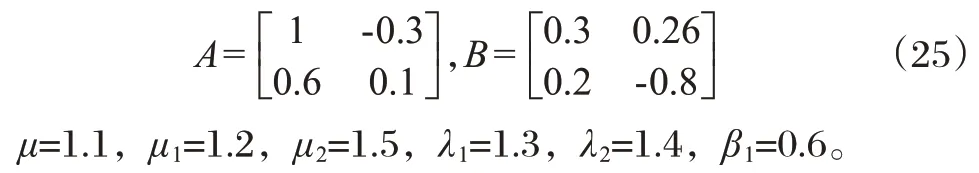
通过求解定理中的矩阵约束条件，得到：

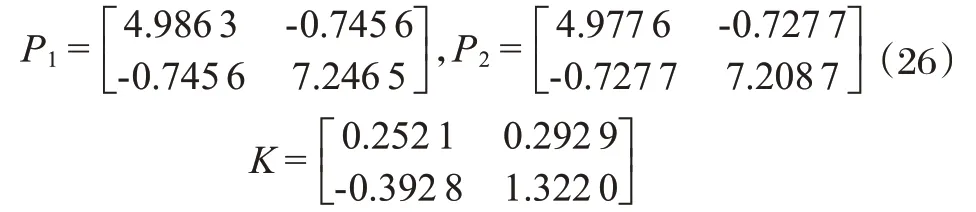
权值状态xT(k)Qx(k)和输出权重zT(k)Qz(k)行为如图1所示。

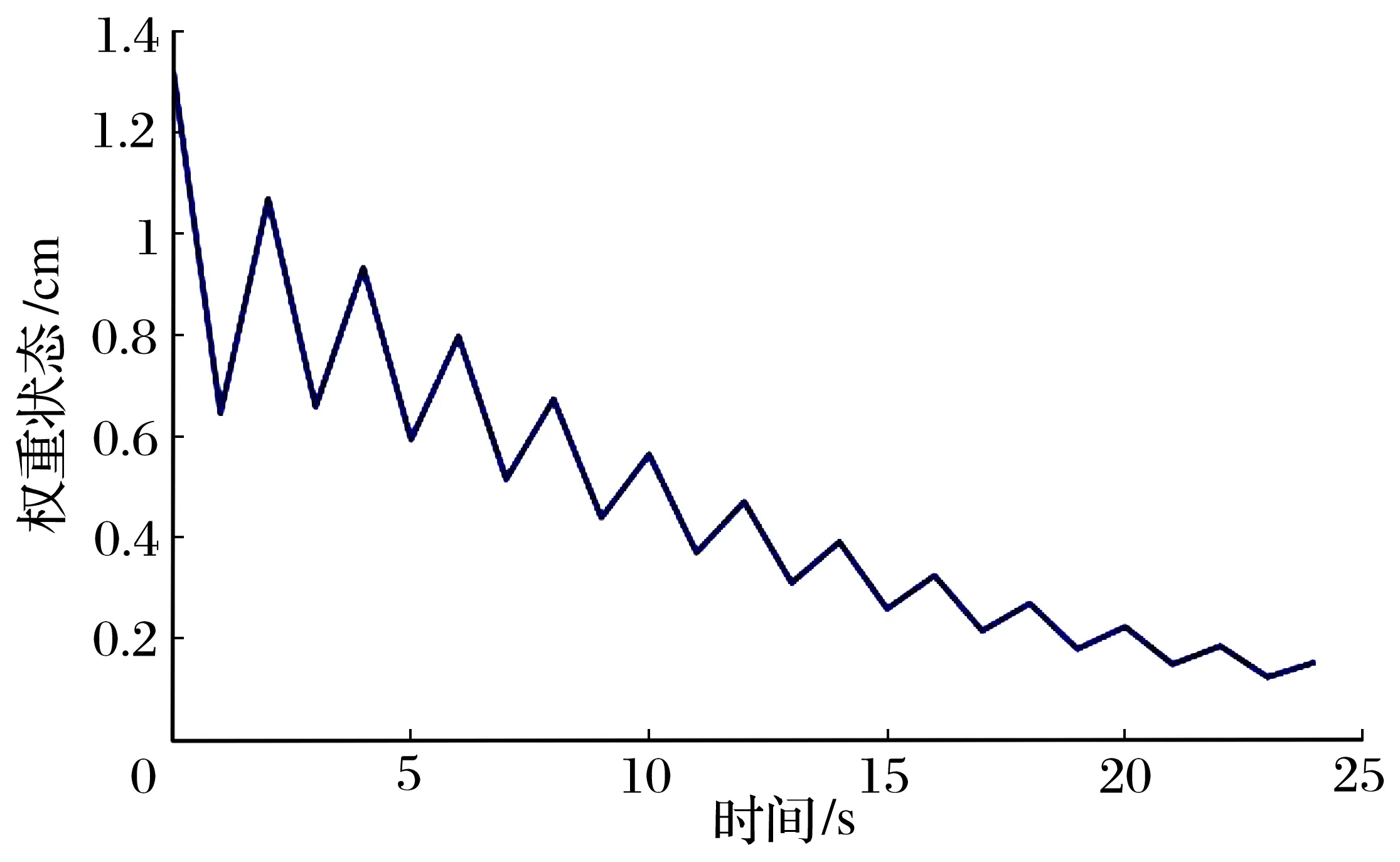
图1 状态权重

通过状态反馈得到了系统输出权重的状态值，利用定理提出的条件，将系统的传动状态成功的控制在了所期望的界内。同样，利用定理得到输出权重，如图2所示。

图2 输出权重

输出权重在利用设计的控制器的情况下，也被控制在了期待的界内。

4 结语

本文以一类电力系统作为研究对象，针对该系统建立了连续型网络控制系统模型。在此基础上，分析了该电力系统的稳定性问题，推得相应的稳定性判据。最后，通过引入具体的电力系统传输电能实例，验证了本文所提判别条件的实用性及方法的有效性。