考虑跌落时相角对幅值特性影响的电压暂降判断方法

刘宇峰，吴学智，2，刘京斗，李晓亮，朱桂棠

（1. 北京交通大学 国家能源主动配电网技术研发中心，北京100044；

2. 北京电动车辆协同创新中心，北京100044；3. 北京星航机电装备有限公司，北京100074）

0 引言

随着电力电子技术的迅速发展，大量新型电力负荷和电子设备得到广泛应用，电能质量问题对于用电设备的危害性日益突出，因此受到国内外学者的关注［1-2］。在常见的电能质量问题中，电压暂降和短时中断已成为最主要的电能质量问题［3-5］。要实现电压暂降的补偿或离网治理，关键是快速、准确地检测出电压暂降特征量，并利用其变化来确定是否有暂降事件发生。

目前，电压暂降的检测方法众多，根据所需特征量的不同，分为峰值电压法、均方根有效值法以及常用的基于dq 变换的幅值电压法等［6-7］，另外，借助数学工具和信号处理手段，也可以快速检测到电压暂降信号，如傅里叶变换法、小波变换法等。峰值电压法通过持续监测半个正弦周期内电压信号的最大值，统计是否有超出或低于正常电压最大值的信号，但采样统计时间较长，不能满足检测实时性要求；均方根有效值法也是对半个周期内的电压信号进行滑动采集，计算均方根值，同样具有延时的缺点［8］。傅里叶变换法与小波变换法的应用场景有限。傅里叶变换法利用短时傅里叶变换，可以准确提取信号的幅值时变特征，但仍存在一个周期的延时［9］；小波变换法利用其对信号奇异点的敏感性，检测暂降的起止时刻，但是对于平滑扰动则无法检测出其结束时间［10］。

幅值电压法是工程上应用较多的方法，其主要原理是基于dq 变换提取瞬时幅值，与提前设置的阈值进行比较得到检测结果。传统的基于瞬时无功功率理论dq 变换的方法只适用于三相对称电压扰动，不能准确提取单相扰动时电压的幅值。现有的dq变换为了适应单相扰动，一般从如下2 个方面进行改进。

（1）利用三相电压的对称关系，通过对已知相电压移相或求导，构造虚拟三相系统，再使用dq 变换得到所需单相电压幅值。如：文献［11］从三相电压对称的角度出发，使用已知单相电压，通过延迟60°构造虚拟三相系统，该方法可以有效检测出电压相位的跳变，但由于虚构的三相电压仍具有不同步性，会造成检测上的延时；文献［12］针对移相法虚构三相系统的延迟，采用对已知相电压求导的方法虚拟其余两相电压，虽大幅缩短了检测时间，但实验中发现对高频噪声的放大作用明显，而且原理不够明确；文献［13］提出基于多dq 坐标系的旋转变换策略，考虑到不对称扰动会使三相系统中产生负序分量，将三相电压分解到不同旋转坐标系下，借用滤波器提取直流分量，该方法可以精确地求解每一相电压的实时幅值，但计算量较大，滤波器的性能直接影响检测效果。

（2）利用已知相电压，通过构造αβ 正交矢量，使用αβ／dq 变换得到单相电压幅值。如：文献［14］利用αβ静止坐标系下uα和uβ之间的关系，将已知相电压延迟90°，构造虚拟正交矢量，直接使用αβ／dq 变换得到检测结果，相比构造三相系统的方法，大幅减少了运算量，但还是存在1/4 工频周期的延迟；文献［15］利用单相电压延迟一定小角度后，构造虚拟αβ坐标系，相比延迟90°的构造方法，实时性得到了改善，也减少了求解的计算量，但是当电压在不同角度下发生跌落时，计算得到的电压幅值会产生一定程度的波动，该过程中再使用实时幅值进行判断会产生误判和延时。

针对上述问题，本文在分析延迟小角度检测法的基础上，理论推导了暂降发生时的电压相位和幅值波动方向的关系，通过预测幅值特征量的变化趋势较快地检测电压暂降事件。该算法可以克服幅值波动对检测的影响，进一步提高检测速度，有利于提升电压暂降治理效果。

1 延迟小角度检测法

电压矢量在αβ 静止坐标系的α、β 轴上的投影可分别记作uα和uβ，可以利用单相电压表达式与uβ相似的特点，构造静止坐标系中的uα和uβ分量［15］。

利用矢量uβ瞬时值与实测电压u1相同的特点，可以设：

其中，U为正常电压幅值；θ=ωt，为电压相位。

将β 轴沿逆时针旋转任意一个角度δ，电压矢量在新的坐标轴上的投影分量记作uδ，其相位滞后于u1，角频率与u1相同，可表示为：

实际离散系统中，可用做表延迟的方法获得角速度为ω、相位一直与待测电压相差δ 角度的uδ：根据角速度ω确定表格长度，并滑动储存u1信息，若系统采样周期为Ts，第k 个周期采样得到的原电压矢量信息为u1(k)，则延迟构造的电压矢量uδ即为n 个周期前的u1信息，计为u1(k −n)，其中n=δ/(ωTs)。

由uδ顶点向uα所在坐标轴作垂线，并与uα反向延长线相交，得到u01和u02，如图1所示。

图1 延迟小角度构造αβ量矢量图Fig.1 Construction of αβ vector with small angle delay

由图1 易得，u01的幅值为Ucos δ，相位与uβ相反，u01=−uβcos δ；矢量u02的幅值为Usin δ，相位与uα相反，u02=−uαsin δ。

根据图1中矢量关系可知u02=u01+uδ，即：

−uαsin δ=−uβcos δ+uδ

进一步可得：

其中，延迟角度δ的大小可调。

dq 坐标系相对于αβ 坐标系以角速度ω 旋转，将uα和uβ转换到dq坐标系下，计算公式为：

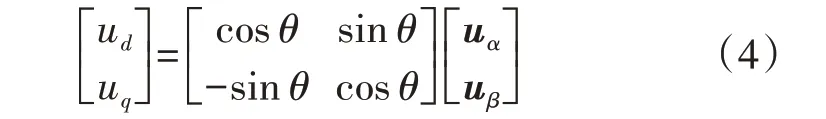
其中，ud、uq为变换到dq 坐标系下的分量。将式（3）中uα和已知电压矢量uβ通过式（4）变换到dq坐标系下，再通过低通滤波器即可得到其直流分量ud0和uq0，基波电压的幅值U0和相位φ 可分别通过式（5）和式（6）计算得到。

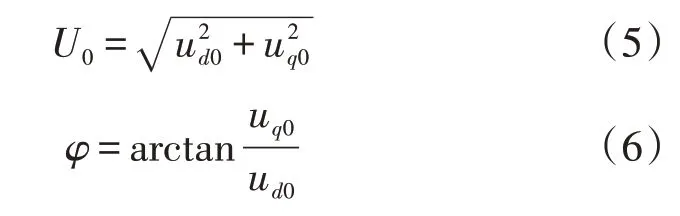
不考虑相位跳变或有谐波干扰的情况下，延迟小角度检测法可以在暂降发生后间隔n 个采样周期，即uδ的幅值能跟踪上暂降后的电压矢量u1时，精确地算出所需幅值特征量。将式（1）和式（2）代入式（3），得到稳态时的uα，结合已知电压矢量uβ，通过式（4）变换到dq坐标系下得到：

由式（7）和式（8）化简可得：ud=U，uq=0。

由上述分析可知，延迟小角度检测法可以在暂降的稳态阶段有效地判断电压暂降。但是由于数据的不同步，在暂降发生后的n 个采样周期内，计算得到的幅值会产生不同方向的波动，该现象会影响检测结果的准确性和实时性，并造成后续补偿的延迟。

2 基于幅值变化趋势的判断方法

针对上述问题，本文首先推算了电压暂降时延迟小角度检测法在dq 坐标系下的幅值特性，由此得到幅值波动的规律，作出正弦曲线；根据该曲线的表现形式，进一步分析了延迟角度δ 对幅值波动程度的影响，通过选择合适的角度，可以改善检测效果；最后，基于以上特征，提出一种改进的电压暂降判断方法。

2.1 暂降时的d、q轴电压特性

在电压发生暂降后的n 个采样周期内，根据算法原理，采样得到的待测电压幅值会瞬时减小，此时设：

其中，U1为暂降的幅值。

由于虚构的电压矢量uδ相位滞后于u1，数据不能同步更新，所以其表达式不变，如式（2）所示。此时的uβ如式（9）所示，uα如式（10）所示。

将式（9）和式（10）代入式（4）可得：

整理后得：

由上述分析可知，在暂降起始阶段，ud与电压相位θ呈余弦函数关系，uq也会有类似规律的波动。

综上所述，由于数据的不同步性，在dq 坐标系下计算得到的分量呈正弦规律变化，幅值计算结果也随之产生波动。

由式（13）和式（14）可知，暂降时刻的待测电压相位会决定接下来n 个采样周期内幅值的波动方向，而延迟角度δ 会影响幅值波动的大小，通过选择合适的δ，可以适当缩短该扰动的持续时间，减小扰动幅度，有利于改善检测精度。

2.2 延迟角度δ的选择

由式（7）和式（13）可知，当系统锁相环实时跟踪待测电压矢量时，待测电压的幅值信息可通过观测ud等效地得到［16］，通过检测该分量对电压暂降进行快速判断。

通过上述分析可知，只要待测电压发生暂降，检测得到的ud都会在n 个采样周期内产生波动，延迟角度δ 决定了n 的大小。令式（13）中的余弦函数部分为：

若ud满足式（16）所示的条件，则可以判断待测电压发生暂降［17］。

由式（13）易知，当发生电压暂降时，暂降幅值ΔU>0.1U，暂降时刻的相位θ 决定了ud的变化方向，且延迟角度δ 选取得越大则ud的变化速度越慢，满足式（16）所需的时间也越长。由于ud的特性曲线呈正弦规律变化，考虑到最恶劣的情况下，在幅值波动期间，若f(θ)>−1一直成立，则系统需要等待幅值曲线稳定，即延时nTs之后，才可以准确判断发生暂降。

下面对这种情景进行仿真，以更清晰地观察延迟角度δ 对检测时间造成的影响。为了保证检测的准确性，设置算法中连续10 个采样周期计算得到的ud均满足式（16）时，才确定发生暂降。

仿真时，设置采样频率为20 kHz，每周期内采集400 个点；δ=0.9°×c，其中c 为正整数；待测电压为标准工频220 V；暂降幅值ΔU=0.5 U。设待测相电压在0.0658 s时刻发生跌落，此时电压相位θ为104°，模拟在幅值波动的上升期，不同延迟角度δ 下的检测过程，如图2所示（仿真中，θ和δ均转换为角度制）。

根据图2 的仿真结果，以式（16）作为判断条件，得到不同延迟角度δ下的检测时间如表1所示。

图2 ud的检测结果Fig.2 Detection results of ud

表1 检测时间Table 1 Detection time

结合图2 和表1 可知，延迟角度δ 越大，则幅值波动时间越长，检测方法的实时性越差。为了更快地获得稳定的电压暂降幅值信息，改善后续补偿效果，δ不宜取太大。

在检测过程中，一方面要考虑检测的速度，另一方面也要保证检测的准确性。若电压信号u1中含有谐波分量，未发生暂降时，设［15］：

其中，U2k1+1、φ2k1+1分别为第2k1+1 次谐波电压的幅值和相位。

根据式（17）延迟后得到uδ，再通过式（3）和式（4）得到此时的ud，整理可得：

其中，uh为检测结果中的交流成分。一方面，δ越小，交流成分越大，检测方法对谐波的放大作用越强，不利于检测的精确度；另一方面，由式（13）易知，δ 越小，ud特性曲线的峰峰值越大，此时若电压只是发生了小扰动，即ΔU ≤0.1U，则也可能在某些相位区间内出现f(θ)≤−1 的情况，系统会将之误判为暂降。为了提高暂降幅值检测的准确性，δ不宜取太小。

综上所述，根据实际电网情况，若谐波含量较大，则需要适当加大δ，同时配合滤波器进行信号处理；若谐波含量较小，可适当减小δ。应用时，可以尝试不同延迟角度，尽量平衡实时性和精确性之间的矛盾。本文在实际设置延迟角度时，综合考虑以上因素，选择δ=13.5°。

2.3 暂降判断方法

根据上述分析，ud是包含幅值信息的正弦函数，通过式（5）计算出的幅值和ud的表现形式类似，将式（13）和式（14）代入式（5）可知结果亦呈现出正弦规律。基于以上特征，在设定好δ 的前提下，本文以ud大小和变化趋势为特征量，提出了一种改进的暂降判断方法。

根据2.2 节的分析，选择δ=13.5°。为了更清楚地介绍新的判断方法，下面将对基于该角度检测得到的ud展开讨论。由于ud波动的周期为π，观测θ∈（0，π）时ud的表现即可。

将δ=13.5°分别代入式（13）和式（15）可得：

f(θ)的曲线可以代表幅值波动期间ud的变化趋势，如图3 所示。可以看出，即使选择了合适的δ，也不能完全避免2.2节中所述的2类问题：当ΔU>0.1U时，若幅值波动期间的f(θ)>−1，式（16）的判断也可能不会立即生效；当待测电压暂降幅值很小，即ΔU ≤0.1U 时，若幅值波动期间的f(θ)≤−1，式（16）的判断可能会生效。

图3 ud的变化趋势Fig.3 Change trend of ud

结合图3，本文提出如下改进策略来解决上述问题。

（1）当ΔU ≤0.1U 且f(θ)≤−1 时，可以将ud(k)−ud(k−1)的值作为约束条件来防止误判，其中ud(k)和ud(k−1)分别为本次和前一次ud的计算结果。当ΔU=0.1U，即式（19）中U1=0.1U时，可得电压发生小扰动时，在幅值波动期间ud可表示为：

若ΔU>0.1U，则有：

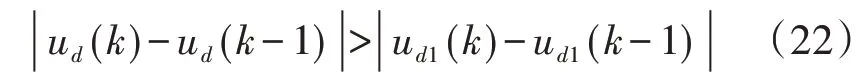
可以对此进行连续几个采样周期的观测，在保证式（22）成立的前提下，使用式（16）对暂降进行判断。

（2）若ΔU>0.1U且f(θ)>−1时，可以通过预测ud在幅值波动期间的变化趋势，对暂降进行预判，缩短判断时间。

根据上述步骤，可以先将一个周期内的电压相位划分为不同区域，同时列写对应的f(θ)的变化趋势，如表2 所示。为了更清晰地表示，将θ 转换为角度制。

表2 不同θ区间内ud的变化趋势Table 2 Change trend of ud under different intervals of θ

结合以上分析，提出新的判断方法如下：

（1）当θ ∈［0°，13°）或θ ∈［141°，180°）时，波动趋势为不断减小，有ud（k）−ud（k−1）<0，且式（22）成立，可判断发生了暂降；

（2）当θ ∈［90°，141°）时，波动趋势为不断增加，有ud（k）−ud（k−1）>0，且式（22）成立，可判断发生了暂降；

（3）当θ ∈［13°，90°）时，直接采用幅值作为判断依据，即ud<0.9U，同时采用式（22）作为约束，确保不会误判。

实际应用时，相位区间的边界对检测结果影响不大，为了避免噪声扰动对检测结果的影响，除了硬件层次的RC滤波，系统还采用了滑动平均法对采样信号进行了滤波，同时需要连续10 个采样周期判断暂降发生的条件是否成立，准确地获得检测结果。检测流程如附录A图A1所示。

3 仿真验证

利用MATLAB 软件按所提出的检测方法对单相电压暂降的判断情况进行仿真验证。三相系统中各相电压均为工频220 V，采样频率设置为20 kHz。为了获得准确的基波正序相位，本文采用响应速度快、滤波效果好的基于二阶广义积分器的锁相环［18］。

在实际工程应用中，动态电压恢复器（DVR）装置要求在任意相电压跌落幅值ΔU>0.1U 的情况下，系统的响应时间不宜大于5 ms［19］，考虑到装置需要时间进行模式切换与电压补偿，暂降判断延时不宜大于2 ms。通过设置A 相电压在不同时刻发生暂降，仿真验证2.3 节中预测的ud变化趋势是否正确；同时，与延迟小角度检测法和延迟90°构造法在暂降判断延时方面进行对比，证明本文检测方法的有效性。

根据系统采样频率，设置δ=13.5°，A相电压分别在0.04 s、0.042 5 s 和0.068 s 时刻发生跌落，跌落幅值ΔU=0.5U，对应的电压暂降时刻相位分别为0°、45°和144°，检测效果分别如附录B 图B1、B2 和图4所示。进一步总结得到3 种方法对电压暂降的判断延时情况，如表3所示。

图4 θ=144°时电压暂降波形及检测结果Fig.4 Voltage sag waveform and detection results when θ=144°

表3 不同检测方法的判断延时Table 3 Judgment time-delay of differentdetection methods

根据以上仿真分析结果，并与图3和表2进行对比，可以得到以下结论：

（1）暂降时刻电压相位不同，延迟小角度检测法得到的ud的变化趋势和大小也会发生改变，附录B图B1（b）、图B2（b）和图4（b）的ud仿真结果均符合表2中对应的相位区间内所记录的变化方向，附录B图B3 同时模拟了电压暂降时刻相位为99°的场景，结果也符合表2的预测结果；

（2）本文所提方法只对延迟小角度检测法的暂降判断依据进行了改进，并没有改变其幅值或相角的检测原理，由图4（b）可知，本文方法可以快速得到暂降后稳定的幅值信息，而延迟90°构造法检测得到的幅值需要等待5 ms左右才能稳定；

（3）由附录B 图B1（c）、图B2（c）和图4（c）可知，本文方法的判断延时较小，一直保持在2 ms 以内，可以满足DVR 工程的需求，而延迟小角度检测法和延时90°构造法的判断延时会随电压暂降时刻相位的不同而改变，可能会不满足工程需求；

（4）由表3 可以直观地看到，本文方法的实时性优于其他方法，且不会随电压暂降时刻相位的不同而改变。

为了进一步体现本文方法的优点，可以根据2.3节中提出的2 种特殊情况，对延迟小角度检测法和本文方法进行仿真并对比分析检测结果。

（1）若电压暂降时刻相位满足f(θ)≥−1，则使用延迟小角度检测法时的判断延时较大。

设置A 相电压在0.065 5 s 时刻发生跌落，跌落幅值ΔU=0.5U，电压暂降时刻相位为99°，检测结果如附录B 图B3 所示。可以看到，本文方法可以克服幅值波动影响，较快地判断暂降事件；而采用幅值大小作为判据的延迟小角度检测法需要在暂降稳态期间才生效，判断延时较大。

（2）若电压产生小扰动，延迟小角度检测法所使用的幅值判据可能会误判。

设置A 相电压在0.062 5 s 时刻有小扰动，跌落幅值ΔU=0.05U，电压暂降波形与附录B图B2（a）相似，对比延迟小角度检测法和本文方法的检测效果，如图5所示。由图可知，由于延迟小角度检测法的放大作用，在ud波动期间，系统可能会误判，而本文方法可以适当提高暂降检测的准确度，避免扰动对检测的影响。

图5 检测结果对比Fig.5 Comparison of detection results

4 结论

针对延迟小角度检测法的缺点，本文提出了一种改进的电压暂降判断方法，通过分析已有方法在暂降时刻的d、q 轴电压特性，总结出幅值变化规律，据此可以提前预测幅值变化趋势，进一步得到暂降判断结果。

该方法原理简单，推导过程清晰，在实际工程中易于实现；相比于传统的基于幅值大小判断暂降的方法，可以避免小扰动和幅值波动对检测的影响，提高了检测准确度和实时性；根据实际电网情况，可通过选择合适的延迟角度δ 来改善检测效果。通过在仿真环境下对不同时刻电压暂降检测的模拟，对本文方法进行了验证，同时与已有方法进行了对比，结果表明了本文方法的有效性。

附录见本刊网络版（http：//www.epae.cn）。