部分浸水周向开口圆柱壳声散射特性研究
2021-03-29屈凯旸
屈凯旸,王 斌,2,范 军
(1.上海交通大学高新船舶与深海开发装备协同创新中心海洋工程国家重点实验室,上海200240;2.哈尔滨工程大学水声技术重点实验室,哈尔滨150001)
0 引 言
随着低频大功率主动声呐和声制导反舰鱼雷智能化的发展[1],水面舰船的回波特性越来越受关注,蕴含其中的水面舰船线型、结构、尺度、航速等信息是主动声呐探测与识别的重要依据[2]。水面舰船回波的物理本质是界面附近目标声散射问题。汤渭霖教授提出了沉底水雷声散射三亮点模型[3],该方法在水面附近目标的散射特性研究中同样适用[4]。而关于流体中圆柱壳的声特性,国内外很多学者也曾做过大量研究。Junger[5]对流体中简单结构(例如球体、柱体、板等)的声散射问题进行了权威、细致的论述;何祚镛[6]较系统地讨论了无限长、有限长与周期加肋圆柱壳的声振特性;范军和刘涛[7]较深入地研究了水中圆柱壳结构的声散射现象;叶文兵[8]研究了不同浸没状态下完整圆柱壳结构的远场辐射声压与输入能量流;张明敏[9]计算了端面开口的有限长圆柱薄壳的辐射声场问题。目前对于水中圆柱壳声散射的研究工作主要是在全自由域条件下对完整柱壳模型进行分析,鲜有在半无限空间中对周向开口圆柱壳结构的研究。本文开展了半无限空间周向开口圆柱壳声散射建模与机理研究,分析了散射声场变化规律及其主要影响因素。
1 理论建模
假设圆柱薄壳沿轴线方向为无限长,平面波垂直入射,柱模型在二维下展开讨论[10]。设定圆柱壳轴心与水面重合,以w和v来分别代表壳体径向与周向位移。如图1 所示,采用参数φ1来表示壳体开口弧度的一半,并用h与a来分别代表壳体厚度与半径。壳模型材料的杨氏模量为E,泊松比为μ,密度为ρ。
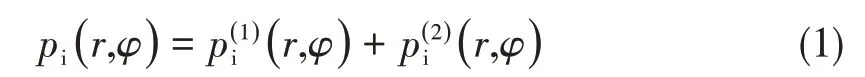
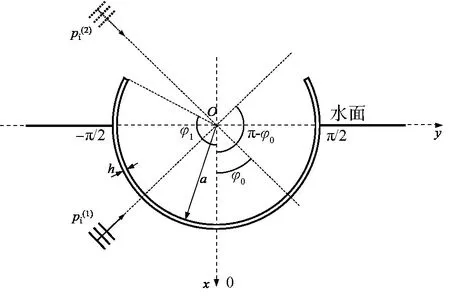
图1 周向开口圆柱壳示意图Fig.1 Tangentially-open cylindrical shell
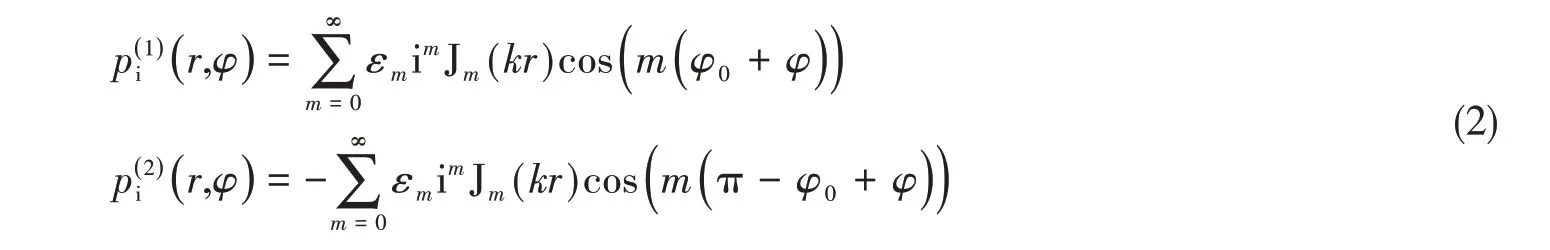
对应的散射声场分别表示为

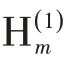
采用薄壳理论,由Donnell方程可以得到[12]
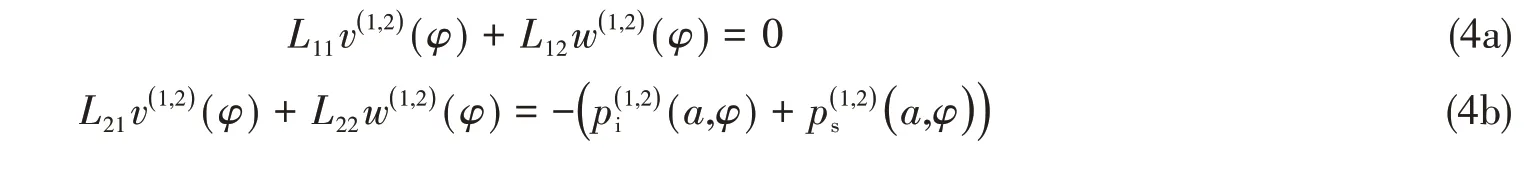
式中,[L]元素见附录A。
壳体法向、切向位移可以表示为
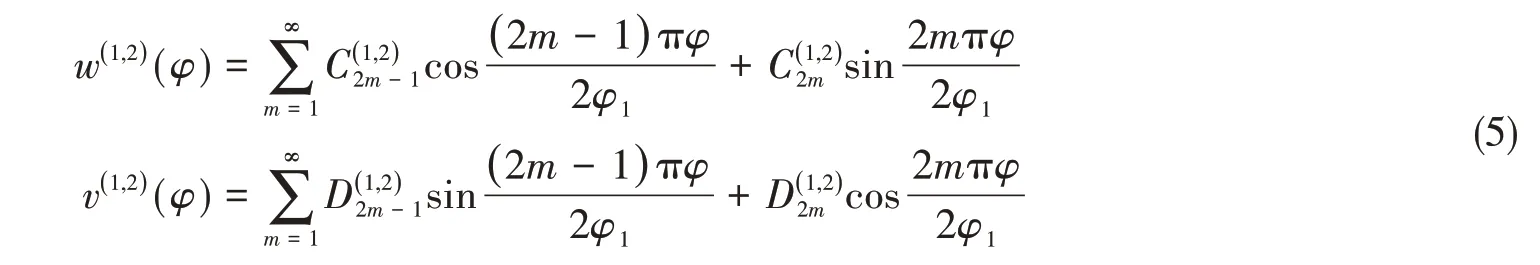
壳体表面满足位移连续条件,即

若式(6)等号右边为零,即为刚性圆柱壳声散射。

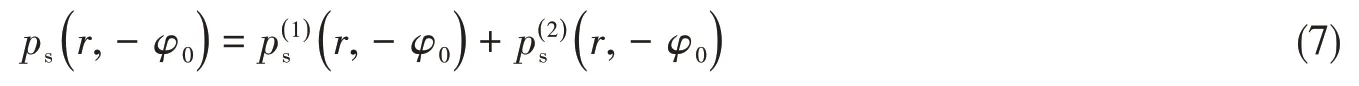

图2 浸水开口圆柱壳柱表面反向散射示意图Fig.2 Backscattering diagram of immersed open cylindrical shell column
2 部分浸水刚性开口圆柱壳体声散射
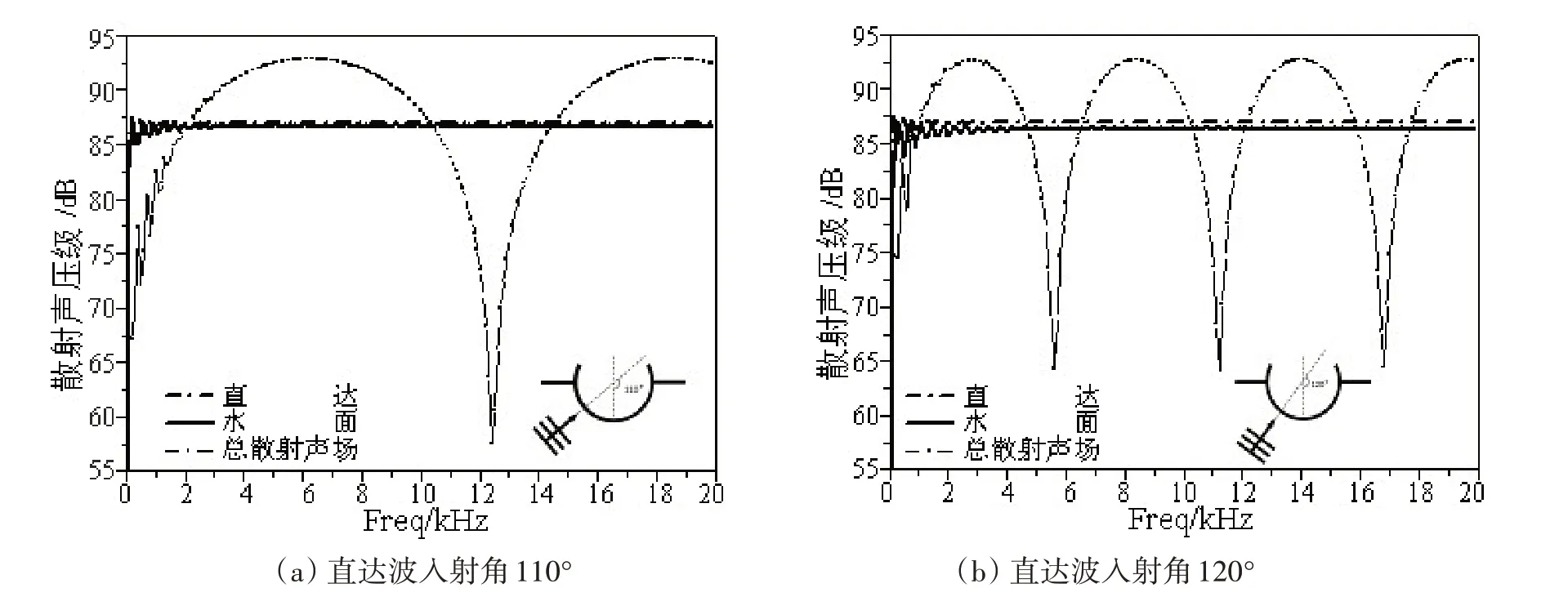
图3 部分浸水刚性开口圆柱壳体反向散射声压级随频率变化Fig.3 Backscattering sound pressure level of a partially-impregnated rigid open cylindrical shell versus frequency
从图3可以看出:
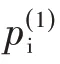
(2)总反向散射声场由直达入射波或水面虚源入射波引起的反向散射声场叠加形成,随频率变化呈现明显增强和抵消的干涉现象,不同入射角干涉周期随频率变化不同,入射角越大频率干涉间距越小。在高频远场条件下,图2中亮点1和亮点2散射波到达接收点的声程差为

相对应可以得到亮点1和亮点2在接收点形成的干涉效应,其干涉频率为
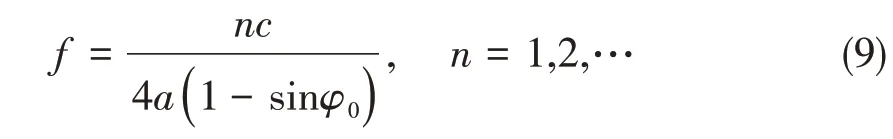
当n 为奇数时总散射声场相互干涉增强,当n 为偶数时总散射声场相互干涉抵消。
图4 给出了部分浸水刚性开口圆柱壳体反向散射声压级随频率f 与入射角π - φ0变化伪彩图。图4 中明显出现了强弱相间的干涉条纹,这些干涉条纹对应上述的亮点叠加干涉现象。图中实线与虚线是由公式(9)给出的干涉频率近似结果,近似结果与计算得到的干涉条纹吻合较好。并且值得注意的是,图4 更为明确地给出了不同入射角干涉周期随频率变化不同,入射角越大频率干涉间距越小的规律。
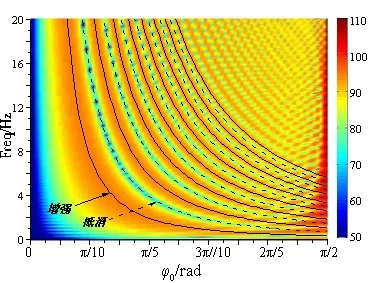
图4 反向散射声压级随频率f与入射角变化Fig.4 Backscattering sound pressure level as a function of frequency and angle of incidence
3 部分浸水弹性开口圆柱壳体声散射
本章讨论部分浸水弹性开口圆柱壳体反向声散射。开口圆柱壳体半径为1 m,壳体半开口角φ1分别为120°和150°,水面虚源入射波方向角φ0分别为70°和60°,直达入射波方向角π - φ0分别为110°和120°,计算得到的反向弹性散射声压级随入射频率关系如图5所示。

图5 小掠射角入射时背向散射声压级随频率变化规律Fig.5 Variation of backscattering sound pressure level with frequency with a small glancing angle
从图中可以看出,圆柱壳体弹性散射曲线之上叠加了特征明显的共振峰,共振峰的位置与幅度随着平面波入射角度与柱壳壳体结构半开角的变化而发生改变。
利用弹性环绕波传播模型对共振现象展开分析。虽然壳体开口,但是壳体上波的类型和传播速度与封闭情况一样。在入射平面波的作用下,无限长圆柱壳体表面的振动情况与z轴无关。此时的波只沿圆周方向环绕,如图6 所示。周向开口处(B和B’)可等效为弹性表面波传播的反射面。入射角等于临界角θc的入射声线在图6 中圆柱上A 点激发起表面绕行波,最低阶绕行波从A 点开始绕壳体传播不足一周(A→B→B’→A’)就产生反方向的回波,同时继续绕行直至增加一周后再一次产生回波。如此不断循环形成环绕波。

图6 平面波垂直入射到无限长圆柱激发的环绕波及其再辐射Fig.6 Surrounding wave excited by plane wave striking infinitely-long cylinder at a perpendicular angle and its re-radiation

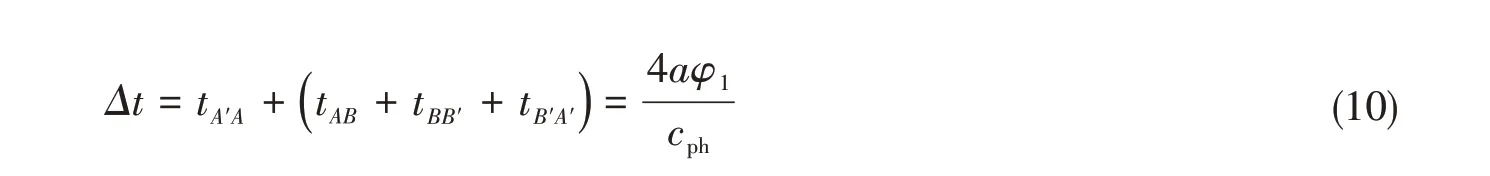
由此可以得到圆柱表面环绕波的共振条件为




图7 为远场100 m 处的开口角度-频率-远场弹性波散射声压级伪彩图,其中横坐标为开口角度,纵坐标为入射平面波频率,弹性散射声压级用颜色深浅来表示。在伪彩图上叠加了由式(13)绘制的黑色s0波频率-角度曲线。
观察发现,黑色s0波频率-开角曲线与伪彩图亮线在高频时吻合情况较好;同一条s0曲线上声压交替呈现抵消与增强,说明壳体表面的共振在远场处与入射波产生了相互干涉叠加与相互干涉抵消;圆柱壳半开口角度越大,散射声场的频率干涉间距就越小。

图7 不同频率不同开角的远场声场情况(a=1,r=100)Fig.7 Far field sound field with different open angles at different frequencies (a=1,r=100)
图7(a)和7(b)分别表示正横方向和斜向上120°入射下情况。有若干条纹自左上至右下划过整幅图像。而这些亮条纹较好地预测了式(13)中不同阶次n下的频率-开角曲线,未完全吻合的原因是引入的圆柱薄壳弹性波理论是在真空条件下的,因此与流体中的结果稍有出入。另外,图7(a)中伪彩图只预测出了当n为奇数时的s0波频率-开角曲线,而图7(b)预测出了全部的s0波频率-开角曲线,这是因为在振动和声学中,如果有对称性发生,模态会发生兼并。当入射波从正横方向入射时,圆柱壳产生左右对称的振动,与此同时水面对壳体振动的影响也是左右对称的,在这种情况下圆柱壳的偶数阶次的振动会相互抵消掉,因此会出现s0波曲线间隔湮灭的现象,表现为图7(b)的两条亮纹间的一条亮纹于图7(a)中消失。
4 结 论
本研究建立了部分浸水开口圆柱薄壳声散射模型,将直达入射波和水面反射波激发下目标散射声场进行了分离。研究结果表明:
(1)总反向散射声场由直达入射波或水面虚源入射波引起的反向散射声场叠加形成,随频率变化呈现明显增强和抵消的干涉现象。不同入射角干涉周期随频率变化不同,入射角越大频率干涉间距越小。
(2)中低频下,半浸圆柱壳的刚性目标声散射处于瑞利区和菲涅尔区,反向散射声压随频率变化呈现振荡现象,随着频率升高逐渐进入散射光学区,振荡幅度逐渐变小。入射角增大时,亮点散射截面减小,水面虚源入射波引起的散射声压级有所降低。
(3)半浸开口圆柱壳开口处对弹性环绕波s0波共振有影响。s0波引起的共振对散射声场影响较大,引起了明显的频率干涉条纹,这与圆柱壳半径和开口角度有关。圆柱壳半开口角度越大,散射声场的频率干涉间距就越小。

附录B

式中,

式(4a)分别乘以cos 2mπφ2φ1和sin ( 2m - 1 )πφ2φ1在区间(-φ1,φ1)进行积分,整理得到
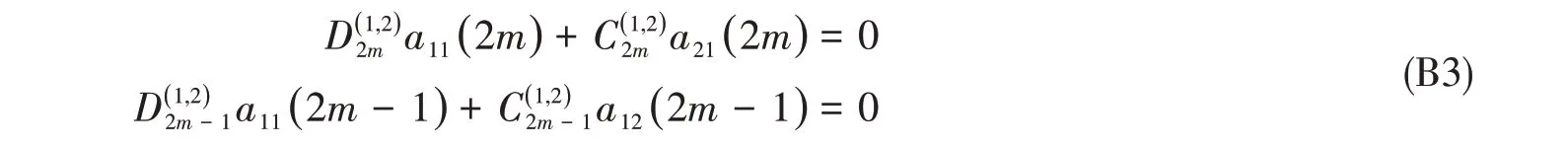
式中,a11,a22,a12和a21见附录C。
式(4b)分别乘以sin 2mπφ2φ1和cos ( 2m - 1 )πφ2φ1在区间(-φ1,φ1)进行积分,得到
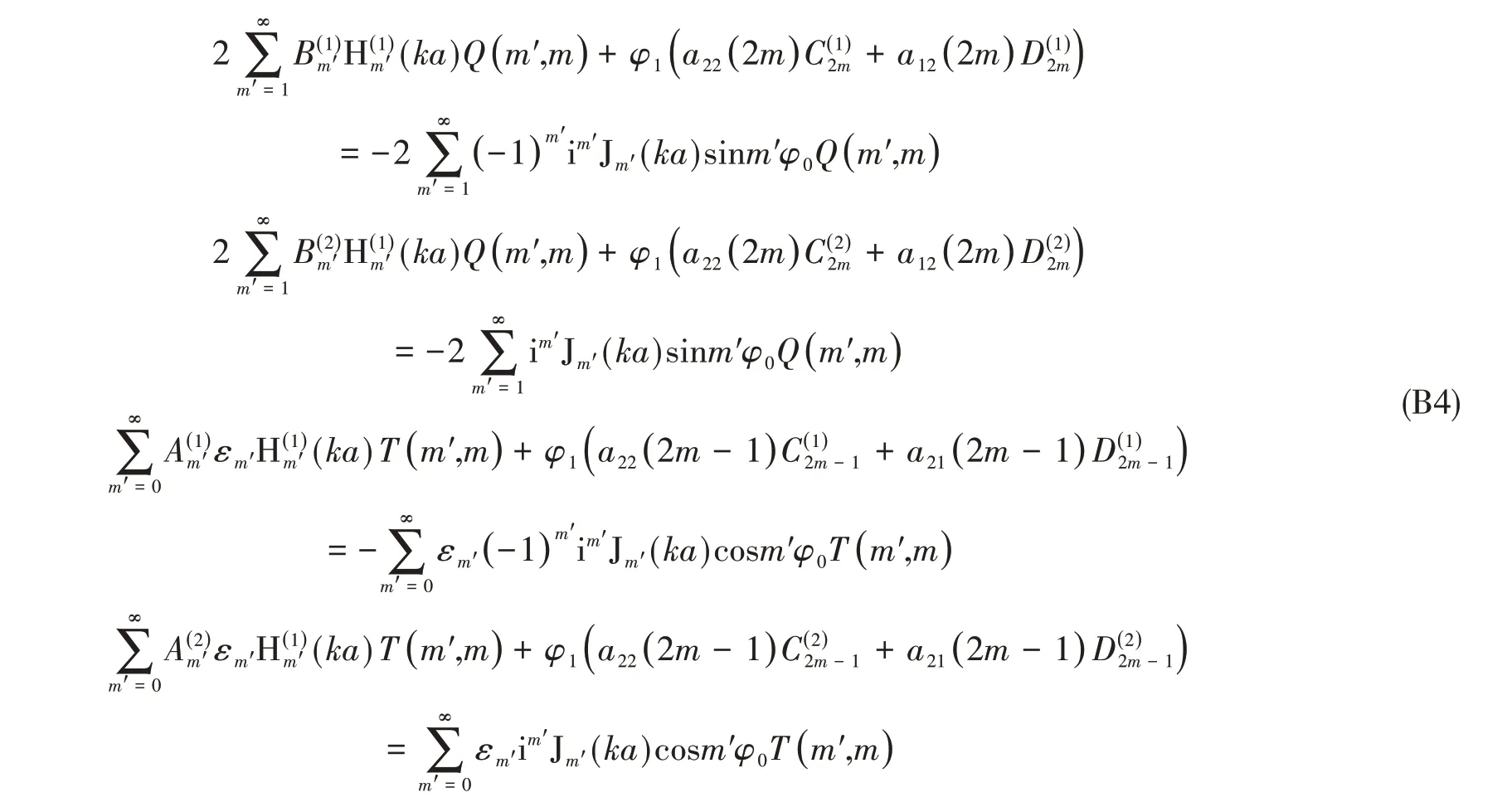
联立式(B1)、(B3)和(B4)可以得到

附录C

