桂林岩溶石山常绿落叶阔叶混交林种-面积曲线研究

解婧媛，利恒春，向珊珊，姜 勇

(广西师范大学 生命科学学院；珍稀濒危动植物生态与环境保护省部共建教育部重点实验室，广西 桂林 541004)

0 引 言

在野外调研植物群落生态学时常因为各种原因无法对一个群落进行全面调查，因此调查某一群落的物种组成等生态学问题常通过取样调查方式进行植物群落研究[1-2]。若想科学地进行植物群落的取样调查，取样面积应足够体现该植物群落的基本特征，同时又不致资源浪费，应提前知晓体现这个植物群落基本特征的最小面积[3-4]。植物群落的最小面积是体现该群落类型种类组成及真实结构特征的面积，即某个特定类型群落能充分、自足地生存所需的面积[5]。

目前，普遍用来确定植物群落最小面积的方法是种-面积曲线法(或称为种-面积关系法)，也就是在慢慢增大样地面积时，统计样地内的物种数，根据数据绘制出对应的种-面积曲线图，在该曲线形式出现变化(不再上升或缓慢上升)时所对应的面积即为该植物群落的最小面积[6]。种-面积关系的概念是由Candolle和Jaccard两位学者最早提出[7-8]，描述的是植物群落中物种数目随面积的增加而变化的规律，是群落学调查中非常重要的内容[9]。运用种-面积曲线可确定合适的取样调查强度、比较不同面积条件的多样性、合理选择生物多样性的保护优先区[10-11]、估算因物种生存环境丧失导致生物多样性降低[12-13]、评判人类活动对植物生态系统多样性的影响[14]等，因此种-面积曲线对生物多样性的评价及保护具有重要的参考意义。

桂林岩溶石山区是全球演化最典型的岩溶发育区，位于中国西南喀斯特地区，在岩溶石山生态系统中极具研究价值。该地区物种资源较为丰富，地表生态类型复杂，但同时也存在生态系统抵抗力薄弱问题[15-18]，且桂林岩溶地区因其独特的地质背景，地形破碎，地表水缺乏，生境异质性强，难以抵抗外界干扰，加上人类的干涉与破坏，该区域原生植被日益减少，生态前景不容乐观。因此，进行桂林岩溶地区的生态修复与重建，保护桂林岩溶地区植被资源成为亟待解决的问题之一[19]。对桂林岩溶地区进行生态修复与重建必须要明确群落种类组成，而研究植物群落、进行样地调查时，明确植物群落的最小面积[20]，并进行一个地区的物种数与其面积分布规律研究，对该地区生物多样性维持及其物种保护也具有重要的指导意义[21]。

近年来，许多学者致力于桂林岩溶区的生态学调查，然而，目前关于桂林岩溶地区植物群落最小面积的研究尚未见报道，鉴于此，将桂林岩溶石山常绿落叶阔叶混交林植物群落作为研究对象，讨论该地区常绿落叶阔叶混交林的种-面积曲线，揭示桂林岩溶石山植物群落最小面积的变化规律，为桂林岩溶石山植物群落调查及物种多样性提供理论基础和研究依据，促进桂林岩溶区的植被恢复工作。

1 材料与方法

1.1 研究区概况

研究区位于广西壮族自治区桂林市区东北部和灵川县东部的灵田镇小水村后山(110°25′10.36″～110°25′40.38″ E，25°19′04.52″～25°19′07.22″ N)，是较为典型的岩溶地貌区。该区属于中亚热带湿润季风气候，全年光照充足，气候温暖，降雨和高温出现在同一时期，年均降雨量为1 949.5 mm，4～7月多降雨，秋冬季则干燥少雨，年均温为18℃～19℃，1月(最冷月)平均气温为7.9℃，8月(最热月)平均气温为28℃，全年平均风速为2.2～2.7 m/s。该地区地表破碎，形态复杂多样，成土速度慢且岩溶地貌特征显著。土壤颜色主要是黄棕色或黑色，且土层具有不深不厚、岩石裸露程度高、土壤干燥、含有较多钙等特点。受这些特殊环境条件影响，适合在该地区生长的植物多为喜好钙性土和石灰性土、耐干旱的植物。在桂林灵川县灵田镇小水村后山地区，由于靠近居民区，在人为活动干扰及自然因素的双重影响下，该地区原生植被受到严重损害，现存植被以次生的亚热带常绿落叶阔叶硬叶林为主，主要优势种有粗糠柴(Mallotusphilippensis)、青冈栎(C.glauca)、光皮梾木(Cornuswisoniana)、红背山麻杆(Alchorneatrewioides)、檵木(Loropetalumchinense)、菜豆树(Radermacherasinica)等。

1.2 研究方法

1.2.1 样方建立和群落学调查

选取桂林市灵川县灵田镇小水村岩溶石山地区受人为干扰比较轻且保存相对比较完整的常绿落叶阔叶混交林作为研究对象，在研究区内建立一个(320×60 m)固定样地，将其划分成48个20×20 m的连续样方，从低海拔至高海拔标记为样方1、样方2、……、样方48。再将每个20×20 m的样方划分为16个5×5 m的小样方，记录每个小样方内胸径≥1 cm 的所有木本植物的种名、多度、基径、胸径、树高、空间坐标与死亡状况等。

1.2.2 种-面积关系的确定

Azovsky认为，取样方法对种-面积关系的影响显著[22]。姜俊等在研究吉林蛟河针阔混交林样地的最小面积时，也证明取样方法对种-面积关系影响不可忽视，且得出随机样方法可降低物种集群分布的影响，拟合效果要比巢式样方法更优[21]。只对不同面积大小的样地进行一次观察是不可靠的，应依据物种数目的变异量来决定所需的样方数量，并且小样地中的变异尤为明显，因而小样地应尽可能多取一些[23]，并通过多次抽取计算均值的方式降低随机取样可能会造成的物种缺失，进而增加统计可靠性[24]，因此利用随机取样法构建种-面积关系。

在给定区域内随机按照取样面积为25 m2、100 m2、225 m2、400 m2、625m2、900 m2、1 225 m2、1 600 m2、2 025 m2、2 500 m2、3 025 m2、3 600 m2、4 225 m2、4 900 m2、5 625 m2、6 400 m2、7 225 m2、8 100 m2的方式逐步扩大面积，依次统计不同取样面积下对应的物种数量，再通过软件R.3.4.2对每一取样面积下的物种数进行999次sample抽样(随机抽样)后算均值，此值就是该取样面积下的物种数。以25 m2取样面积为例，在19 200 m2(320 m×60 m)固定样地内，共可以划分出768个25 m2的小样方，分别统计这768个小样方的物种数，对这768个小样方进行999次sample抽样物种数后求均值，即为25 m2内的物种数，以此类推，得到所有数据，作实际种-面积曲线。

另外，研究中常通过模型来拟合种-面积曲线，从而确定理论群落最小面积。进行种-面积曲线拟合所用的模型方程主要是非饱和(unsaturation)曲线、饱和(saturation)曲线[25]。利用以下8种模型来拟合桂林岩溶石山常绿落叶阔叶混交林的种-面积关系(见表1)。其中，A表示取样面积，S表示该取样面积A中的物种数，c、z、f为模型中的参数。

表1 种-面积关系候选模型

评价模型拟合优度的标准有多种，本研究采用赤池信息量准则(AIC值)来对种-面积曲线模型的拟合优度进行评价。AIC准则中，公式的前一部分体现模型的拟合精度，后一部分体现模型中有几个参数，即同时考虑样本量和参数个数，模型拟合得越好，AIC数值就越小，这样才能得到准确的预估值[26]。

数据处理及作图采用Microsoft Exel.2010和R.3.4.2软件处理。

2 结果与分析

2.1 实际种-面积曲线

根据实地调查数据作出实际种-面积曲线图，由图确定最小面积的方法是最快捷简单的[3，6]。通过实测数据得到取样面积与物种数结果如表2，并由此得种-面积曲线，见图1。

表2 不同取样面积的物种数

物种数目随取样面积扩大而有规律地增加，起初增加幅度很快，以后逐渐缓慢。曲线在取样面积为2 000 m2时出现了拐点，2 000 m2以后物种数目缓慢增加，趋向稳定，因此根据实际种-面积曲线得到桂林岩溶石山常绿落叶阔叶混交林的最小面积应在2 025 m2左右，见图1。

2.2 种-面积曲线的拟合

采用8种曲线模型对桂林岩溶石山常绿落叶阔叶混交林种-面积关系进行拟合求解，结果如表3所示。

由表3的拟合结果可知，尽管8个模型拟合的R2值均达0.9及以上，但从AIC值来看，各模型的拟合结果存在较大差异，其中(1)幂函数模型的AIC值最大为72.583 4，拟合效果最差，(6)逻辑斯蒂模型、(3)负指数函数、(2)指数函数这3个模型的AIC值分别为60.620 2、54.367 4、48.998 8，拟合效果也不够理想。模型(4)莫诺模型、(5)有理函数、(7)洛莫利诺模型、(8)累积韦伯分布模型的AIC值都低于30且较为接近，说明这4个模型的拟合效果较好。但评价种-面积曲线模型时不能只观察模型的统计学结果，一方面模型需能体现物种数目随样地面积变化的规律，另一方面，该模型还应符合清晰的生物学意义[27]。卓茜[28]等结合前人的研究指出以下判断种-面积曲线是否具有生物学意义的重要依据：第一，Buys等认为物种数目与样地面积的关系必定符合非减函数趋势。第二，面积逐渐扩大时，物种数目不应该是无限值。第三，刘灿然等人还指出种-面积曲线的纵截距不大于0，对应的横截距不小于0[27-29]。

根据上述依据，从图2和图3来看，这8个模型均为非减函数，符合物种数目随着面积的扩大而增加的规律，满足第一点。(1)幂函数模型和(2)指数模型的曲线并无渐近线，即模型可能呈无限增长，在给定区域内物种数目并非有限，尤其是在大尺度的研究上可能导致对物种数的严重高估，不满足第二点。而(6)逻辑斯蒂模型和(7)洛莫利诺模型的曲线纵坐标轴有正截距，即当面积=0时便有物种的出现，这显然不符合实际，不满足第三点。模型(3)(4)(5)(8)均满足三点依据，具有良好的生物学意义，但是限制的条件太多时，可能会使拟合模型的曲线拘泥于数学形式，降低其灵活性，导致出现不良拟合效果[27]，因此在符合生物学意义的基础上，综合模型拟合的评价指标AIC值来看，可见模型(3)的拟合效果较差，拟合效果较好的为模型(4)(5)(8)，而其中(8)累积韦伯分布模型的AIC值最小(23.858 5)，即在满足三点生物学依据的基础上拟合效果也最好，因此可得出桂林岩溶石山常绿落叶阔叶混交林的最优种-面积曲线模型为累积韦伯分布模型(cumulative Weibull)，方程为：

图2 模型1、2、6、7拟合曲线

图3 模型3、4、5、8拟合曲线

S=73.801 7(1-exp(-0.013 8A0.668 5))

据此方程得到的最优拟合模型曲线如图4。

图4 最优拟合模型累积韦伯分布模型

2.3 群落最小面积的确定

目前，生物学界通过拟合曲线模型求解群落最小面积方法不少，研究主要通过群落总种数比例法[30]与二阶导数法求取[31]。

2.3.1 群落总种数比例法求取最小面积

群落总种数比例法需要确定比例因子ρ(0<ρ<1)，即取占群落总种数该给定比例ρ的物种数时所需要的最小面积。对最优模型累积韦伯分布模型S=c(1-exp(-zAf))用此法，所需的最小取样面积为：

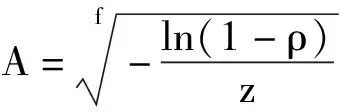
(1)

唐龙等认为，在群落调查中，比例因子ρ不一样得到的最小面积也不同，因此可根据法国CEPE规定，群落最小面积即为含有84%物种数的样地面积[31]，因此比例因子ρ取0.84，把累积韦伯分布模型参数z=0.013 8、f=0.668 5代入公式，可得桂林岩溶石山常绿落叶阔叶混交林最小面积为1 499 m2，即当最小面积取1 499 m2时能满足精度84%的研究要求。

2.3.2 二阶导数法求取最小面积

对最优模型累积韦伯分布模型S=c(1-exp(-zAf))采用二阶导数法，求得其二阶导数为：

S=-(8839692504061843384974069exp(-(69A^(1337/2000))/5000))/(1407374883553280000000000000A^(663/1000))-(63528732184243354299999exp(-(69A^(1337/2000))/5000))/(281474976710656000000000A^(2663/2000))。

S″为0的点所对应的A即为最小面积。但由累积韦伯分布模型得到的S″-面积曲线为递增的凸函数,不存在真正的拐点，而其极限为0的点变化增量趋向于0，因此近似地取其为拐点[31]。由二阶导数-面积曲线图(图5)可以看出，当面积为2 500 m2时，S″值趋近于0，因此，可将2 500 m2作为桂林岩溶石山常绿落叶阔叶混交林的最小面积。

图5 二阶导数-面积曲线

2.3.3 群落最小面积的比较与确定

由实际种-面积曲线得到的最小面积为2 025 m2。对比通过最优模型累积韦伯分布模型求取最小面积的两种方法，由群落总种数比例法求解的最小面积为1 499 m2，由二阶导数法求解的最小面积为2 500 m2，可以看出群落总种数比例法得到的最小面积要比实际调查得到的最小面积小得多，而通过二阶导数法所求的值比实际调查情况稍大，这是因为群落总种数比例法采取的思路是：在种-面积曲线可以完全地、准确地反映该植物群落所有特征的情况下，此植物群落的所有物种数能先通过该曲线(species-area curve)被预估出来，并据此总种数计算所需最小面积，但这样有可能会造成对物种多样性过低的估计，因为仅由小尺度的种-面积曲线推出大尺度地域的物种多样性时，总是要受到缩尺效应、区域相互分化而产生的差异等影响[32-33]，因此利用二阶导数求取最小面积的方法更具有科学性，这与卓茜等[28]的研究结果一致，根据此法求得的桂林岩溶石山常绿落叶阔叶混交林的最小面积为2 500 m2。

另外，可以看到利用对最优模型求二阶导数的方法得到的面积(2 500 m2)比由实际种-面积曲线得到的面积(2 025 m2)要大475 m2，即理论曲线值(模拟曲线)与实际曲线值相比偏大，与王仁师等[3]的研究结果相似，该研究认为通过曲线求取最小面积时，理论曲线和实际曲线值结果均有偏差，前者偏大而后者偏小，应该在实际曲线值的基础上适当放宽边长，因此作为保守估测，应采用理论曲线得出的结果。根据该观点，二阶导数法得到的面积仅需要在实际种-面积曲线结果的每边长上增加5 m，就能得到更为全面准确的物种信息，因此最终确定桂林岩溶石山常绿落叶阔叶混交林最小面积为2 500 m2。

3 讨论

3.1 最优模型的选择

生物学模型要依据具体的研究目的和理论背景来选取[34]，因此选择种-面积曲线的拟合模型时不仅要从统计学的评价指标考虑，还应考虑具体的生物学意义。对8种曲线模型拟合效果分析发现，(7)洛莫利诺模型的AIC值低至25.337 3，这说明只考虑统计学指标时模型(7)是一个不错的选择，但该模型曲线的纵截距大于0，不符合“面积大于0才可能出现物种”的生物学实际，因此模型(7)排除。而模型(3)(4)(5)(8)都满足生物学意义的三点判断依据，但是从AIC值的拟合效果来看，模型(4)(5)(8)的AIC值均低于30，而(3)负指数模型的AIC值却高达54.367 4，即模型(3)虽满足三个条件，但拟合效果较差，可见对曲线的限制条件太多，有时会使拟合曲线的灵活性降低使拟合效果变差，与刘灿然[27]的观点一致，而(8)累积韦伯分布模型则既符合所有指出的条件，AIC值又最小，所以(8)为最优拟合模型。因此，应将赤池信息量准则(AIC值)与生物学意义综合起来评判模型的优劣，从两个方面充分考虑拟合优度，而不能只看其一。当然，研究中不一定二者同时满足，此时可结合实际调查情况，在拟合效果较好的模型中选取满足两个生物学意义条件的模型即可[31]。

3.2 群落总种数比例法与二阶导数法的比较

通过最优模型求取植物群落最小面积时，采取了群落总种数比例法和二阶导数法。采用群落总种数比例法时，由于比例因子ρ的取值不一样，所得到的最小面积也不同，王伯荪等指出在种类较为丰富且偶见种较多的群落中，很多偶见种对植物群落性质的影响并不重要[35]，唐龙等认为出于取样效率的考虑，应注意群落种类组成中的偶见种，仅需将含有样地总物种数84%的面积作为植物群落的最小面积[31]，因此比例因子ρ取0.84，此时由群落总种数比例法求得的最小面积为1 499 m2。采用后者，对最优模型的方程进行二次求导后作图，取S″值趋近于0的面积，求得的最小面积为2 500 m2。将两种方法分别求得的值与实际种-面积曲线进行比较，看到前者所求的植物群落最小面积偏低，因为群落总种数比例法是在种-面积曲线可以完全地、准确地反映该植物群落所有特征的前提下进行的，但由于尺度效应及区域分异的影响，直接通过区域尺度的种-面积关系来估计更大区域的物种多样性，将可能造成严重的低估，即群落总种数比例法求出的最小面积不足以体现桂林岩溶石山常绿落叶阔叶混交林的群落特征。相比之下，采用二阶导数法求取植物群落的最小面积更具科学性和准确性，与卓茜[28]、唐龙[31]等人的研究结果一致。

3.3 最小面积与经验值面积

植物群落组成越复杂，群落的最小面积就越大。目前，进行植物群落学调查常常通过经验值来确定取样面积。亚热带森林一般将取样面积定为400 m2，热带森林的则定为1 600 m2[36]。从研究结果来看，桂林岩溶石山区虽属于亚热带森林地区，但其植物群落的最小面积远不止400 m2，而是高达2 500 m2，两者所代表的物种多样性差距很大，可能是受桂林岩溶区独特的地形地貌影响。由于桂林岩溶石山地形破碎、岩石大多裸露出地表，地形因子异质性强导致土壤资源、水、光照等条件的分配呈现强烈的不均匀性，造成小生境类型的随机分布和不连续分布[37]，较强的生境异质性使该地区能维持较高的物种多样性[38]，通常而言，物种多样性高的地区所要求的群落最小面积也就越大，因而研究得到的桂林岩溶地区的最小面积远大于一般的亚热带森林，因此最小面积的确定应根据实际区域的物种特征来确定，若直接取该经验值来确定桂林岩溶石山植物群落调查的取样面积，将有可能导致对该地区植物物种多样性的严重低估，产生较大误差。

4 小结

采用随机样方法构建种-面积关系，通过999次随机抽样物种数取均值的方法得到桂林岩溶石山常绿落叶阔叶混交林的物种数随面积扩大而变化的数据规律，并据此绘制实际种-面积曲线，根据曲线的拐点初步判断最小面积为2 025 m2。

采用8种曲线模型对桂林岩溶石山常绿落叶阔叶混交林的种-面积关系进行拟合，综合赤池信息量准则(AIC值)和生物学意义来评价模型拟合优度，最终确定桂林岩溶石山常绿落叶阔叶混交林的最优拟合模型为：累积韦伯分布模型(cumulative Weibull)，拟合方程为：S=73.801 7(1-exp(-0.013 8A0.668 5))，且认为应将统计学评价指标(AIC值)与生物学意义综合起来评判模型的优劣，从两个方面充分考虑拟合优度，而不能只看其一。若研究中不能二者同时满足时，可结合实际的调查情况，在拟合效果较好的模型中选取满足两个生物学意义条件的模型即可。

利用最优模型求最小面积时，用群落总种数比例法对比二阶导数法，可见前者所求值偏低，而采用后者求取最小面积的方法更具科学性和准确性，最终确定桂林岩溶石山常绿落叶阔叶混交林的最小面积为2 500 m2。

目前进行群落学调查常通过经验值确定取样面积，但研究得出的桂林岩溶石山常绿落叶阔叶混交林最小面积与经验值存在较大差距，这可能与桂林岩溶地区独特的地形地质背景有关。较强的生境异质性使桂林岩溶地区能维持较高的物种多样性，所需要的群落最小面积也就远大于一般的亚热带森林。如果只通过经验来确定桂林岩溶石山植物群落调查的取样面积，有可能会低估该地区植物物种的多样性，说明最小面积的确定应根据实际区域的物种特征来确定。