套筒灌浆搭接接头拉伸试验及受力机理分析
2021-03-29王子沁白少华范宝秀董经民陈振海
余 琼,王子沁,白少华,范宝秀,张 志,董经民,陈振海,宫 鑫
(1.同济大学 结构防灾减灾工程系,上海 200092;2.山西建筑工程集团有限公司,太原 030006;3.山西二建集团有限公司,太原 030013)
套筒灌浆是比较成熟的预制装配混凝土结构钢筋连接技术之一,广泛应用于工程中,该连接采用套筒灌浆对接连接形式,套筒口径较小,一般比钢筋大25 mm左右,对施工精度要求高,当多根钢筋同时插入套筒时,施工难度较大。
套筒灌浆搭接连接是一种新型的钢筋连接型式,见图1,在两搭接钢筋外部放置套筒,注入灌浆料,实现钢筋的连接,这是笔者提出的钢筋连接专利技术[1]。该连接具有套筒直径较大,施工便利、灌浆易密实、造价低等优势。
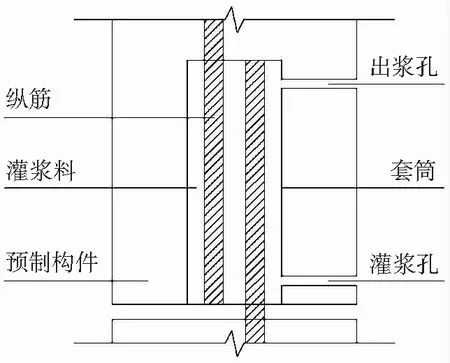
图1 套筒灌浆搭接Fig.1 Grouted sleeve lapping connector
该接头利用钢筋搭接传力,套筒约束两根钢筋及灌浆料,提高接头的承载力。近年来该接头的单向拉伸试验[2-3]和应用该接头的预制剪力墙[4]和框架柱[5]的拟静力试验研究表明,该接头受力合理,能有效传递钢筋应力,降低钢筋搭接长度,并且有着较好的延性性能。但该种接头的套筒应变尤其是纵向应变研究较少,受拉机理尚不明确。
本文进行36个钢筋套筒灌浆搭接接头的单向拉伸试验,以钢筋直径、搭接长度为研究参数,分析了套筒纵向、环向及套筒内、外钢筋应力应变曲线及试件的刚度、伸长比例和延性,得到了套筒纵向、环向应力分布规律以及钢筋的应变变化规律,分析了搭接接头的传力路径及受力机理,提出了接头极限黏结强度与临界搭接长度计算公式,为搭接接头设计提供理论依据。
1 试验概况
1.1 材性试验
灌浆料采用某公司的H-40灌浆料。根据GB/T 17671—1999《水泥胶砂强度检验方法》[6],测得40 mm×40 mm×160 mm的试件抗压强度为61.6 MPa,抗折强度为7.2 MPa;测得150 mm×150 mm×150 mm的试件劈裂抗拉强度为3.7 MPa。
钢筋采用强度等级HRB400,钢筋实测屈服强度见表1。
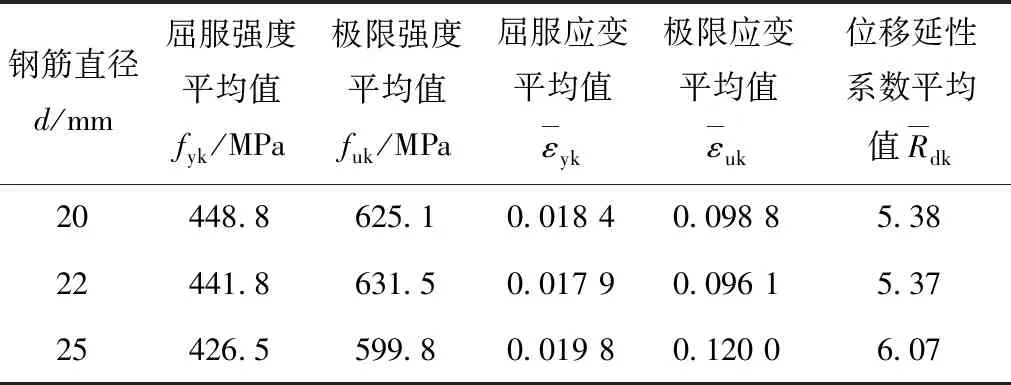
表1 钢筋材料性能Tab.1 Material properties of rebar
钢套筒采用Q235B热轧无缝钢管,屈服强度≥235 MPa,抗拉强度375~500 MPa,断后伸长率≥25%。
1.2 试件设计及量测内容
考虑施工中接头钢筋相对位置较不利的工况,试件预留钢筋在套筒两端进行点焊(固定钢筋位置),后插入钢筋紧贴预留钢筋并沿套筒直径方向放置(试验中,由于浇筑影响,两钢筋间略存在缝隙),套筒内灌入无收缩灌浆料。试验取接头处于最不利的情况(无侧向约束)进行,由于两钢筋搭接,套筒无侧向约束,在加载中试件发生图2所示的偏转,使套筒上下两钢筋有趋于共线的趋势。
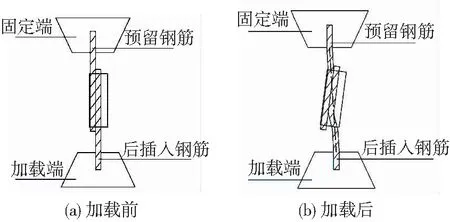
图2 加载后试件偏转情况Fig.2 Specimen deflection after loading
试件共有12组,套筒内径D为79 mm,套筒壁厚t为3.5 mm,改变钢筋直径d(分别为20、22、25 mm)及搭接长度L(分别为6d、8d、10d、12.5d)。试件示意见图3。
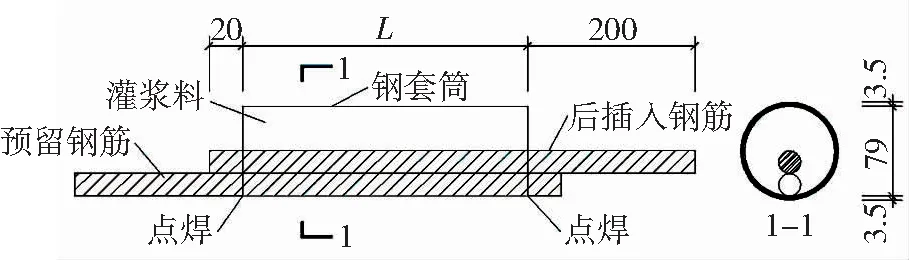
图3 试件示意(mm)Fig.3 Schematic diagram of specimen (mm)
沿预留、后插入钢筋纵向分别贴放应变片SG1~4,沿套筒纵向贴放应变片SG9~14(SG11~SG14仅用于钢筋直径d=25 mm的试件,SG9、SG10为1/2长度截面,SG11、SG12为1/3长度截面,SG13、SG14为1/6长度截面),沿套筒环向贴放应变片SG5~8。应变片具体位置见图4。
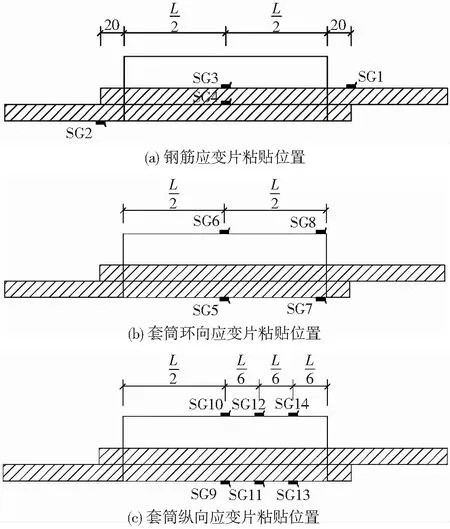
图4 应变片粘贴位置(mm)Fig.4 Layout of strain gauges (mm)
1.3 试验装置及加载方案
加载采用同济大学万能试验机,试验装置见图5。试验开始时以1 kN/s的应力速率加载至表2规定的荷载值(接近钢筋的屈服荷载),后以10 mm/min的分离速率加载,直至试件发生破坏。
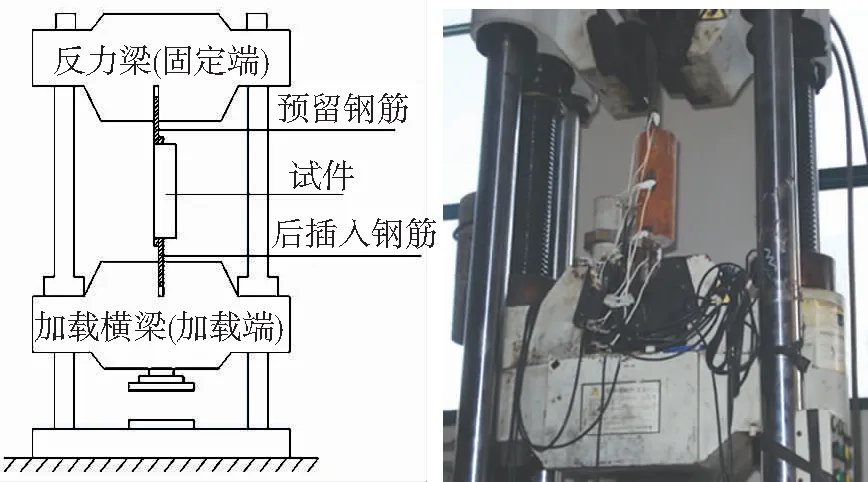
图5 试验装置示意Fig.5 Test setup

表2 加载速率变化时对应的荷载值Tab.2 Corresponding load when the loading rate changes
2 试验结果
2.1 破坏情况
试验取接头处于最不利的情况(无侧向约束)进行,试验结果表明试件有钢筋拉断和钢筋拔出两种破坏形式,见图6(a)、7(a)。

图6 试件钢筋拉断破坏Fig.6 Rebar tensile failure of specimen
对于搭接长度L=6d的试件均发生钢筋拔出破坏。达到试件极限强度时,钢筋尚未发生屈服,但钢筋从灌浆料中拔出,承载力迅速下降,发生滑移破坏。
对于L=8d和绝大多数L=10d的试件,同样也发生钢筋拔出破坏。但与L=6d的试件不同的是,在试件达到承载力极限状态前,钢筋达到屈服和强化阶段。
对于L=12.5d和少数L=10d的试件,破坏形态为套筒外部钢筋拉断破坏。灌浆料端部也出现局部破坏,但对试件承载力影响不大,其承载力主要取决于钢筋母材的力学性能。
固定端和加载端破坏情况有差异。试件固定端一侧破坏形态多为两钢筋搭缝间灌浆料开裂,见图7(a);试件加载端主要为钢筋与套筒间灌浆料局部挤压破碎,见图6(b)、7(b),灌浆料破坏比固定端严重。其原因见图8,试件固定端预留钢筋靠近套筒,套筒对其约束作用大;加载端后插入钢筋与套筒稍远,套筒对其约束小,因此加载端后插入钢筋变形大,其周围灌浆料也破坏严重。

图7 试件钢筋拔出破坏Fig.7 Rebar pullout failure of specimen
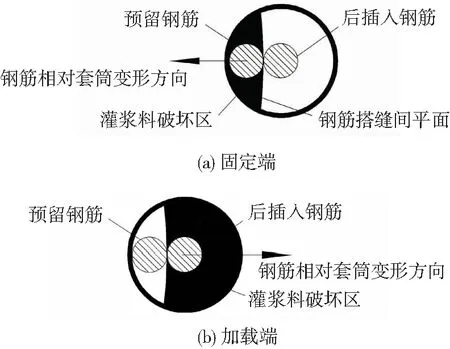
图8 试件两端局部变形情况Fig.8 Local deformation in both ends of specimen
2.2 承载能力
表3列出了各试件的破坏形态、屈服荷载Py、实测屈服强度fy、极限荷载Pu、极限抗拉强度fu、实测屈服强度与钢筋屈服强度标准值之比fy/fyk、极限抗拉强度与屈服强度比(强屈比)fu/fy。
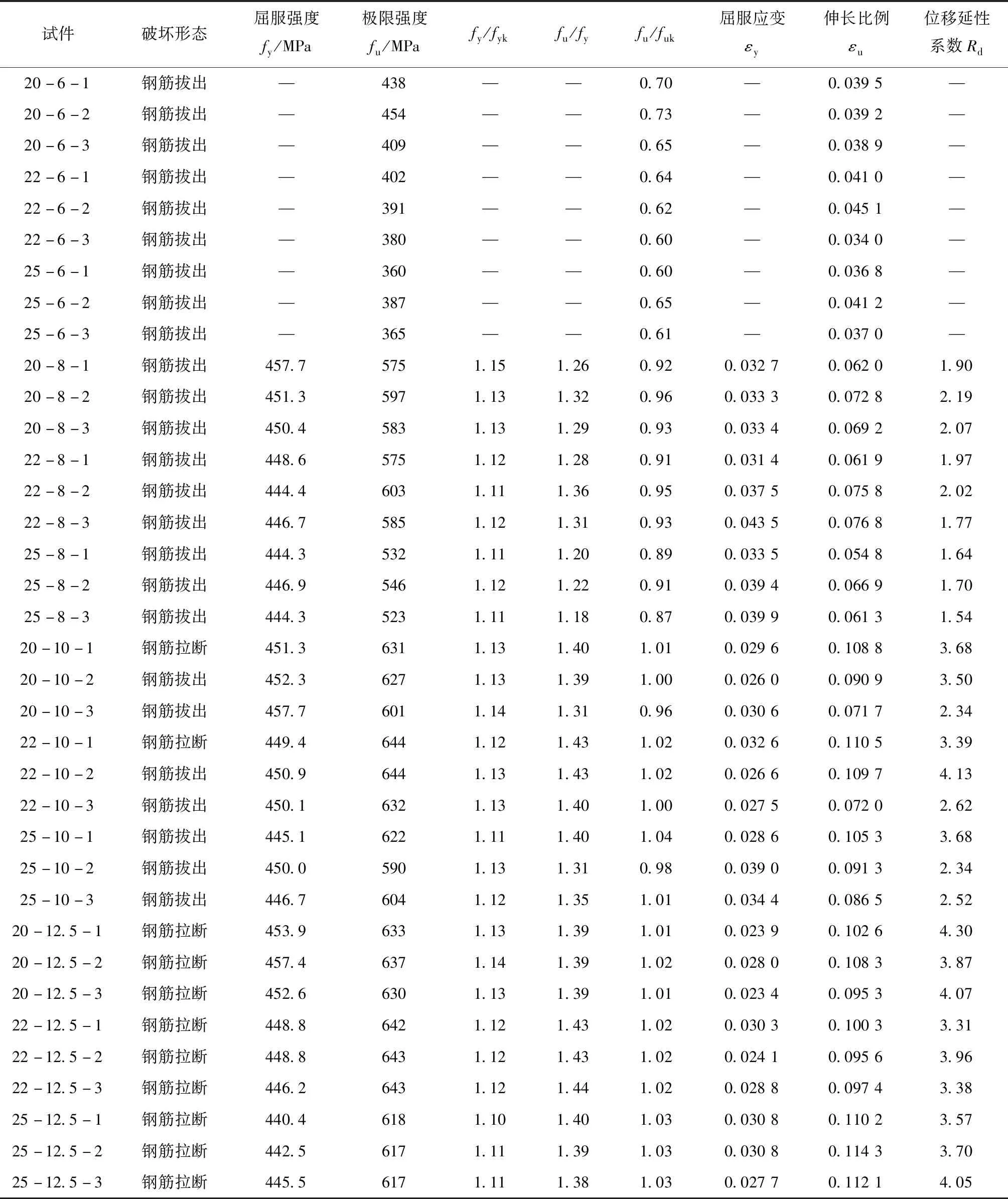
表3 试验结果Tab.3 Test results
JGJ 355—2015《钢筋套筒灌浆连接应用技术规程》[7]规定:接头的抗拉强度与连接钢筋的抗拉强度标准值比值fu/fuk大于1,且破坏时应断于接头外钢筋;接头屈服强度与连接钢筋屈服强度标准值比值fy/fyk大于1.GB 50011—2010《建筑抗震设计规范》[8]规定钢筋的抗拉强度实测值与钢筋屈服强度实测值的比值fu/fy不应小于1.25,钢筋屈服强度实测值与屈服强度标准值比fy/fyk不应大于1.3,本试验中套筒长度为12.5d的试件均满足以上要求。
图9为钢筋直径、搭接长度对试件极限承载力的影响。钢筋直径越大,试件极限承载能力越高,这主要是由于钢筋与灌浆料的接触面积和钢筋的强度随着钢筋直径增大而变大;而当钢筋直径不变时,发生滑移破坏时(搭接长度在10d及以下),随着搭接长度增加,试件的承载力增大。当发生钢筋拉断破坏时,试件承载基本相同。
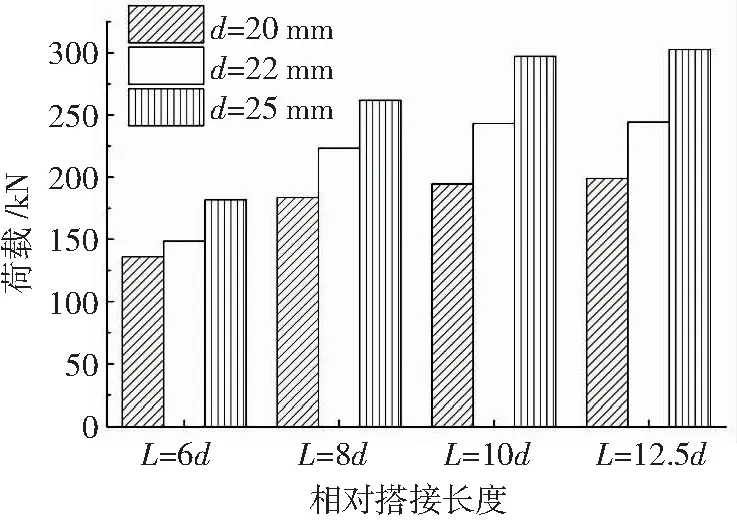
图9 钢筋直径、搭接长度对试件极限承载力的影响Fig.9 Effect of rebar diameter and lapping length on ultimate bear capacity of specimen
图10为钢筋直径、搭接长度对试件极限黏结应力的影响(L=12.5d的试件均为钢筋拉断破坏未列入其中),发现钢筋直径以及钢筋搭接长度对试件平均极限黏结强度影响不明显。
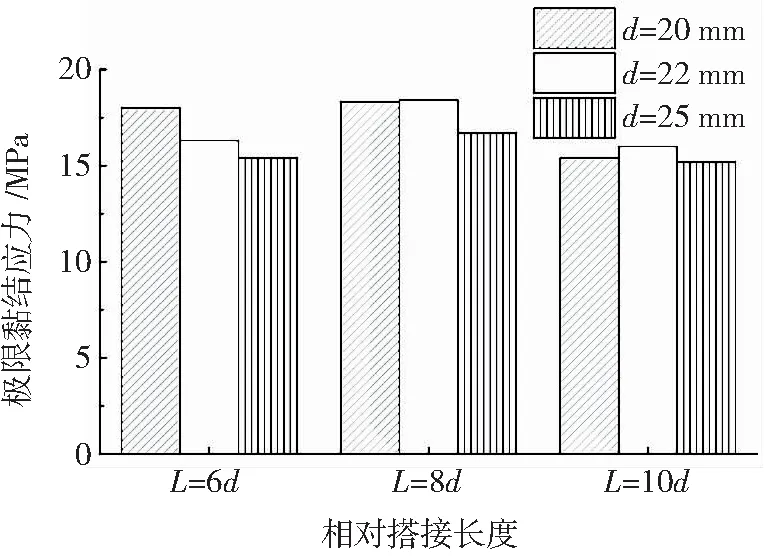
图10 钢筋直径、搭接长度对试件极限黏结应力的影响Fig.10 Effect of rebar diameter and lapping length on ultimate bond stress of specimen
2.3 试件荷载-平均应变曲线
图11(a)~(c)为试件具有代表性的荷载-平均应变曲线与钢筋材性试验曲线对比。其中平均应变为试验机加载点两端相对位移与加载点之间距离的比值。总的来说,搭接接头的荷载-平均应变曲线无明显的屈服台阶,主要是由于试验钢筋不在一条直线上、试件存在偏转引起。图11(d)为试件典型钢筋拔出、钢筋拉断的荷载-平均应变曲线与钢筋材性试验曲线对比,钢筋拉断试件与钢筋材性试验曲线基本吻合,钢筋性能利用充分;滑移试件达极限承载力时,由于锚固能力不足,钢筋与灌浆料间产生滑移,曲线进入迅速下降段(图11(d)中BC段),后进入平缓的下降段(图11(d)中CD段),此时为钢筋与灌浆料间摩擦力起作用。
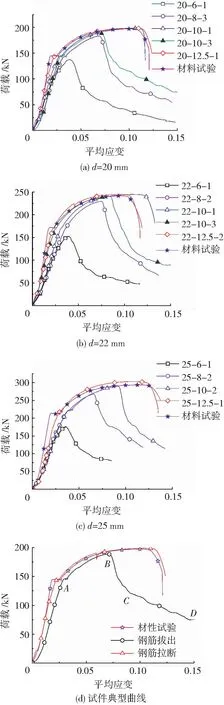
图11 荷载-平均应变曲线Fig.11 Load-mean stain curves
当钢筋直径相同时,搭接长度越大试件的初始刚度越大。这主要是由于荷载相同时,搭接长度较大的试件平均黏结应力较小,由钢筋肋间灌浆料的压缩变形和局部破碎导致的钢筋微量滑移引起的变形小。试件的刚度略小于钢筋的刚度,试件屈服应变大于钢筋的屈服应变,这主要是因为本试验接头存在偏转导致。
2.4 试件屈服应变、伸长比例及位移延性系数
表3中列出了试件的屈服应变、伸长率(极限应变)和位移延性系数,本试验中接头伸长比例是最大力下的两加载点之间的位移量与两加载点距离的比值,即极限荷载时接头的平均应变。位移延性系数Rd=δu/δy,其中δu是试件极限承载力对应的位移,δy是试件的屈服位移。
钢筋滑移试件的屈服应变是0.026 0~0.043 5,拉断试件的屈服应变是0.023 4~0.032 6。拉断试件的屈服应变大于钢筋材性试验的屈服应变(约为0.018 5),这主要是因为本试验接头存在偏转,导致两加载点间变形增加。
钢筋滑移试件的伸长比例是3.4%~10.97%,拉断试件的伸长比例是9.53%~11.43%。拉断试件的伸长比例与钢筋材性试验的伸长率相近,约为10%。
钢筋滑移试件的位移延性系数是1.54~4.13,拉断试件的位移延性系数是3.31~4.30。拉断试件的位移延性系数小于钢筋材性试验的位移延性系数(约为6)。
在拉伸过程中,套筒偏转会使套筒两端钢筋加载点间产生位移增量,加载达屈服时,试件屈服位移中该位移增量占比较大;而加载达到极限荷载时,由于钢筋伸长、滑移等因素,该位移增量占比变小,导致试件的位移延性系数略有降低。在实际结构中,由于套筒周围混凝土对接头偏转的约束,无该因素降低延性。同时根据孙佳秋[9]试验,增加有效防偏装置后,8d、10d、12d拉断试件的延性系数分别为3.81、3.66、4.33,可见偏转引起的延性降低很小,几乎可以忽略。
表4、5分别列出了试件的伸长比例和位移延性系数平均值。
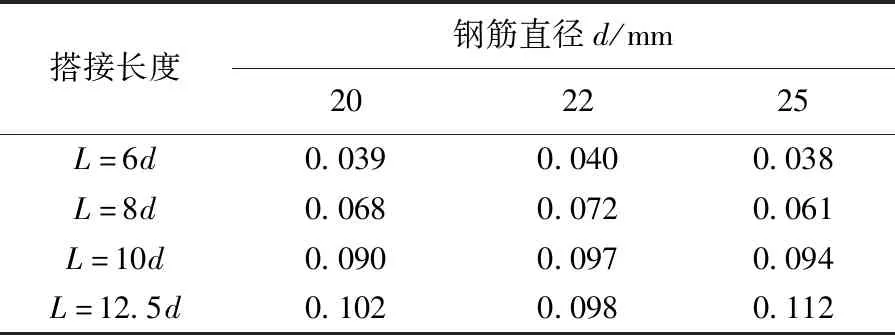
表4 试件最大力下的伸长比例Tab.4 Elongation of specimen under maximum force
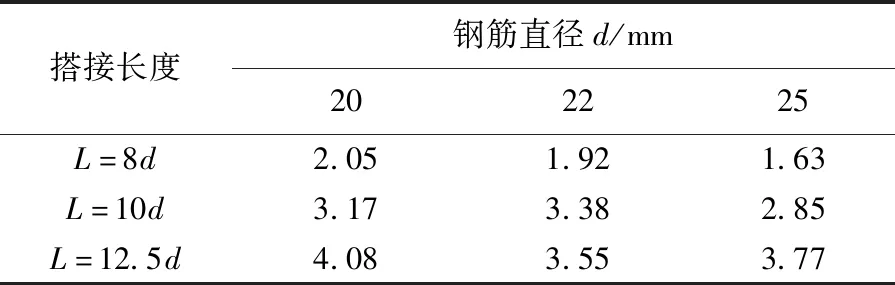
表5 试件位移延性系数Tab.5 Displacement ductility coefficient of specimen
从表4、5中可知,当钢筋直径相同时,L/d越大,试件的伸长比例及位移延性系数越大,表明试件的延性越好,这是由于锚固长度越长,试件承载力越大,试件破坏形态由钢筋拔出变为钢筋拉断,钢筋由未屈服达到屈服并向强化段发展,钢筋屈服应变、变形发展越充分,伸长比例以及位移延性系数越大。
美国规范ACI-318[10]及英国规范BS8110[11]中规定接头的位移延性系数Rd=δu/δy≥4。L/d=12.5时,试件延性系数基本接近4,基本满足规范要求。钢筋直径对试件的延性无明显影响规律。
3 试验应变分析
3.1 试验的套筒纵向应变
套筒的纵向应变也由两部分力引起,一是钢筋黏结力引起套筒的剪应力形成套筒的轴向力,前文分析的就是该力;二是灌浆料膨胀变形,使套筒环向受力,由于泊松比效应,引起的纵向受力,该力所占比例较小。
图12为套筒1/2长度截面近、远钢筋侧典型的纵向应变SG9、SG10的荷载-应变曲线。套筒1/2长度截面近、远钢筋侧套筒的纵向应变SG9、SG10在加载前期为拉应变,随着荷载的增大,逐渐转变为压应变。搭接长度越长,套筒纵向应变拉-压转变荷载逐渐增大,即套筒受拉状态持续越长。具体原因分析见4.2节。
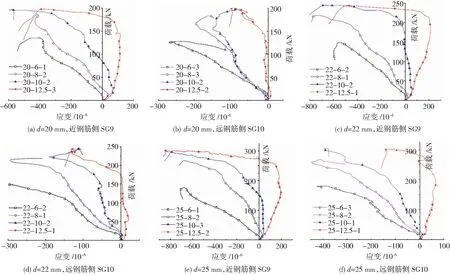
图12 套筒1/2长度截面典型的荷载-纵向应变曲线Fig.12 Typical load-longitudinal strain curves of middle section of sleeve
图13为相对搭接长度对套筒1/2长度截面所受的最大纵向拉应变影响图,套筒最大的纵向拉力发生在开始加载到拉压转变荷载间。近钢筋侧套筒纵向拉应变SG9随着搭接长度增大而增大,近钢筋侧筒纵向拉应变SG10该规律不充分。
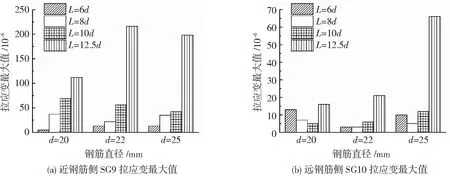
图13 相对搭接长度对套筒1/2长度截面最大拉应变的影响Fig.13 Effect of relative lapping length on the maximum tensile strain in middle section of sleeve
图14为相对搭接长度对极限荷载时套筒1/2长度截面近、远钢筋侧纵向压应变SG9、SG10极值的影响图,远钢筋侧套筒纵向压应变SG10随着搭接长度增大而变小,近钢筋侧筒纵向压应变SG9与相对搭接长度相关性不明显。
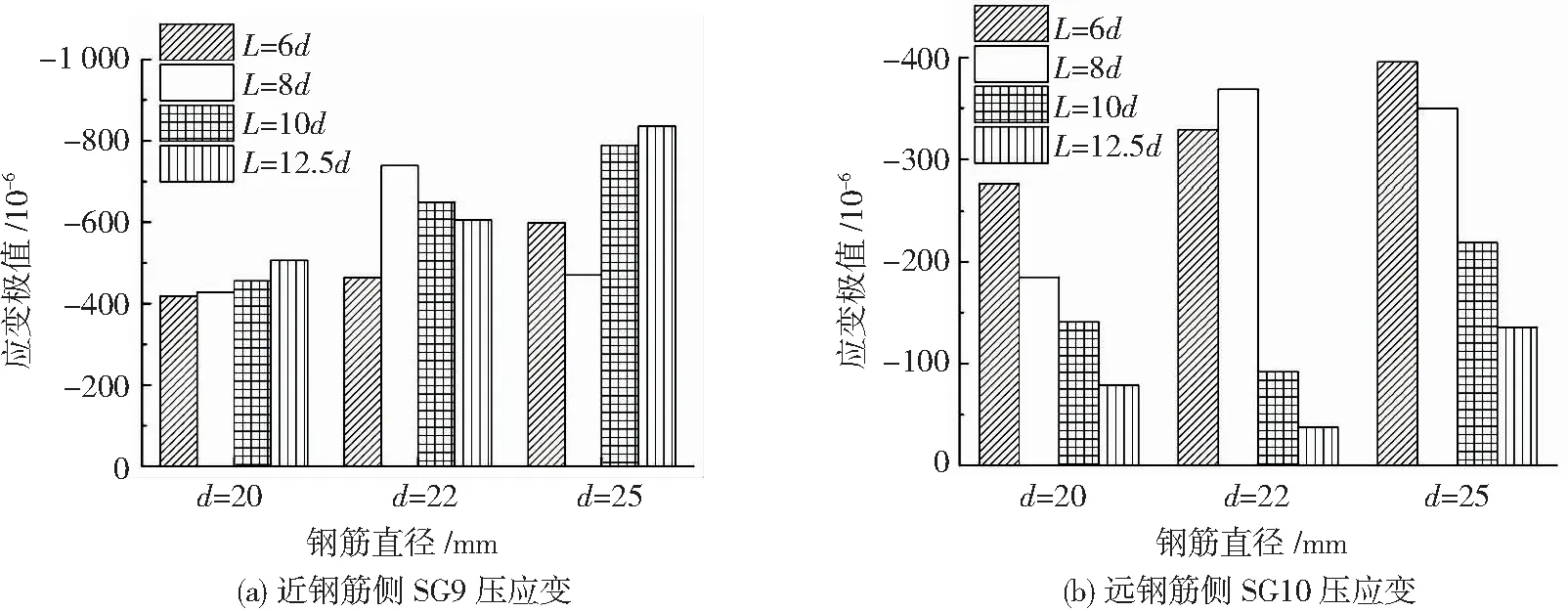
图14 相对搭接长度对极限荷载时套筒1/2长度截面纵向压应变极值的影响Fig.14 Effect of relative lapping length on the maximum longitudinal compressive strain in middle section of sleeve under ultimate load
随搭接长度的增大,套筒拉-压转化荷载增大,套筒受拉发展越充分,套筒拉力越大,拉应变越大,当搭接长度长时,一般为钢筋拉断破坏,试件受压阶段短,所以极限压应变也小,这是随搭接长度变化套筒中部纵向应变的发展一般规律。随着搭接长度增加,加载初期,近钢筋侧(SG9)套筒纵向拉应变大,该规律展现充分,而远钢筋侧拉应变小,该规律展现不充分;极限荷载时远钢筋侧(SG10)套筒纵向压应变变小,该规律展现充分,近钢筋侧(SG9)受偏转引起的压应变影响,该规律不明显。
图15为搭接长度12.5d时典型的套筒1/2、1/3、1/6长度截面的近、远钢筋侧的荷载-纵向应变曲线比较,在加载前期,近钢筋侧套筒所受到的拉力大于远钢筋侧套筒所受拉力(图15(c)中加载前期套筒1/6长度截面均受压,是由于试件偏转的影响);加载后期,近钢筋侧套筒纵向压力大于远钢筋侧纵向压力。说明整个加载过程中,套筒近钢筋侧的应变大于远钢筋侧。试验中,套筒纵向受拉时拉应变值小,纵向受压时压应力值略大,但未均超过钢材的屈服应变,表明钢套筒始终处于弹性工作状态。
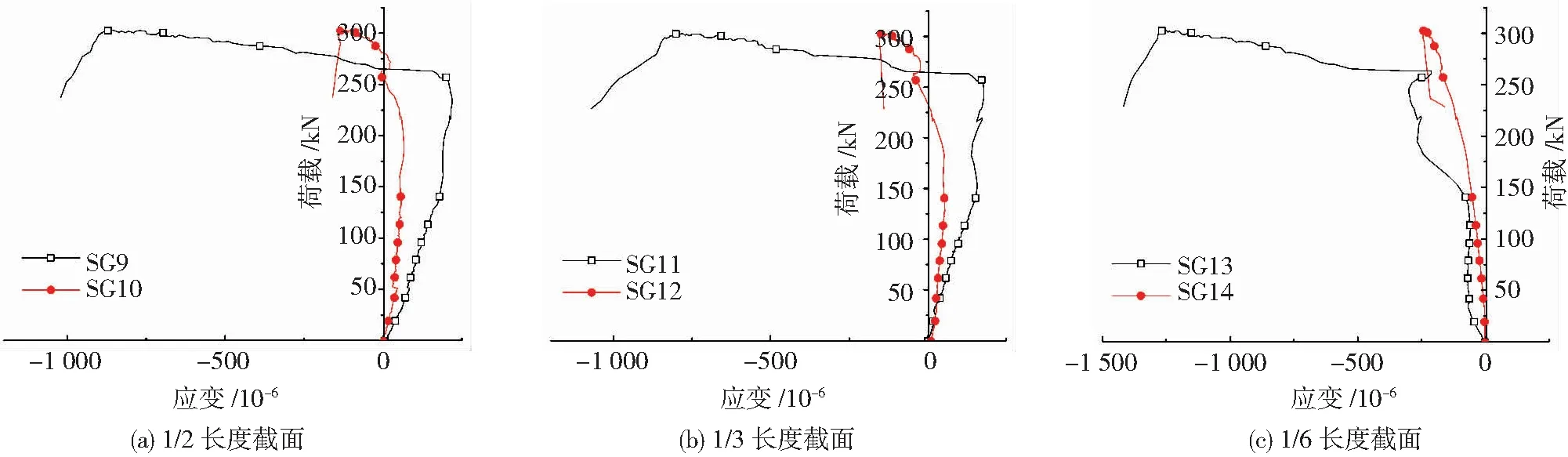
图15 25-12.5-1试件不同截面近、远钢筋侧套筒荷载-纵向应变曲线对比Fig.15 Comparison of load-longitudinal strain curves of specimen 25-12.5-1 in different sections of sleeve
3.2 试验套筒环向应变
3.2.1 套筒1/2长度截面
图16为套筒1/2长度截面近、远钢筋侧环向应变SG5、SG6的荷载-应变曲线。
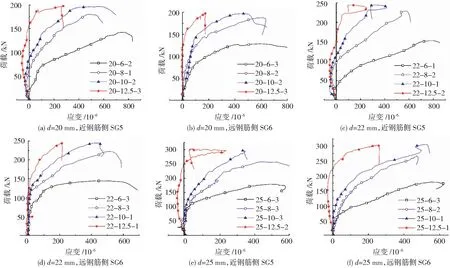
图16 套筒1/2长度截面荷载-环向应变曲线Fig.16 Load-circumferential strain curves of middle section of sleeve
套筒环向应变也由两部分力引起,一是灌浆料膨胀变形,使套筒环向受拉;二是钢筋黏结力引起套筒的剪应力形成套筒的轴向力,由于泊松比效应,套筒出现环向应力,该力所占比例较小。
在加载初期,套筒1/2长度截面近钢筋侧环向应变SG5主要由套筒的纵向应力控制。由于套筒整体纵向受拉,在泊松效应的影响下套筒径向收缩,表现为压应变;而在加载的过程中灌浆料膨胀逐渐起控制作用,套筒环向转变为拉应变。钢筋直径相同时,试件的搭接长度越大,套筒环向受压段越明显,压-拉转变荷载越大,这是由于搭接长度越大的试件平均黏结应力越小,其环向膨胀越小,环向压应变持续时间长,出现环向拉应变也越晚,压-拉转变荷载越大。
套筒1/2长度截面远钢筋侧的荷载-应变曲线随搭接长度变化的趋势与近钢筋侧相似,但直径为25 mm的钢筋近、远钢筋侧曲线相似程度最高(即锚固长度为12.5d直径为25 mm的钢筋加载前期环向有明显受压段,其余试件受压段不明显),这是由于钢筋直径越大,两搭接钢筋距离远钢筋侧越近,对其影响越大。
3.2.2 套筒边缘截面
图17为试件套筒边缘截面近、远钢筋侧环向应变SG7、SG8的荷载-应变曲线。在加载的整个过程中,套筒边缘截面环向应变均为拉应变。
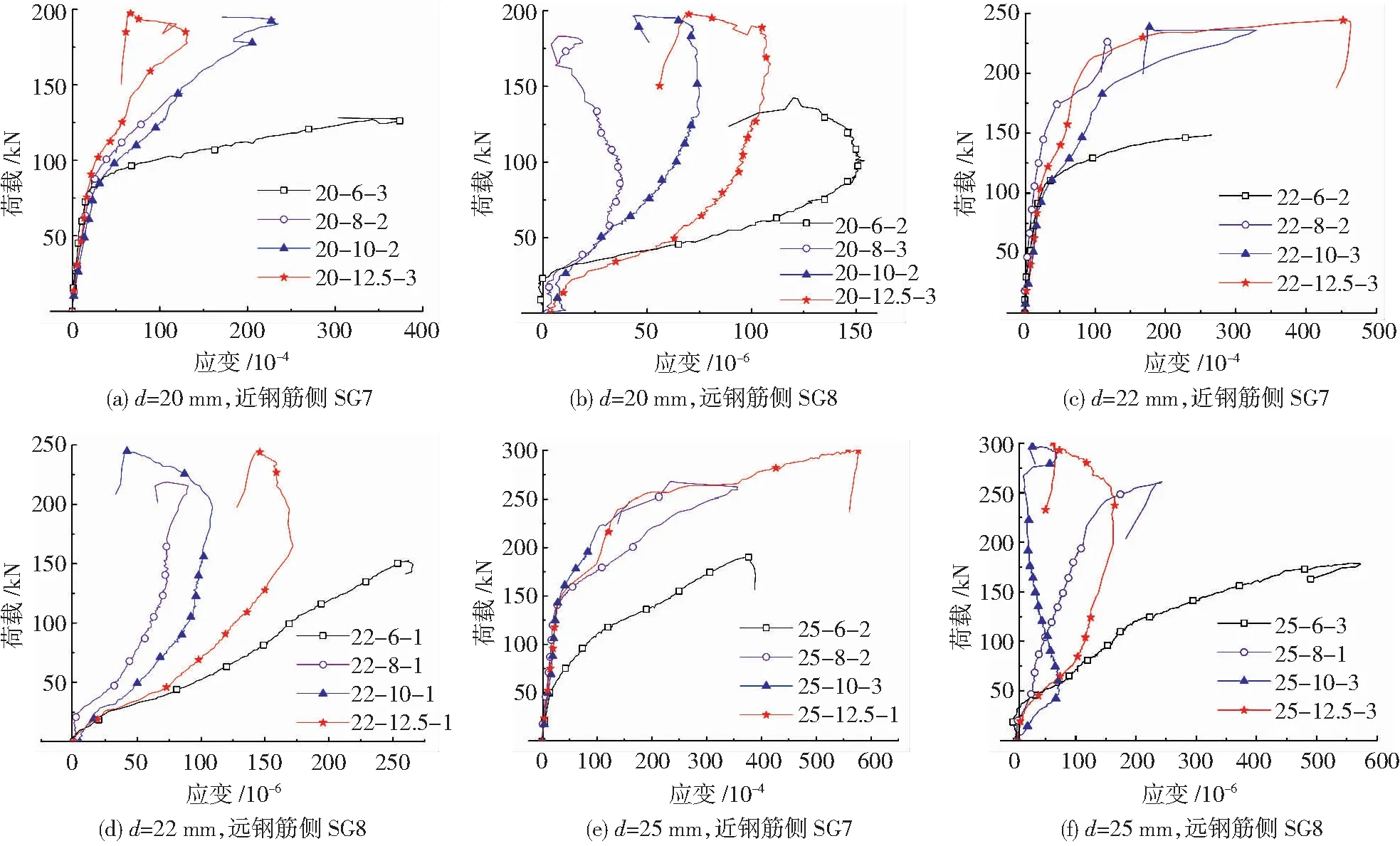
图17 套筒边缘截面荷载-环向应变曲线Fig.17 Load-circumferential strain curves of edge section of sleeve
对于近钢筋侧环向应变(SG7)达到钢材的屈服应变前,钢筋直径相同的荷载-应变曲线几乎重合,且基本为直线。套筒发生环向屈服后,试件荷载-应变曲线出现明显转折,套筒应变急剧增大,但由于这种环向屈服是发生在局部范围内的,因此试件的承载力仍保持继续增长。试件发生破坏时,套筒应变很大,部分试件应变片破坏。但由于其变形未超过套筒母材的实际极限拉应变,因此,未观察到套筒钢材断裂现象。
而远钢筋侧环向应变(SG8)均较小,未超过套筒母材的屈服强度,套筒处于弹性工作状态。
3.2.3 套筒远钢筋侧1/2长度截面(SG6)、端部截面(SG8)环向应变比较
图18为远钢筋侧套筒1/2长度截面(SG6)、端部截面(SG8)典型的荷载-应变曲线。总体上看,加载前期,边缘截面环向拉应变的发展速度比1/2长度截面快,同样荷载下边缘截面环向拉应变大于中部截面,但随着荷载的增加,边缘截面应变开始反方向发展,即荷载增加,套筒边缘截面环向应变降低,这说明边缘截面的灌浆料开始出现微裂缝及损伤,随荷载的增大远钢筋侧环向应变SG8应变进一步降低,最后SG8比SG6小得多。
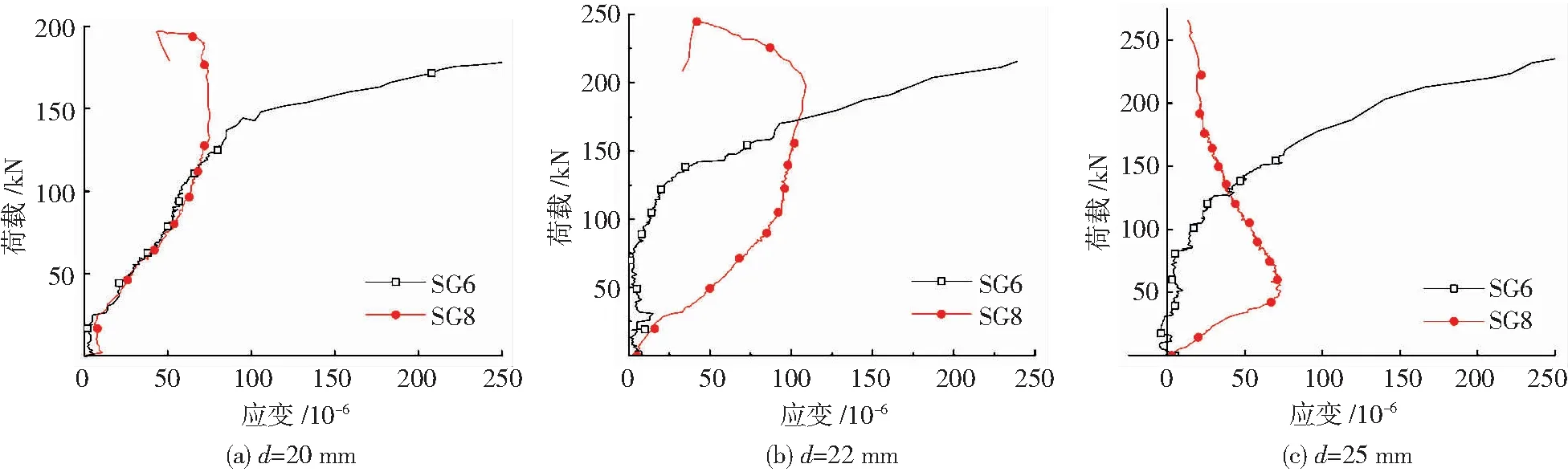
图18 SG6与SG8测点典型曲线(搭接长度10d试件)Fig.18 Typical curves at SG6 and SG8 (specimens with lapping length of 10d)
试件分别处于75 kN荷载与最大承载力时,套筒1/2长度截面与边缘截面远钢筋侧环向应变平均值比较见图19。在75 kN荷载下,试件远钢筋侧1/2长度截面环向应变SG6均小于边缘截面环向应变SG8。在极限荷载下,试件远钢筋侧1/2长度截面环向应变SG6比边缘截面环向应变SG8大得多。原因分析见4.2节。
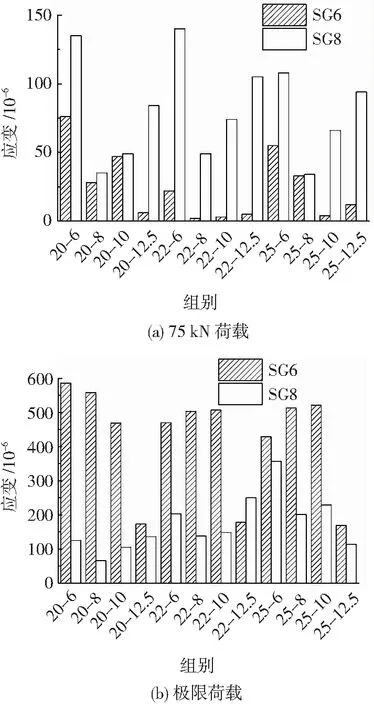
图19 75 kN荷载与极限荷载时SG6与SG8平均值比较Fig.19 Comparison of mean strain at SG6 and SG8 under 75 kN and ultimate load
3.3 钢筋纵向应变
图20为后插入钢筋(SG1)及预留钢筋(SG2)在套筒外部的典型的荷载-应变曲线(屈服前两者应变相差不大)。套筒外钢筋应变曲线表现出一定的屈服台阶,但与钢筋相比,屈服台阶偏短。
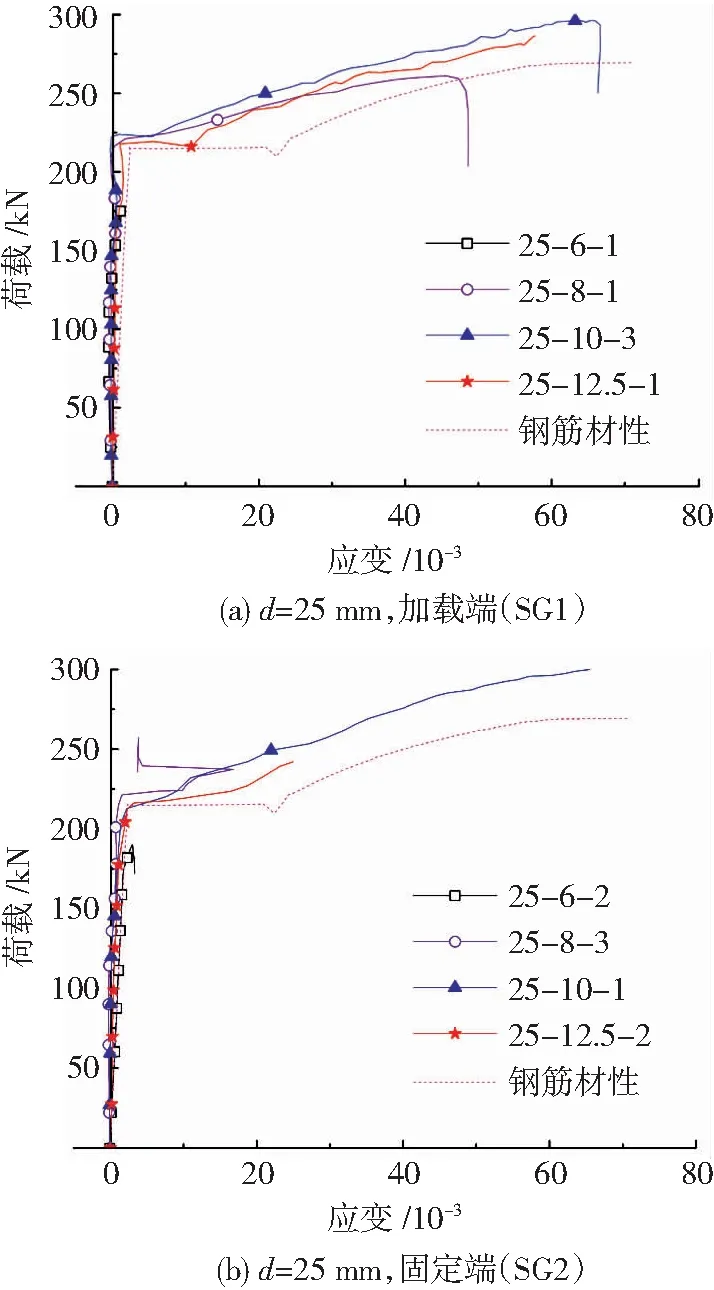
图20 套筒外典型钢筋荷载-应变曲线Fig.20 Typical load-strain curves of rebar outside sleeve
图21为套筒内部后插入、预留钢筋应变测点SG3、SG4的典型荷载-应变曲线。由于外部钢筋传给接头的荷载部分通过钢筋与灌浆料之间的相互作用传递,因此在同样荷载下,内部的应变小于钢筋材性试验的应变,由于钢筋材性试验屈服平台较长(2×103~2×104),图中钢筋材性曲线为部分曲线,并未表示出钢筋的强化段,故试件达极限承载力时钢筋还未进入强化段。
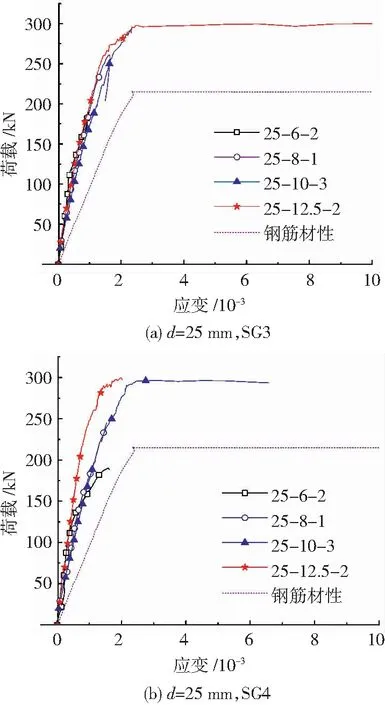
图21 套筒内1/2长度截面位置典型钢筋荷载-应变曲线Fig.21 Typical load-strain curves of rebar in middle section of sleeve
4 接头受拉工作机理及套筒黏结应力分析
4.1 接头受力机理
图22为钢筋套筒灌浆搭接接头传力路径示意图。传力路径有三种,通过两钢筋肋间灌浆料斜肢传力(当两钢筋贴近时,两钢筋贴近点处无该力,贴近点以外两钢筋间该力也较小,当两钢筋间有一定距离时,该力变大)、两钢筋间力通过钢筋外灌浆料直接传递以及两钢筋间力通过灌浆料-套筒-灌浆料传递。第一个传力途径占比较小。
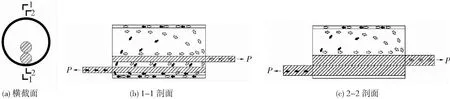
图22 钢筋套筒灌浆搭接接头传力路径示意Fig.22 Force transmission paths of grouted sleeve lapping connecter
而套筒灌对接接头处力路径只有两种:两钢筋间力通过灌浆料-套筒-灌浆料传递、两钢筋间力通过灌浆料直接传递,由于灌浆料抗拉强度有限,因此套筒传力占主导作用。
图23为套筒约束下两钢筋非贴近状态下肋间传力情况示意图。接头受拉时,两根钢筋受力方向相反,而两根钢筋都是带肋的,并且约束在套筒中,钢筋对灌浆料的作用见图23(a),有剪应力τ及斜压应力σ。肋间灌浆料斜肢受力情况见图23(b),σ又分解为τ′及σ′,σ′使钢筋周边灌浆料产生径向膨胀,见图23(c)。τ′为剪应力,使钢筋肋间灌浆料所产生的主拉应力σz使斜肢受拉,见图23(d),σz使斜肢出现撕裂裂缝如图23(e),灌浆料对钢筋反力σ′引起钢筋的分离趋势如图23(f)。
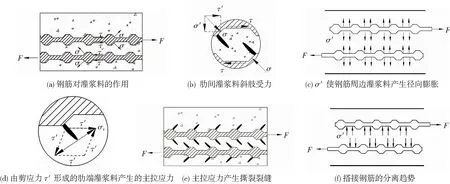
图23 套筒灌浆搭接接头钢筋传力情况Fig.23 Force transmission situations of grouted sleeve lapping connector
由于两根钢筋的对套筒的作用力方向相反,这样两钢筋对套筒作用的力大部分抵消,套筒所受的力小;而套筒约束的是两根钢筋的引起的灌浆料膨胀及两根钢筋的分离趋势,套筒对钢筋的约束大。
4.2 套筒内壁黏结应力分析
徐有邻[12]通过拔出试验测得长锚试件与短锚试件钢筋与混凝土之间的黏结应力沿锚固长度的分布随荷载的变化规律分别见图24(a)、24(b)。加载过程中黏结应力的发展,就是每一阶段沿钢筋纵向的最大的黏结应力由加载端向自由端变化的过程。
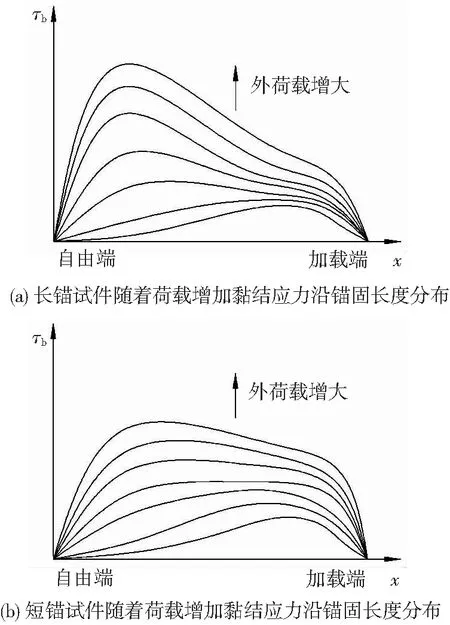
图24 钢筋-混凝土黏结应力沿锚固长度的分布Fig.24 Distribution of rebar-concrete bond stress along anchorage length
图25(a)为加载初期,在搭接长度范围内,两钢筋与灌浆料之间的黏结应力τb分布[13],而当加载至接近极限荷载时,τb分布见图27(a)。
在套筒纵向,套筒壁所受到的作用为两钢筋与灌浆料之间黏结力通过灌浆料传递至筒壁作用的叠加。由于两钢筋作用力方向相反,引起的灌浆料对套筒筒壁作用相反,相互抵消,套筒所受轴向力小。
影响套筒纵向力的因素有:1)钢筋-灌浆料黏结力的大小和方向;2)套筒上点与钢筋的距离,距离越近,套筒所受力越大。
两根钢筋的黏结应力沿长度方向是反对称的,在套筒1/2长度截面处,两根钢筋与灌浆料之间的黏结力大小相等,方向相反(图25(a)、27(a)中τ1等于τ2)。则在套筒1/2长度截面处的筒壁上,到两钢筋距离相等的点A、A′处受到的黏结力作用为0,图26为套筒1/2长度截面黏结力分布,图中“●”表示垂直平面向外,“×”表示垂直平面向里,符号的大小即表示黏结力的大小。套筒上B、C两点所受黏结应力方向相反。
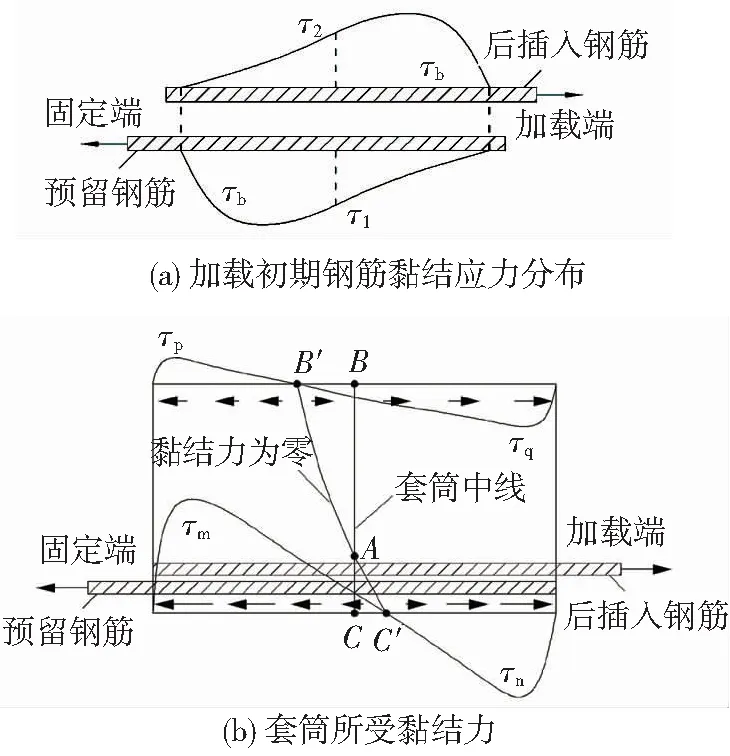
图25 加载初期套筒所受黏结应力分析Fig.25 Sleeve-grout bond stress at early stage of loading
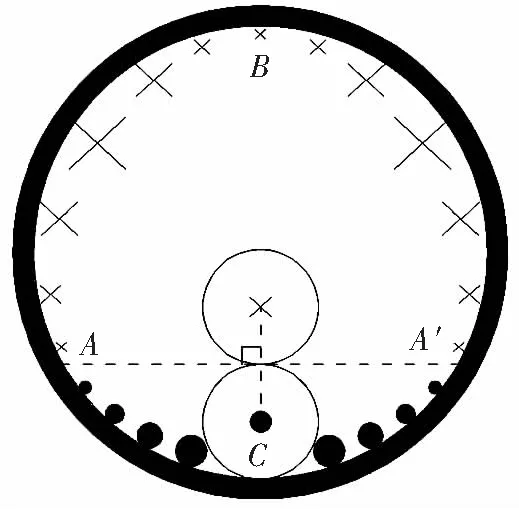
图26 1/2长度截面套筒与灌浆料间沿套筒纵向黏结应力分布示意Fig.26 Distribution of longitudinal sleeve-grout bond stress in middle section of sleeve
加载初期,由于钢筋与灌浆料之间的黏结力分布不均匀,图25(a)中,靠近两根钢筋受拉端的黏结应力较大,而靠近钢筋自由端位置,钢筋与灌浆料之间的黏结力几乎为0,因此对于套筒端部截面,套筒与灌浆料的黏结应力主要由受拉钢筋决定。
试件加载端,由于后插入钢筋所受的黏结力远大于预留钢筋所受的黏结力,因此该截面上套筒所受的黏结力大小及方向由后插入钢筋决定,套筒与后插入钢筋较近处黏结力较大,较远处则较小,试件加载端处的远、近钢筋侧套筒所受的黏结力与后插入钢筋受拉方向一致。
试件的固定端则与加载端相反,固定端截面上套筒所受黏结力主要由预留钢筋决定,固定端远、近钢筋侧套筒所受的黏结力与预留钢筋受拉方向一致。
在1/2长度截面处的远钢筋侧套筒上B点所受的黏结力与后插入钢筋受拉方向一致,在近钢筋侧C点与预留钢筋受拉方向一致;故试件套筒所受黏结力见图25(b),近钢筋侧黏结力为0的点C′偏向加载端一侧,远钢筋端黏结力为0的点B′偏向固定端一侧,可见套筒在加载初期灌浆料给套筒的黏结力方向相背离,套筒轴向受拉。试验中套筒1/2长度截面加载前期近钢筋及远钢筋侧纵向最大拉应变见表6,可见理论分析与试验结果吻合。从表中可以看出,套筒纵向最大拉应变为295×10-6,应变很小。
在加载到极限状态时,假设灌浆料无破坏情况,则钢筋与灌浆料之间的黏结力分布见图27(a)。与加载初期的分析类似,可以得到在极限荷载情况下时,在固定端处的远、近钢筋侧套筒所受的黏结力与后插入钢筋受拉方向一致;加载端处的远、近钢筋侧套筒所受的黏结力与预留钢筋受拉方向一致;由图26可知,在1/2长度截面处的远钢筋侧套筒所受的黏结力与后插入钢筋受拉方向一致,在近钢筋侧与预留钢筋受拉方向一致;图27(b)为按照上述分析所绘制的极限荷载时试件套筒所受黏结力情况,可见加载后期灌浆料给套筒的黏结力方向相对,套筒轴向受压。试验中套筒1/2长度截面极限荷载时近钢筋及远钢筋侧纵向压应变见表6,可见理论分析与试验结果吻合。钢筋拉断试件套筒纵向最大压应变为102.1×10-5,可见应变很小。
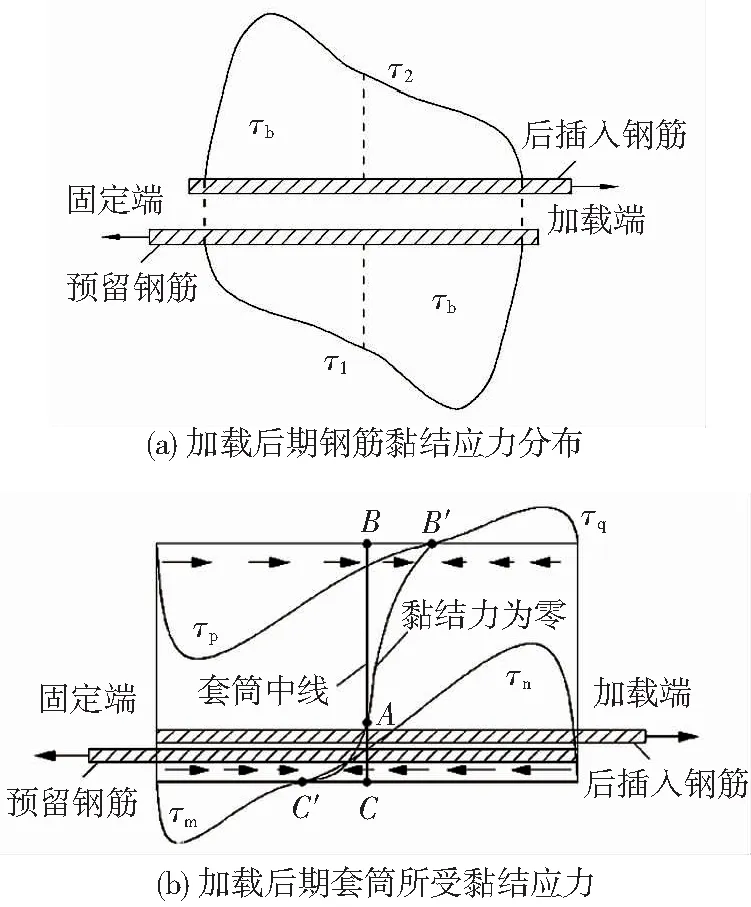
图27 极限荷载时套筒所受黏结应力分析Fig.27 Sleeve-grout bond stress under ultimate load
表6可看出,加载过程中套筒应变都很小,因此该接头对套筒材料性能要求低。加载前期近钢筋处的套筒纵向拉应变大于远钢筋处,极限荷载时近钢筋的纵向压应变大于远钢筋的压应变,即近钢筋上套筒的力大于远钢筋的,与机理分析中钢筋与套筒距离越近、套筒所受力越大观点吻合。

表6 试件1/2长度截面近钢筋侧及远钢筋侧套筒纵向应变情况Tab.6 Longitudinal sleeve strain near or away from rebar in middle section of specimen
根据受力机理,以下分析搭接长度越长,套筒纵向应变拉-压转变荷载逐渐增大的原因。钢筋在灌浆料中黏结应力变化过程即是钢筋表面最大黏结力由加载端向自由端发展的过程,见图24。搭接长度越长,钢筋起作用的黏结应力区段越长,最大黏结力向自由端的发展越慢,即由加载初期图25(a)状态转换为极限承载力图27(a)状态过程越慢,套筒纵向拉-压转变荷载越大。
根据受力机理,分析加载中边缘截面及中部截面环向应变变化情况。加载初期套筒边缘截面环向应变大于中部截面原因如下,表7列出了75 kN荷载下典型试件在套筒1/2长度截面的内部两根钢筋应变及合力情况,力F=AsEsεSG,As为钢筋截面面积,Es为钢筋弹性模量,取2.06×105MPa,εSG为钢筋在套筒中部截面应变。可以看出,套筒中部截面钢筋合力均小于外荷载75 kN,说明此时试件边缘截面一根钢筋受的力大于中部截面两钢筋的内力之和,根据受力机理图23(c),套筒的环向应变是由钢筋产生的径向膨胀力形成,因此边缘截面环向膨胀力大于中部截面,即SG8大于SG6。在极限荷载下套筒端部远钢筋侧的灌浆料脱落严重,套筒环向拉力迅速下降,故中部截面环向应变SG6大于SG8边缘截面环向应变。
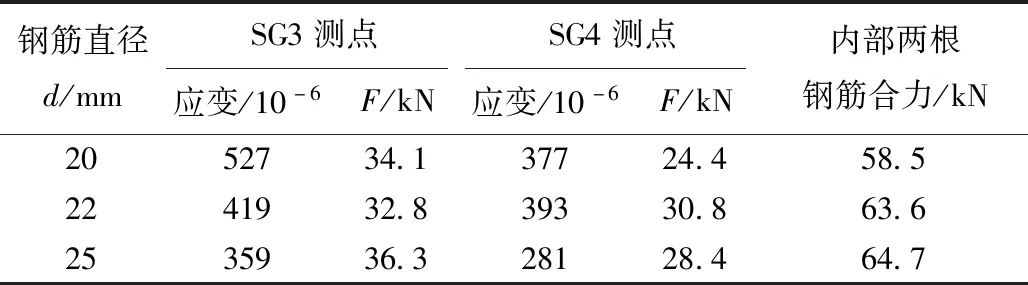
表7 75 kN荷载下套筒1/2长度截面内部钢筋合力Tab.7 Resultant force of internal rebar in middle section of sleeve under 75 kN
5 极限黏结强度与临界搭接长度计算
5.1 极限黏结强度
徐有邻等[14]进行了月牙纹钢筋的搭接对拉试验,指出影响钢筋搭接强度的因素有:砼强度、保护层厚度、配箍率和搭接长度,并根据试验数据的回归分析,得到钢筋搭接极限强度的计算公式:
(1)
式中:l为搭接长度,c为混凝土保护层厚度,ρsv为配箍率,ft为混凝土抗拉强度。
类似的,若将套筒视为配箍,分析本试验发生拔出破坏的试件可以得到,试件中钢筋黏结强度和以下因素正相关:灌浆料强度fts、配箍率ρsv、套筒相对厚度D/d、相对搭接长度的倒数d/L。其中套筒配箍率为
(2)
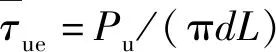
(3)
5.2 临界搭接长度
当钢筋与灌浆料间黏结滑移破坏与钢筋拉断现象同时发生时,此时的搭接长度为临界搭接长度,则有式(4)成立。其中fu取钢筋材性试验得到的钢筋极限抗拉强度,钢筋-灌浆料有效接触面积折减系数η取0.9。
(4)
由式(3)、(4)得到套筒灌浆搭接接头临界搭接长度的计算公式:
(5)
由式(5)计算得到的各组试件的临界搭接长度lcr和试验中试件发生破坏的临界搭接长度lcre的结果见表8,计算值与试验值基本一致,式(5)可用于套筒设计。
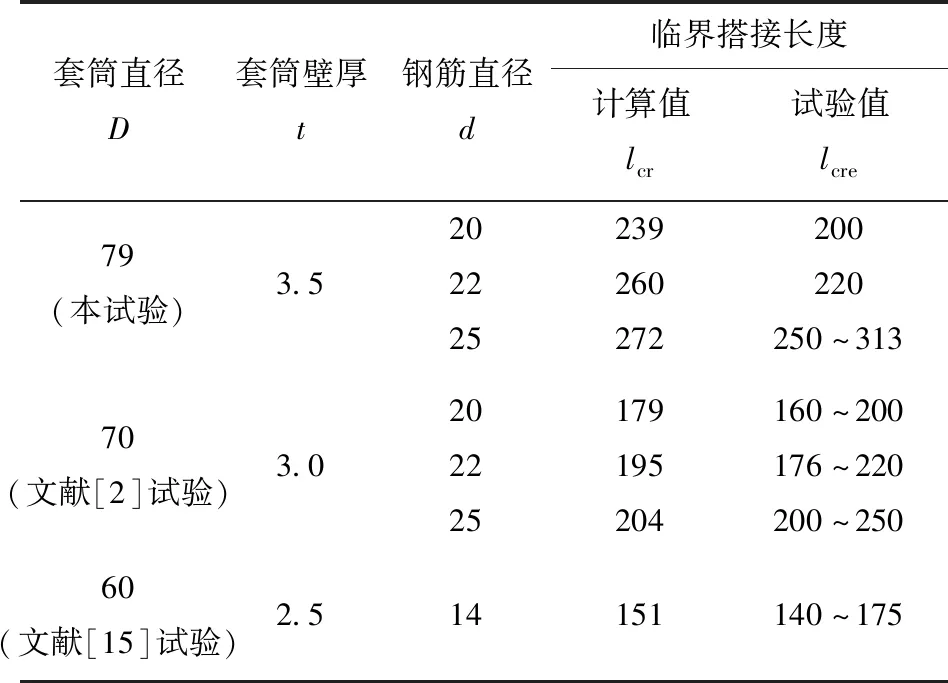
表8 试件临界搭接长度计算值与试验值对比Tab.8 Comparison between calculated and experimental values of critical lapping length mm
6 结 论
通过36个钢筋套筒灌浆搭接接头单向拉伸试验,得到主要结论如下,为按照本文构造方法浇筑的套筒灌浆接头的应用提供参考。
1)当相对搭接长度相同时,钢筋直径越大,钢筋与灌浆料的接触面积越大,试件的极限承载力越高。而当钢筋直径不变时,发生滑移破坏时(搭接长度在10d及以下),随着相对搭接长度增加,试件的承载力增大,当发生钢筋拉断破坏时,试件承载基本相同。
2)钢筋直径相同时,搭接长度越大试件的初始刚度越大(略小于钢筋母材的刚度),且试件最大力下的伸长比例以及位移延性系数越大。
3)试验中套筒1/2长度截面纵向应变在加载前期为拉应变,随着荷载的增大,逐渐转变为压应变。钢筋直径相同时,随着搭接长度的增大,套筒纵向拉-压转变荷载逐渐增大;加载过程中近钢筋侧套筒纵向拉应变随着搭接长度增大而增大,极限荷载时远钢筋侧套筒纵向压应变随着搭接长度增大而变小。
4)在加载初期,套筒1/2长度截面近钢筋侧环向受压,在加载后期环向逐渐转变为拉应变。试件的搭接长度越大,压-拉转变荷载越大;加载前期,套筒边缘环向应变值大于中部截面环向应变值;极限荷载时,端部灌浆料脱落,套筒中部环向应变值大于边缘截面环向应变值。
5)给出接头的传力路径,基于典型的钢筋-混凝土黏结应力分布曲线,分析套筒纵向应力分布及发展过程,得出加载初期套筒纵向受拉,加载后期套筒纵向受压,与试验结果吻合。试验结果表明套筒上近钢筋侧的纵向力大于远钢筋侧的,与机理分析中钢筋与套筒距离越近、套筒所受力越大观点吻合。
6)基于试验数据,拟合出了接头极限黏结强度公式,提出套筒临界搭接长度计算公式。