波函数法在成层半空间圆形隧道动力响应分析中的应用

马笑遇，袁宗浩，戴凯鑫，蔡袁强，罗 军，李旭东，孙宏磊

(1.杭州市地铁置业有限公司，浙江 杭州 310014；2.浙江工业大学 土木工程学院，浙江 杭州 310023；3.浙江万科南都房地产有限公司，浙江 杭州 310014)

目前，地铁列车引起的环境振动问题日益严重，公众对此类环境污染问题的敏感度日益提升。为了预测和评估环境振动对周边建筑物及居民的影响，学者们提出了许多分析模型对地铁列车运行引起的地基振动进行预测。Metrikine等[1]将隧道模拟为一根嵌入在黏弹性半平面内的欧拉梁，提出了一个较为简单的二维地下梁模型，用于研究欧拉梁上移动荷载引起的地面振动问题；Balendra等[2]提出了一个二维解析分析模型，用于研究平面应变条件下地铁列车荷载激励下的隧道-土体动力响应问题；在假设隧道直径远远小于土中波长的基础上，Krylov[3]将每一个枕木处传递的列车轴重作为埋置于三维半空间中点荷载，研究了地下列车运行引起半空间中波动传递特性。上述模型对地铁引起环境振动问题的模拟过于简化，有的将其考虑为二维问题，没有考虑波动在第3 个方向上的传播；有的未计入衬砌的几何尺寸，忽略了衬砌隧道的波导效应。后来，在圆柱形弹性理论的基础上，Forrest等[4-5]提出了一种“管中管”(Pipe-in-pipe, PIP)模型，内层管模拟中空的圆形衬砌隧道，外层管模拟衬砌周边土体，由于外层管考虑为全空间，该模型无法考虑地表反射作用对动力响应计算结果的影响；Hussein等[6]为了将“管中管”模型拓展至半空间中，提出了隧道位移不受地基表面影响的假设，并据此建立了半空间中圆形衬砌隧道动力响应的近似解析解；高广运等[7]基于Biot理论建立了2.5维地铁列车-隧道-饱和地基动力相互作用模型，研究了地铁荷载引起的饱和地基动力响应；Lu等[8]将圆形衬砌隧道分段处理，将衬砌管片视为弯曲梁，建立了考虑管片接头刚度弱化的隧道振动预测模型，数值结果表明管片接头处的刚度差对衬砌内力有较大影响；徐斌等[9]提出了移动荷载下层状饱和土地基的动力响应解析解，数值结果表明移动荷载作用下含有软弱夹层的层状地基比均质地基具有更大的动力响应水平。除了上述研究外，在地下隧道静和动力特性方面，蒲军平等[10]对公路隧道冲击响应问题，采用2D有限元进行了分析研究；王哲等[11]对浅埋暗挖隧道地面沉降槽宽度系数如何取值，开展了一系列数值模拟和试验研究；王克忠等[12]研究了渗流-应力耦合下，深埋引水隧洞变形的稳定性问题。

现有的研究成果尚缺乏移动荷载下成层半空间中圆形衬砌隧道动力响应的解析闭合解，为此，笔者提出一种适用于成层地基中浅埋隧道地基振动预测的解析模型，该方法可解决以往近似解析解[6]只适用于深埋隧道环境振动预测的问题，为地铁列车运行引起的地基振动计算提供新的预测手段。首先，将隧道模拟为中空圆柱体，将隧道周围土体模拟为具有圆柱形孔洞的(成层)半空间，带有圆柱形孔洞的半空间中总波场由外行的柱面波和下行的平面波构成，圆形衬砌隧道中的总波场由奇异的柱面波和非奇异的柱面波获得；其次，利用平面波和柱面波矢量波函数间的变换特性解决模型中直角坐标和柱坐标不匹配的问题；最后，通过数值算例研究荷载速度、荷载频率、土体阻尼比和土体成层性(地下水位变化)等因素对地表动力响应的影响。

1 控制方程与求解

半空间中圆形衬砌隧道模型示意图(x—y—z，三维)如图1所示。其中隧道模拟为中空圆柱体，隧道周围土体模拟为含有圆形孔洞的半空间，衬砌结构为黏弹性介质，周围土体为黏弹性介质或饱和弹性介质，土骨架材料参数为：密度ρ，Lamé常数λ和μ，衬砌结构材料参数为：密度ρ1，Lamé常数λ1和μ1。隧道内半径为a，外半径为b(衬砌厚度为h=b-a)，隧道中心距离地面距离为d。由图1可知：在隧道仰拱处施加荷载频率为f0，速度为c的单位竖向移动荷载。

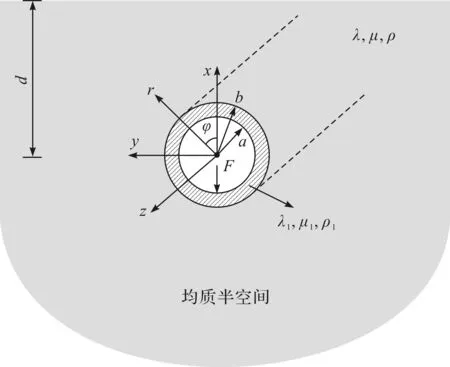
图1 均质半空间中圆形衬砌隧道模型示意图

在具有圆柱形孔洞的半空间中，波动的传播是一个涉及到两个散射面(地基表面、衬砌-土体界面)间多重散射作用的问题，含有圆形孔洞的半空间中总波场可以用外行的柱面波和下行的平面波之和表示，分别在直角坐标系和柱坐标系中描述平面波和柱面波，并通过施加地表和衬砌-土体界面上的边界条件获得含有圆形孔洞地基中的总波场。直角坐标系和柱坐标系间的不匹配问题可以利用不同波函数间转换性质得到解决。笔者首先给出平面波函数和柱面波函数以及二者之间的转换特性。

各向同性弹性体用位移表示的控制方程式为

(1)

式中u表示土体位移。

以ex为法向的平面上的应力矢量为

(2)

以er为法向的圆柱面上的应力矢量为

(3)

如图1所示，该问题是关于x—z平面的对称性问题，所以ux，uz，ur为关于y的偶函数；uy，uφ为y的奇函数。对于该对称性问题，平面坐标系下式(1)的完整解可表示为

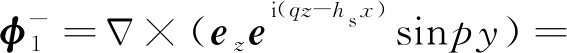
(4)

(5)

(6)

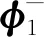
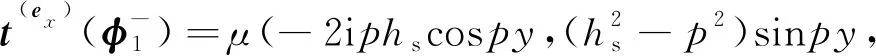
(7)

(8)

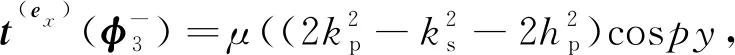
(9)

关于该对称性问题，式(1)在柱坐标系中的解可表示为Hankel函数、三角函数和指数函数的乘积，由此可定义外行柱面矢量波函数为

(10)

(11)

(12)

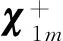
以er为法向的圆柱面上的应力分量为

(13)

(14)

(15)

带有圆柱形孔洞的半空间中总波场可表示为

(16)

为施加地基表面的边界条件(x=d)，需将外行的圆柱面波转换为上行的平面波，波形转换可通过Hankel函数的积分形式实现，即

(17)

(18)

式中sinαs,p=p/gs,p。

将式(17，18)代入式(10～12)，外行圆柱波将转换为上行平面波，可表示为

(19)

(20)

将式(19)代入式(16)中右端第二项，总位移场写为下行和上行平面波之和，可表示为

(21)

地基表面应力边界可表示为

(22)

通过求解包含3 个等式(x,y,z方向)的式(22)，未知数A1，A2，A3可表示为Bjm的函数，即

(23)

其中地表自由边界的反射系数Rjj为

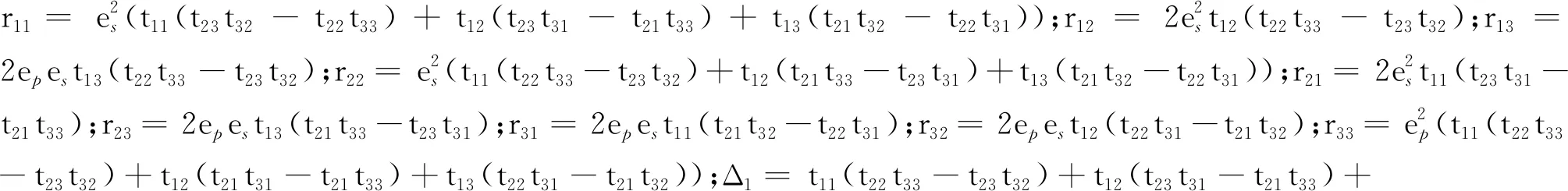
如何把村部的资源供给与村民的服务需求联结起来？笔者认为，关键在于管理者要改进村部管理方式，跳出把村部作为“固定资产”管理的惯性思维。不妨“敞开门”服务，从满足村民需求的角度开展工作，努力让村民有需求能想着村部、想办事能进得了村部、事不办结能依靠住村部。

同样，为了在隧道-土界面处施加边界条件，下行平面波应变换为奇异的圆柱波，从平面波到圆柱波的基本转换为

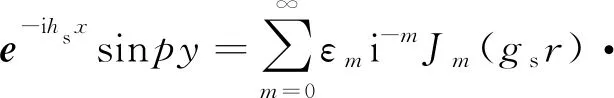
(24)

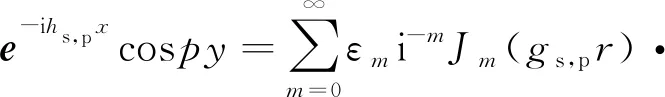
(25)

式中：εm为Neumann因子，ε0=1，当m≥1时，εm=2。

把式(24，25)代入式(4～6)，下行的平面波转换为奇异的圆柱波，可表示为

(26)

将式(26)代入式(16)右边的第一项，总位移场可以用外行波和奇异的圆柱波表示为

(27)

将式(23)代入式(27)，可消去未知变量Aj，总位移场可由未知变量Bjm在柱面坐标系中描述，即

(28)

其中Qjmj′m′(q)可以用数值积分得到

(29)

如图1所示，圆柱形衬砌隧道嵌入弹性半空间中，并在隧道仰拱处施加单位移动点载荷，衬砌结构内部位移场可表示为

(30)

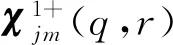
在隧道仰拱处(r=a,φ=π)施加单位移动点荷载，并用Dirac delta函数进行描述，荷载速度为c，频率为f0，函数式为

F=δ(φ-π)δ(z-ct)e-i2πf0ter

(31)

在频域中，F可以扩展为三角级数和关于q的傅里叶积分为

(32)

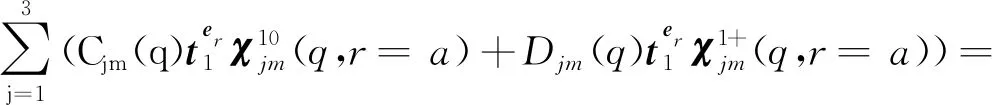
(33)

式中：对于每个m可推导出3 个等式(r，φ，z分量)，从而Cjm可以用Djm来表示(j=1, 2, 3)。

根据式(29，30)可得到隧道-土界面处(r=b)的位移连续条件为

(34)

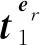
(35)

式(33～35)为计算未知变量Bjm(q)，Cjm(q)，Djm(q)的3 组方程，任一组方程中对于每一个m均有3 个等式(r，φ和z分量)，可给出了一个与未知数个数完全相同的线性方程组，从而完成求解。由式(23)可知未知常数Aj(q,p)可以由Bjm(q)得到。至此，所有的系数(Aj(q,p)，Bjm(q)，Cjm(q)，Djm(q))都可通过相同数目的线性方程完成求解。最后，把Aj(q,p)，Bjm(q)代入式(23)可获得隧道周围土体的位移场，同样把Cjm(q)，Djm(q))代入式(30)可得到衬砌隧道内的位移场，时域中的数值结果可以通过关于ω的Fourier逆变换得到。

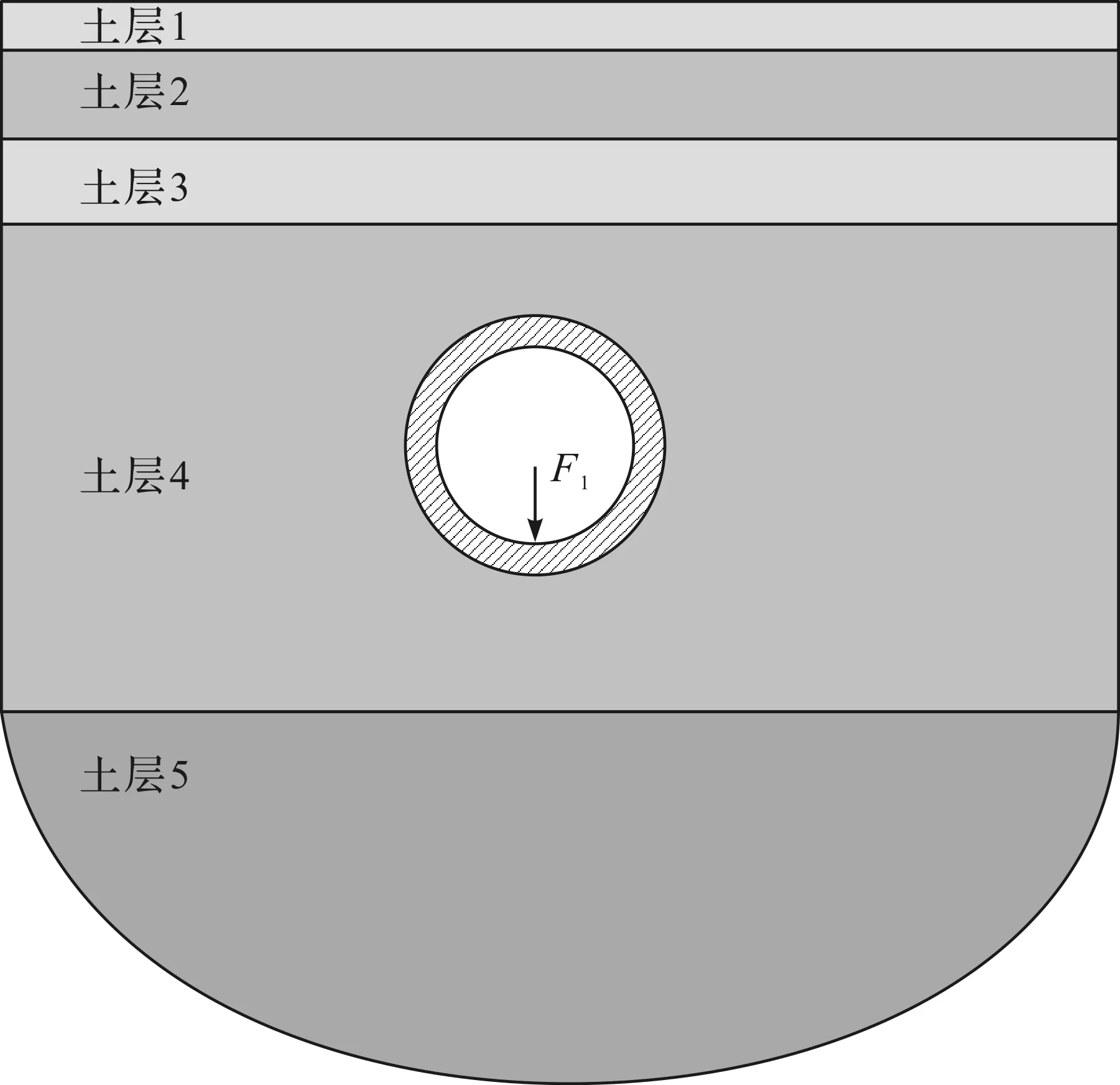
图2 成层半空间中圆形衬砌隧道模型示意图

2 数值结果与讨论

2.1 模型验证

为验证笔者提出解法的正确性，本节与文献[6]中的近似解析法计算结果进行对比，选取文献[6]中的工况5作为对比的参照。文献[6]中的成层半空间由5 层地基土组成(图2)，5 层地基土层厚由上至下分别为1，3，1，20 m和∞(下卧半空间)，5 层地基土的弹性参数如表1所示，圆形衬砌隧道埋置在第4 层土中，隧道中心距离地表(埋深)为d=20 m，隧道衬砌为混凝土材料，杨氏模量E1=50 GPa、泊松比ν1=0.3、密度ρ1=2 500 kg/m3、阻尼系数为0.03。

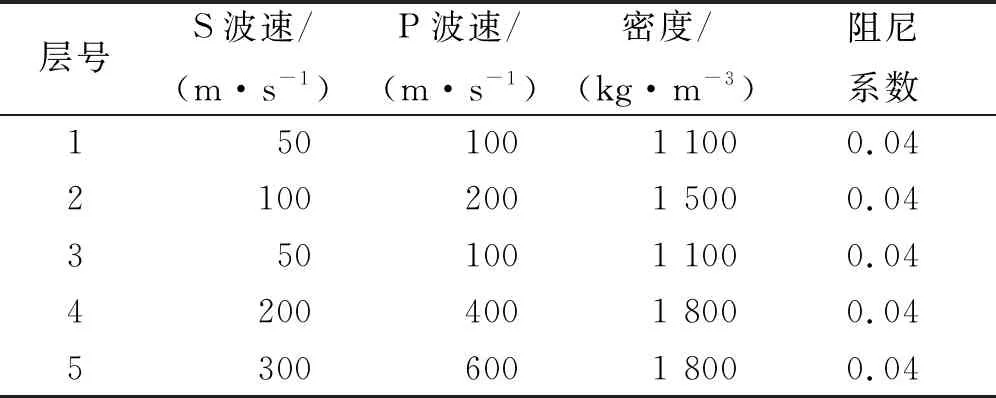
表1 成层地基的土体参数

图3给出了在衬砌仰拱处作用单位简谐点荷载(c=0，f=1～80 Hz)，地表观察点(坐标为x=20 m，y=0，z=0)的竖向位移响应。由图3可知：当隧道埋深较大时，笔者提出的解法与文献[6]中给出的近似解析解结果吻合较好，进而验证了笔者解法的正确性。应指出，文献[6]提出的近似解析法只适用于隧道埋深大于2倍的隧道直径的情形，对于浅埋隧道近似解析法与真实解间存在较大误差，而笔者解法考虑了地表与隧道间的多重散射作用，对深、浅埋隧道均适用。

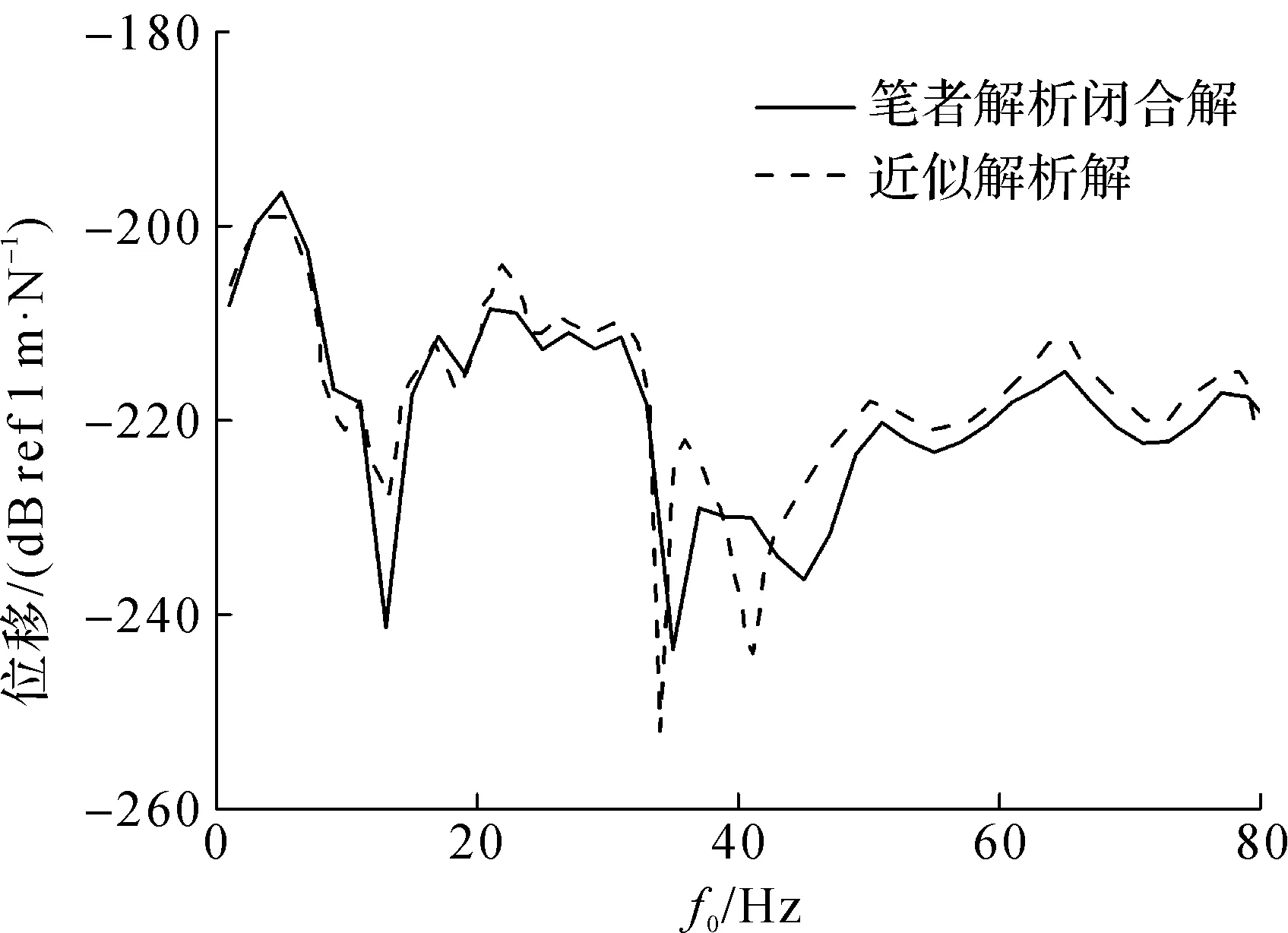
图3 笔者计算结果与文献[6]计算结果对比

2.2 荷载速度的影响

本节将通过数值算例说明笔者解法用于成层地基波动特性分析的适用性，首先建立如图1所示的均质半空间模型，研究荷载移动速度对地表振动响应的影响(f0=0)，隧道中心至地表的距离选取为d=5 m，隧道外径b=3 m、内径a=2.75 m，衬砌的杨氏模量E1=50 GPa、泊松比ν1=0.3、密度ρ1=2 500 kg/m3、阻尼系数0.03。同时，均质半空间选取为软土地基参数：横波波速cs=100 m/s、纵波波速cp=200 m/s、密度ρ=1 500 kg/m3、阻尼系数为0.04。在隧道仰拱处垂直施加一个单位力(1 N)，并以速度c沿隧道延伸方向移动，荷载频率为f0。为展示计算结果，选择两个地表观察点，A点的坐标为(5 m, 10 m, 0)(隧道左侧地表)，B点坐标为(5 m, 0, 0 )(隧道中轴线正上方)。

图4给出了不同荷载速度c(f0=0)下地表观察点A在单位移动点荷载作用下的最大位移和最大速度响应，计算了竖向(x)、水平(y)和轴向(z)等3 个方向的响应分量。由图4可知：当荷载移动速度接近地基土的剪切波速时，竖向和轴向的位移、速度响应达到峰值，体系发生共振；对于横向动力响应，当荷载移动速度小于剪切波速时，响应缓慢增加，一旦荷载速度超过剪切波速，荷载动力响应迅速增大。上述现象可解释为：剪切波速作为孔洞表面的面波波速，当荷载移动速度达到该面波波速时，体系内会激发衰减较弱的行进波传播，体系发生共振，进而动力响应显著增大。

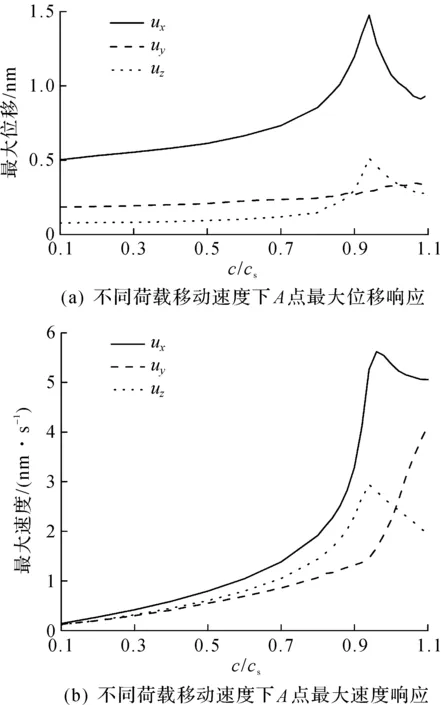
图4 地表A点的最大位移和最大速度响应

图5给出了不同荷载速度下(f0=0)地表位移和速度响应沿空间(横向)的衰减情况。选取了4 个速度工况，荷载移动速度c分别为30，60，95，110 m/s。当荷载移动速度c=95 m/s时，荷载速度最为接近面波速度(地基剪切波速100 m/s)。由图5可知：此时地表显示出了最大的振动响应，且当荷载移动速度在剪切波速附近时(c分别为95，110 m/s)，地基动力响应的空间衰减率显著降低，速度响应衰减率则更明显。

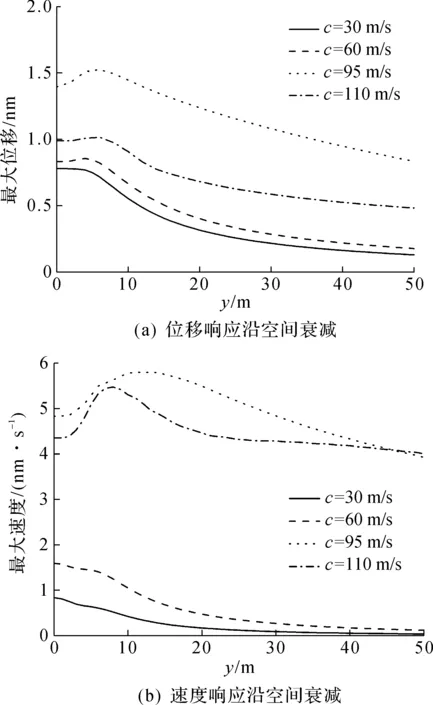
图5 不同荷载速度下地表响应沿空间衰减

2.3 地基成层的影响

如前所述，笔者提出的解法适用于成层地基，可以分别在隧道上方和下方添加解析土层单元，获得多层成层地基中圆形衬砌隧道解析模型(图2)。通常成层地基土体为上软下硬或上硬下软结构，为研究地基成层特性对地表振动特性的影响，采用如图6所示的两层土半空间模型用于分析地基土成层特性。隧道埋深d=5 m，上覆土层厚度d-d1=2 m，下卧半空间和衬砌材料参数同2.2节，上覆土层刚度参数以下卧半空间刚度参数为基准分别减小50%和放大50%，用以描述上软下硬(工况1)和上硬下软(工况3)成层地基，并将两土层刚度参数一致构成的均质半空间作为参考工况(工况2)。上覆较软土层具有剪切波速cs2=70.7 m/s和纵波波速cp2=141.4 m/s，上覆较硬土层具有剪切波速cs2=122.5 m/s和纵波波速cp2=245 m/s，上覆土层的密度和阻尼比与下卧半空间相同。

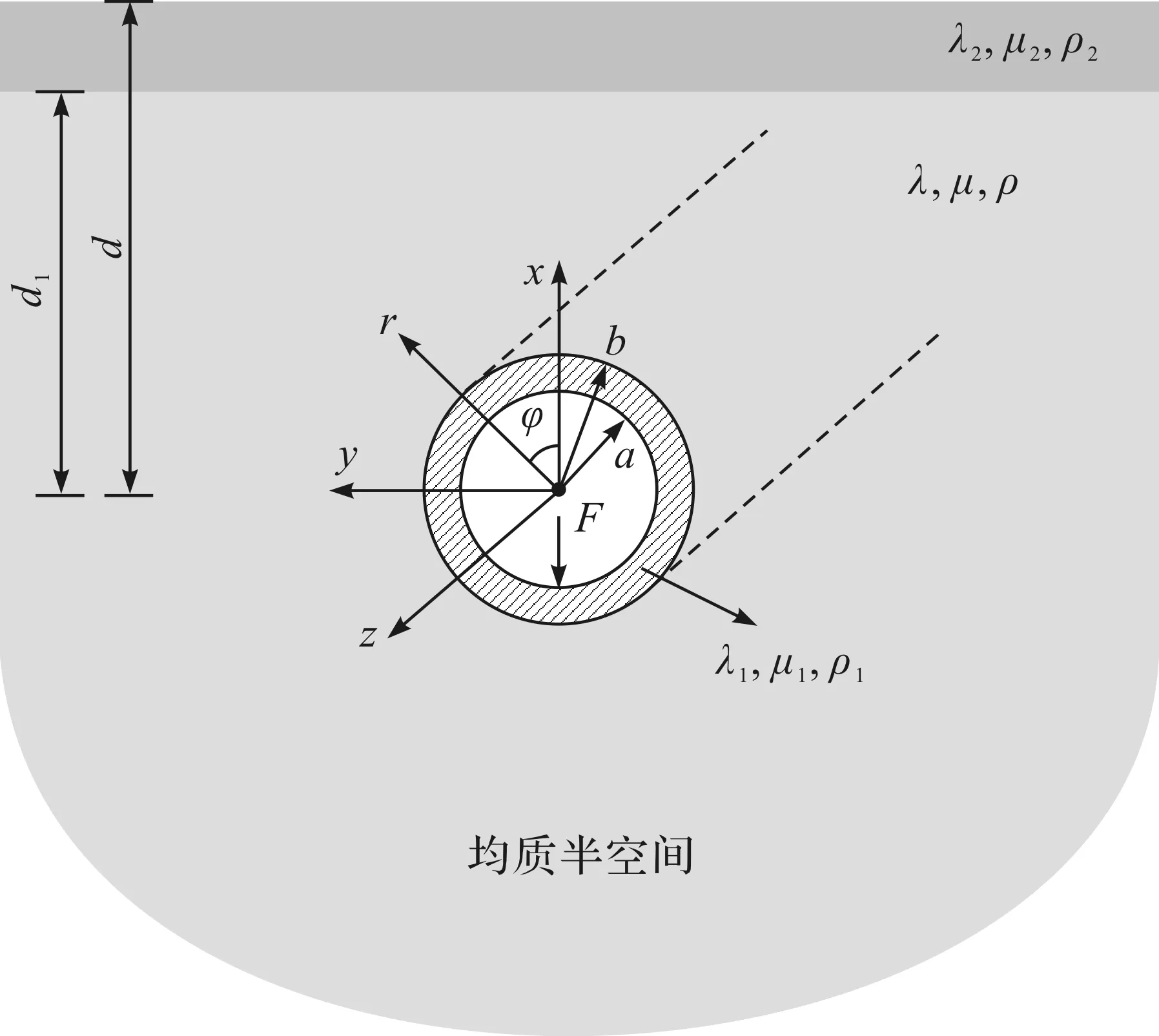
图6 成层地基中圆形衬砌隧道模型示意图

3 种工况下地表A点和B点位移响应的比较如图7所示。其中工况1为上覆较软土层，工况2为均质土层，工况3为上覆较硬土层。由图7可知：在低频范围内，上述3种工况之间的差别较小，这是因为此时波长较大，振动波并未明显地感知到地基土的成层特性；随着荷载频率的增大，3 种工况间的差异逐渐增大，最大差异幅值可达20 dB；正如预期的那样，在总体规律上，上覆软土层(工况1)由于地基刚度较小，地表振动响应最大，反之，上覆硬土层(工况3)给出了最小的位移响应。通过图7各子图的对比还可以发现，地基上覆土层刚度变化对竖向位移的影响大于对水平位移的影响。

图7 上覆较软和较硬土层对A，B点位移的影响

2.4 地下水位的影响

上述2.2和2.3节中地基土考虑为单相介质，并未计入孔隙流体的存在对地基振动的影响，笔者提出的解法可以通过引入P2波和水力边界条件，建立饱和成层地基中圆形衬砌隧道模型，进而分析水相参数、地下水位变化等因素对地表波动传播的影响。地下水位的变化可通过改变上覆干土层厚度实现，下卧半空间为饱和两相介质，如图8所示。

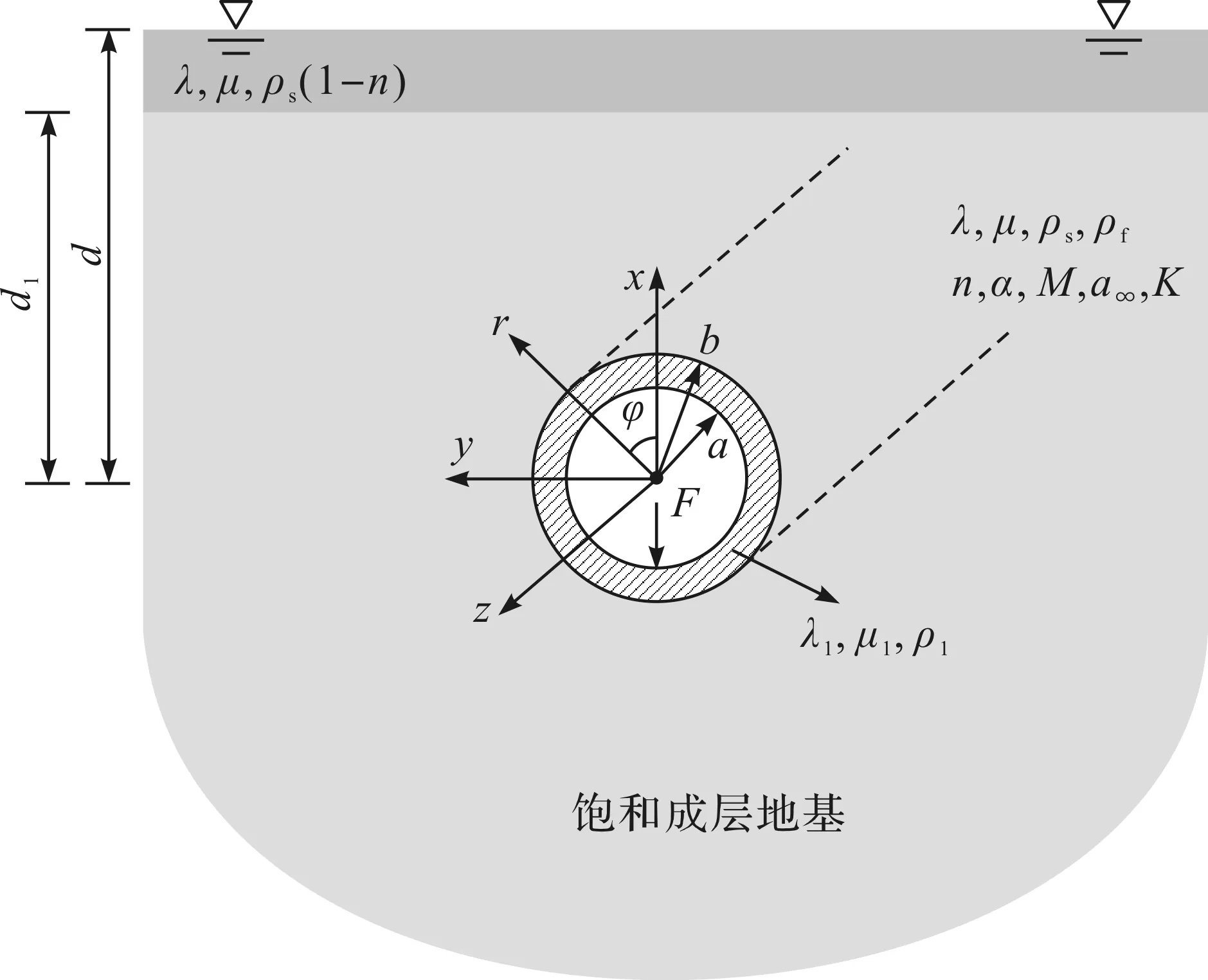
图8 考虑地下水位的成层半空间模型示意图

为研究地下水位变化对地表振动响应的影响，比较了以下3 种工况，工况I：水位位于地表(均质饱和半空间)；工况II：水位位于地下2 m(上覆干土层厚2 m+饱和下卧半空间)；工况III：不考虑地下水(干土均质半空间)。干土层密度ρe=1 500 kg/m3，阻尼系数0.04，Lamé常数λe=3×107Pa，μe=1.5×107Pa，下卧饱和两相介质的固体骨架和干土层具有相同的Lamé常数，固体颗粒密度ρs=2 500 kg/m3，孔隙流体密度ρf=1 000 kg/m3，孔隙率n=0.4，土相、流相混合密度ρ=ρs(1-n)+ρfn=1 900 kg/m3，渗透系数K=1×10-6(m3·s)/kg，曲折因子a∞=1，流体可压缩系数M=6.125×109N/m2，土颗粒压缩系数α=1。

不同地下水位下(工况I，II，III)地表观察点A和B的位移响应随荷载频率的变化规律如图9所示。由图9可知：在荷载频率较低时(低于15 Hz)，3 条曲线基本重合，说明地下水位的变化对低频地基振动影响较小；随着荷载频率的增大，可以发现当地下水位下降(工况I—工况II—工况III)时，地表振动响应呈现增大的趋势，工况I(水位位于地表)给出的地表响应最小。

图9 地下水位变化对地表A，B点位移响应的影响

为了进一步刻画地下水位变化对地表波动传播的影响，隧道正上方地表20 m×20 m范围内的竖向位移响应等高线云图如图10所示，荷载频率选取f0=40 Hz。由图10可知：随着地下水位下降(工况I—工况II—工况III)，整个地表的竖向位移响应显著增大，这是由于孔隙流体的饱和作用，降低了土体的可压缩性，使得地下水位较高时地基刚度较大，因此地下水位下降，地表振动响应增大。另外，3 种工况下地表均呈现出了规则的椭圆形波振面，这是由于波动在衬砌内的传播速度比在土体中快，因而隧道延伸方向波长较长，垂直于隧道方向的波长较短，表现出了规则的椭圆形波振面。

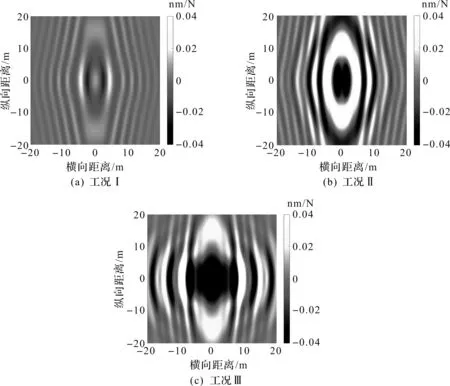
图10 地下水位变化对地表波动传播的影响

3 结 论

提出了地下移动荷载作用下成层半空间(弹性、饱和)中圆形衬砌隧道动力响应解析闭合解，该解适用于浅埋隧道的地铁环境振动预测，解决了以往近似解析解只适用于深埋隧道振动预测的问题。该解法显著优于现有的近似解析解，为地下交通荷载引起的环境振动问题提供了一套兼顾计算效率和精度的分析方法。通过数值算例，主要得出以下结论：1) 当地下移动荷载速度接近土体剪切波速时，三维半空间中衬砌隧道体系会发生共振，地表振动响应显著增大；2) 地基成层特性在高频范围内对地表振动响应具有显著影响；3) 在低频范围内，地下水位变化对地表振动影响较小，随着荷载频率的增大，地下水位下降可导致地表振动响应显著增加，在地铁振动预测中需要考虑地下水位变化对地基中波动传播的影响，以获得准确的振动预测值。