基于RSM和GA的涡轮熔模铸造工艺优化

蒋梦麒 ，何 博 ，姚定烨

（1.上海工程技术大学 材料工程学院，上海 201600；2.上海工程技术大学 高温合金精密成型研究中心，上海 201600）

0 引 言

浇注系统设计是熔模铸造设计过程中的重要部分，在熔模铸造时，浇注系统不仅是金属液进入型腔的通道，在铸件凝固过程中，浇注系统还起着补缩的作用，因此浇注系统的设计直接关系着熔模铸件的质量[1,2]。随着熔模精密铸件被广泛应用于航空航天、汽车及新能源领域，对熔模铸造产品的开发周期、开发成本与铸件成型质量提出了越来越高的要求[3-5]。

虚拟制造技术包括计算机辅助设计（CAD）、计算机辅助制造（CAM）与计算机辅助工程（CAE），是提升生产效率最有效的方法。徐文博等[6]利用数值分析软件ProCAST验证扩散器熔模铸件的初始浇注系统设计，并根据模拟结果优化了浇注系统设计，最终获得了合格的铸件。龚伟等[7]将光固化（SLA）快速成型技术与传统的砂型铸造相结合，利用数值模拟软件验证浇注系统设计与浇注工艺，最终将发动机缸盖铸件的孔隙率控制在10%以下，降低了铸造成本和缩短了生产周期。WANG D H等[8]将响应面分析法（RSM）与数值模拟技术相互结合，建立了二阶响应方程并以此为依据寻求最优工艺参数组合，实现了熔模铸件浇注系统设计快速优化。DONG C等[9]基于有限元模拟软件InterCAST利用遗传算法（GA）、果蝇优化算法（FOA）与内点法（IPOPT）快速优化冒口设计，模拟结果表明上述3种方法都可以较好地改善冒口设计以提升铸件的质量。

以下利用模拟软件ProCAST分析涡轮铸件在浇注过程中的温度场并预测缺陷的体积与分布情况，在有限元分析的基础上设计了RSM试验，分别构建了浇注系统半径、高度与浇注温度对涡轮铸件内部缺陷体积及缺陷与涡轮铸件表面距离之间的RSM函数，随后以二阶响应函数作为约束函数结合遗传算法优化涡轮熔模铸造最佳工艺设计。有限元模拟验证结果表明该方法可以获得无缺陷的涡轮铸件且其工艺出品率达到80.53%。

1 涡轮铸件浇注方案分析

涡轮结构较复杂，其三维模型如图1所示。涡轮最大直径为φ153 mm，高度为114 mm，13个相同的叶片沿着涡轮轴均匀分布，叶片为复杂曲面结构，其厚度为0.2～0.5 mm，涡轮体积为397 853.67 mm3。材料为IN718镍基合金，其化学成分如表1所示。

表1 IN718合金化学成分 质量分数

图1 涡轮三维模型

涡轮铸件采用熔模铸造方式进行成型，浇注参数为：浇注温度1 460℃，型壳预热温度1 100℃，保温3 h，真空浇注，浇注时间1 s。利用有限元软件ProCAST模拟浇注过程中的充型与凝固过程，在模拟时界面传热系数设置为：金属液与型壳之间的传热系数300 W/(m2·K)；型壳与空气之间的传热系数10 W/(m2·K)；环境温度20 ℃。

图2所示为涡轮铸件正置与倒置浇注方案的有限元模拟结果，根据实际经验，阈值取1%，即在该阈值下出现缺陷的概率为1%。图2（a）为正置浇注方案的凝固时间分布，该浇注方案的凝固方式是自底而上。涡轮短轴与较薄的叶片在较短的时间内先行凝固，而涡轮轴中部在顶端浇注系统的影响下凝固时间被延长，且在重力作用下可为先行凝固的底部提供金属液补缩，顶端浇注系统是最后凝固的区域。该浇注方案中的浇注系统可以调节温度梯度并为涡轮后凝固部分提供补缩，得到了无缺陷的涡轮铸件，使最终的缺陷残留在浇注系统内部，如图2（b）所示。倒置浇注方案的凝固时间分布如图2（c）所示，在该方案中涡轮的长轴被放置在叶片下方，长轴的凝固时间高于叶片与涡轮轴中部的凝固时间，导致在长轴凝固时铸件内部的补缩通道堵塞，浇注系统中储存的金属液难以提供补缩，最终在涡轮长轴中留下缺陷，如图2（d）所示。

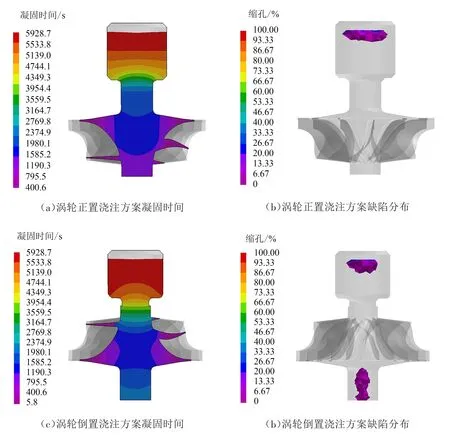
图2 凝固过程分析

2 响应面试验

2.1 Box-Behnken试验设计

虽然通过有限元模拟的温度场分析可以确定合理的浇注方案，但最佳的浇注系统设计应在得到无缺陷铸件的基础上拥有最大的工艺出品率。利用Box-Behnken试验方法进行试验设计，在试验中设计浇注温度T、浇注系统半径r与浇注系统高度h三个试验因素，其取值范围如表2所示，浇注温度为1 460～1 500 ℃，浇注系统半径为16～31 mm，浇注系统高度为58～70 mm。铸件中缺陷的体积V和缺陷与铸件上表面的高度H是2个响应目标。

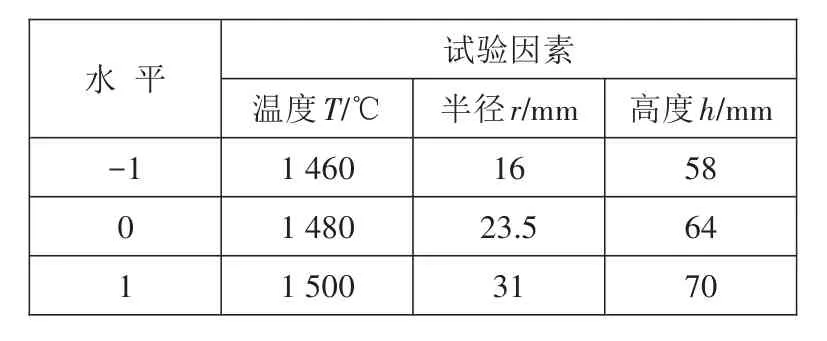
表2 试验因素水平表

利用Design-expert软件完成BBD试验方案的设计，该试验方案由12组正交试验与5组重复中心试验构成。利用有限元软件ProCAST模拟各组试验方案，得到的试验结果如表3所示，表中A、B、C分别表示试验因素T、r、h，Y1与Y2分别代表了2个响应目标V与H。

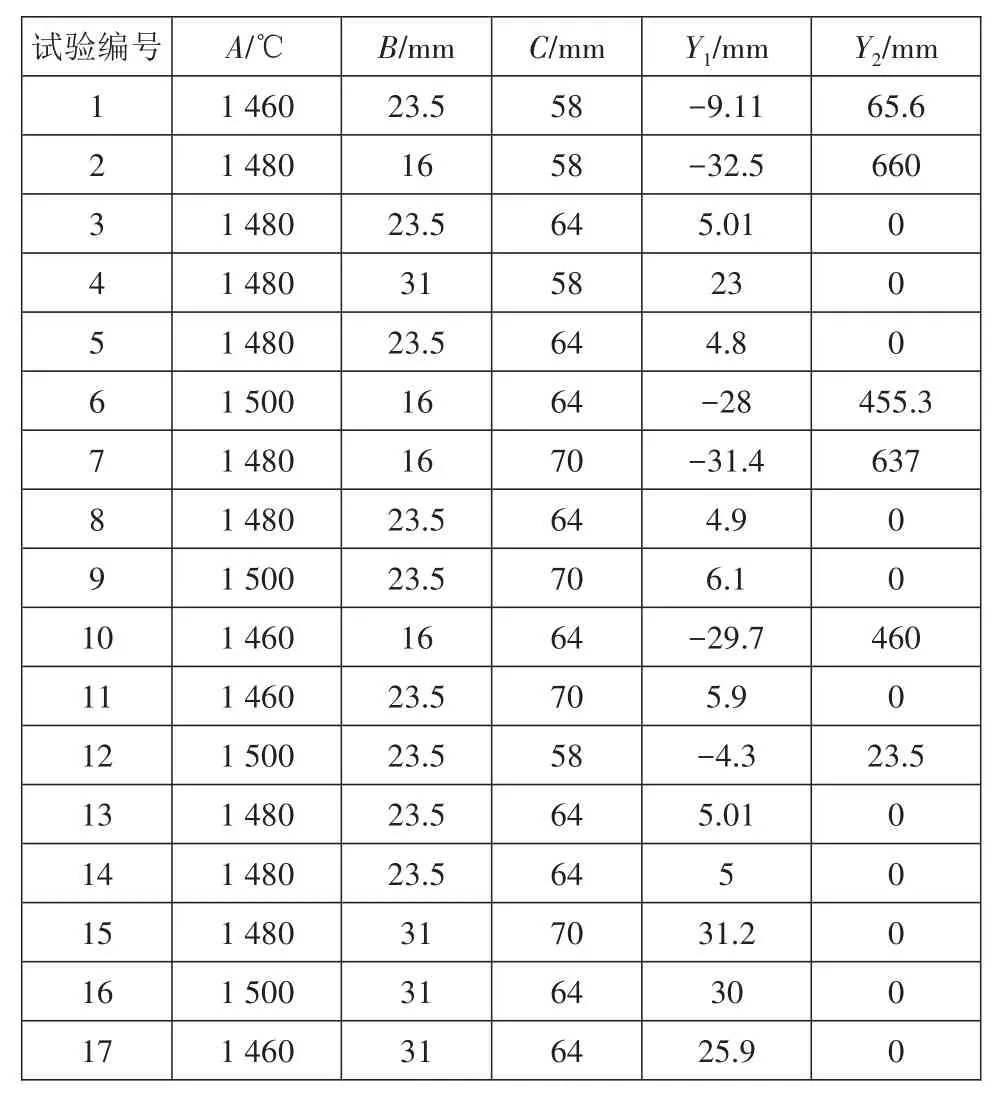
表3 试验方案与结果

2.2 响应面模型建立

依据试验结果构建了二阶响应面模型并对回归模型进行显著性检验和拟合缺失检验。模型的显著性以p值表示，p值越小代表模型越显著，即模型具有统计学意义；模型的拟合程度用R2表示，R2值越大代表模型的拟合程度越高。响应目标Y1的数学模型如式（1）中所示，模型中的p值小于0.05（即95%显著性水平）表明该模型具有统计学意义；拟合度R2为0.984 1接近于1，说明该模型的拟合精度较高。响应目标Y2的数学模型如式（2）中所示，模型p值小于0.05；拟合度R2为0.980 3接近于1，满足精度要。

利用建立的二阶响应方程可分别预测不同因子取值下响应目标Y1与响应目标Y2的值，如图3所示，横坐标为实测响应值，纵坐标为二阶响应方程计算得到的预测值，图中的点为数值模拟得到的响应目标值，斜率为1的直线表示在该处预测值等于实测值，由图3可知，实测点都分布在斜线周围，说明该二阶模型可信度较高，可用于进一步的优化。

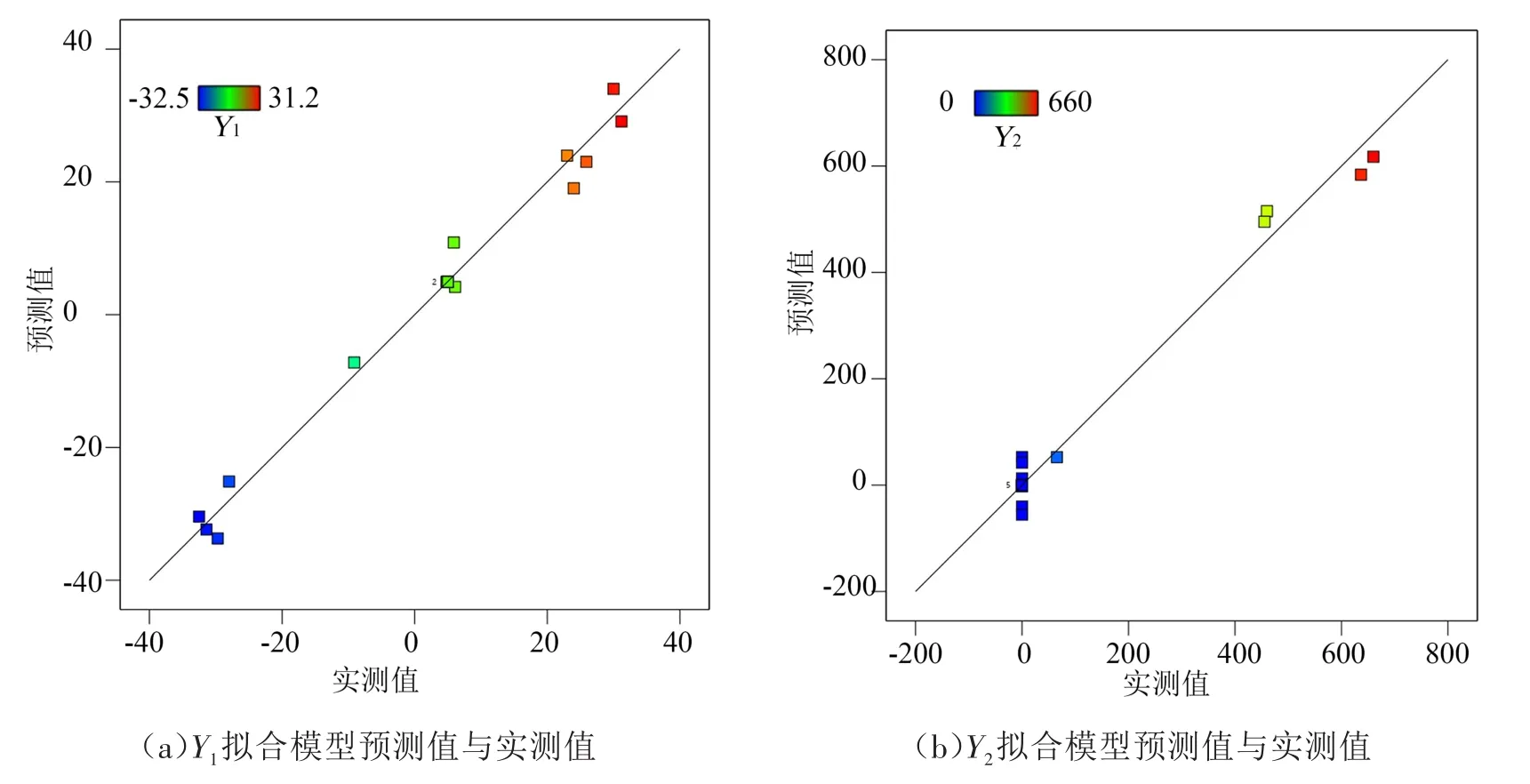
图3 预测值与实测值的比较

图4所示为三维响应面，可分别反映浇注温度（A）、浇注系统半径（B）、浇注系统高度（C）三个试验因素对缺陷距铸件表面高度（Y1）和铸件内缺陷的体积（Y2）两个响应目标的影响。从图4可看出，较高的浇注温度、较大的浇注系统半径与高度可以有效增大缺陷与铸件表面的距离并减少铸件内缺陷的体积。对比图4（a）～（c）可发现，对于响应目标缺陷与铸件表面的距离Y1，各因子的影响程度为B＞A＞C；同理，对比图 4（d）～（f）可看出，对于响应目标铸件中缺陷的体积Y2，各因子的影响程度为B＞C＞A。响应面的曲率反映了各因素对于响应值的权重。显然，图 4（a）～（c）中的响应面曲率小于图 4（d）～（f）中的响应面曲率，说明3个试验因子对于响应目标Y2的影响大于响应目标Y1。由此可得出结论：在涡轮浇注系统设计中，浇注系统的半径对铸件的成型质量起到了决定性的作用。

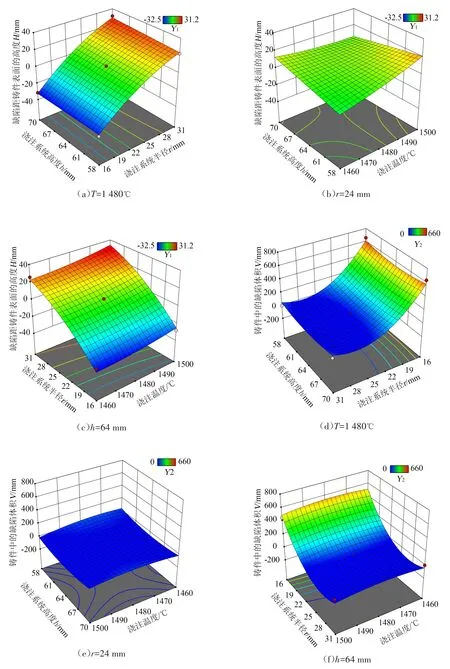
图4 试验因素与响应目标的互相影响

3 遗传算法优化

3.1 遗传算法

遗传算法（GA）的特点是利用简单的编码与繁殖机制反映复杂的问题，不受空间的限制性约束，可以从离散、多极值的问题中搜寻全局最优解。GA的计算流程如图5所示，在初始化产生种群后利用适应度函数评价初始种群中个体的优劣，选择适应度较高的个体进行交叉，变异操作产生下一代种群，新一代个体的平均适应度将会优于父体的适应度，最终在不断的迭代优化中接近最优解。

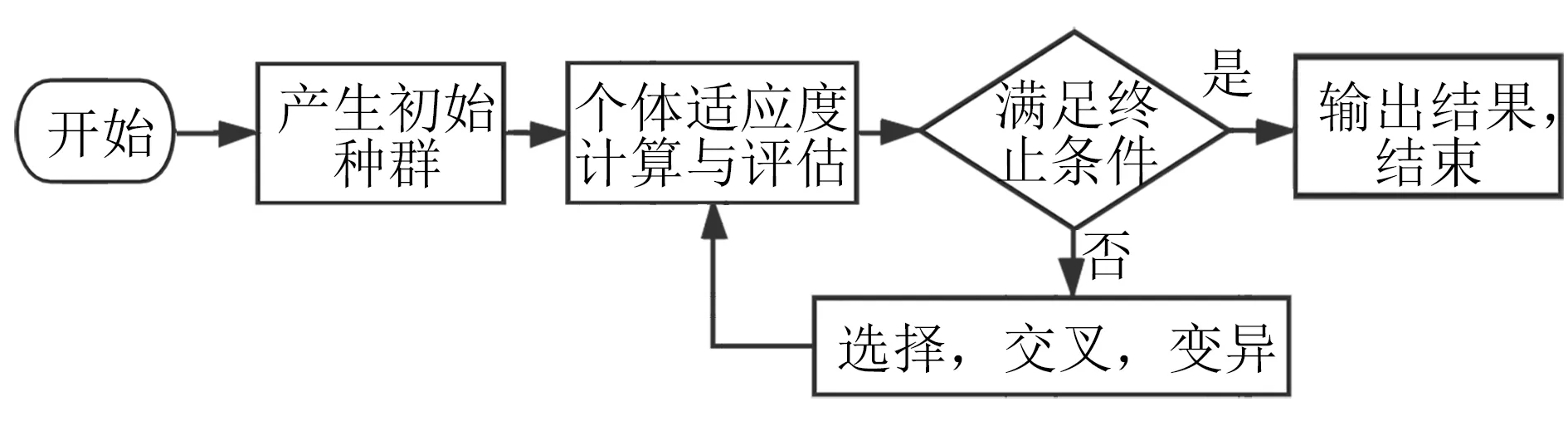
图5 遗传算法流程

3.2 目标函数

浇注系统设计目标是在消除铸件内部缺陷的同时拥有最大的工艺出品率，因此最小的浇注系统体积被用作目标函数，可由式（3）表示。

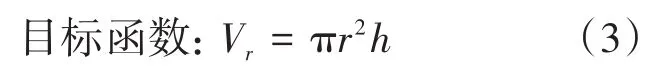
3.3 约束函数

在成型凝固完成时铸件内部缺陷的体积V=0，缺陷最后出现在浇注系统内部代表铸件被浇注系统完全补缩且铸件成型质量良好。二阶响应数学模型Y1与Y2将被作为约束函数来限制遗传算法的搜索空间，如式（4）所示。为了保证设计更合理，约束函数中设置了5 mm的安全距离来补偿Y1二阶响应数学模型中的误差。

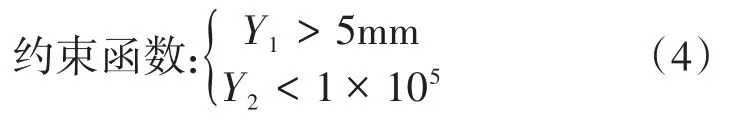
3.4 优化结果

利用进化算法工具箱Geatpy进行求解，设置参数如下：计算采用实数编码；初始种群大小设置为300；最大进化代数为500；计算采用赌轮盘选择算子；交叉方式为单点交叉，交叉概率为0.8；变异概率为0.05。迭代过程的进化曲线如图6所示，经28次迭代优化后种群收敛并获得全局最优解，最优个体目标值为96 217 mm3，对应的决策变量值分别为：浇注系统半径r=22.03 mm，浇注系统高度h=63.13，浇注温度1 500℃。

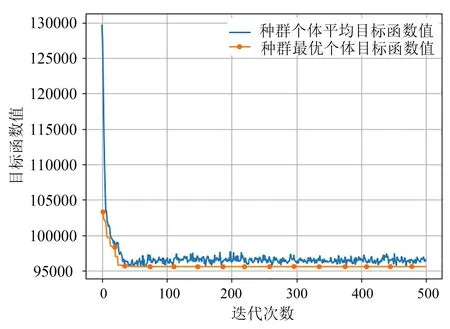
图6 迭代优化曲线

3.5 数值模拟验证

根据优化方案利用三维建模软件SolidWorks建立浇注系统模型并与涡轮装配，利用数值模拟软件验证优化方案，模拟时将浇注温度提升至1 500℃，不改变其余参数，优化结果如图7所示。图7（a）中的固相率为61%，此时涡轮叶片已接近完全凝固，涡轮短轴也由底部开始向上凝固，而涡轮轴中部与浇注系统内部的固相率分别约为53%与25%，即在此时涡轮内部的补缩通道仍然处于打开的状态，浇注系统中储存的金属液可以流经整个涡轮轴为短轴与叶片提供金属液补缩。当固相率达到85%时涡轮处于凝固完成阶段，如图7（b）所示，此时浇注系统中心的固相率为53.3%～60%，仍存在一定的补缩能力。图7（c）所示为完全凝固时间分布，可明显看出铸件整体的凝固情况。涡轮叶片最薄部分最先凝固，完全凝固时间约为890 s；涡轮轴由下而上凝固，涡轮短轴完全凝固时间约为1 600 s，长轴顶部凝固完成的时间约为1 700 s；浇注系统完全凝固的时间大于1 738 s。最终缺陷分布如图7（d）所示，缺陷留在了浇注系统中，且缺陷与铸件之间的距离约为3 mm。该结果与预期一致，此时设计的浇注系统处于临界状态，若降低设计因子中的任何一个目标都可能会导致缺陷进入涡轮铸件内部，该浇注系统的设计工艺出品率为80.53%。

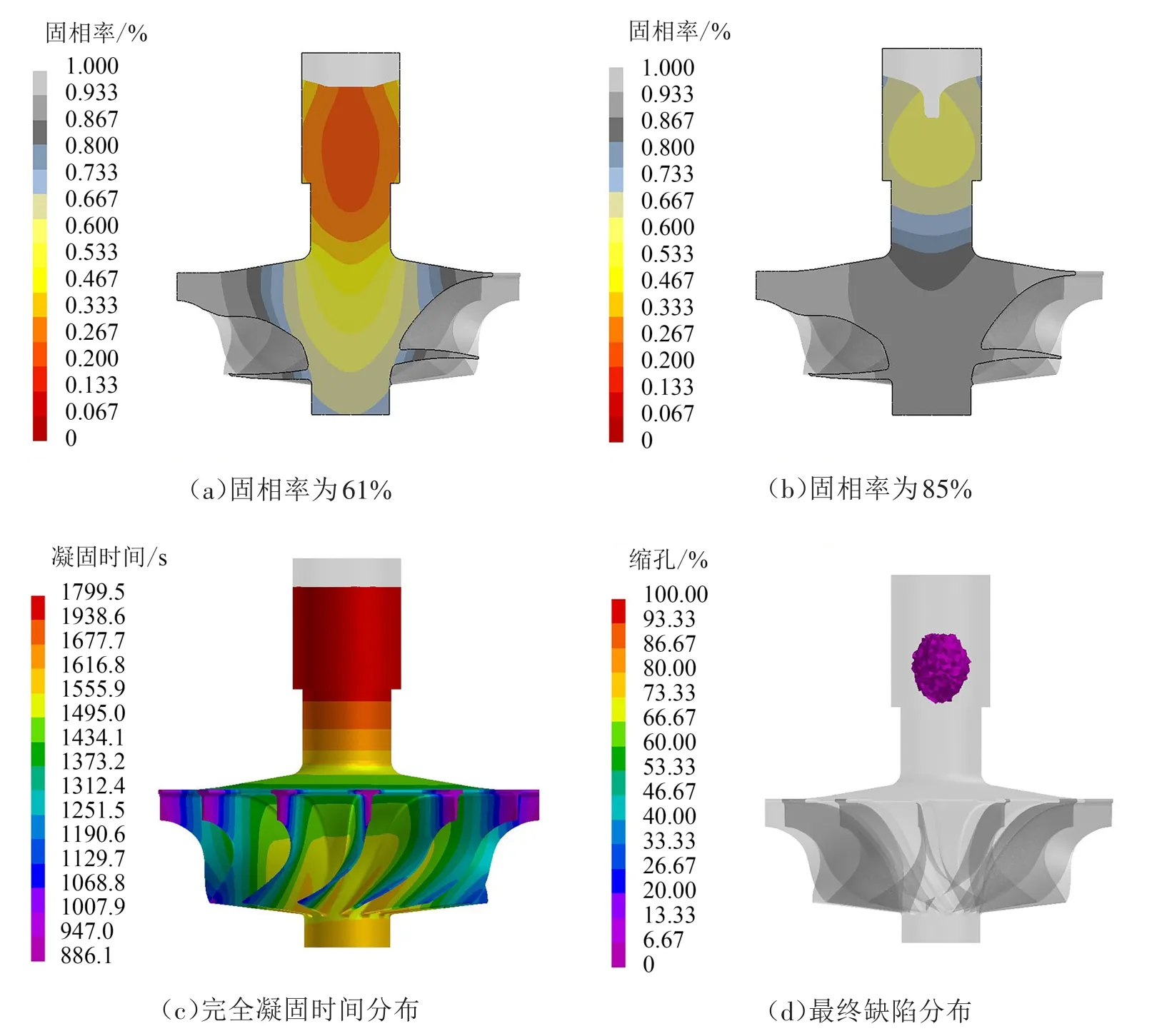
图7 优化方案的凝固过程模拟与缺陷分布

4 结束语

将响应面分析法（RSM）与遗传算法（GA）相结合，提出了一种涡轮浇注系统设计优化的方法。利用RSM-BBD法建立了2组二阶响应方程来预测铸件内部缺陷的大小与缺陷距铸件的表面距离，并以二阶响应方程为约束函数建立浇注系统设计的数学模型，最后利用遗传算法得到工艺出品率为80.53%的浇注系统设计方案组合：浇注温度为1 500℃，浇注系统半径为22.03 mm,浇注系统高度为63.13 mm，数值模拟分析的结果表明，在该浇注方案下可以获得无缺陷的涡轮铸件。经总结得出如下结论。

（1）结合RSM与有限元分析技术相结合可快速计算铸造过程中的缺陷模型以及各参数对最终铸件成型质量的权重。

（2）在涡轮熔模铸造浇注系统设计中，浇注系统半径对涡轮铸件内部缺陷的体积与最终缺陷的位置有较大的影响，浇注系统高度与浇注温度对上述2个目标也有影响，但影响不大。增加浇注系统半径是提升涡轮熔模铸件成型质量最直接也是最有效的方法。