矩阵半张量积在求解复线性系统的特殊Toeplitz解中的应用

丁文旭，李 莹，王 栋，王 涛

(聊城大学 数学科学学院，山东 聊城 252059)

0 引言

对于多线性乃至非线性系统问题计算的数值方法,矩阵表示一直是一个无法绕行的瓶颈问题。对此,程代展研究员提出了矩阵半张量积这一有利工具。相比矩阵普通乘法,矩阵半张量积打破了矩阵维数的限制,并且满足准交换性。 目前,矩阵半张量积的应用越来越广泛,函数矩阵微分、非线性多元映射的泰勒展式、向量场和函数等运算都可通过矩阵半张量积来实现[1]。此外,在非线性控制系统的对称性[2,3]、非正规反馈线性化[4]、布尔网络的拓扑结构[5,6]、系统的能控能观性的判断[7]、布尔网络的稳定和镇定设计最优问题[8]、图染色[9]以及博弈论的逻辑动态过程和策略最优化[10]等问题的研究中均体现出矩阵半张量积的合理性、有效特殊型矩阵在许多领域有广泛的应用,其中形如性和优越性。本文将半张量积的应用范围进一步拓展到复线性矩阵方程的特型解的计算问题中。

的矩阵被称为Toeplitz矩阵,其在工程中有大量应用。例如,在雷达、声呐探测等目标定位领域,有赖于利用Toeplitz矩阵将阵列观测数据的相干函数进行重排,构造一满秩的Toeplitz矩阵,再利用奇异值分解来提高对相干信源的DOA估计性能[11]; 利用四元数Toeplitz矩阵重构算法解决电磁矢量阵列的相干信源波达方向估计[12],此外,在偏微分方程和卷积型积分方程的求解、pade逼近和控制理论中的最小实现问题中也起着十分重要的作用[13]。

线性矩阵方程可以被用来解决结构设计、振动分析、自动控制等诸多实际问题,关于矩阵方程的理论及算法已有大量的文献[14-16]。例如对于矩阵方程的Toeplitz解,应用格点滤波理论导出了一种递推解法[17],利用矩阵的Kronecker积、Vec算子和MP广义逆给出了AXB+CYD=E的Toeplitz矩阵解和对称Toeplitz矩阵解的表达式等[18]。本文利用矩阵半张量积研究复矩阵方程AX=B的下上三角形Toeplitz解。

本文内容安排,第1部分给出所需的预备知识,第2部分提出关于复向量、复矩阵的新的实向量表示并研究其运算性质,第3部分,结合复矩阵的实向量表示和矩阵半张量积研究问题1、2的解，第4部分,给出算法及数值例子检验方法的有效性,最后,第5部分总结全文。

1 预备知识

定义1[19]设A∈Rm×n,B∈Rp×q,n与p的最小公倍数为t=lcm(n,p),则A与B的半张量积定义为A×B=(A⊗It/n)(B⊗It/p)。

当n=p时,A与B的半张量积转化成A与B的普通乘积。

半张量积具有如下性质。

定理1[20]设x∈Rm,y∈Rn,则x×y=x⊗y。

定理2[21]设x∈Rm,A为任意实矩阵,则x×A=(Im⊗A)×x。

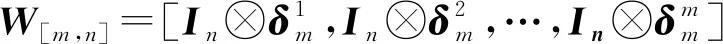
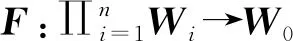
MF称为F的结构矩阵。

2 复矩阵的实向量表示及性质

本节我们将提出复矩阵的实向量表示的概念。为此,首先定义复数的实向量表示。

定义3 设x=x1+x2i∈C,记vR(x)=(x1,x2)T,称vR(x)为复数x的实排列式。

利用矩阵半张量积,可将两复数相乘的实排列式利用两复数的实排列表示。

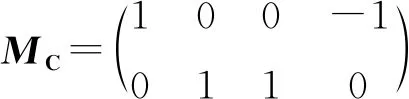
相仿地,可以定义复向量的实排列。

定义4设x=(x1,x2,…,xn),y=(y1,y2,…,yn)T为复向量,分别称

为复向量x和y的实排列。

下面利用复向量的实排列定义复矩阵的实向量表示的概念。

定义5设A∈Cm×n,Colj(A)(1≤j≤n),Rowi(A)(1≤i≤m)分别表示A的第j列和第i行,称

分别为复矩阵A的实列排及实行排。

我们提出并证明复向量和复矩阵的实向量表示的如下性质。

(2)vR(ax)=avR(x),

证明(1),(2)显然成立。下面仅证性质(3)。利用定理4,可得

vR(xy)=vR(〗x1y1+x2y2+…+xnyn)

=MC×v(x1)×vR(y1)+…+MC×vR(xn)×vR(yn)

=MC×[v(x1)×vR(y1)+…+vR(xn)×vR(yn)]

其中

证明(1)-(3)显然成立,仅证(4)。记

则有

3 问题1、2的解

定理8设A,B∈Cm×n,AX=B有下三角Toeplitz解当且仅当

(1)

(2)

证明X为复矩阵方程AX=B的下三角Toeplitz解,可以得到

‖AX-B‖=0,

利用MP逆的性质得

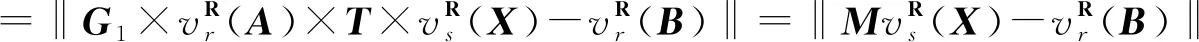
类似的可以得到问题2的解,证明过程省略。

定理9设A,B∈Cm×n,AX=B有上三角Toeplitx解当且仅当

(3)

极小范数上三角Toeplitz解XU满足

(4)

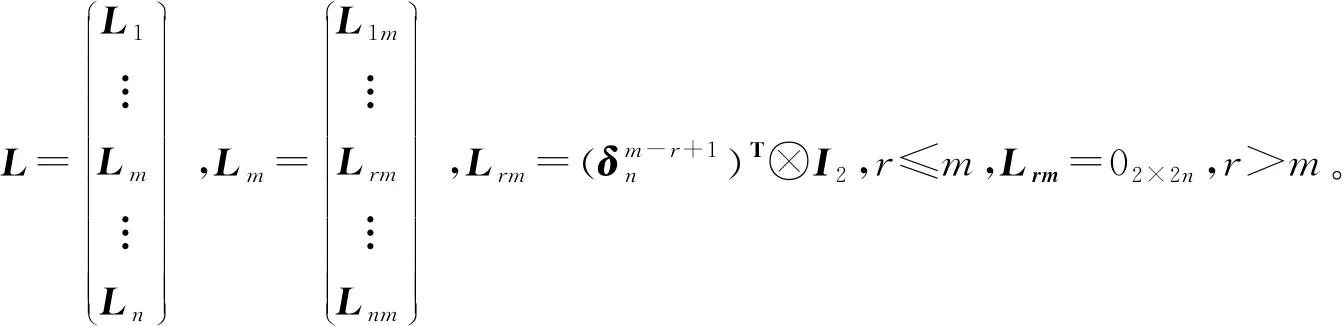
4算法及数值例子

算法1(问题1)设AX=B满足具有下三角Toeplitz解的条件，本算法用于计算极小范数下三角Toeplitz解。

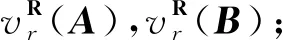
(2) 输入G,T,输出矩阵M;

(3) 根据(2),输出问题1的极小范数下三角Toeplitz解XL的有效元素实排列结果,可进一步得到XL。

算法2(问题2)设AX=B满足具有上三角Toeplitz解的条件，本算法用于计算极小范数上三角Toeplitz解。

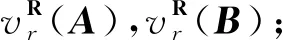
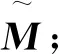
(3) 根据(4),输出问题2的极小范数上三角Toeplitz解XU的有效元素实排列结果,可进一步得到XU。

算例1考虑复矩阵方程AX=B的下、上三角形Toeplitz解,不妨令m=n。A在Matlab中利用‘rand’随机生成:A=rand(n)+rand(n)i。 随机生成两个向量,利用‘Toeplitz’及Tril(Triu)生成下上三角形Toeplitz矩阵XL(XU)。计算B=AX,n=5k(k=1:8)。

图1 下三角形Toeplitz解的误差

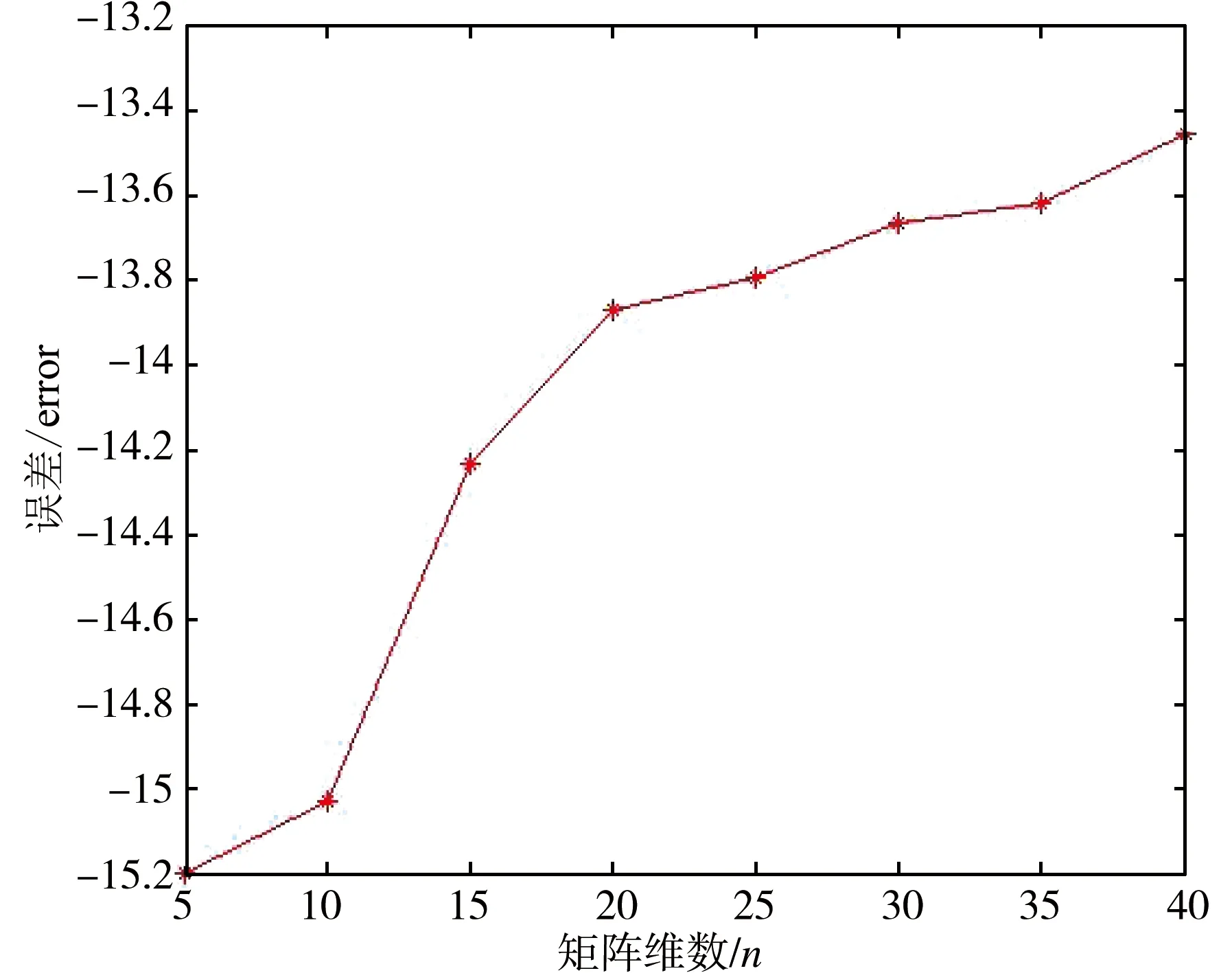
图2 上三角形Toeplitz解的误差

由图中数据可以看出,利用算法1和2所得的不同规模的矩阵方程的解的误差的数量级均小于-13,充分说明了该算法的有效性。

5 结论

本文介绍了基于矩阵半张量积求解复线性系统AX=B的三角形Toeplitz解的新方法。利用复矩阵的实向量表示,将复矩阵方程转化为实矩阵方程,进而给出AX=B的上、下三角形Toeplitz通解的表达式。利用数值例子验证了这种方法的有效性。该方法还可以应用于其他多种代数结构上线性系统的特型解的计算,为矩阵半张量积在数值分析领域寻找到了新的应用价值。