证券市场波动率分析的PSO-ICA-GARCH模型

周晓玲， 王小侠

(西安理工大学 理学院， 陕西 西安710054)

对单个资产的收益波动率和多个资产之间的条件协方差矩阵(通常也称为多元波动率)的研究[1-4]是当前金融计量学领域的重要内容。主要的多元波动率模型有BEKK模型[5]、常值条件相关系数(CCC-GARCH)模型[6]、动态条件相关系数(DCC-GARCH)[7]模型等。在资产组合维数较高的情况下，上述多元波动率模型均存在待估参数数量巨大的问题。为了解决增加变量引起维数灾难的问题，在多元波动率模型中引入了一系列降维思想。Alexander[8]将主成分分析引入了多元波动率建模，提出了O-GARCH模型，该模型通过主成分分解将一组变量的条件协方差矩阵的问题转化成了分别考虑它们主成分的一元波动率的问题。但O-GARCH模型中采用的假设“主成分之间的条件协方差矩阵是对角阵”通常是不成立的，因为主成分之间的无条件不相关并不意味着条件不相关。2005年Wu等[9]将独立分量分析(independent component analysis，ICA)引入多元波动率建模，对纽约和香港的股票市场进行实证分析时，将残差序列用ICA进行分解，然后对得到的独立成分分别建立GARCH模型。结果表明该方法对多只股票的收益率波动的估计方面比用PCA方法分解残差更有效，该模型为资产组合的选择和风险管理提供了新思路，且这种方法是基于独立分量的单变量GARCH模型，故计算成本很低。2012年García-Ferrer等[10]提出了一个新的条件异方差因素模型GICA-GARCH模型，该模型结合了ICA和多元GARCH(MGARCH)模型。GICA-GARCH模型使用单变量ARMA-GARCH模型将独立成分的估计与其拟合分开。并且通过马德里股票市场的经验应用评估得出GICA-GARCH比CUC-GARCH和O-GARCH模型有更强的一步波动率预测能力。2018年刘鑫[11]研究了基于ICA的多元波动率模型，探讨了ICA在证券市场的收益率序列波动率建模中应用的可行性及模型的拟合与估计效果的优势。2018年Lin[12]利用GARCH类型模型研究上证综合指数的计量经济学特征,比较发现EGARCH(1,1)(非对称)的拟合和预测性能总体上优于GARCH(1,1)(对称)和TARCH(1,1)模型。

但ICA多采用梯度算法对目标函数进行优化来确定最优解，梯度算法具有收敛精度低、可能陷入局部最小点等缺点。而粒子群算法(particle swarm optimization，PSO)因其建模简单、适用性广、全局寻优能力强等优点可用来解决以上问题。在构造投资组合或进行资产配置的时候，协方差矩阵是构造有效边界的主要参数，故提出了各类不同的关于波动率的动态计量模型[13]和预测方法。

1 PSO-ICA算法

1.1 算法构造及步骤

传统的ICA是指从线性混合的数个统计独立的源信号的混合信号中分离出源信号的一种技术。观测信号x(t)是多个独立信源s(t)经混合矩阵A组合而成。ICA的任务是在s(t)与A均未知的条件下，求解一个解混矩阵W，使得x(t)通过它后的输出y(t)是s(t)的最佳逼近。该算法确定解混矩阵的过程可以看作是对某一独立性判据进行寻优，使各分量之间达到相互独立的过程，等价于PSO算法的目标函数和优化算法，因此可以将PSO算法引入ICA算法中，将负熵

J(y)∝[E{G(y)}-E{G(v)}]

(1)

最大化作为目标函数，其中v是与y具有相同方差的零均值Gauss变量，E为均值运算，G为非线性函数。利用PSO算法粒子全局寻优的方法替代ICA的梯度算法，将满足目标函数和最大迭代次数得到的全局最优位置向量作为解混矩阵W的一行，依次更新循环得到解混矩阵W。

PSO-ICA算法步骤为如下。

Step1.对观测信号X′中心化得到均值为0的信号X：

X=X′-E(X′)

(2)

白化信号X使其具有单位方差且不相关：

Z=D-1/2PTX

(3)

其中D和P分别是X的协方差矩阵的特征值矩阵和特征向量矩阵.

Step2.设定初始随机解混矩阵W=[W1,W2,…,Wm]T。

Step3.当p=1时，以初始随机解混矩阵W的行数m和列数d分别作为PSO算法中粒子的个数和维数,以Wi=[wi1,wi2,…,wid]作为粒子的位置向量，随机初始化每个粒子的速度Vi=[vi1,vi2,…,vid]，其中i=1,…,m。

Step4.给出最大迭代次数T及评价的适应度函数为:

(4)

其中Yi=WiZ，存储每个粒子的最大适应度值和位置pi，并从群体中选取最大的适应度值及其位置pg。

Step5. 进行每一代粒子速度和位置的更新：

(5)

式中：c1和c2为学习因子，本文均取2；rand1和rand2为[0,1]内的随机数。

Step6.判断是否达到预定的迭代次数，如果没有达到，返回Step 4；如果达到，停止迭代，输出最优的位置向量Wp。

Step7.对解混矩阵W进行正交和归一化处理，避免分离同一信号以及保证分离的稳定性。

Step8.判断W是否所有行向量完成运算。令p=p+1，若p≤m，返回Step 3；反之，停止循环，确定分离矩阵W。

Step9.输出分离信号Y=WZ。

1.2 实验分析

实验中分别选取信号点数为200的正弦信号s1、方波信号s2、锯齿形信号s3、随机信号s4作为检测信号，检验PSO-ICA算法的有效性。图1是FastICA算法和PSO-ICA算法的分离结果。表1是分离结果的信噪比，表2是两种方法分离结果的相关系数。

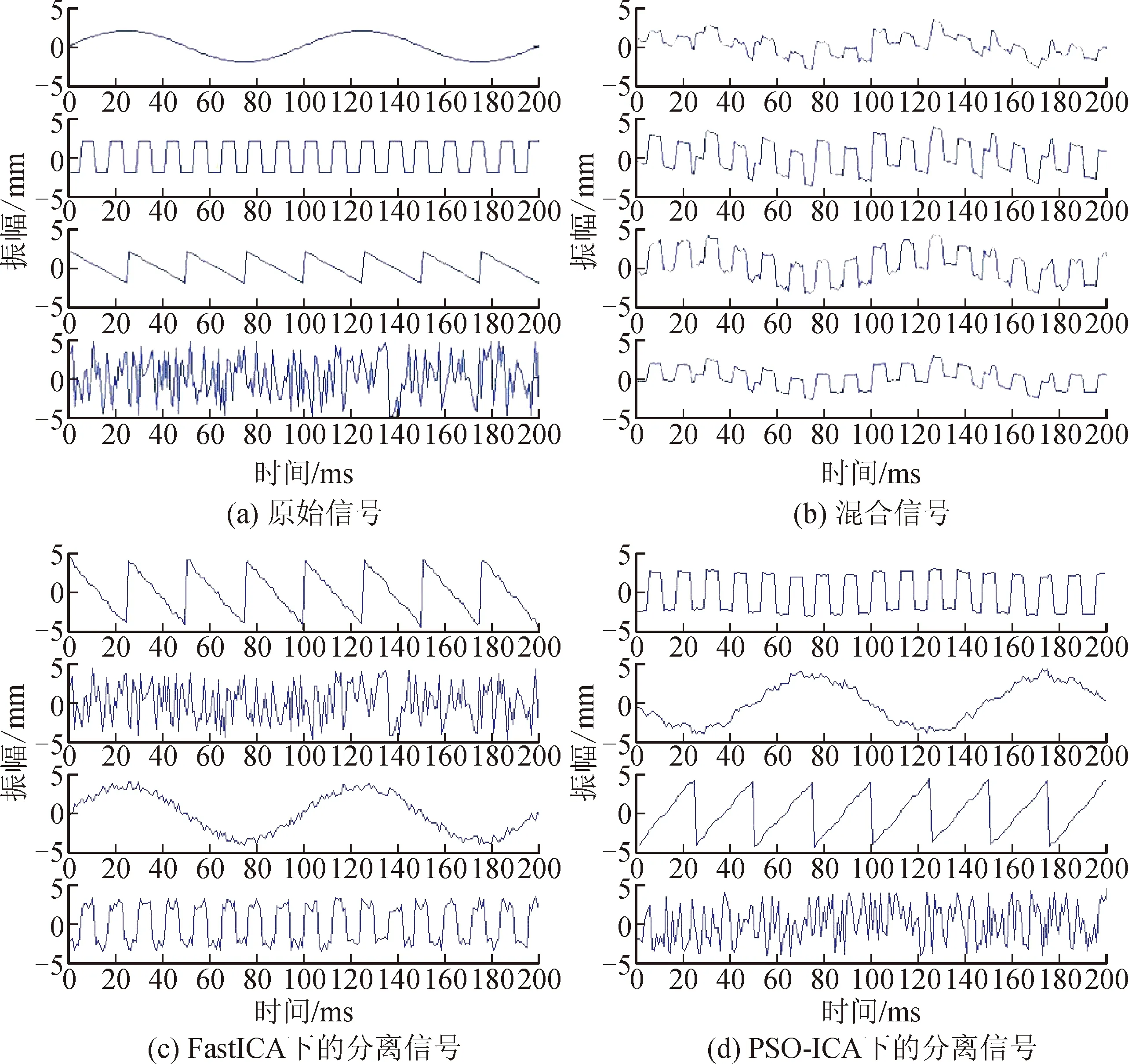
图1 FastICA和PSO-ICA实验结果图Fig.1 Experimental results of FastICA and PSO-ICA

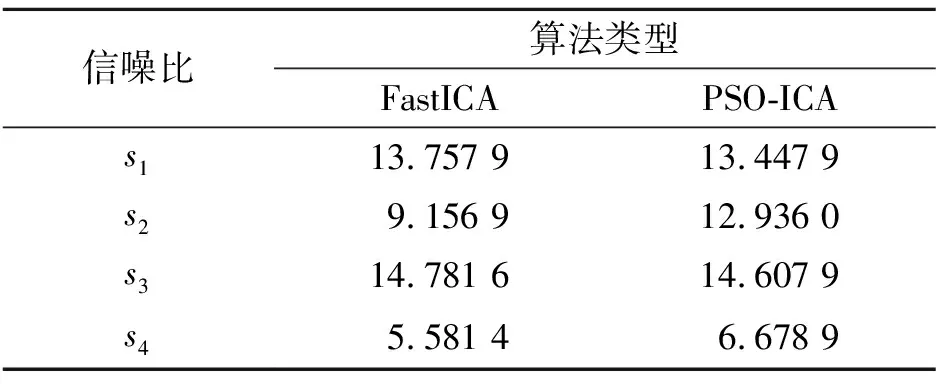
表1 FastICA和PSO-ICA算法的信噪比Tab.1 SNR of FastICA and PSO-ICA algorithms

表2 原始信号与分离信号的相关系数Tab.2 Correlation coefficient of originalsignal and separated signal

由图1可以看出，与FastICA相比PSO-ICA具有较好的分离效果,尤其在方波形信号中效果更加明显。需要指出的是分离结果显示分离信号顺序与原始信号顺序出现不同，并且某些信号与原始信号反相，这是由ICA算法所固有的分离信号的排列次序和波形的幅度与相位的不确定性引起的，并不影响信号的提取。

在同一混合矩阵下，分离信号与原始信号的信噪比参数越大表明分离的效果越好。由表1可以看出，s1和s3相近，但PSO-ICA算法的s2和s4均远大于FastICA算法的信噪比,说明PSO-ICA分离结果的信噪比更高。

由表2可以看出，两种方法关于正弦信号和锯齿信号的相关系数相近，但对方波信号和随机信号，PSO-ICA算法对应的相关系数明显大于ICA算法的相关系数，更接近于1，说明PSO-ICA算法具有更高的分离精度，分离效果更好。

综合图1、表1和表2，不难看出，无论从视觉直观还是数据客观角度，都显示出PSO-ICA比FastICA有更好的分离效果，因此在接下来的工作中我们选择PSO-ICA算法进行股票收益的多元波动率建模。

2 PSO-ICA-GARCH模型

2.1 模型原理

对股票收益进行多元波动率建模时，O-GARCH模型假设各主成分之间弱相关，在实证分析时，往往会产生预测效果和实际情况不相符的问题。

ICA-GARCH模型中ICA算法存在收敛精度低及容易陷入局部最优的问题。本文将PSO-ICA算法与GARCH模型结合构造PSO-ICA-GARCH模型，可以有效克服如上问题。

PSO-ICA-GARCH模型首先通过PSO-ICA算法将股票收益率序列rt分解为相互独立的成分st，即如果存在矩阵A以及d维向量st=(s1t,s2t,…,sdt)，其中对每个时刻t,sit和sjt(i≠j)都是相互独立的，使得(1)成立，则称st是rt的d个独立成分，此时条件协方差矩阵Vt是一个对角阵，且PSO-ICA算法假设独立成分是服从非Gauss分布的，这更符合金融时间收益率序列数据的特性，然后对每个独立成分sit进行单元GARCH建模，最后表出收益率序列rt的条件协方差矩阵Ht。

PSO-ICA-GARCH(1,1)模型如下：

rt=Ast

(6)

sit=vitαit,αit～i.i.d(0,1)

(7)

(8)

式中：A为混合矩阵；{sit}为独立成分；vit为独立成分{sit}的方差；Vt是由vit组成的对角矩阵。则收益率序列rt的条件协方差矩阵为Ht=AVtAT。

式(6)将收益率序列由PSO-ICA算法转换为独立成分，式(7)～(8)是对独立成分的一元GARCH模型估计。

2.2 模型算法步骤

Step1.对各股收盘价格进行取对数差分处理后得到对应的收益率序列。

Step2.作各股收益率序列图，观察其是否表现出尖峰厚尾和聚集性等特征。

Step3.对各股收益率序列的相关统计特征进行分析，如峰度、偏度、正态分布检验(J-B检验)和平稳性验(ADF检验)。

Step4.判断各收益率序列是否具有自相关性，若有采用AR模型去除其自相关性。

Step5.判断各股残差序列是否具有ARCH效应。

Step6.剔除掉没ARCH效应的收益率序列，对满足条件的对数收益率序列采用PSO-ICA算法，对得到的独立成分分别进行单元GARCH模型拟合和预测。

Step7.对PSO-ICA-GARCH模型进行拟合和预测效果检验。

3 实证分析

3.1 数据选取

概念股作为一类共同特征股票的总称它们收益率的波动往往受市场同一因素的影响，其价格波动也存在着一定的共性，故本文随机选取5支阿里巴巴概念股进行实证研究。分别是万隆光电、海尔智家、视觉中国、分众传媒和华胜天成股票，从2018年1月2日到2019年12月31日为期487天收盘价交易数据，对各股收盘价格进行取对数差分处理后得到对应的对数收益率序列：

ri,t=lnpi,t-lnpi,t-1

(9)

式中：pi,t为第i只股票t时刻的收盘价格；ri,t表示第i只股票t时刻的对数收益率，并做百分比处理。

3.2 数据的统计性质

表3给出了五支股票收益率数据的统计性质。可以看出，海尔智家的收益率均值为正值，说明这支股票当期收益处于盈利状态，其它四支股票的收益率均值都为负值，说明当期股票处于亏损状态。

表3 对数收益率序列统计性质Tab.3 Statistical properties of logarithmic return series

标准差代表各支股票收益率的风险大小，海尔智家当期盈利较多且相应的风险最小，分众传媒当期亏损最大，但风险相对较小，万隆光电当期亏损最小，但是风险最大。

其中各股对数收益率序列的偏度不为0，海尔智家、视觉中国和分众传媒对数收益率序列的偏度都大于0为右偏，剩余两支股票的对数收益率序列表现出一定程度的左偏。

各股对数收益率序列的超额峰度均大于0，表现一定程度的厚尾性，其中海尔智家对数收益率序列的厚尾性最为明显，且J-B统计量对应p值接近于0，故拒绝收益率序列为正态分布的原假设，即各股对数收益率数据都表现出尖峰厚尾的背离正态分布的性质。

ADF检验对应的p值均小于显著性水平0.01，故拒绝各支股票的对数收益率有单位根(非平稳序列)的原假设，故这5支股票的对数收益率序列皆是平稳序列，可以直接进行模型估计。

3.3 自相关性检验

自相关就是随机扰动项的各个值之间存在着相关关系。自相关性会致使模型的参数估计发生偏差，得不到有效无偏的最优估计。对选取的五支股票的对数收益率序列进行自相关检验，结果显示各支股票的日收益率序列在高阶滞后阶时恰好均无自相关性。

需要说明的是：若收益率序列具有自相关性，需用AR模型去除其自相关性。

3.4 ARCH效应检验

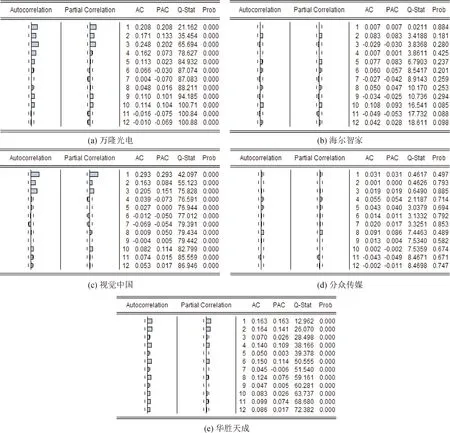
图2 各股收益率残差平方序列的自相关检验图Fig.2 Autocorrelation test chart of the square series of the return of each stock

从图2可以看出，海尔智家和分众传媒的对数收益率残差平方序列在各滞后阶下，均在0.05的显著性水平下接受原假设，即收益率残差平方序列不具有自相关性，也即不具有ARCH效应；万隆光电、视觉中国和华胜天成的对数收益率残差平方序列在各滞后阶下存在自相关性，则这三支股票具有很强的ARCH效应，可以进行GARCH建模。

3.5 模型参数估计与模型检验

由表3可知，所选取的这三支阿里巴巴概念股的对数收益率数据均不服从正态分布，因此在对收益率序列进行O-GARCH、ICA-GARCH和PSO-ICA-GARCH建模时，采用t分布可以更好地刻画序列的特性。用PCA、ICA和PSO-ICA算法对三组收益率序列提取主成分和独立成分，然后分别对三组主成分和独立成分进行GARCH(1,1)模型拟合，结果见表4，表5和表6,其中***，**，*分别表示在显著性水平1%、5%和10%下显著。

表4 O-GARCH(1,1)模型的参数估计Tab.4 Parameter estimation of O-GARCH (1,1) model

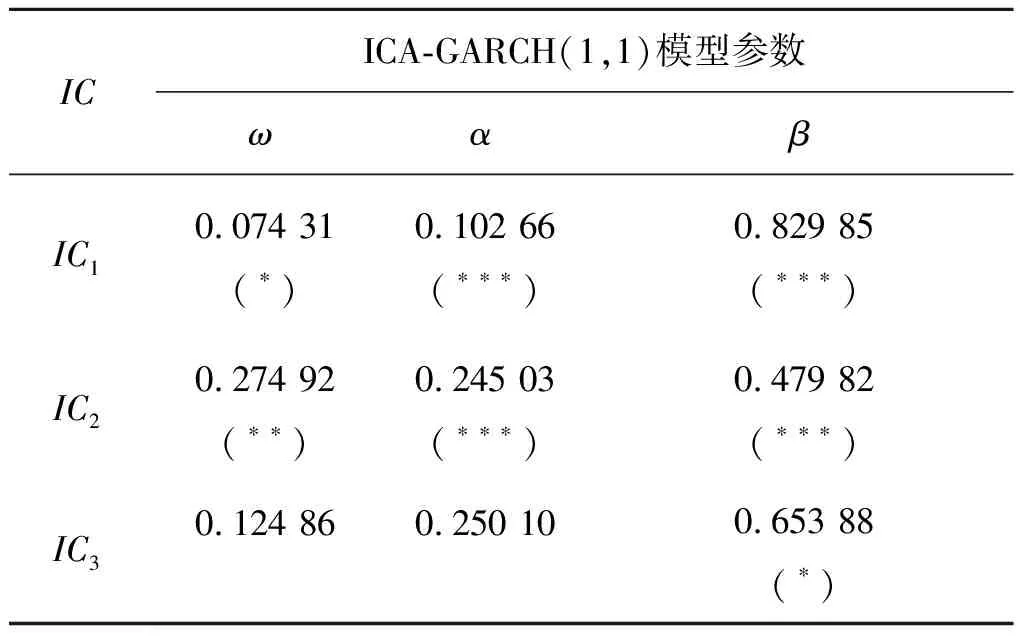
表5 ICA-GARCH(1,1)模型的参数估计Tab.5 Parameter estimation of ICA-GARCH (1,1) model

表6 PSO-ICA-GARCH(1,1)模型的参数估计Tab.6 Parameter estimation ofPSO-ICA-GARCH (1,1) model

用模型O-GARCH、ICA-GARCH和PSO-ICA-GARCH对收益率序列进行主成分和独立成分提取时，转换矩阵分别为W1、W2和W3：

(10)

(11)

(12)

表7 O-GARCH、ICA-GARCH和PSO-ICA-GARCH模型检验结果比较Tab.7 Comparison of test results of O-GARCH、ICA-GARCH and PSO-ICA-GARCH models

由表7可以看出，三种模型的F1统计量在0.01的显著性水平下均显著，三种模型拟合效果较一致。F3统计量中只有O-GARCH模型在0.1的显著性水平下显著，其它两种模型均不显著，说明ICA-GARCH模型和PSO-ICA-GARCH模型的拟合效果均优于O-GARCH模型。F2统计量中PSO-ICA-GARCH模型在t分布下是在0.05的显著性水平下显著，且PSO-ICA-GARCH模型中统计量的值明显小于其它两个模型，说明PSO-ICA-GARCH模型的拟合效果明显优于其它两种模型。综上所述，PSO-ICA-GARCH模型相较于O-GARCH和ICA-GARCH模型，具有更好的模型拟合效果。

3.6 模型预测效果比较

参照Pelletier[15]的做法，用自适应平均绝对偏差(adaptive mean absolute deviation，AMAD)检验预测效果，其定义为：

(13)

式中m的作用是对随机的误差进行平均处理。

当m=0时，三种模型向后5步预测的AMAD值和预测效果分别见表8和图3。

表8 O-GARCH、ICA-GARCH和PSO-ICA-GARCH模型的预测效果Tab.8 Prediction results of O-GARCH,ICA-GARCH and PSO-ICA-GARCH models

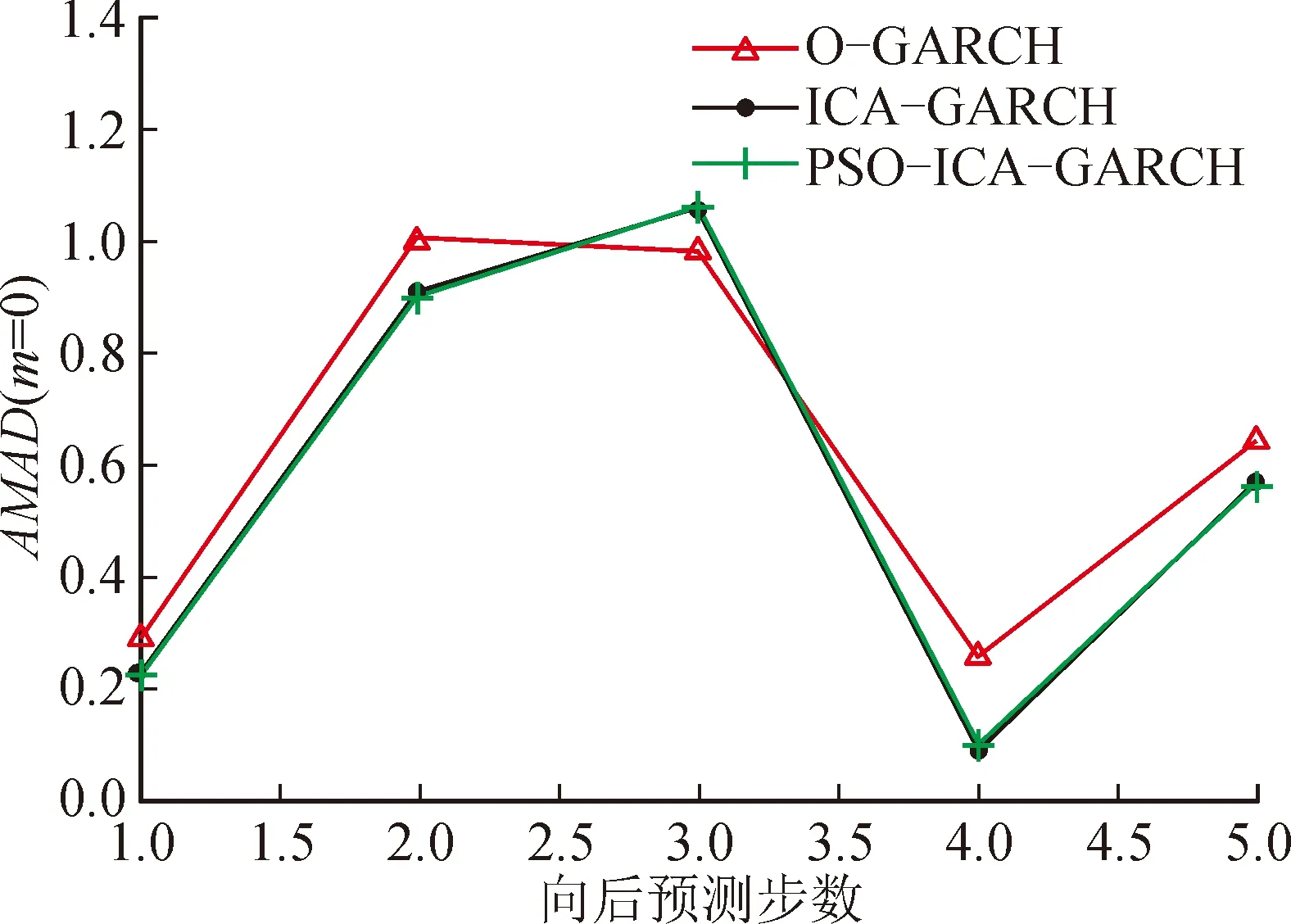
图3 O-GARCH、ICA-GARCH和PSO-ICA-GARCH模型在t分布下的预测效果Fig.3 Prediction effect of O-GARCH, ICA-GARCH and PSO-ICA-GARCH models under t distributions

从图3容易看出，ICA-GARCH和PSO-ICA-GARCH模型整体上明显比O-GARCH模型的预测偏差小，说明ICA-GARCH和PSO-ICA-GARCH模型整体上明显比O-GARCH模型的预测更准确。更进一步，从表8可以看出，除向后第3、4步PSO-ICA-GARCH和ICA-GARCH模型的预测结果相当外，向后第1、2和5步PSO-ICA-GARCH的预测偏差均明显小于ICA-GARCH 模型。综合图3和表8的分析结果，说明三种模型中，PSO-ICA-GARCH模型预测的效果最准确。

4 结 论

本文将PSO-ICA算法与GARCH模型相结合，提出了一种新的多元波动率模型，即PSO-ICA-GARCH模型，该模型能够和ICA-GARCH模型同样解决O-GARCH模型中各主成分之间弱相关，使得所做实证往往与实际情况不相符的问题，且PSO-ICA算法相较于ICA算法具有更高的分离精度，并将该模型应用到阿里巴巴概念股收益的多元波动率建模中，结果表明PSO-ICA-GARCH模型相较于O-GARCH和ICA-GARCH模型具有更好的模型预测效果,为实现更精确的多元波动率建模提供了有力的工具。